Математическое и имитационное моделирование (текст). Экономическими моделями
 Скачать 0.83 Mb.
|
|
Упражнение 5. На предприятии имеется 6 автомобилей разных моделей. Необходимо в разные районы области перевести 5 грузов. Затраты по перевозке каждого груза каждым автомобилем различны и приведены в следующей таблице
Выбрать автомобиль для каждого вида груза так, чтобы затраты на перевозку были минимальными. Определить эти затраты. Ответ.
По единицам таблицы определяем закрепление автомобилей за грузами, при этом затраты по перевозке грузов составляют 125 усл. ед. Упражнение 6. Фирма получила заказы на разработку пяти программных продуктов. Для выполнения этих заказов решено привлечь шестерых наиболее опытных программистов. Каждый из них должен написать одну программу. В следующей таблице приведены оценки времени (в днях), необходимого программистам для выполнения каждой из этих работ:
Оценки даны самими программистами, и у фирмы нет основания им не доверять. Ясно, что один из программистов не получит заказа. Распределите работы между программистами, чтобы общее количество человеко-дней, затраченное на выполнение всех пяти заказов, было минимальным. Ответ. 1- ый программист не получит заказ, 2- ой - над программой 4, 3- ий – над программой 5, 4- ый - над программой 3, 5- ый - над программой 1, 6-ой – над программой 2. Общие издержки составляют 228 тыс. руб. Элементы теории игр Основные понятия теории игр Конфликтными называются ситуации, в которых участвуют стороны, преследующие различные цели. Теория игр есть математическая теория конфликтных ситуаций. Стороны, участвующие в конфликте, называются игроками. Каждый игрок имеет некоторое множество выборов, называемых стратегиями. Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной в противном случае. Исход (результат) игры определяется функцией выигрыша, задаваемой аналитически или таблично (платежной матрицей). Игра с двумя игроками, в которой выигрыш одного из них равен проигрышу другого, называется игрой двух лиц с нулевой суммой или антагонистической. В такой игре достаточно определить результат в виде выигрыша одного из игроков. Предполагается, что функция выигрыша и множество стратегий, доступных каждому из игроков, общеизвестны. Оптимальной стратегией игрока называется такая стратегия, которая при многократном повторении игры обеспечивает одному игроку максимально возможный средний выигрыш, а другому — минимальный средний проигрыш. Задачей теории игр является определение оптимальной стратегии для каждого игрока. При этом предполагается, что лицу, принимающему решение, противостоит разумный противник. Платежная матрица Рассмотрим конечную парную игру с нулевой суммой, где у игрока А имеется m стратегий A1, A2,…,Am, а у игрока В – n стратегий B1, B2,…,Bn. В результате выбора игроками любой пары стратегий (Ai; Bj) однозначно определяется исход игры, т.е. выигрыш aij игрока А (положительный или отрицательный) и проигрыш (-aij) игрока В. Набор выигрышей aij для разных значений i, j располагают в виде матрицы, строки которой отвечают стратегиям игрока А, а столбцы – стратегиям игрока В. Такая матрица называется платежной матрицей или матрицей игры размера mn. Общий вид матрицы представлен в следующей таблице
Задать игру – это задать m стратегий игрока А, n стратегий игрока В и платежную матрицу. Пример. Пусть каждый из двух игроков А, В может записать независимо от другого цифры 1, 2, 3. Если разность между цифрами положительна, то первый игрок выигрывает количество очков, равное разности между цифрами, и, наоборот, если разность отрицательна, то выигрывает второй игрок. Если разность равна нулю, то игра заканчивается в ничью. В этой игре каждый из игроков имеет три стратегии, которые составляют матрицу игры 3×3, представляющую выигрыш игрока А. Составим платежную матрицу
В такой матричной игре целью игрока А является максимизация своего выигрыша, целью игрока В – минимизация своего проигрыша. Решение матричной игры в чистых стратегиях Для решения игры двух лиц с нулевой суммой предлагается критерий минимакса- максимина. Этот критерий основывается на выборе наилучшей из наихудших возможностей и является наиболее осторожным. Рассмотрим игру с матрицей
Каждый игрок стремится себе обеспечить максимальный выигрыш при любых действиях противника. Найдем оптимальные стратегии для каждого из игроков. Игрок А считает, что какую бы стратегию он ни выбрал, игрок В выберет стратегию, минимизирующую его выигрыш, т.е. 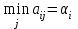 (по строкам)За оптимальную игрок А возьмет стратегию, для которой αi максимален, т.е. 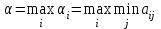 .Выбранная игроком А стратегия называется максиминной стратегией, а соответствующее ей значение выигрыша α называют нижней ценой игры. Это гарантированный выигрыш игрока А при любых стратегий игрока В В итоге, если игрок А придерживается своей максиминной стратегии, его выигрыш будет не меньше нижней цены игры, т.е. aij α. Игрок В считает, что какую бы стратегию он ни выбрал, игрок А выберет стратегию, максимизирующую его выигрыш, т.е. 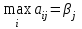 (по столбцам).За оптимальную игрок В возьмет стратегию, для которой βj минимально, т.е. 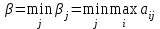 .Выбранная игроком В стратегия называется минимаксной стратегией, а соответствующее ей значение проигрыша β называют верхней ценой игры. Это гарантированный проигрыш игрока В при любых стратегий игрока А В итоге, если игрок В придерживается своей минимаксной стратегии, его проигрыш в любом случае будет не больше верхней цены игры, т.е. aij β. Из условий, определяющих критерий минимакса-максимина, следует: 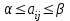 Игра, для которой α = β, называется игрой с седловой точкой. Решением игры называется пара 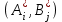 оптимальных стратегий, соответствующих седловой точке. Элемент aij = ν, соответствующий решению игры, называется ценой игры, причем ν = α = β.Решение игры обладает свойством устойчивости: если один из игроков придерживается своей оптимальной стратегии, то для другого не выгодно отклоняться от своей оптимальной стратегии. Если игра имеет седловую точку (α = β), то говорят, что она решается в чистых стратегиях. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||