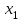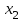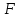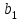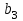Математическое и имитационное моделирование (текст). Экономическими моделями
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Свойство: Пересечение выпуклых множеств есть выпуклое множество. Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек. Полуплоскостью называется множество точек на плоскости, координаты которых удовлетворяют неравенству 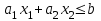 . .Уравнение 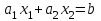 является граничной прямой полуплоскости. является граничной прямой полуплоскости.Граничная прямая делит плоскость на две полуплоскости. Для определения, на какую сторону от граничной прямой расположена данная полуплоскость, надо взять произвольную точку на плоскости, и подставить координаты этой точки в неравенство. Если неравенство справедливо, то полуплоскость обращена в сторону этой точки, иначе – в противоположную. Направление полуплоскости на рисунках штрихуется. Полуплоскости являются выпуклыми множествами. Каждое из неравенств системы ограничений определяет полуплоскость. Система ограничений в виде неравенств (пересечение) образует выпуклое множество, которое называется многоугольником решения задачи. Стороны этого многоугольника лежат на граничных прямых, а угловые точки определяются как точки пересечения смежных граничных прямых. Геометрически задача ЛП представляет отыскание такой точки многоугольника решений, координаты которого доставляют линейной функции F(x) экстремум, причем допустимыми решениями служат все точки многоугольника решений. Теорема. Если задача ЛП имеет оптимальное решение, то оно достигается в одной из угловых точек многоугольника решений. Графическое решение задач ЛП. Наиболее простым и наглядным методом ЛП является графический метод. Он применяется для решения задач ЛП с двумя переменными (на плоскости). Рассмотрим задачу об использовании ресурсов.  при ограничениях   , ,  - условие неотрицательности. - условие неотрицательности.Решим данную задачу графическим методом. ▼ Каждое неравенство системы ограничений определяет полуплоскость с граничной прямой: L1: 2x1 + 4x2 = 2000; L2: 4x1 + x2 = 1400; L3: 2x1 + x2 = 800. Условие неотрицательности определяют полуплоскости с граничными прямыми x1 = 0, x2 = 0. Для нахождения области допустимых решений (ОДР) строим граничные прямые. На плоскости прямую линию можно провести через две характерные точки, отсекаемые прямой на координатных осях. Для построения граничных прямых определим их характерные точки. L1: 2x1 + 4x2 = 2000 x1 = 0 x2 = 500, точка (0; 500); x2 = 0 x1 = 1000, точка (1000; 0). L2: 4x1 + x2 = 1400 x1 = 0 x2 = 1400, точка (0; 1400); x2 = 0 x1 = 350, точка (350; 0). L3: 2x1 + x2 = 800 x1 = 0 x2 = 800, точка (0; 800); x2 = 0 x1 = 400, точка (400; 0). Прежде чем строить на плоскости граничные прямые, введем еще ряд необходимых характеристик графического решения задач ЛП. Линией уровня функции F(x) называется множество точек (x1, x2) на плоскости, в которых функция принимает одно и то же значение, т.е. F(x)= С. Уравнение линии уровня целевой функции есть 40х1 + 60х2 = С (семейство параллельных прямых). Вектор n = (40, 60) указывает направление наибольшего возрастания целевой функции F(x) и перпендикулярен линиям уровня F(x)= С. Построим линию уровня F(x) = С, приняв С = 9600, т.е. линия уровня линия уровня определяется выражением 40х1 + 60х2 =9600. Замечание. Константа С = 9600 выбрана из условия, чтобы пересечения прямой линии уровня с координатными осями были целыми числами. Линию уровня 40х1 + 60х2 = 9600 строим по двум характерным точкам: x1 = 0 x2 = 160, точка (0; 160); x2 = 0 x1 = 400, точка (400; 0). На листе Excel заносим все характерные точки, определяющие граничные прямые и линию уровня. Используя графические средства Excel, строим все перечисленные прямые. На рис. показаны граничные прямые и ОДР (заштриховано). 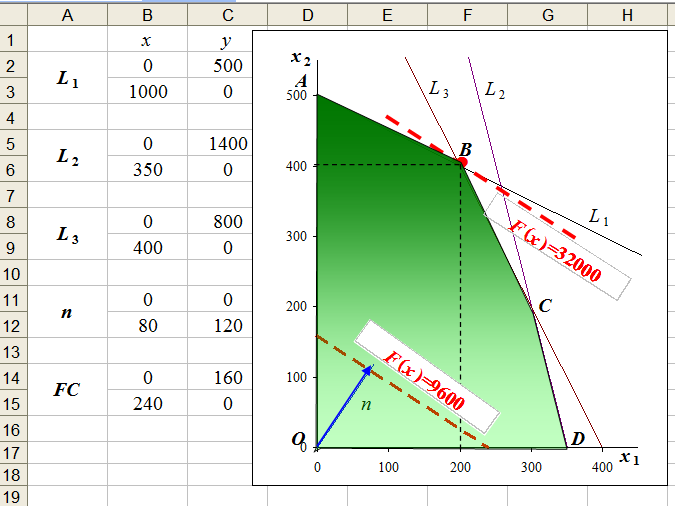 Рис. Оптимальное решение модели Среди точек этого многоугольника нужно найти такую точку, в которой линейная функция F = 40x1 + 60x2 принимает максимальное значение. Перемещая линию уровня параллельно самой себе до тех пор, пока у нее не окажется только одна общая точка с многоугольником решения (угловая точка В), получим оптимальное решение задачи ЛП, соответствующее максимальному значению целевой функции. Координаты точки В(200; 400). Таким образом, графический способ решения задачи дает оптимальное решение: 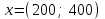 , , 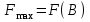 = 40·200 + 60·400 = 32000. = 40·200 + 60·400 = 32000.Это значит, чтобы получить максимальный доход в размере 32000 усл. ед., необходимо запланировать производство 200 единиц продукции Р1 и 400 единиц продукции Р2. Статус ресурсов. Ограничения линейной модели классифицируются на связывающие и не связывающие. Граничная прямая, представляющее связывающее ограничение, проходит через оптимальную точку; в противном случае ограничение является не связывающим, На рис. связывающими ограничениями являются ограничения, представленными прямыми L1, L3, а не связывающее ограничение представлено прямой L2. Статус ресурса (дефицитным или недефицитным) устанавливается в зависимости от того, полное или частичное их использование предусматривает оптимальное решение задачи. Если ограничение является связывающим, то этот ресурс относится к дефицитному (используется полностью). Если ограничение является не связывающим, то ресурс относится к недефицитному, следовательно, ресурсы 1, 3 являются дефицитными, а ресурс 2 - недефицитным. Решение задач ЛП в Excel Решение задач линейного программирования можно произвести с помощью надстройки MS Excel «Поиск решения». Надстройка становится доступной при установке MS Excel. Однако, чтобы использовать эту надстройку в Excel, необходимо сначала загрузить ее. Загрузка надстроек Поиск решения и Анализ данных: • в Microsoft Office 2010 щелкните значок Кнопка MicrosoftOffice • выберите команду Надстройки, а затем в поле Управление – пункт Надстройки Excel; • нажмите кнопку Перейти; • в окне Доступные надстройки установите флажок Поиск решения и нажмите ОК. После загрузки надстройки Поиск решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения. До вызова Поиск решения необходимо подготовить данные для решения задачи ЛП на рабочем листе Excel. Пример 3. Решим задачу ЛП. 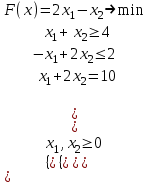 Анализ данных в Excel. Вид листа Excel для примера 3 показан в следующей таблице
Данные задачи и формулы в соответствующие ячейки вводятся следующим образом. B1:C1 — записаны обозначения переменных модели x1, x2. B2:C2 — резервируются для значений переменных модели, которые будут найдены после выполнения процедуры Поиск решения. A3:A6 — записаны обозначения строки целевой функции F и строк ограничений b1, b2, b3. B3:C3 — записаны коэффициенты при переменных модели в целевой функции. B4:C6 — заносим матрицу коэффициентов при переменных в системе ограничений модели. Е4:Е6 — записаны правые части системы ограничений модели. D3 (целевая ячейка) — вводим формулу =СУММПРОИЗВ(B3:C3;$B$2: $C$2). «Протягиваем» ее до D6 включительно. Запустить команду Поиск решения. В диалоговом окне Поиск решения выполнить: • установить целевую ячейку равной минимальному значению; • изменяя ячейки, ввести адрес переменных; • ввести ограничения; • выбрать метод решения: Поиск решения задач симплекс-методом. Заполненное диалоговое окно Поиск решения имеет вид 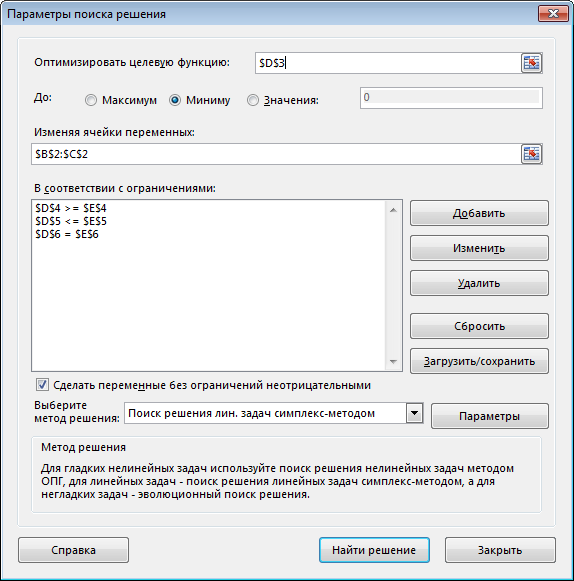 После выполнения программы работы Поиск решения получим
Оптимальное решение: x = (4; 3). Fmin (x) = 5 ▲ Пример 4 (задача составления рациона). 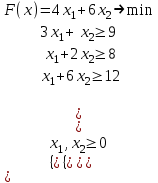 Анализ данных в Excel. Исходные данные примера 4 на рабочем листе Excel, и заполненное диалоговое окно Поиск решения имеют вид
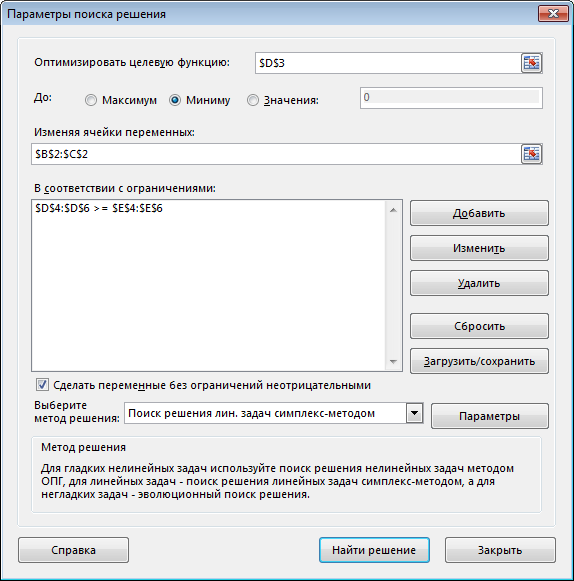 После выполнения программы работы «Поиск решения» получим
Оптимальное решение: x = (2; 3). Fmin (x) = 26 ▲ |