Математическое и имитационное моделирование (текст). Экономическими моделями
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Пример. Найдем решение игры, заданной платежной матрицей
▼ Нижняя и верхняя цена игры 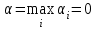 и и 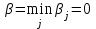 . .Поскольку α = β, то игра имеет седловую точку. Решение игры (А3, В3), цена игры ν = 0 ▲ Упражнение. Найти решение игры, заданной платежной матрицей
Ответ. Решение игры (А2, В1), цена игры ν = 4. Упражнение. Найти решение игры, заданной платежной матрицей
Ответ. Решение игры (А2, В2), цена игры ν = 0,7. Упражнение. Найти решение игры, заданной платежной матрицей
Ответ: игра не имеет седловой точки. Решение матричной игры в смешанных стратегиях Пример. Пусть игра задана платежной матрицей
Найдем решение игры. ▼ Нижняя и верхняя цена игры 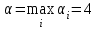 и и 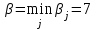 . .Поскольку α ≠ β, то игра не имеет седловой точки ▲ Если игра не имеет седловой точки (α < β), то применение чистых стратегий не дает оптимального решения игры. Поиск решения таких игр приводит к применению смешанных стратегий. Смешанными называются стратегии, состоящие в случайном чередовании чистых стратегий. Пусть x = (x1, x2,…, xm), y = (y1, y2,…, yn) наборы вероятностей, с которыми игроки А, В выбирают свои чистые стратегии, причем 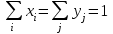 , ,где 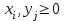 для всех i, j. для всех i, j.Платежную матрицу при смешанных стратегиях представим в виде
Основная теорема теории игр утверждает, что каждая матричная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно в области смешанных стратегий. Применение оптимальной стратегии позволяет получить выигрыш, равной цене игры ν, причем 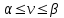 , где α, β – нижняя и верхняя цена игры. , где α, β – нижняя и верхняя цена игры.Оптимальная смешанная стратегия игрока А обеспечивает ему средний выигрыш (математическое ожидание), равный цене игры ν, если игрок В применяет свою оптимальную стратегию, или больше цены игры ν, если игрок В применяет не оптимальную стратегию. Это приводит к системе неравенств 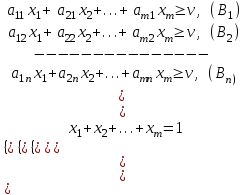 (*) (*)Левая часть каждого из неравенств представляет собой математическое ожидание выигрыша игрока А при использовании игроком В против него той или иной стратегии. Оптимальная смешанная стратегия игрока В обеспечивает ему средний проигрыш (математическое ожидание), равный цене игры ν, если игрок А применяет свою оптимальную стратегию, или меньше цены игры ν, если игрок А применяет не оптимальную стратегию. Это приводит к системе неравенств 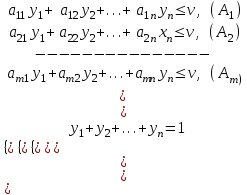 (**) (**)Левая часть каждого из неравенств представляет собой математическое ожидание проигрыша игрока В при использовании игроком А против него той или иной стратегии. Известны несколько методов нахождения оптимальных стратегий в играх двух лиц с нулевой суммой. Задача нахождения оптимального решения усложняется с ростом числа стратегий. Решение игр (m×n) с помощью ЛП Каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача ЛП и, наоборот, каждая задача ЛП может быть представлена как игра. Способ нахождения решения игры методом ЛП особенно эффективен для игр большой размерности. Оптимальная смешанная стратегия игрока А определяется условиями 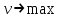 при ограничениях (*). Полученная задача ЛП может быть упрощена делением всех (n + 1) ограничений на ν. Эта операция возможна при ν > 0. В противном случае, если ν < 0, необходимо поменять знаки неравенств. Таким образом, полагая ν > 0, можем записать ограничения задачи в виде: 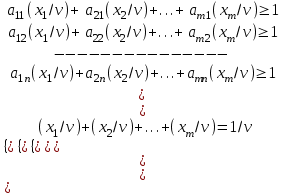 Полагая ti = (xi/v), i = 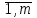 , и в силу того, что , и в силу того, что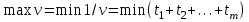 , ,запишем задачу в виде 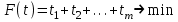 при ограничениях 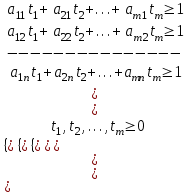 Оптимальное решение игрока А будет 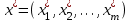 , где , где 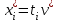 , , 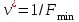 Оптимальная смешанная стратегия игрока В определяется условиями 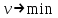 при ограничениях (**). Аналогично эта задача может быть записана как задача ЛП 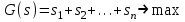 при ограничениях 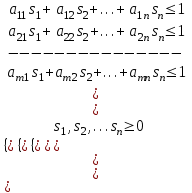 где sj = (yj/v), 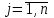 , поскольку , поскольку 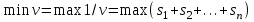 . .Оптимальное решение игрока В будет 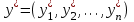 , где , где 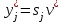 , , 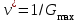 Задача игрока В является двойственной к задаче игрока А, тем самым оптимальное решение одной из задач дает оптимальное решение другой задачи. Пример 12. Найти решение игры, заданной платежной матрицей
▼ Нижняя и верхняя цена игры 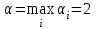 и и 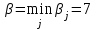 . Поскольку α ≠ β, то игра не имеет седловой точки, следовательно, решение игры в чистых стратегиях не существует. Оптимальное решение следует искать в области смешанных стратегий. . Поскольку α ≠ β, то игра не имеет седловой точки, следовательно, решение игры в чистых стратегиях не существует. Оптимальное решение следует искать в области смешанных стратегий.Пусть x1, x2, x3 – вероятности применения первым игроком стратегий А1, А2, А3, а y1, y2, y3 - вероятности использования вторым игроком стратегий В1, В2, В3. Для первого игрока математическая модель задачи имеет вид 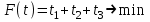 при ограничениях 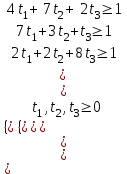 Решаем задачу в Excel (Поиск решения)
Оптимальное решение: t = (0,10584; 0,05839; 0,08394), Fmin=0,24818, тогда цена игры v* = 1/Fmin = 1/0,24818 = 4,02941, и оптимальное решение x* = tv* = (0,42647; 0,23529; 0,33824). Таким образом, первый игрок должен придерживаться стратегии х* = (0,42647; 0,23529; 0,33824), при этом получит доход не менее v* = 4,02941 усл. ед. Для второго игрока математическая модель задачи имеет вид: 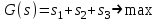 при ограничениях 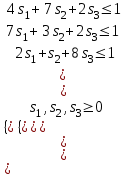 Решаем задачу в Excel (Поиск решения)
Оптимальное решение: s = (0,08759; 0,06569; 0,09489), Gmax=0,24818, тогда цена игры v* = 1/Gmax = 1/0,24818 = 4,02941, и оптимальное решение y* = sv* = (0,35294; 0,26472; 0,38235), при этом v* = 4,355 - расходы второго игрока ▲ |
