Экзаменационные вопросы Перечислите принципы управления и поясните их

• Название: Экзаменационные вопросы Перечислите принципы управления и поясните их
• Дата: 03.05.2023
• Размер: 5.35 Mb.
• Имя файла: Otvety_na_voprosy_k_ekzamenu_po_predmetu_Osnovy_teorii_upravleni.docx
• Тип: Экзаменационные вопросы; #1106767
• страница: 1 из 3

Экзаменационные вопросы

1. Перечислите принципы управления и поясните их.

Ответ :

Принято классифицировать системы автоматического управления по ряду признаков, определяющих их отношение к тому или иному классу САУ.

Прежде всего принято разделять САУ по принципу управления. По этому признаку различают системы:

• 
  с разомкнутым циклом управления,
  
• 
  с управлением по возмущениям,
  
• 
  с управлением с обратной связью,
  
• 
  с комбинированным принципом управления.
  

В системах с разомкнутым циклом управления информация о действительном поведении объекта управления не используется для целей управления (рис. 1.1).

Системы с разомкнутым принципом управления оказываются эффективными лишь тогда, когда характеристики  ОУ достаточно стабильны и возмущающее воздействие F незначительно влияет на выходную величину Y.



Рис. 1.1

В системах с управлением по возмущениям в структуру разомкнутого управления добавляется еще один блок (рис. 1.2) – устройство измерения возмущений (ИВ), обеспечивающее дополнительное компенсационное воздействие на ОУ при значительных изменениях возмущающего воздействия F.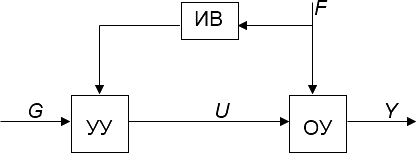



Рис. 1.2

В системах управления с обратной связью (рис. 1.3) информация о действительном поведении объекта управления снимается с выхода ОУ, обрабатывается в устройстве обратной связи (УОС) и подается в устройство сравнения (УС), где сравнивается с информацией о желаемом поведении объекта управления.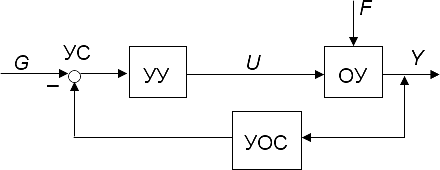



Рис. 1.3

Преимуществом систем управления с обратной связью является более высокая точность воспроизведения желаемого поведения ОУ, большая инвариантность по отношению к возмущающим воздействиям и меньшая зависимость от изменения характеристик ОУ или УУ.

В системах комбинированного управления сочетается принцип обратной связи с принципом прямого управления по внешним воздействиям: возмущающим (рис. 1.4, а) и управляющим (рис. 1.4, б).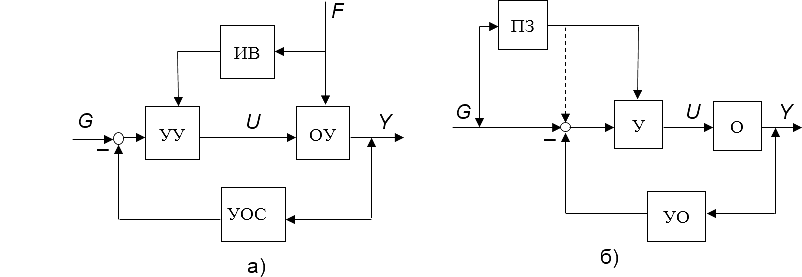



Рис. 1.4

В схеме рис. 1.4 б, ПЗ – преобразователь управляющего (задающего) воздействия. Системы с комбинированным принципом управления обеспечивают повышенную точность воспроизведения желаемого в технике управления.

2. Что представляет собой закон управления?

Ответ:

Законы управления. Типовые регуляторы

Закон управления - это алгоритм или функциональная зависимость, в соответствии с которыми регулятор формирует управляющее воздействие u(t). Эта зависимость может быть представлена в виде

u(t) = F(x, g, f), (8.1)

где F - некоторый оператор от отклонения x, задающего воздействия g и возмущающего воздействия f, а также от их производных и интегралов по времени.

Обычно выражение (8.1) может быть записано следующим образом:

u(t) = F₁(x) + F₂(g) + F₃(f). (8.2)

Здесь первое слагаемое соответствует управлению по отклонению, второе и третье - управлению по внешнему воздействию.

В зависимости от вида оператора F законы управления делятся на стандартные и специальные.

Стандартные законы управления - это универсальные законы, с помощью которых можно решать задачи автоматизации разнообразных технологических процессов и объектов.

Специальные законы управления - это законы, формируемые для решения конкретных задач.

Если для формирования управляющего воздействия u(t) используются только линейные математические операции, то такой закон управления называется линейным, в противном случае - нелинейным.

Линейный стандартный закон управления имеет следующий вид: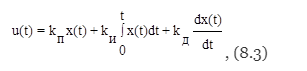



где первое слагаемое является пропорциональной, второе - интегральной, третье - дифференциальной составляющими закона, а коэффициенты k_П, k_И и k_Д определяют вклад каждой из составляющих в формируемое управляющее воздействие.

Интегральная составляющая закона управления вводится для повышения точности, а дифференциальная - для повышения быстродействия работы системы.

Регулятор, формирующий управляющее воздействие в соответствии с (8.3), имеет передаточную функцию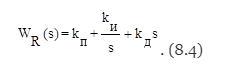



Структурная схема линейного стандартного регулятора приведена на рис.8.1.

Настройка такого регулятора заключается в задании значений коэффициентов k_П, k_И, k_Д таким образом, чтобы удовлетворить требованиям качества управления в соответствии с выбранными критериями качества.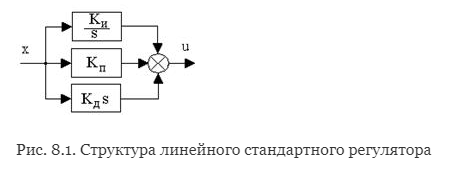



На практике широкое распространение получили типовые или промышленные регуляторы, представляющие собой универсальные автоматические устройства, легко приспосабливаемые для автоматизации разнообразных технологических процессов и объектов. При этом объект управления, как правило, является звеном статического типа, т.е. W_ОУ(0)=k_ОУ, где k_ОУ - коэффициент передачи объекта управления. Типовые регуляторы реализуют типовые законы управления, являющиеся частными случаями линейного стандартного закона управления, и классифицируются следующим образом.

П-регуляторы. Реализуют П-закон или пропорциональный закон управления

u(t) = k_П x(t).

Передаточная функция П-регулятора

W_R(s) = k_П.

Пропорциональное управление позволяет уменьшить установившуюся ошибку в объекте в (1+k) раз, где k = k_П´k_ОУ - коэффициент передачи разомкнутой системы. Регулирование в этом случае получается статическим, так как при любом конечном значении коэффициента передачи разомкнутой системы установившаяся ошибка будет отличной от нуля.



При интегральном управлении получается система, астатическая по отношению к задающему воздействию. Повышение степени астатизма приводит к увеличению установившейся точности системы, но одновременно снижает ее быстродействие, а также приводит к ухудшению устойчивости. Снижение быстродействия объясняется тем, что в первый момент времени при появлении ошибки управляющее воздействие равняется нулю и только затем начинается его рост. В системе пропорционального управления рост управляющего воздействия в первые моменты времени происходит более интенсивно, так как наличие ошибки сразу дает появление управляющего воздействия, в то время как в системе интегрального управления должно пройти некоторое время.



Пропорционально-интегральное (изодромное) управление сочетает в себе высокую точность интегрального управления (астатизм) с большим быстродействием пропорционального управления. В первые моменты времени при появлении ошибки система с ПИ-регулятором работает как система пропорционального регулирования, а в дальнейшем начинает работать как система интегрального управления.



Пропорционально-дифференциальное управление применяются для повышения быстродействия работы системы.

Регулирование по производной не имеет самостоятельного значения, так как в установившемся состоянии производная от ошибки равна нулю и управление прекращается. Однако она играет большую роль в переходных процессах, потому что позволяет учитывать тенденцию к росту или уменьшению ошибки. В результате увеличивается скорость реакции системы, повышается быстродействие, снижается ошибка в динамике.

ПИД-регуляторы. Реализуют ПИД-закон или пропорционально-интегрально-дифференциальный закон управления, соответствующий линейному стандартному закону вида (8.3).

ПИД-регулятор, представляющий собой астатический изодромный регулятор с предвидением, обеспечивает повышенную точность и повышенное быстродействие системы.

3. Каково назначение регулятора в системе?

Ответ:

Регулятор, или управляющее устройство, — в теории автоматического управления это устройство, которое следит за состоянием объекта управления как системы и вырабатывает для неё управляющие сигналы. Регулятор следит за изменением некоторых параметров объекта управления (непосредственно либо с помощью наблюдателей) и реагируют на их изменение с помощью некоторых воздействий в соответствии с заданным качеством управления. Регуляторы в подавляющем большинстве работают по принципу отрицательной обратной связи с целью компенсировать внешние возмущения, действующие на объект управления, и отработать заданный извне или заложенный в системе закон управления.  Основным назначением регулятора является компенсация основных инерционностей контура;

4. По каким признакам классифицируются системы управления?

Ответ:

1)  Прежде всего принято разделять САУ по принципу управления. По этому признаку различают системы:

• 
  с разомкнутым циклом управления,
  
• 
  с управлением по возмущениям,
  
• 
  с управлением с обратной связью,
  
• 
  с комбинированным принципом управления.
  

2) Вторым важным признаком классификации САУ является тип управления. По типу управления различают шесть основных классов систем управления:

• 
  системы стабилизации;
  
• 
  системы  программного управления;
  
• 
  следящие системы;
  
• 
  системы оптимального управления;
  
• 
  системы экстремального управления;
  
• 
  системы адаптивного управления.
  

3) Третьим существенным признаком классификации САУ  является характер сигналов управления, используемых в системах управления. По этому признаку все системы разделяются на:

• 
  непрерывные
  
• 
  релейные,
  
• 
  дискретные.
  

Дискретной системой называется такая САУ, в которой имеет место прерывистый характер передачи информации управления. Такой характер сигналов управления  может быть обусловлен включением в систему импульсных или цифровых устройств. В связи с этими  все дискретные системы разделяются на две большие группы:

• 
  импульсные САУ;
  
• 
  цифровые САУ.
  

5. Дайте классификацию систем по виду задающего воздействия.

Ответ:

По виду задающего воздействия замкнутые САУ бывают системами следящими, стабилизации и программного управления.

Следящей называется САУ, предназначенная для воспроизведения произвольного задающего воздействия g(t), например, следящая система дистанционного управления орудием.

Если функция g(t) - заранее известная функция времени (заданная программа изменения температуры в термокамере), то соответствующая следящая система называется системой программного управления.

Если функция g(t) = const, то такая следящая система называется системой стабилизации

6. Назовите необходимые и достаточные условия линейности систем.

Ответ:

Линейные системы - это системы, которые описываются линейными уравнениями (алгебраическими и дифференциальными или разностными). Если система описывается обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами, то систему называют обыкновенной линейной системой. Закон управления линейной системы формируется линейными математическими операциями.

Необходимые и достаточные условия линейности системы:

1) в установившемся процессе выходной сигнал должен в некотором масштабе повторять входной сигнал;

2) сумме двух входных воздействий должна соответствовать сумма соответствующих выходных переменных.

К линейным системам применим принцип суперпозиции, в соответствии с которым выходной сигнал линейной системы на любое произвольное входное воздействие можно определить через ее реакцию на определенное элементарное воздействие.

7. Что представляет собой система управления?

Ответ:

Система управления представляет собой совокупность объекта управления, регулятора и датчика рассогласования. Типовая автоматическая система может быть представлена в следующем виде (рис.1.6).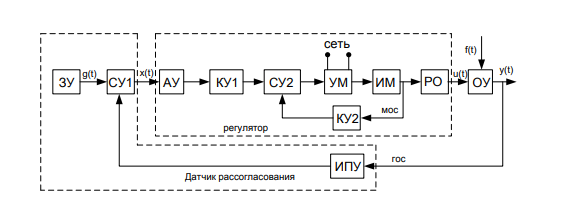



Рис. 1.6. Функциональная схема типовой автоматической системы

Координаты (переменные) системы:

g(t) –задающее воздействие;

y(t) – управляемая величина;

f(t) – возмущающее воздействие;

x(t) = g(t) - y(t) – рассогласование;

u(t) – управляющее воздействие.

8. Перечислите основные элементы системы автоматического управления

Ответ:

Функциональные элементы системы:

ОУ – объект управления;

ЗУ – задающее устройство;

ИПУ – измерительно-преобразовательное устройство;

СУ1, СУ2 – сравнивающие устройства;

РО – регулирующий орган, представляет собой техническое

устройство, которое действует на объект управления и непосредственно изменяет управляемую величину y(t);

ИМ – исполнительный механизм, представляет собой техническое устройство, воздействующее на регулирующий орган;

УМ – усилитель мощности, представляет собой техническое устройство, которое питает энергией исполнительный механизм;

АУ – амплитудный усилитель, устройство, обеспечивающее требуемую чувствительность системы и, в конечном счете, точность ее работы;

КУ1, КУ2 – корректирующие устройства, включаются в систему для того, чтобы сформировать требуемый закон управления для реализации заданного качества управления;

ГОС – главная обратная связь, реализуется измерительнопреобра-зовательным устройством и обеспечивает передачу информации об управляемой величине на вход системы;

МОС – местная или внутренняя обратная связь.

В настоящее время для управления широко используется вычислительная техника, которая позволяет программно реализовать задающее устройство, амплитудный усилитель, сравнивающие и корректирующие устройства. Остальные функциональные элементы реализуются аппаратно.

ЗУ, ИПУ и СУ1 образуют датчик рассогласования ДР.

Все остальные функциональные элементы за исключением объекта управления составляют регулятор R. Регулятор, в котором датчик рассогласования может непосредственно (без дополнительного источника энергии) воздействовать на регулирующий орган, называется регулятором прямого действия.

Таким образом, любую систему управления, рассматриваемую как совокупность объекта управления ОУ, датчика рассогласования ДР и регулятора R, можно изобразить в виде упрощенной функциональной схемы (рис. 1.7).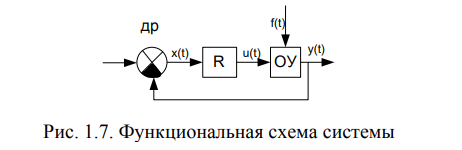



Элементы системы:

ОУ – объект управления;

ДР - датчик рассогласования;

R – регулятор.

Координаты (переменные) системы:

g(t) – задающее воздействие;

y(t) – управляемая (регулируемая) величина;

f(t) – возмущающее воздействие;

x(t) - рассогласование (ошибка);

u(t) – управляющее воздействие.

Еще в более общем виде систему управления можно рассматривать как ”черный ящик” (рис. 1.8), преобразующий задающее воздействие в управляемую величину.



9. Каково назначение математического описания систем?

Ответ :

Целью математического описания САУ является составление математической модели, используемой для анализа и синтеза САУ. Любая математическая модель является, приближением к действительному состоянию взаимодействия отдельных информационных параметров объекта или всей системы в целом и отражает наиболее существенные взаимосвязи между переменными величинами.

Различают следующие виды математических моделей САУ:

1. дифференциальные и разностные уравнения систем управления и их элементов;

2. векторно-матричные модели в пространстве состояний;

3. передаточные функции элементов и систем управления;

4. структурные схемы систем управления;

5. направленные графы систем управления;

6. временные характеристики САУ;

7. частотные характеристики САУ.

Эти же виды математических моделей используются и для описания нелинейных САУ.

10. Что такое динамика системы?

Ответ:

Для анализа и синтеза системы управления требуется ее математическое описание, которое бы связывало поведение координат системы - ее переменных величин в процессе работы, то есть во времени. Поведение координат системы во времени называется динамикой системы. Так как система состоит из взаимосвязанных функциональных элементов, то для получения ее математического описания необходимо получить математические описания отдельных элементов. Математическое описание элемента устанавливает связь во времени между его текущими значениями выходных y(t) и входных x(t) величин. Динамика элемента, то есть поведение его координат во времени, описывается дифференциальными уравнениями. В динамике связь между координатами, то есть между входными и выходными величинами, меняется во времени. Динамика характеризуется переходным процессом. При времени, стремящемся к бесконечности t, текущие координаты y(t) и x(t) принимают постоянные установившиеся значения и наступает статика элемента, которая описывается алгебраическими уравнениями. В статике входные и выходные величины элемента постоянные: x()=x0=const; y()=y0=const. Эти постоянные величины называются установившимися. А процесс, соответствующий статике, называется установившимся процессом. Теоретически статика наступает при t, однако на практике принято считать, что статика наступает тогда, когда текущие координаты отличаются от своих установившихся значений не более чем на 5%. Динамическое уравнение отдельного элемента составляется по правилам соответствующей технической науки (элемент может пред- 21 ставлять собой электрическую машину, механическую передачу, нагревательный прибор, электрическую цепь, электронную схему и т.п.).

11. Как перейти от дифференциального уравнения к операторному?

Ответ:

Чтобы произвести расчет САУ, надо иметь математическую модель системы. Обычно математической моделью является дифференциальное уравнение, которое получают, анализируя физический, механический или иной процесс.

Операторное уравнение получают, применяя преобразование Лапласа к дифференциальному уравнению.

Суть преобразования Лапласа в том, что функцию от времени

преобразуют в функцию от комплексного временного

( −действительная часть, − мнимая часть, j = 1).

Функцию от времени называют «оригинал», а ее преобразование по Лапласу – «изображение».

Для изображения используют прописные буквы.

Символически преобразование Лапласа принято обозначать прописной буквой L. Например,

L= {x(t)}= X( p), L{y(t)}=Y( p), L{ f (t)}= F( p).

12. Дайте определение передаточной функции.

Ответ:

Передаточная функция – одна из основных динамических характеристик объекта

регулирования.

Передаточной функцией объекта W(p) называется отношение преобразованного по

Лапласу выхода объекта у(р) к преобразованному по Лапласу входу x(р).

Передаточная функция является функцией комплексного переменного.



13. Как по дифференциальному уравнению звена найти его передаточную функцию?

Ответ:



14. Что такое динамическое звено и его характеристика?

Ответ:

Динамическим звеном называют устройство любого физического типа и конструктивного оформления, которое описывается определённым дифференциальным уравнением.

Согласно определению динамические звенья классифицируются по типу дифференциальных уравнений или по их порядку. То есть устройства разных типов могут быть описаны одинаковыми дифференциальными уравнениями. Основными параметрами динамических звеньев являются постоянные коэффициенты дифференциальных уравнений. Буквой Т обозначается постоянная времени , а буквой k коэффициент передачи. Соединяться динамические звенья могут 3 способами: Последовательно, параллельно и в виде обратной связи.

15. Дайте определение основных характеристик.

Ответ:







































16. Какие частотные характеристики используются для исследования систем?

Ответ:

Для исследования систем используются: Частотная передаточная функция (ЧПХ), Амплитудно-фазовая частотная характеристика (АФЧХ), Амплитудная частотная характеристика (АЧХ), Фазовая частотная характеристика (ФЧХ), Вещественная частотная характеристика (ВЧХ), Мнимая частотная характеристика (МЧХ), Логарифмические частотные характеристики (ЛЧХ), логарифмической амплитудной частотной характеристики (ЛАХ) и логарифмической фазовой частотной характеристики (ЛФХ).

17. Почему ЛЧХ нашли большое применение в инженерной практике?

Ответ:

Метод исследования устойчивости с помощью логарифмических частотных характеристик получил широкое распространение в инженерной практике. Это обусловлено тем, что построение логарифмических частотных характеристик значительно проще, чем построение годографа амплитудно-фазовых характеристик.

18. По каким признакам классифицируются типовые динамические звенья?

Ответ:

Динамическим звеном называют устройство любого физического вида и конструктивного оформления, представленное определенным дифференциальным уравнением.

Типовым называется такое звено, которое описывается дифференциальным уравнением не выше второго порядка.

В соответствии с определением классификация динамических звеньев производится по виду дифференциального уравнения, а именно, по его порядку. Так как одними и теми же дифференциальными уравнениями могут описываться устройства любого типа (электрические, электромеханические, гидравлические, тепловые), то такое предположение позволяет использовать для проектирования различных устройств одинаковые подходы.

19. Перечислите группы основных типов звеньев.

Ответ:

Любую систему можно представить в виде соединения типовых динамических звеньев. Число таких звеньев невелико и определяется типом нулей и полюсов.

Типовым называется такое звено, которое описывается дифференциальным уравнением не выше второго порядка. К таким звеньям относятся:

• 
  безынерционное звено – звено нулевого порядка,
  
• 
  апериодическое звено – звено первого порядка,
  
• 
  интегрирующее звено – звено первого порядка,
  

• 
  дифференциальное звено – звено первого порядка,
  
• 
  колебательное звено – звено второго порядка.
  
• 
  
  

1. Уравнение движения для безинерционного звена имеет вид

2. Уравнение движения для апериодического звена имеет вид

3. Уравнение движения для интегрирующего звена имеет вид

4. Уравнение движения для дифференцирующего звена имеет вид

5. Уравнение движения для колебательного звена имеет вид

20. Что представляет собой структурная схема системы управления?

Ответ :

Структурной схемой САУ называется графическая форма представления математической модели системы в виде соединения отдельных звеньев, каждое из которых задано каким-либо математическим оператором преобразования входного сигнала в выходной. Операторы преобразования могут быть заданы символами преобразования во временной области или в области изображений (передаточные функции) или с помощью статических и динамических характеристик. Звенья представляются на структурных схемах с помощью прямоугольников. Соединение их осуществляется стрелками, указывающими направления передачи сигналов управления. Прохождение сигналов управления против направления, указанного стрелками, невозможно. Различные варианты представления звеньев структурной схемы показаны на рис. 2.2.



Отметим, что звенья, выполняющие математические операции «умножение» и «деление», изображаются также прямоугольниками. Звенья же, выполняющие алгебраические операции «сложение» и «вычитание», изображаются кружками с подходящими отходящими стрелками. Причем, отсутствие у подходящих стрелок каких-либо математических знаков означает суммирование сигналов. Присутствие знаков у стрелки означает, что этот сигнал вычитается из сигнала, соответствующего другой стрелке.

21. Какие способы соединений звеньев используются в системах

Ответ:







 характеризуется тем, что выходной сигнал звена подается на его вход.

22. Дайте определение устойчивости системы с физической и математической точек зрения

Ответ: