Экзаменационные вопросы Перечислите принципы управления и поясните их
 Скачать 5.35 Mb. Скачать 5.35 Mb.
|
|
Физическое определение устойчивости системы – это свойство системы возвращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему из этого состояния. Неустойчивая система не возвращается в исходное состояние, а непрерывно удаляется от него. Неустойчивость систем автоматического управления возникает из-за: 1) неправильного действия обратной связи; 2) очень сильного действия обратной связи. Математическое определение устойчивости системы – система является устойчивой, если свободная составляющая хС(t) переходного процесса с течением времени стремится к нулю, т.е. если 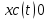 . Это условие асимптотической устойчивости. . Это условие асимптотической устойчивости.Если свободная составляющая неограниченно возрастает, т.е. если , 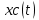 то система неустойчива. то система неустойчива.Если хС(t) не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости. 23. Какой характер имеет переходный процесс в устойчивой и неустойчивой системах? Ответ:   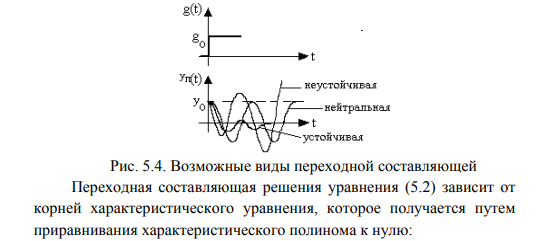     24. Сформулируйте необходимое условие устойчивости. Ответ: Необходимым, но недостаточным условием устойчивости системы является положительность (отрицательность) всех коэффициентов характеристического уравнения системы т.е. соблюдение условия 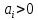 для всех i от 0 до n, где n - порядок системы. для всех i от 0 до n, где n - порядок системы.25. Что такое граница устойчивости? Каким образом при этом расположены корни характеристического уравнения системы на плоскости комплексного переменного? Ответ: Если корни характеристического уравнения расположены на мнимой оси, то система находится на границе устойчивости. При этом возможны два случая: корень в начале координат и пара мнимых корней. Нулевой корень появляется, когда свободный член характеристического уравнения равен нулю. В этом случае границу устойчивости называют апериодической. Если остальные корни этого уравнения имеют отрицательные вещественные части, то система устойчива не относительно выходного сигнала, а относительно его производной, выходной сигнал в установившемся режиме имеет произвольное значение. Такие системы называют нейтрально устойчивыми. В том случае, когда характеристическое уравнение имеет пару мнимых корней, границу устойчивости называют колебательной. 26. Сформулируйте критерий устойчивости Гурвица. Ответ :  Главные определители матрицы Гурвица имеют вид  Сам критерий формируется следующим образом: Для устойчивости замкнутой системы необходимо и достаточно, чтобы при a0 > 0 были положительными n главных диагональных определителя матрицы Гурвица. 27. Каким образом по критерию Гурвица определяются границы устойчивости? Ответ:  28. Сформулируйте критерий устойчивости Найквиста. Ответ:       29. Что такое запасы устойчивости? Каким образом они определяются по АФЧХ разомкнутой системы? Ответ: Запасы устойчивости и методы их определения Поскольку параметры системы в процессе работы могут изменять свою величину, то система, устойчивая при одних значениях параметров, может стать неустойчивой при их изменении. Таким образом, важное значение приобретает количественная оценка, характеризующая степень удаленности системы от неустойчивого состояния, называемая запасом устойчивости. Замкнутая система может перейти в состояние самовозбуждения (генерации) при одновременном выполнении двух условий: | K(jco) | = 1 (баланс амплитуд) и (р{оз) = -л (баланс фаз). Если хотя бы одно из этих условий не выполняется, система будет устойчива. Запасы устойчивости определяют на двух частотах: частоте среза (<ус), на которой модуль коэффициента передачи равен 1, и критической частоте (й^,), на которой фазовый сдвиг составляет -л. Различают запас устойчивости по модулю (по усилению) и по фазе. Запас устойчивости по фазе (ЗУФ) определяют как величину угла Д(р= л-1 i//((oc) | для частоты сос, при которой | K(jo)c) | >1. Таким образом, он по казывает, на сколько градусов не выполняется баланс фаз при выполнении баланса амплитуд. Запас устойчивости по модулю (ЗУМ) показывает, во сколько раз модуль коэффициента передачи на критической частоте (при (р(сокр) = -я) отличается от 1: і 1 h Запасы устойчивости могут быть определены как по годографу К(]со), так и по логарифмическим частотным характеристикам Цсо) и (р{со). На рисунке 10.9 показан пример определения запасов устойчивости по годографа K(ja>  Если годограф пересекает вещественную ось только справа от точки (- 1), то системы РА называют абсолютно устойчивыми, как показано на рисунке 10.10. С ростом коэффициента передачи модуль АФЧХ также растет. При некотором значении к = ккр, называемом критическим коэффициентом усиления, АФЧХ пройдет через точку (-1), то есть система будет на границе устойчивости. При к > ккр система будет неустойчива. Таким образом, увеличение коэффициента передачи по петле обратной связи снижает устойчивость. Недостатком определения запасов устойчивости по годографу является сложность построения амплитудно-фазовой характеристики. Значительно проще провести анализ устойчивости по логарифмическим частотным характеристикам. 30. Как определяются запасы устойчивости по ЛЧХ? Ответ:   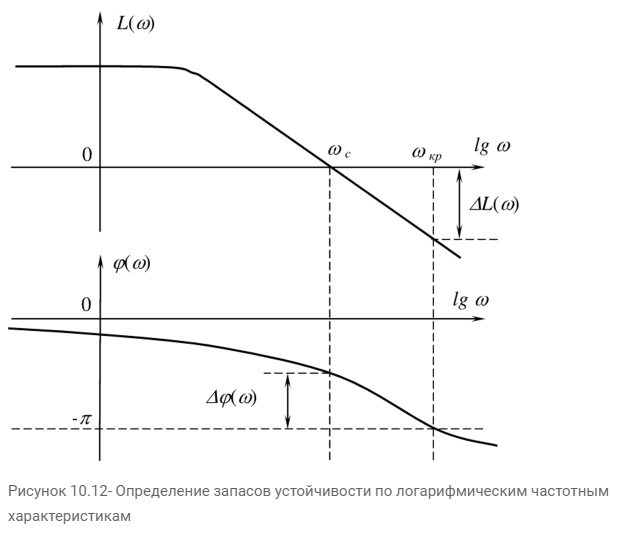 Таким образом: 1. Критерий устойчивости Найквиста основан на анализе комплексного коэффициента передачи разомкнутой системы K(j(o), при этом анализируется поведение вектора K(jco) на комплексной плоскости - годограф Найквиста, который может быть получен как теоретически, так и экспериментально. 2. Для устойчивых замкнутых систем годограф Найквиста не должен охватывать точку (-1) на действительной оси, либо охватывать её т/2 раз в положительном направлении (против часовой стрелки), где т - число корней с положительной вещественной частью в характеристическом уравнении разомкнутой системы. 3. Упростить анализ устойчивости замкнутой системы для случая, когда разомкнутая система неустойчива, позволяет правило переходов. 4. Критерий Найквиста позволяет определить запасы устойчивости (количественная оценка степени удаленности системы от неустойчивого состояния). При этом различают запасы устойчивости по модулю и по фазе, которые можно определить как по АФЧХ, так и по логарифмическим частотным характеристикам. 31. Дайте понятие качества работы системы управления. Чем оно определяется? Ответ: Общие понятия Качество работы представляет собой комплексную оценку работы системы управления, включающую устойчивость, точность, быстродействие и зависящую от назначения системы. Устойчивость системы обеспечивает затухание переходных процессов с течением времени, т.е. обеспечивает принципиальную возможность прихода системы в некоторое установившееся состояние при любом внешнем воздействии. Однако далее требуется, вопервых, чтобы это установившееся состояние было достаточно близко к заданному и, во-вторых, чтобы затухание переходного процесса было достаточно быстрым, а отклонения при этом были бы невелики. Качество работы любой системы управления в конечном счете определяется величиной ошибки, равной разности между требуемым и действительным значениями управляемой величины: x(t)=g(t)y(t) 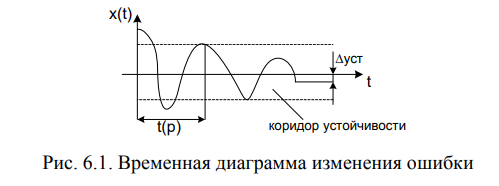     32. Как производится оценка точности работы систем? Ответ:              33. Чему равны первые два коэффициента ошибок в системах с астатизмом первого и второго порядков? Ответ:             34. Определите показатели качества переходного процесса и частотные показатели, поясните их физический смысл. Ответ:          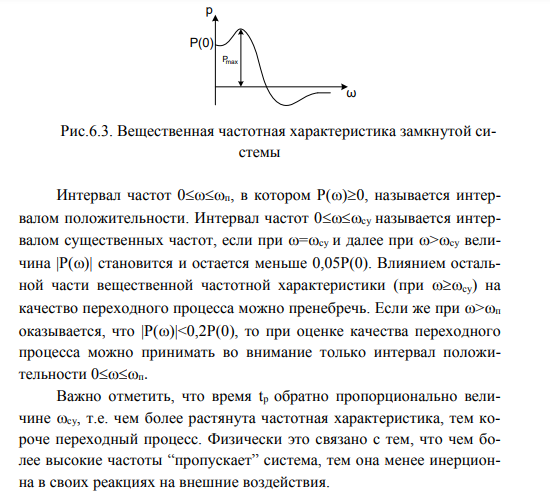  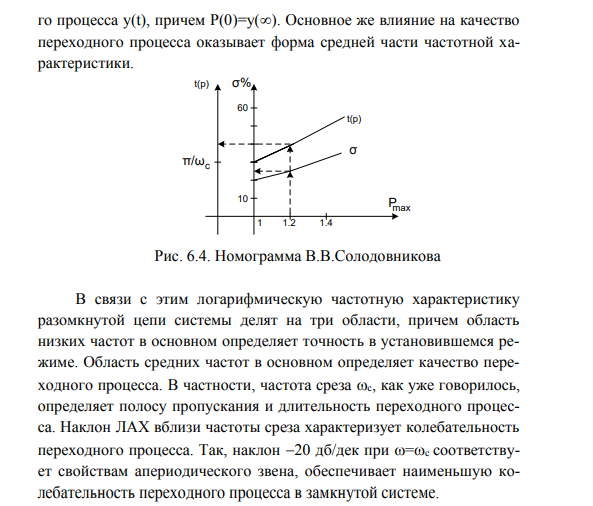  35. Что представляют собой корневые оценки качества? Ответ: Корневые оценки качества Корневые критерии качества основываются на исследовании расположения корней характеристического уравнения замкнутой системы, то есть полюсов передаточной функции системы, а также и нулей этой передаточной функции. Вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического управления. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая ограничения на корни характеристического уравнения. Для оценки быстродействия системы используется понятие степени устойчивости, являющейся простейшей корневой оценкой качества. Под степенью устойчивости a понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис.6.5). Если ближайшим является вещественный корень, то такая степень устойчивости называется апериодической, так как ей соответствует апериодическая составляющая переходного процесса с1e-at. Время ее затухания характеризует общую длительность переходного процесса, так как все члены решения, соответствующие остальным корням, затухают быстрее, т.е.  Если ближайшем к мнимой оси окажется пара комплексных корней, то ей соответствует колебательная составляющая переходного процесса с1e-atsin(bt+b1), при этом оценка длительности переходного процесса остается прежней. Такая степень устойчивости называется колебательной. Для оценки запаса устойчивости системы введено понятие колебательности переходного процесса. Колебательность определяется величиной  где a и b - вещественная и мнимая части корней характеристического уравнения. Именно эта величина характеризует быстроту затухания колебаний за каждый период T=2p/b. Чем выше колебательность, тем слабее затухание колебаний в переходном процессе. Суммарное требование определенных значений степени устойчивости a и колебательности m приводит к области, изображенной на рис.6.6, внутри которой должны располагаться все корни характеристического уравнения замкнутой системы. Далее необходимо иметь в виду, что для определения качества переходного процесса при единичном скачке задающего воздействия существенны не только корни характеристического уравнения, т.е. полюса, но также и нули передаточной функции замкнутой системы.  Для уменьшения амплитуд отклонений выходной величины системы в переходном процессе желательно, чтобы нули передаточной функции замкнутой системы располагались вблизи ее полюсов. Примером корневых оценок качества переходного процесса в системах третьего порядка является диаграмма Вышнеградского (дана в его работе 1876 г., положившей начало развития теории управления) [1,2]. Задание области расположения полюсов и нулей позволяет более полно оценить вид переходного процесса. При выборе расположения полюсов и нулей передаточной функции необходимо придерживаться общих рекомендаций [1]. 1. Желательно располагать нули вблизи области расположения полюсов. Удаление нулей от полюсов ведет к увеличению амплитуд собственных колебаний в переходном процессе. 2. Для уменьшения отклонений в переходном процессе выгодно удалять полюсы друг от друга. 3. Приближение друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси. Кроме этих рекомендаций сохраняют свою силу ограничения на область расположения полюсов, накладываемые в связи с требованием обеспечения определенного запаса устойчивости и быстродействия. 36. В чем удобство и недостатки интегральных критериев качества? Ответ: |
