Экзаменационный билет 1
 Скачать 3.38 Mb.
|
|
Вывод уравнения для скорости осаждения частиц в гравитационном поле. Условия соблюдения закона Стокса. Седиментационный анализ, расчет и назначение кривых распределения частиц по размерам. Характерным общим свойством суспензий, порошков, эмульсий и аэрозолей, особенно если они разбавлены, является склонность к оседанию или всплыванию частиц дисперсной фазы. Оседание частиц дисперсной фазы называется седиментацией, а всплывание частиц — обратной седиментацией. На каждую частицу в системе действует сила тяжести (гравитационная сила) и подъемная сила Архимеда:  Эти силы постоянны и направлены в разные стороны, равнодействующая сила, вызывающая седиментацию, равна:  Так как седиментация протекает в определенной среде, то при ламинарном движении частицы возникает сопротивление — сила трения, пропорциональная скорости движения частицы:  Таким образом, сила, действующая на частицу, во время движения, равна:  C ростом скорости при достаточно большом коэффициенте трения наступает момент, когда сила трения достигает силы, вызывающей седиментацию, и таким образом движущая сила F оказывается равной нулю.  Выражение для силы трения, возникающей при движении сферических частиц, можно представить в виде закона Стокса:  .Подставляя ее в полученное уравнение и выражая объем частицы через ее радиус, получим:  1) Закон Стокса справедлив, если частицы дисперсной фазы осаждаются независимо друг от друга, что может быть только в разбавленных системах. 2) Обычно частицы в дисперсных системах и твердой дисперсной фазой имеют неправильную форму. При свободном оседании частица несферической формы ориентируется в направлении движения таким образом, чтобы создавалось максимальное сопротивление движению, что уменьшает скорость осаждения. 3) Закон Стокса может не соблюдаться и при турбулентном режиме осаждения частиц. 4) Закон Стокса предполагает наличие внутреннего трения, или вязкого трения, когда граница (поверхность) движения частицы относительно среды находится внутри дисперсионной среды, вязкость которой определяет коэффициент трения. Если межфазное взаимодействие мало, граница (поверхность) движения частицы относительно среды может совпадать с поверхностью раздела фаз и трение оказывается внешним. Это приводит к возникновению скольжения, ускоряющему движение частицы. 5) Применимость закона Стокса ограничивается также дисперсностью частиц. Большие частицы (>100 мкм) могут двигаться ускоренно, очень малые частицы — ультрамикрпгетерогенные (<0,1 мкм) осаждаются настолько медленно, что следить за такой седиментацией практически невозможно. Принцип седиментационного метода анализа дисперсности состоит в измерении скорости осаждения частиц, обычно в жидкой среде. По скорости осаждения с помощью соответствующих уравнений рассчитывают размеры частиц. Метод позволяет определить распределение частиц по размерам и соответственно подсчитать их удельную поверхность. П 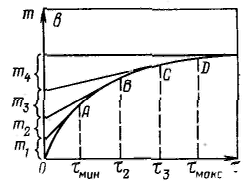 ри седиментационном анализе дисперсности полидисперсных систем определяют время осаждения частиц отдельных фракций, рассчитывают скорости их осаждения и соответствующие им размеры частиц. Для этого сначала измеряют зависимость массы осевшего осадка от времени, строят график этой зависимости, называемой кривой седиментации, по которому затем определяют все необходимые характеристики дисперсной системы.Имеются графические и аналитические методы расчета кривой седиментации. Р 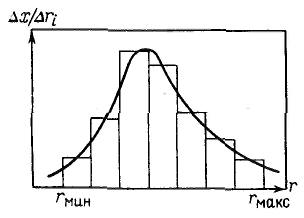 еальная кривая седиментации полидисперсной системы обычно получается плавной и ей отвечает множество бесконечно малых участков, касательные в каждой точке этой кривой отражают седиментацию данной бесконечно малой фракции.Результаты седиментациоиного анализа дисперсности полиднсперсных систем представляют также в виде кривых распределения частиц по размерам, характеризующих степень полиднсперсности системы. Кривая распределения является наглядной и удобной характеристикой полидисперсности системы, по которой легко определить содержание различных фракций. Ее строят подобно кривой распределения пор по размерам. Обычно сначала получают интегральную кривую распределения, проводят ее выравнивание с учетом точности получаемых средних значений радиусов частиц фракций и затем по ней строят дифференциальную кривую распределения. Иногда дифференциальную кривую строят сразу. На оси абсцисс откладывают значения радиусов; на ось ординат наносят отношение приращения массовых долей к разности радиусов частиц соседних фракций Δx/Δri. Построив на графике отдельные прямоугольники для каждой фракции (гистограмму) и соединив плавной кривой середины их верхних сторон, получают дифференциальную кривую распределения частиц полидисперсной системы по размерам.
 Экзаменационный билет № 6
Термодинамическая реакционная способность характеризует способность вещества переходить в какое-либо иное состояние, например, переходить в другую фазу, вступать в химическую реакцию. Она указывает на удаленность данного состояния вещества или системы компонентов от равновесного состояния при определенных условиях. Термодинамическая реакционная способность определяется химическим сродством, которое можно выразить изменением энергии Гиббса или разностью химических потенциалов. Реакционная способность зависит от степени дисперсности вещества, изменение которой может приводить к сдвигу фазового или химического равновесия. Соответствующее приращение энергии Гиббса dGд (благодаря изменению дисперсности) можно представить в виде объединенного уравнения первого и второго начал термодинамики:  Для индивидуального вещества V=Vм и при Т=const имеем:  Подставляя в это уравнение соотношение Лапласа, получим:  для сферической кривизны:  Если рассматривается переход вещества из конденсированной фазы в газообразную, то энергию Гиббса можно выразить через давление пара, приняв его за идеальный. Дополнительное изменение энергии Гиббса, связанное с изменением дисперсности, составляет:  Подставляя данное выражение, получим:  Полученное соотношение называется уравнением Кельвина (уравнение капиллярной конденсации). Для неэлектролитов его можно записать следующим образом:  Из этого уравнения видно, что с увеличением дисперсности растворимость растет, или химический потенциал частиц дисперсной системы больше, чем у крупной частицы, на величину 2σV/r. Степень дисперсности может влиять также на равновесие химической реакции:  С увеличением дисперсности повышается активность компонентов, а в соответствии с этим изменяется константа химического равновесия в ту или другую сторону, в зависимости от степени дисперсности исходных веществ и продуктов реакции. С изменением дисперсности веществ изменяется температура фазового перехода. Количественная взаимосвязь между температурой фазового перехода и дисперсностью вытекает из термодинамических соотношений. Для фазового перехода:  , Для сферических частиц:  Видно, что с уменьшением размера частиц и температуры плавления и испарения вещества уменьшаются (Hф.п.>0).
Основой доказательства теплового молекулярного движения в телах явилось обнаруженное английским ботаником Робертом Броуном в 1827 г. с помощью микроскопа непрерывное движете очень мелких частичек — спор папоротника (цветочной пыльцы), взвешенных в воде. Более крупные частицы находились в состоянии постоянного колебания около положения равновесия. Колебания и перемещения частиц ускорялись с уменьшением их размера и повышением температуры и не были связаны с какими-либо внешними механическими воздействиями. Теоретически обоснованная интерпретация броуновского движения — участие частиц дисперсной фазы ультрамикрогетерогенных систем в тепловом движении — была дана независимо друг от друга Эйнштейнии (1905 г.) и Смолуховским (1906 г.). Проведенными исследованиями была окончательно доказана природа броуновского движения. Молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы, в результате чего она получает огромное число ударов со всех сторон. Э 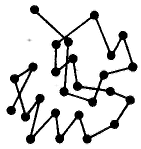 йнштейн и Смолуховский для количественного выражения броуновского движения частиц ввели представление о среднем сдвиге частицы. Если при наблюдении движения частицы золя под микроскопом через определенные равные промежутки времени отмечать ее местонахождение, то можно получить ее траекторию движения. Так как движение происходит в трехмерном пространстве, то квадрат среднего расстояния, проходимого частицей за любой промежуток времени, равен  .Под микроскопом наблюдают проекцию смещения частицы на плоскость за какое-то время, поэтому  .При равновероятных отклонениях частицы ее направление будет находиться между направлениями x и у, т. е. под углом 45° к каждой координате. Отсюда  или  .Из-за равновероятных отклонений среднеарифметическое значение сдвигов равно нулю. Поэтому используются среднеквадратичные расстояния, проходимые частицей:  Эйнштейн и Смолуховский, постулируя единство природы броуновского движения и теплового движения, установили количественную связь между средним сдвигом частицы (называемым иногда амплитудой смещения) и коэффициентом диффузии D. Если броуновское движение является следствием теплового движения молекул среды, то можно говорить о тепловом движении частиц дисперсной фазы. Это означает, что дисперсная фаза, представляющая собой совокупность числа частиц, должна подчиняться тем же статистическим законам молекулярно-кинетической теории, приложимым к газам или растворам. Д 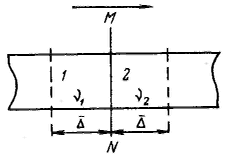 ля установления связи между средним сдвигом (смещением) частицы и коэффициентом диффузии представим себе трубку с поперечным сечением S, наполненную золем, концентрация частиц которого уменьшается слева направо. В этом же направлении протекает и диффузия частиц золя (на рисунке отмечено стрелкой). Выделим по обе стороны от линии MN два малых участка 1 и 2, размеры которых в направлении диффузии равны Δ — среднему квадратичному сдвигу за время τ. Обозначим частичную концентрацию золя в объемах этих участков соответственно через ν1 и ν2 (ν1>ν2). Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от линии MN: половина частиц переместится вправо, а другая половина — влево. Количество дисперсной фазы за время τ переместится из объема 1 вправо:  , а из объема 2 влево (в обратном направлении): .Так как |Q1| > |Q2| (ν1>ν2), то суммарное количество перенесенного вещества через плоскость MN вправо определится соотношением  .Градиент концентрации по расстоянию в направлении диффузии можно выразить так:  Подставляя, получим:  Сравнивая это соотношение с первым законом диффузии Фика:  , окончательно имеем: Это уравнение выражает закон Эйнштейна — Смолуховского, в соответствии с которым квадрат среднего сдвига пропорционален коэффициенту диффузии и времени.
 Экзаменационный билет № 7
Диспергирование и конденсация — методы получения свободно-дисперсных систем: порошков, суспензий, золей, в том числе аэрозолей, эмульсий и т. д. Под диспергированием понимают дробление и измельчение вещества, под конденсацией — образование гетерогенной дисперсной системы из гомогенной в результате ассоциации молекул, атомов или ионов в агрегаты. Работа упругого и пластического деформирования пропорциональна объему тела:  Работа образования новой поверхности при диспергировании пропорциональна приращению поверхности:  Полная работа, затрачиваемая на диспергирование, выражается уравнением Ребиндера:  Разрушение материалов может быть облегчено при использовании эффекта Ребиндера — адсорбционного понижения прочности твердых тел. Этот эффект заключается в уменьшении поверхностной энергии с помощью поверхностно-активных веществ, в результате чего облегчается деформирование и разрушение твердого тела. Процесс конденсации предполагает образование новой фазы на уже имеющихся поверхностях (стенках сосуда, частицах посторонних веществ — ядрах конденсации) или на поверхности зародышей, возникающих самопроизвольно в результате флуктуации плотности и концентраций вещества в системе. В первом случае конденсация называется гетерогенной, во втором — гомогенной. Чтобы сконденсированное вещество не возвращалось в первоначальную фазу и конденсация продолжалась, исходная система должна быть пересыщенной. В противном случае конденсация не может происходить, исчезают и зародыши конденсации (путем их испарения, растворения, плавления). При гомогенной конденсации происходит самопроизвольное образование зародышей; энергия поверхности выступает в качестве потенциального барьера конденсации. Энергию Гиббса образования зародышей выражают (в соответствии с объединенным уравнением первого и второго начал термодинамики) в виде четырех составляющих: энтропийной, механической, поверхностной и химической. Для жидких и газообразных фаз можно ограничиться двумя первыми составляющими энергии Гиббса образования зародышей. Е 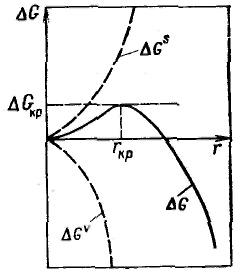 сли степень пересыщения меньше критической, то возникающие зародыши самопроизвольно испаряются (растворяются). Их размеры меньше критического, поэтому энергия Гиббса понижается с уменьшением размера зародыша. Пересыщенный раствор или пар в этих условиях иногда удобно представить как гетерогенно-дисперсную систему, в которой присутствует множество постоянно образующихся и исчезающих зародышей новой фазы. В критической точке неустойчивость равновесия проявляется в том, что существует равная вероятность возникновения и исчезновения зародышей конденсации.Если степень пересыщения больше критической величины, то возникающие зародыши будут самопроизвольно расти. Критическая энергия Гиббса образования зародышей конденсации соответствует критической точке — максимуму функции ΔG = f(r):  Таким образом, энергия Гиббса образования зародышей при гомогенной конденсации равна одной трети поверхностной энергии зародыша. Если найти радиус зародыша в критической точке, приравняв к нулю первую производную от энергии Гиббса и подставить его в данное выражение, то получим:  Из этого соотношения следует, что энергия образования зародыша конденсации зависит от степени пересыщения, от нее же зависит и размер критического радиуса зародыша. Чем выше степень пересыщения, тем ниже энергия Гиббса образования зародышей и тем меньше размеры образующихся зародышей, способных к дальнейшему росту. |