Экзаменационный билет 1
 Скачать 3.38 Mb.
|
 Экзаменационный билет № 25
Потенциальная теория Поляни была предложена для термодинамического описания полимолекулярной адсорбции. Она устанавливает связь величины адсорбции с изменением давления пара (газа) и с теплотами адсорбции, исходя из объема адсорбционного пространства. Наиболее удачно теория Поляни предсказывает зависимость величины адсорбции от температуры. Модель адсорбции в теории Поляни предполагает, что адсорбат ведет себя термодинамически как однокомпонентная система, находящаяся в потенциальном поле поверхностных сил адсорбента, который химически инертен. Теория Поляни принимает, что в адсорбционном пространстве действуют только дисперсионные силы, которые, во-первых, аддитивны, во-вторых, не зависят от температуры. Введено допущение, что практически все адсорбированное вещество находится на поверхности в жидком состоянии. Это допущение в большой мере соответствует состоянию адсорбата в порах пористых адсорбентов. Именно поэтому подход, используемый в теории Поляни, оказался более пригодным для описания адсорбции на пористых адсорбентах, в порах которых происходит конденсация паров. За меру интенсивности адсорбционного взаимодействия принят адсорбционный потенциал — работа переноса 1 моль пара, находящегося в равновесии с жидким адсорбатом в отсутствие адсорбента (давление ps) в равновесную с адсорбентом паровую фазу (давление р):  .Этот потенциал характеризует работу против действия адсорбционных сил. Каждой точке изотермы адсорбции соответствуют определенные значения А и p/ps, которые позволяют получить значения V и ε, т. е. найти зависимости адсорбционного потенциала от объема адсорбата на адсорбенте — потенциальную кривую адсорбции. Т 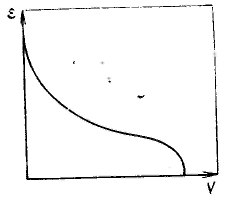 ак как дисперсионные силы не зависят от температуры, то от температуры не должна зависеть и форма потенциальной кривой адсорбции, что экспериментально подтверждается во многих случаях. Экспериментальные точки при разных температурах ложатся на одну и ту же кривую ε = f(V), которую поэтому называют характеристической кривой: , т. е. адсорбционный потенциал при постоянном объеме жидкого адсорбата на адсорбенте (постоянной степени объемного заполнения) не зависит от температуры (температурная инвариантность характеристической кривой).Важная особенность потенциальных кривых адсорбции, заключается в том, что характеристические кривые для одного и того же адсорбента и разных адсорбатов при всех значениях объемов адсорбата в поверхностном слое находятся в постоянном соотношении β:  Коэффициент β был назван коэффициентом аффинности, Отсюда следует, что, зная характеристическую кривую для одного адсорбата и коэффициент аффинности для другого адсорбата по отношению к первому, можно вычислить изотерму адсорбции второго адсорбата на том же адсорбенте.
Рассмотрим зависимость от расстояния энергии притяжения частиц — молекулярной составляющей расклинивающего давления. Из сил Ван-дер-Ваальса наиболее универсальны и существенны лондоновские силы дисперсионного взаимодействия. Энергия электростатического отталкивания пластин равна  .Для вывода уравнения энергии молекулярного притяжении между частицами воспользуемся уравнением энергии притяжения одной молекулы (атома) к поверхности адсорбента (в данном случае частицы):  Приращение энергии молекулярного притяжения, отнесенное к единице площади, пропорционально приращению числа молекул (атомов) в цилиндре с основанием, равным единице площади, т. е. ndr:  После интегрирования получим:  Величина A12 в уравнении называется константой Гамакера. Она учитывает природу взаимодействующих тел. Эта константа выражается в единицах энергии и имеет значение порядка 10-19 Дж. Чем сильнее взаимодействует дисперсная фаза со средой, тем меньше константа Гамакера, это значит, что силы притяжения между частицами уменьшаются. Для области малых потенциалов суммарная энергия взаимодействия равна 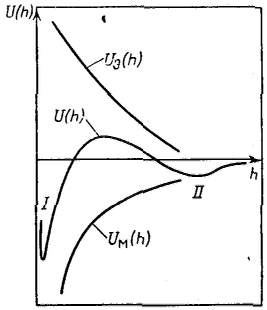  Первичный минимум I отвечает непосредственному слипанию частиц, а вторичный минимум II — их притяжению через прослойку среды. Максимум, соответствующий средним расстояниям, характеризует потенциальный барьер, препятствующий слипанию частиц. Потенциальный барьер увеличивается с уменьшением константы Гамакера.
 Экзаменационный билет № 26
На первый взгляд может показаться, что закономерности заполнения микропор должны следовать теории капиллярной конденсации. Однако размеры микропор таковы, что в них происходит перекрытие полей поверхностных сил противоположных стенок пор, что значительно повышает энергию адсорбции и искажает профиль мениска конденсата в порах, соответствующий уравнению Кельвина, т. е. приводит к дополнительному всасыванию адсорбата, резкому увеличению адсорбционного потенциала. Особенности адсорбции на микропористых телах проявляются в их избирательном действии. Избирательность, или селективность, микропористых адсорбентов существенно выше, чем переходнопористых, благодаря тому, что большинство адсорбированных молекул взаимодействуют непосредственно с поверхностью адсорбента. В более крупных порах такое взаимодействие характерно только для первого слоя. В последующих же слоях взаимодействие не зависит от природы·, адсорбента, а определяется только природой адсорбата. Кроме этой особенности у микропор может проявляться так называемый ситовой эффект, заключающийся в том, что адсорбироваться могут только те молекулы, размеры которых меньше размеров микропор или равны им, в связи с чем все микропористые адсорбенты (не только цеолиты) называют молекулярными ситами. Переходя к количественным соотношениям теории объемного заполнения пор, необходимо отметить, что в ее основе лежат представления потенциальной теории Поляни, предложенной первоначально для описания полимолекулярной адсорбции, исходя из двух основных параметров: адсорбционного потенциала ε, адсорбционного объема V и двух положений:  Степень заполнения адсорбента можно· представить как отношение величины адсорбции А к максимальной адсорбции А0, или как отношение заполненного объема V к предельному объему адсорбционного пространства V0, приведенных к нормальным условиям (давлению и температуре).  или  Эти уравнения являются общими уравнениями теории объемного заполнения микропор. Заменив адсорбционный потенциал на его выражение через давление пара (ε = RTln(p/ps)) и прологарифмировав общее уравнение теории объемного заполнения микропор, получим:  Для большинства активных углей n=2, тогда полученное уравнение переходит в уравнение Дубинина— Радушкевича:  Построение прямой в координатах  дает возможности найти константы этого уравнения A0 и E. Объем микропор Vп рассчитывают по уравнениям
Широкое признание и распространение получила теория устойчивости и коагуляции, учитывающая электростатическую составляющую расклинивающего давления (отталкивание) и его молекулярную составляющую. (притяжение). Эта теория удовлетворительно описывает закономерности поведения типично лиофобных дисперсных систем, для которых можно пренебречь адсорбционно-сольватным фактором устойчивости. В наиболее общем виде эта теория была разработана советскими учеными Б. В. Дерягиным и Л. Д. Ландау в 1937 — 1941 гг. и несколько позднее независимо от них голландскими учеными Фервеем и Овербеком; по первым буквам фамилий этих ученых теория названа теорией ДЛФО. Она рассматривает процесс взаимодействия частиц по отдельным стадиям — перекрывание их поверхностных слоев и возникновение расклинивающего давления, используя при этом понятие потенциального барьера, аналогичное энергии активации в химической кинетике. Расклинивающее давление возникает при сильном уменьшении толщины пленки (прослойки) в результате перекрывания (взаимодействия) поверхностных слоев (поверхностей разрыва). С расклинивающим давлением связана целая область явлений, включающая устойчивость дисперсных систем и пленок, полимолекулярную адсорбцию, набухание, массоперенос в дисперсных системах и др. В гетерогенных системах под пленкой понимают тонкую часть системы, находящуюся между двумя межфззными поверхностями. При уменьшении толщины пленки ограничивающие ее поверхностные слои начинают перекрываться (h<2σ), вследствие чего возникает давление, обусловленное взаимодействием как сближающихся фаз, так и межфазных слоев — расклинивающее давление. Таким образом, избыточные термодинамические функции тонкой пленки зависят от, ее толщины h. 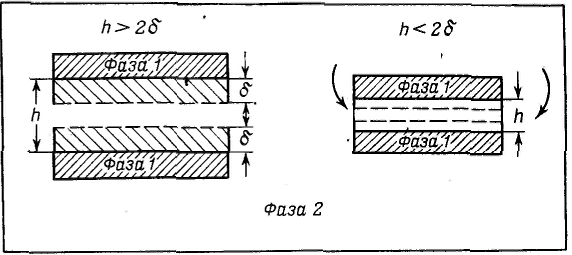 Таким образом, расклинивающее давление можно рассматривать как разность гидростатических давлений в пленке и в окружающей пленку фазе или как приращение энергии Гиббса на данном расстоянии между поверхностными межфазными слоями, пересчитанное на единицу толщины пленки и отнесенное к единице площади перекрывания поверхностных слоев. Расклинивающее давление — суммарный параметр, учитывающий как силы отталкивания, так и силы притяжения, действующие в пленке. Общая энергия взаимодействия между двумя пластинами, приходящаяся на единицу их площади, равна  В теории ДЛФО (в ее классическом виде) принято, что давление отталкивания обусловлено только электростатическими силами, поэтому  .Давление Пэ обусловлено обычно стремлением системы к уменьшению поверхностной энергии, его природа связана с ван-дер-ваальсовыми силами. Для определения электростатической составляющей расклинивающего давления необходимо произвести интегрирование данного уравнения и ряд вычислений, который приведет к значению Пэ:  ,а затем и к  .Р 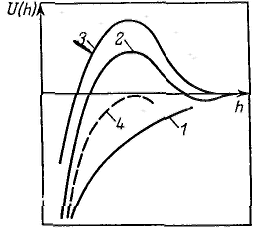 азличают три наиболее характерных вида потенциальных кривых, отвечающих определенным состояниям агрегативной устойчивости дисперсных систем. Кривая 1 соответствует такому состоянию дисперсной системы, при котором на любом расстоянии между частицами энергия притяжения преобладает над энергией отталкивания.Кривая 2 указывает на наличие достаточно высокого потенциального барьера и вторичного минимума. В системе, находящейся в таком состоянии, происходит быстрая флокуляция частиц (перед вторичным минимумом отсутствует потенциальный барьер) на расстояниях, соответствующих вторичному минимуму. Кривая 3 отвечает состоянию системы с высоким потенциальным барьером при отсутствии вторичного минимума или при его глубине, меньшей тепловой энергии (kбT). Вероятность образования агрегатов частиц в таких условиях очень мала, и дисперсные системы обладают большой агрегативной устойчивостью.
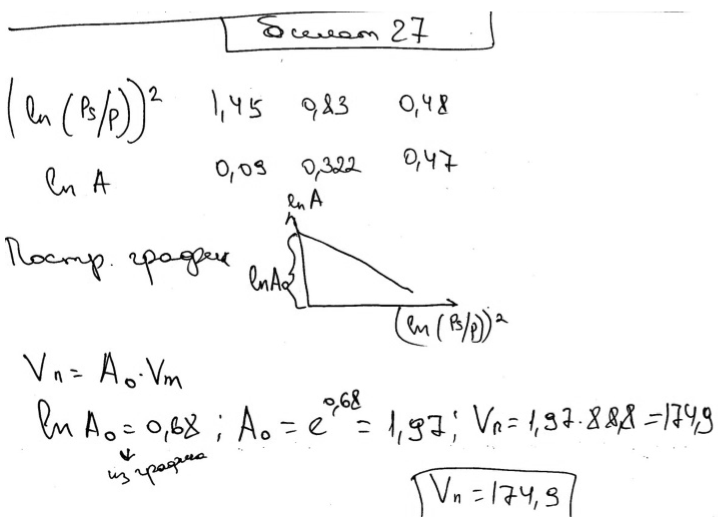
 Экзаменационный билет № 27
Поверхностно-активные вещества (ПАВ), молекулы которых имеют дифильное строение и включают большой углеводородный радикал, отличаются высокой поверхностной активностью по отношению к воде, что отражает сильную зависимость поверхностного натяжения водного раствора ПАВ от их концентрации. Большие значения поверхностной активности предполагают пренебрежимо малые концентрации ПАВ в объеме раствора по сравнению с концентрацией их в поверхностном слое, т. е. с величиной их адсорбции на границе раствор — воздух. Подобная зависимость может обнаруживаться и в растворах других веществ на границе с жидкостью или твердым телом, например при специфическом взаимодействии с поверхностью. Высокая поверхностная активность коллоидных ПАВ зависит, главным образом, от длины углеводородного радикала. Увеличение длины радикала на одну группу CH2 приводит к возрастанию поверхностной активности приблизительно в 3,2 раза (правило Дюклю — Траубе). Это правило соблюдается в основном для истинно растворимых ПАВ. Для органических сред правило Дюкло — Траубе обращается: поверхностная активность снижается с увеличением длины углеводородного радикала ПАВ. Вывод уравнения Шишковского:  После разделения переменных имеем:  После интегрирования получим уравнение Шишковского, характеризующее поверхностное натяжение растворов ПАВ в зависимости от концентрации:  Подобную зависимость σ от с для ПАВ Б. А. Шишковский получил опытным путем. При адсорбции или растекании вещества на поверхности образуется поверхностная (адсорбционная) пленка этого вещества. Полученные ранее уравнения изотерм поверхностного натяжения для ПАВ позволяют перейти к уравнениям состояния поверхностных пленок. При очень малых концентрациях ПАВ распределение вещества между раствором и поверхностным слоем описывается законом Генри, а зависимость поверхностного натяжения от концентрации следует указанному выше соотношению. Если в этом соотношении обозначить  и учесть адсорбционное уравнение, то получим:  Так как величина А обозначает число молей адсорбированного вещества, приходящееся на единицу поверхности, а обратная ей величина Sм=l/A выражает поверхность, на которой распределен 1 моль адсорбированного вещества, то полученному соотношению можно придать вид:  Это уравнение аналогично, уравнению состояния идеального газа. Различие состоит в том, что вместо объема 1 моль газа здесь выступает поверхность, занимаемая 1 моль ПАВ, а вместо давления газа — разность поверхностных натяжений, которая получила название давления двухмерного газа, или двухмерного давления. В соответствии с этим полученное соотношение называют уравнением состояния идеального двухмерного газа. В зависимости от условий, природы ПАВ и подложки образуются поверхностные пленки, которые по свойствам подобны веществам в трех агрегатных состояниях — газообразном, жидком и твердом. Состояние пленки зависит также и от концентрации растекающегося (адсорбирующегося) вещества на поверхности. Если концентрация мала и взаимодействие молекул в поверхностном слое слабое (большой коэффициент растекания), то молекулы ПАВ движутся по поверхности независимо друг от друга. Такое состояние напоминает поведение газа, поэтому пленку называют газообразной. Пленки, образованные при сплошном заполнении поверхностного слоя, 'называют конденсированными. Они могут быть жидкими и твердыми. Твердые пленки обладают структурой, подобной структуре твердого тела. Такая пленка если и течет, то очень медленно. В 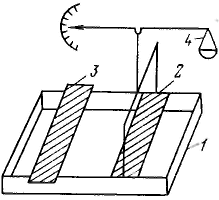 озможность существования поверхностных пленок в различных агрегатных состояниях впервые было наглядно показано Ленгмюром. Он специально сконструировал весы для измерения поверхностного (двухмерного) давления. Принцип метода измерения состоит в следующем. В кювету 1 наливают до краев подлежащую жидкость и на ее поверхность между неподвижной 2 и подвижной 3 планками наносят вещество, образующее мономолекулярную пленку. В процессе теплового движения молекулы вещества ударяются о планку и создают давление, которое можно уравновесить и измерить с помощью разновесов в чашечке 4. Передвигая планку 3, можно изменять площадь, занимаемую молекулами пленки, и тем самым изменять ее двухмерное давление.По зависимости поверхностного давления пленки от площади поверхности, приходящейся на 1 молекулу (1 моль) вещества пленки, можно судить о состоянии пленки. Резкое увеличение поверхностного давления при сжатии пленки отвечает образованию сплошного мономолекул яркого слоя, в котором молекулы плотно прижаты друг к другу. Если площадь sм0, на которой размещен таким образом 1 моль вещества, разделить на число Авогадро, то получим площадь, непосредственно занимаемую одной молекулой: 
Различают следующие термодинамические и кинетические факторы агрегативной устойчивости дисперсных систем: 1. Электростатический фактор заключается в уменьшении межфазного натяжения вследствие возникновения двойного электрического слоя на поверхности частиц в соответствии с уравнением Липпмана. 2. Адсорбционно-сольватный фактор состоит в уменьшении межфазного натяжения при взаимодействии частиц дисперсной фазы со средой (благодаря адсорбции и сольватации) 3. Энтропийный фактор, как и первые два относится к термодинамическим. Он дополняет первые два фактора и действует в системах, в которых частицы или их поверхностные слои участвуют в тепловом движении. 4. Структурно-механический фактор является кинетическим. Его действие обусловлено тем, что на поверхности частиц имеются пленки, обладающие упругостью и механической прочностью, разрушение которых требует затраты энергии и времени. 5. Гидродинамический фактор снижает скорость коагуляции благодаря изменению вязкости среды и плотности дисперсной фазы и дисперсионной среды. 6. Смешанные факторы наиболее характерны для реальных систем. Обычно агрегативная устойчивость обеспечивается несколькими факторами одновременно. Коагуляция протекает в термодинамически неустойчивых (лиофобных) дисперсных системах, и об агрегативной устойчивости таких систем судят по скорости коагуляции. Коагуляция может происходить как без внешнего воздействия на систему, так и при повышении температуры, межаническом, электрическом или другом воздействии, а в случае золей – при ведении коагулянтов, например электролитов. Принято считать, что типичные лиофобные системы агрегатнвно устойчивы благодаря проявлению электростатического фактора стабилизации и коагулируют при введении в систему сравнительно небольших количеств любых электролитов. Наименьшая концентрация электролита см, при которой начинается коагуляция (медленная), называется порогом коагуляции. Для осуществления быстрой коагуляции требуется такая концентрация электролита сб, после увеличения которой скорость коагуляции остается постоянной (когда фактор устойчивости W=1, или потенциальный барьер ΔE = 0). З 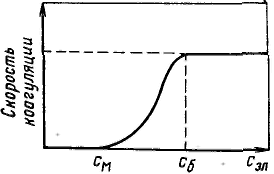 ависимость скорости коагуляции от концентрации электролита показана на рисунке. Из этого рисунка следует, что введение электролита в дисперсную систему снижает потенциальный барьер, который при быстрой коагуляции (максимальной скорости) становится равным нулю. Порог коагуляции существенно зависит от момента его фиксирования, от метода наблюдения за коагуляцией (изменение интенсивности рассеяния света, реологических свойств и др.) и от концентрации золя, поэтому необходимо всегда подробно указывать условия определения этой величины.В соответствии с теорией ДЛФО введение электролита в дисперсную систему вызывает сжатие двойного электрического слоя на поверхности частиц, вследствие чего они могут подойти друг к другу на расстояния, на которых преобладают силы притяжения. Уменьшение толщины двойного слоя сопровождается обменом противоионов этого слоя на вызывающие коагуляцию ионы электролита. Закон Дерягина:  При высоких потенциалах порог быстрой коагуляции по теории ДЛФО не зависит от потенциала и обратно пропорционален заряду противоиона в шестой степени, что хорошо обосновывает известное эмпирическое правило Шульце — Гарди. По правилу Шульце — Гарди значения порогов коагуляции для электролитов с зарядами противоионов 1, 2, 3 находятся в соотношении  .Чтобы обеспечить агрегативную устойчивость дисперсных систем, частицы которых имеют лиофобную поверхность, применяют стабилизаторы, способствующие увеличению межфазного взаимодействия. В качестве таких стабилизаторов широко применяют ПАВ и ВМС (имеющие неполярные и полярные части молекул), лиофилизируюшие поверхность частиц дисперсной фазы. Стабилизацию лиофобных дисперсных систем с помощью лнофильных коллоидов (в первую очередь, ВМС) называют защитным действием стабилизаторов — коллоидной защитой.
 |