Лекция по электротехнике постоянный ток. Лекция ЭЛЕКТРОТЕХНИКА Постоянный. Электрические цепи постоянного тока и методы их расчета Электрическая цепь и ее элементы

• Название: Электрические цепи постоянного тока и методы их расчета Электрическая цепь и ее элементы
• Анкор: Лекция по электротехнике постоянный ток
• Дата: 17.05.2022
• Размер: 292.71 Kb.
• Имя файла: Лекция ЭЛЕКТРОТЕХНИКА Постоянный.docx
• Тип: Задача; #534568
• страница: 3 из 4

1.6. Режимы работы электрической цепи

При подключении к источнику питания различного количества потребителей или изменения их параметров будут изменяться величины напряжений, токов и мощностей в электрической цепи, от значений которых зависит режим работы цепи и ее элементов.

Реальная электрическая цепь может быть представлена в виде активного и пассивного двухполюсников (рис. 1.23).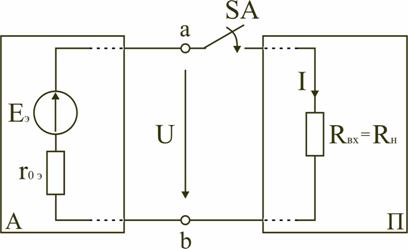



Рис. 1.23

Двухполюсником называют цепь, которая соединяется с внешней относительно нее частью цепи через два вывода а и b – полюса.

Активный двухполюсник содержит источники электрической энергии, а пассивный двухполюсник их не содержит. Для расчета цепей с двухполюсниками реальные активные и пассивные элементы цепи представляются схемами замещения. Схема замещения пассивного двухполюсника П представляется в виде его входного сопротивления

.

Схема замещения активного двухполюсника А представляется эквивалентным источником с ЭДС E_э и внутренним сопротивлением r_0э, нагрузкой для которого является входное сопротивление пассивного двухполюсника R_вх=R_н.

Режим работы электрической цепи (рис. 1.23) определяется изменениями параметров пассивного двухполюсника, в общем случае величиной сопротивления нагрузки R_н. При анализе электрической цепи рассматривают следующие режимы работы: холостого хода, номинальный, короткого замыкания и согласованный.

Работа активного двухполюсника под нагрузкой R_н определяется его вольт-амперной (внешней) характеристикой, уравнение которой (1.10) для данной цепи запишется в виде

(1.12)

U=E_э−Ir_0э.

Эта вольт-амперная характеристика строится по двум точкам 1 и 2 (рис. 1.24), соответствующим режимам холостого хода и короткого замыкания.

1. Режим холостого хода

В этом режиме с помощью ключа SA нагрузка R_н отключается от источника питания (рис. 1.23). В этом случае ток в нагрузке становится равным нулю, и как следует из соотношения (1.12) напряжение на зажимах ab становится равным ЭДС E_э и называется напряжением холостого хода U_хх

U=U_хх=E_э.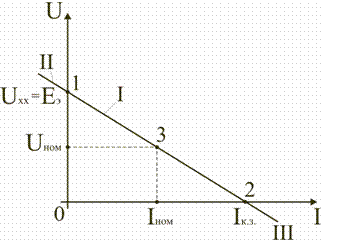



Рис. 1.24

2. Режим короткого замыкания

В этом режиме ключ SA в схеме электрической цепи (рис. 1.23) замкнут, а сопротивление R_н=0. В этом случае напряжение U на зажимах аb становится равным нулю, т.к. U=IR_н, а уравнение (1.12) вольт-амперной характеристики можно записать в виде

(1.13)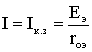

.

Значение тока короткого замыкания I_к.з соответствует т.2 на вольт-амперной характеристике (рис. 1.24).

Анализ этих двух режимов показывает, что при расчете электрических цепей параметры активного двухполюсника E_э и r_0э могут быть определены по результатам режимов холостого хода и короткого замыкания:

(1.14)

E_э=U_хх;  .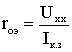

При изменении тока в пределах   активной двухполюсник (эквивалентный источник) отдает энергию во внешнюю цепь (участок I вольт-амперной характеристики на рис. 1.24). При токе I<0 (участок II) источник получает энергию из внешней цепи, т.е. работает в режиме потребителя электрической энергии. Это произойдет, если к зажимам аb двухполюсника присоединена внешняя цепь с источниками питания. При напряжении U<0 (участок III) резисторы активного двухполюсника потребляют энергию источников из внешней цепи и самого активного двухполюсника.

3. Номинальный режим

Номинальный режим электрической цепи обеспечивает технические параметры как отдельных элементов, так и всей цепи, указанные в технической документации, в справочной литературе или на самом элементе. Для разных электротехнических устройств указывают свои номинальные параметры. Однако три основных параметра указываются практически всегда: номинальное напряжение U_ном, номинальная мощность P_ном и номинальный ток I_ном.

Работа активного двухполюсника под нагрузкой в номинальном режиме определяется уравнением (1.12), записанном для номинальных параметров

(1.15)

U_ном=E_э−I_номr_0э.

На вольт-амперной характеристике (рис. 1.24) это уравнение определяется точкой 3 с параметрами U_ном и I_ном.

4. Согласованный режим

Согласованный режим электрической цепи обеспечивает максимальную передачу активной мощности от источника питания к потребителю. Определим параметры электрической цепи (рис. 1.23), обеспечивающие получение согласованного режима. При подключении нагрузки R_н к активному двухполюснику (рис. 1.23) в ней возникает ток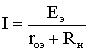

.

При этом на нагрузке выделится активная мощность

(1.16)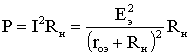

.

Определим соотношение между сопротивлением нагрузки R_н и внутренним сопротивлением r_0э эквивалентного источника ЭДС, при котором в сопротивлении нагрузки R_н выделяется максимальная мощность при неизменных значениях E_э и r_0э. С этой целью определим первую производную P по R_н и приравняем ее к нулю: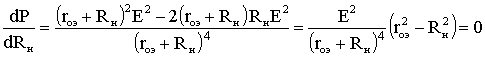

.

Так как выражение в знаменателе – конечное, то, отбрасывая не имеющее физического смысла решение R_н=−r_0э, получим, что значение сопротивления нагрузки, согласованное с сопротивлением источника

(1.17)

R_н=r_0э.

Можно найти вторую производную и убедиться в том, что она отрицательна 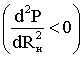 , поэтому соотношение (1.17) соответствует максимуму функции P=F(R_н).

Подставив (1.17) в (1.16), получим значение максимальной мощности, которая может выделена в нагрузке R_н

(1.18)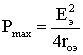

.

Полезная мощность, выделяющаяся в нагрузке, определяется уравнением (1.16). Полная активная мощность, выделяемая активным двухполюсником,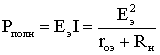

.

Коэффициент полезного действия

(1.19)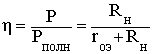

.

если R_н=r_0э, то  .

Для мощных электротехнических устройств такое низкое значение КПД недопустимо. Но в электронных устройствах и схемах, где величина P измеряется в милливаттах, с низким КПД можно не считаться, поскольку в этом режиме обеспечивается максимальная передача мощности на нагрузку.

1.7. Расчет электрических цепей с использованием законов Ома и Кирхгофа

Законы Ома и Кирхгофа используют, как правило, при расчете относительно простых электрических цепей с небольшим числом контуров, хотя принципиально с их помощью можно рассчитать сколь угодно сложные электрические цепи.

При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС или напряжения, сопротивления элементов электрической цепи, и задача сводится к определению токов в ветвях цепи. Зная токи, можно найти напряжения на элементах цепи, мощность, потребляемую отдельными элементами и всей цепью в целом, мощность источников питания и др.

Расчет цепи с одним источником питания

Электрическая цепь, схема которой приведена на рис. 1.25, состоит из одного источника питания, имеющего ЭДС E и внутреннее сопротивление r₀, и резисторов R₁,R₂,R₃, подключенных к источнику по смешанной схеме. Операции расчета такой схемы рекомендуется производить в определенной последовательности.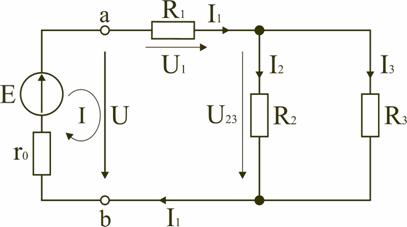



Рис. 1.25

1. Обозначение токов и напряжений на участках цепи.

Резистор R₁ включен последовательно с источником, поэтому ток I₁ для них будет общим, токи в резисторах R₂ и R₃ обозначим соответственно I₂ и I₃. Аналогично обозначим напряжения на участках цепи.

2. Расчет эквивалентного сопротивления цепи.

Резисторы R₂ и R₃ включены по параллельной схеме и заменяются согласно (1.7) эквивалентным сопротивлением:

.

В результате цепь на рис. 1.25 преобразуется в цепь с последовательно соединенными резисторами R₁,R₂₃ и r₀. Тогда эквивалентное сопротивление всей цепи запишется в виде:

R_э=r₀+R₁+R₂₃

3. Расчет тока в цепи источника. Ток I₁ определим по закону Ома (1.2):

I₁=U/R_э

4. Расчет напряжений на участках цепи. По закону Ома (1.1) определим величины напряжений:

U₁=I₁R₁; U₂₃=I₁R₂₃

Напряжение U на зажимах ab источника питания определим по второму закону Кирхгофа (1.4) для контура I (рис. 1.25):

E=I₁r₀+U; U=E−I₁r₀.

5. Расчет токов и мощностей для всех участков цепи. Зная величину напряжения U₂₃, определим по закону Ома токи в резисторах R₂ и R₃: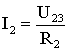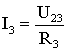

;  .

По формуле (1.8) определим величину активной электрической мощности, отдаваемую источником питания потребителям электрической энергии:

P=EI₁.

В элементах схемы расходуются активные мощности:

;  ;  .

На внутреннем сопротивлении r₀ источника питания расходуется часть электрической мощности, отдаваемой источником. Эту мощность называют мощностью потерь  :

.

6. Проверка правильности расчетов. Эта проверка производится составлением уравнения баланса мощностей (1.8): мощность, отдаваемая источником питания, должна быть равна сумме мощностей, расходуемых в резистивных элементах схемы:

.

Кроме того, правильность вычисления токов можно проверить, составив уравнение по первому закону Кирхгофа (1.3) для узла схемы:

I₁=I₂+I₃.

Расчет разветвленной электрической цепи с несколькими источниками питания

Основным методом расчета является метод непосредственного применения первого и второго законов Кирхгофа.

В качестве примера рассмотрим цепь, схема которой приведена на рис. 1.26. Схема цепи содержит 6 ветвей (m=6) и 4 узла: a, b, c, d (n=4). По каждой ветви проходит свой ток, следовательно число неизвестных токов равно числу ветвей, и для определения токов необходимо составить m уравнений. При этом по первому закону Кирхгофа (1.3) составляют уравнения для (n–1) узлов. Недостающие m–(n–1) уравнения получают по второму закону Кирхгофа (1.4), составляя их для m–(n–1) взаимно независимых контуров. Рекомендуется выполнять операции расчета в определенной последовательности.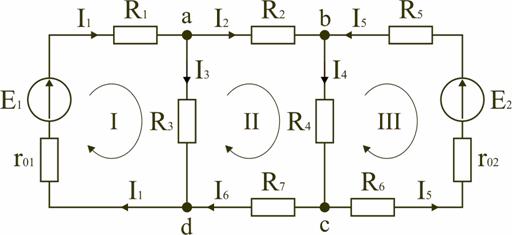



Рис. 1.26

1. Обозначение токов во всех ветвях. Направление токов выбираем произвольно, но в цепях с источниками ЭДС рекомендеются, чтобы направление токов совпадало с направлением ЭДС.

2. Составление уравнений по первому закону Кирхгофа. Выбираем 4–1=3 узла (a, b, c) и для них записываем уравнения:

узел a: I₁−I₂−I₃=0;

узел b: I₂−I₄+I₅=0;

узел c: I₄−I₅+I₆=0.

3. Составление уравнений по второму закону Кирхгофа. Необходимо составить 6–3=3 уравнения. В схеме на рис. 1.26 выбираем контура I, II, III и для них записываем уравнения:

контур I: E₁=I₁(r₀₁+R₁)+I₃R₃;

контур II: 0=I₂R₂+I₄R₄+I₆R₇−I₃R₃;

контур III: −E₂=−I₅(r₀₂+R₅+R₆)−I₄R₄.

4. Решение полученной системы уравнений и анализ результатов. Полученная система из шести уравнений решается известными математическими методами. Если в результате расчетов численное значение тока получено со знаком «минус», это означает, что реальное направление тока данной ветви противоположно принятому в начале расчета. Если в ветвях с ЭДС токи совпадают по направлению с ЭДС, то данные элементы работают в режиме источников, отдавая энергию в схему. В тех ветвях, где направления тока и ЭДС не совпадают, источники ЭДС работает в режиме потребителя.

5. Проверка правильности расчетов. Для проверки правильности произведенных расчетов можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы уравнений:

узел d: I₃+I₆−I₁=0

внешний контур схемы: E₁−E₂=I₁(r₀₁+R₁)+I₂R₂−I₅(r₀₂+R₅+R₆)+I₆R₇.

Независимой проверкой является составление уравнения баланса мощностей (1.8) с учетом режимов работы элементов схемы с ЭДС:

.

Если активная мощность, поставляемая источниками питания, равна по величине активной мощности, израсходованной в пассивных элементах электрической цепи, то правильность расчетов подтверждена.