Электрических цепей постоянного тока

• Название: Электрических цепей постоянного тока
• Дата: 23.07.2022
• Размер: 5.4 Mb.
• Имя файла: materialy-dlya-dlya-studentov-fakulteta-elektrifikacii-po-podgot.doc
• Тип: Закон; #635135
• страница: 6 из 8

Тема 4

РАСЧЕТ МОЩНОСТЕЙ В ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Цель: Изучить методику расчета мощностей и определения пока­заний ваттметра.
4.1. Задание по самоподготовке
1. Повторить закон Ома для цепи синусоидального тока [1] § 3.12, треугольник сопротивлений [1] § 3.14.

2. Проработать по учебным пособиям тему "Мощности в цепи синусоидаль­ного тока".

3. Изучить этот же материал по учебнику [1] § 1.11, § 1.27, 3.6, 3.21...3.24 , 3.32.

4.Рассмотреть примеры п. 4.3 данных указаний и примеры 40, 42 по учебнику [1].

5. Ответить на контрольные вопросы п. 4. 6.
4.2 Общие сведения
Мгновенная мощность p, получаемая приемником цепи, находится как произведение мгновенных значений напряжения и тока.

Активная мощность P есть среднее значение мгновенной мощности за период Т

.

Подставляя выражение мгновенной мощности р, получим формулу активной мощности синусоидального тока:



Множитель соs носит название коэффициента мощности.

Активная мощность Р физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты на участке цепи с сопротивлением R.

Так как , то активная мощность может иметь еще следующие выражения

.

Активная мощность измеряется в ваттах (Вт).

При расчетах электрических цепей пользуются также понятием реактивная мощность, которая определяется по формуле

.

Реактивная мощность характеризует ту часть энергии, которая колеблется между приемником и источником.

Так как , то величина реактивной мощности в це­пи переменного тока может быть выражена следующим образом:

.

Реактивная мощность измеряется в вольт-амперах реактивных (вар). Если sinφ > 0, то Q > О, если sinφ < O , тоQ < О . Так как X = Х_L – Х_C , то

.

Наряду с понятием активной мощности Р и реактивной Q , применяется понятие полной мощности S :

S = UI.

Математически произведение UI = S представляет наибольшую возможную активную мощность Р, которую можно получить при заданных значениях U и I и при сдвиге фаз φ = 0 , т.е. cos φ = 1.

Так как

.

Полная мощность измеряется в вольт-амперах (В·А).

Между Р, Q и S существует соотношение 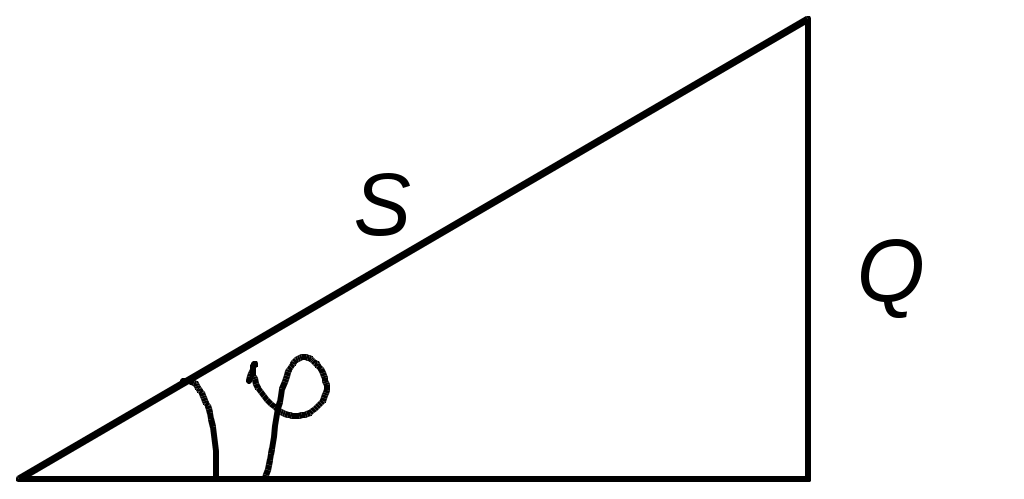. Графически эту связь можно представить в виде прямоугольного треугольника (рис. 4.1). Из треугольника мощностей видно, что P = S cosj; Q = Ssinj = Ptgj.



Рис. 4.1. Треугольник мощностей

По измеренным или вычисленным значениям тока I, напряжения U и мощности Р приемника легко определяются параметры приемника R , X , Z .

, , , .

Реактивное сопротивление Х > 0 , если X_L >X_C , если Х < 0, если X_L < X_C.

Комплексная мощность ,

где ­- сопряженная комплексная величина (сопряженный комплекс тока).
4.3. Примеры
4.3.1. К последовательно соединенным реостату с сопротивлением 120 Ом и конденсатору С = 30 мкФ подведено напряжение u = 311 sin 314 t (рис. 4.2). Определить активную, реактивную и полную мощности и коэффициент мощности.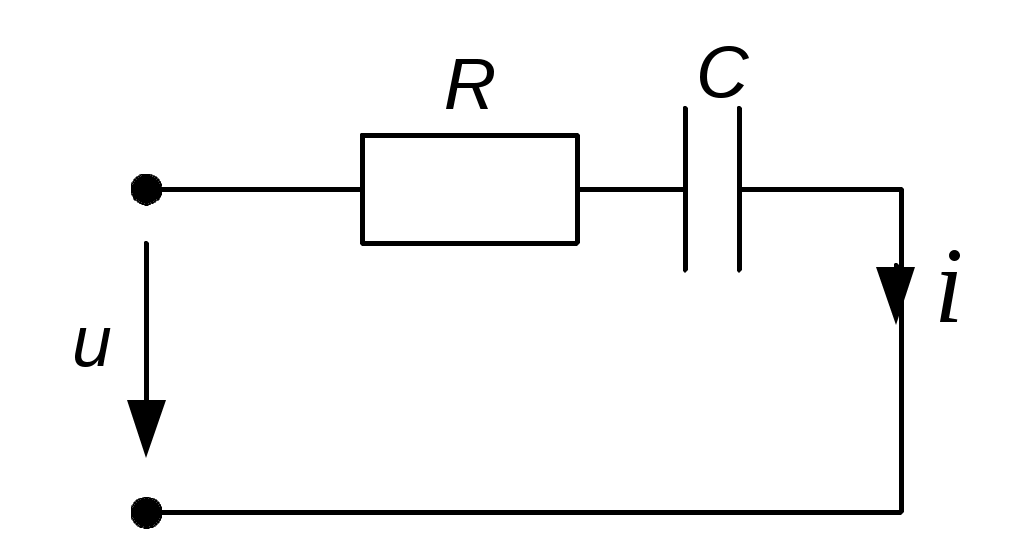



Рис. 4.2

Решение

Действующее значение напряжения



Емкостное сопротивление



Полное сопротивление цепи



Действующее значение тока



Из треугольника сопротивлений коэффициент мощности



Активная мощность

Вт.

Из треугольника сопротивлений



Реактивная мощность

.

Реактивная мощность отрицательная, так как реактивное сопро­тивление для данной цепи X = Х_L  –  Х_C отрицательно (Х_L = 0).

Полная мощность

.

4.3.2. В цепи установлены сварочный аппарат мощностью Р₁ = 6 кВт при cosφ₁ = 0,5, электрический двигатель P₂ = 12 кВт при cosφ₂ = 0,8 и батарея конденсаторов мощностью Q_C = 10 квар, при cosφ₃ = 0. Напряжение цепи U = 220 В. Определить cosφ всей цепи и общий ток I.

Решение

Для определения коэффициента мощности всей цепи используем выражение сosφ = P/S, где активная мощность всей цепи Р = Р₁ + Р₂ = 6 + 12 = =18 кВт, полная мощность всей цепи .

Реактивную мощность Q всей цепи определим после расчета реактивных мощностей потребителей: Q₁=P₁·tgφ₁,

φ₁ = arccos 0,5 = 60°,

Q₁ = 6·tg60° = 6·1,73 = 10,4 квар,

Q₂ = P₂·tgφ₂ = 12·tg37° = 12·0,75 = 9 квар,

φ₂ = arccos 0,8 = 37°.

Реактивная мощность всей цепи

Q = Q₁  +  Q₂ – Q_C = 10,4  +  9 – 10 = 9,4 квар.

Реактивная мощность батареи конденсаторов взята со знаком “минус”, так как для емкости φ = - 90° и Q = U I sinφ < 0.

Полная мощность всей цепи

.

Коэффициент мощности всей цепи

.

Общий ток найдем из выражения полной мощности S = U I, откуда

I = S/U = 20 300/220 = 92,2A.

4.3.3. Определить показание ваттметра (рис. 4.3.)

Дано: U = 100 B; R₁ = 2 Ом; R₂ = 10 Ом; R₃ = 20 Ом;

X₁ = 14 Ом; X₂ = 20 Ом; X₃ = 30 Ом.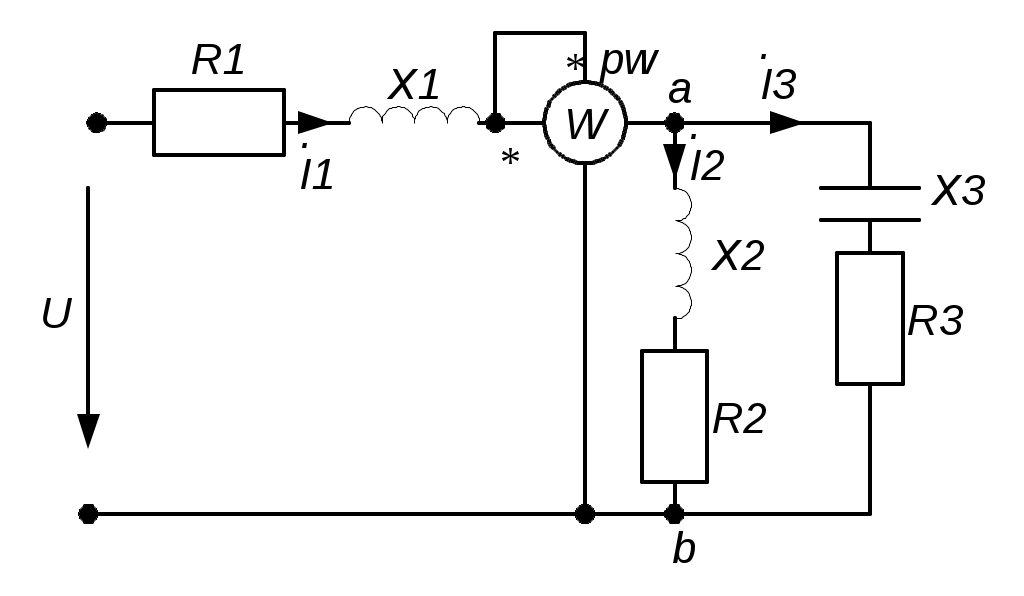



Рис. 4.3

Решение

Показание ваттметра , где U_w  –  напряжение, к которому подключен ваттметр; I_w  –  ток, проходящий через ват­тметр,  –  угол сдвига фаз напряжения и тока. Следова­тельно, для определения показания ваттметра, включенного по схеме рис. 4.3, нужно определить напряжение U_аb, ток I₁ и сдвиг фаз между ними.

Так как электрическая цепь имеет смешанное соединение сопро­тивлений, расчет ведем в комплексной форме.

Сопротивление параллельно соединенных ветвей



Общее сопротивление цепи



Ток на входе цепи, проходящий через ваттметр



Действующее значение тока



Начальная фаза тока



Напряжение на ваттметре определим по второму закону Кирхгофа



Действующее значение напряжения



Начальная фаза напряжения



Показание ваттметра

Вт.

Показание ваттметра можно рассчитать более просто, используя комплексную мощность , где  –  сопряженный комплекс тока



Показание ваттметра равно действительной части комплексной мощности: P_w=184 Вт.

4.4. Задачи для самостоятельного решения
4.4.1. Известны мгновенные значения напряжения и тока электрической цепи:

u = 141sin(ωt + 45°); i = 14,1sin(ωt – 15°). Определим активную, реактивную и полную мощности цепи.

Ответ: Р = 500 Вт; Q = 866 вар; S = 1 000 ВА.
4.4.2. Для определения параметров индуктивной катушки была собрана цепь по схеме рис. 4.4. Приборы показали: U = 100 В; I = 5 А; P = = 300 Вт. Определить активное сопротивление R и индуктивность L катушки, если частота f = 50 Гц. Ответ: R = 12 Ом; L = 0,051 Гн.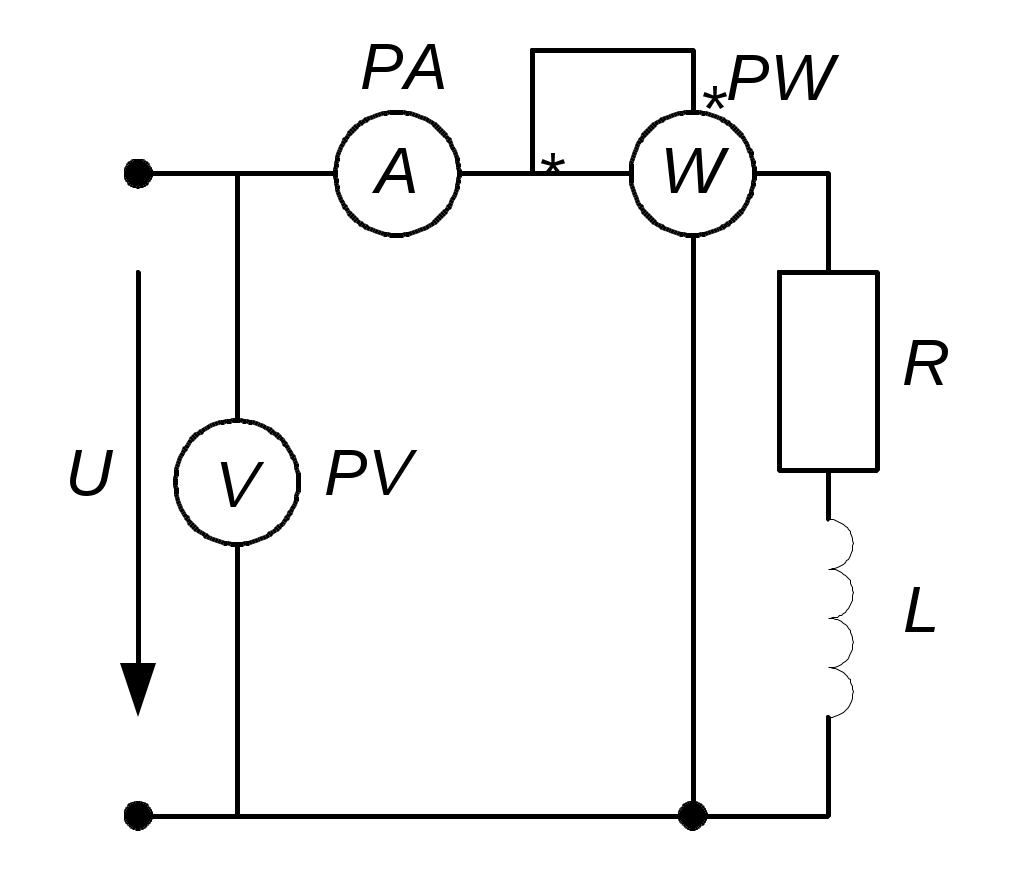



Рис. 4.4

4.4.3. В электрической цепи (рис.11.5) действующее значение синусоидальной ЭДС Е =100 В; R₀ = 4 Ом; R₁ = 6 Ом ; X_L = 5 Ом; X_C= 10 Ом.

Определить показания ваттмет­ра (рис. 4.5). Ответ: Р = 300 Вт.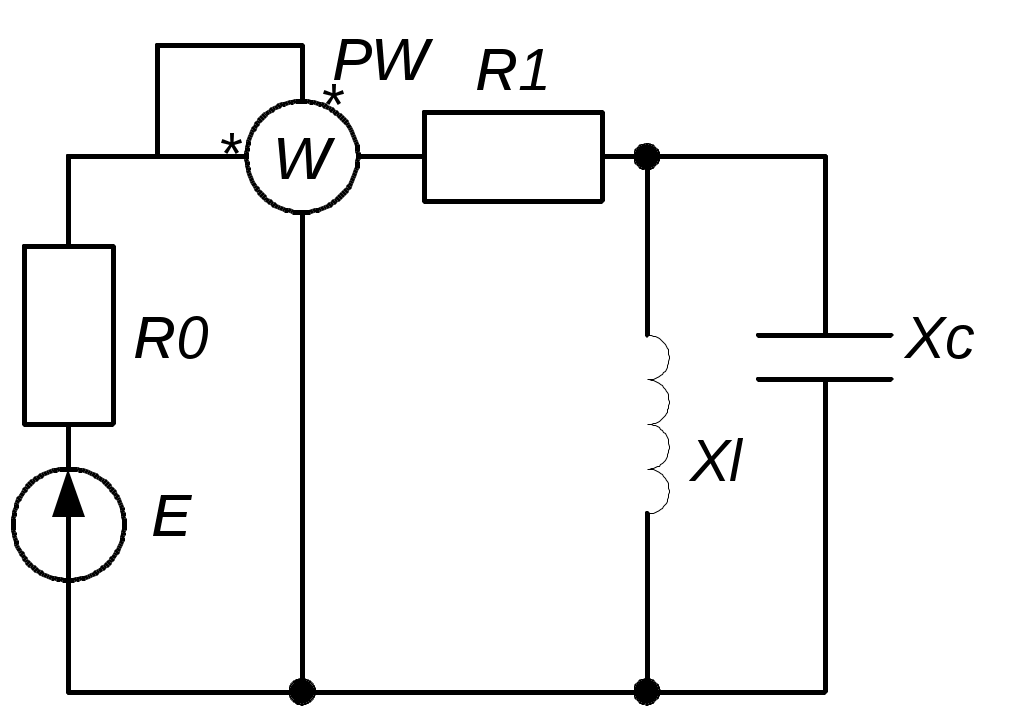



Рис. 4.5
4.5. Индивидуальные задания
К источнику с синусоидальным напряжением U подключена цепь со смешанным соединением сопротивлений (таб­лица 4.1.) Нарисовать схему цепи. На входе цепи включить ват­тметр для измерения активной мощности всей цепи. Определить показа­ние ваттметра.
Таблица 4.1

N варианта	U, B	Ом	Ом	Ом
1	100	2,6 – j2,8	2 – j2	– j2
2	50	0,6  +  j0,1	1  +  j2	3
3	200	9  +  j3	j10	10  +  j20
4	50	1 – j3	4  +  j2	– j5
5	100	2,6  +  j2,8	2  +  j2	j2
6	400	18 + j1	30	10 + j20
7	10	0,2 + j0,6	1 + j1	2
8	40	0,8 + j2,9	3	1 – j2
9	80	0,9 + j0,3	1 + j2	j1
10	50	0,2 + j0,4	4	j2
11	100	0,8 +j0,6	2	2 + j2
12	200	1,8 +j2,6	1 + j2	-j4
13	100	2 – j4	-j5	3 + j1
14	200	5 + j5	10	j10
15	75	3j	2 + j2	-j4
16	200	-j10	10j	5 – j5
17	10	0,1 + j0,7	1	j3
18	80	0,4  +  j1,2	2	j4

4.6. Контрольные вопросы
1. Что понимают под активной, реактивной и полной мощностями? В каких единицах они измеряются?

2. Какие значения тока и напряжения входят в формулы Р, Q , S ?

3. Что такое угол φ, чем вызвано появление угла φ и в каких пределах он может находиться?

4. Почему cosφ назван коэффициентом мощности, что он показывает?

5. Почему стремятся повысить cosφэлектроустановок?

6. Сколько обмоток у ваттметра, как они называются и как включаются?

7. Как рассчитывается комплексная мощность?

Тема 5

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

ПРИ РЕЗОНАНСНЫХ ЯВЛЕНИЯХ

Цель: Изучить особенности расчета электрических цепей в резонансном режиме
5.1 Задание по самоподготовке
1. Повторить закон Омa для цепи синусоидального тока [1] §3.12.

2. Проработать лекции по теме "Резонанс в электрических цепях”.

3. Изучить этот же материал по учебнику [1] § 3.25...3.28.

4. Рассмотреть примеры п. 12.3. данных указаний и пример 43 по учебнику [1] .

5. 
   Ответить на контрольные вопросы п. 5.6.
   

5.2 Общие сведения
Под резонансным режимом двухполюсника, содержащего индуктивности и емкости, понимают режим, при котором входное сопротивление двухполюсника является чисто активным.

Ток и напряжение на входе двухполюсника, находящегося в ре­зонансном режиме, совпадают по фазе, реактивная мощность двухпо­люсника при этом равна нулю.

Резонанс при последовательном соединении R , L , С называют резонансом напряжений. Он наступает при условии .

Резонансная частота

Напряжения U_L = U_C могут превышать напряжение на входе цепи при условии .

Добротность контура

Характеристическое сопротивление .

Резонанс в цепи c параллельным соединением ветвей, содержащих индуктивность и емкость, называется резонансом токов. Для цепи рис. 5.1 условие резонанса b_L = b_С или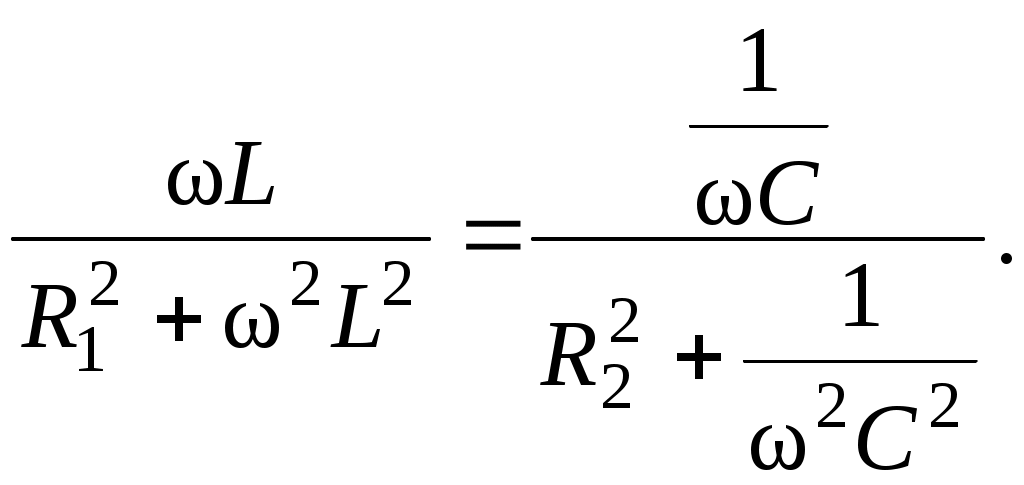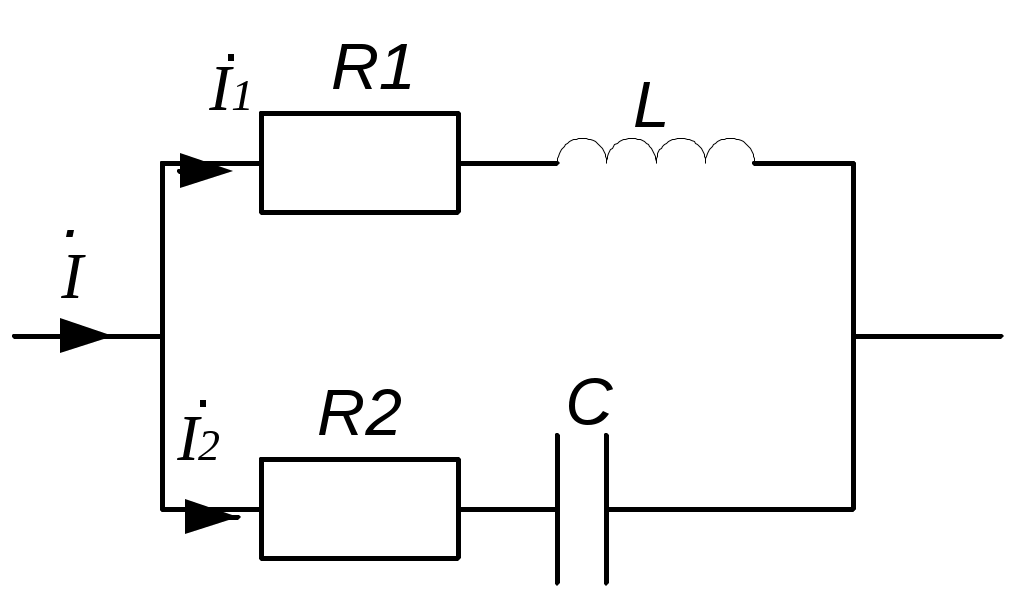





Рис.5.1 исправить (Убрать токи обозначить I1, I2, I3)

Явление, происходящее в цепи рис.5.1 можно наглядно предста­вить с помощью векторной диаграммы (рис. 5.2).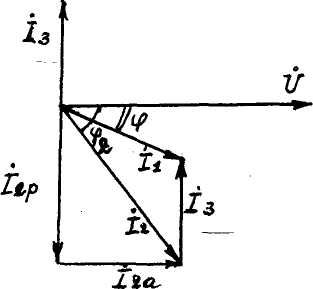



Рис. 5.2 Векторная диаграмма

Ток I₂ в приемнике R , L отстает от приложенного напряжения U на угол φ₂ . Ток I₃ в конденсаторе С опережает напряже­ние на 90°. Общий ток в неразветвленной части цепи равен векторной сумме токов обеих ветвей

.

При отсутствии конденсатора общий ток равнялся бы току I₂ . Как видно из векторной диаграммы, при параллельном подключении конденсатора к приемнику R, L, во-первых, уменьшается общий ток цепи I₁, во-вторых, уменьшается угол φ между общим то­ком I₁ и напряжением, следовательно, увеличивается коэффициент мощности cos φ.

Уменьшение угла сдвига фаз напряжения на приемнике и общего тока называют компенсацией сдвига фаз.

Практически целесообразность уменьшения угла φ заключается в одновременном уменьшении общего тока I₁, что приводит к снижению потерь мощности в линии, соединяющей потребитель с источником, так как потери в линии пропорциональны квадрату тока.

Минимальную величину общего тока можно получить в том слу­чае, когда ток в конденсаторе будет равен реактивной составля­ющей тока I₂

; .

Эти токи будут полностью компенсировать друг друга благо­даря тому, что имеют сдвиг по фазе на 180°. Этот случай носит название резонанса токов. При резонансе общий ток в неразветвленной части цепи совпадает по фазе с напряжением, т.е. ста­новится чисто активным, угол φ = 0, cos φ = 1.

С увеличением тока в конденсаторе сверх необходимого для компенсации реактивной составляющей тока I₂ общий ток будет рас­ти, угол φ приобретает отрицательное значение и увеличивает­ся, коэффициент мощности уменьшается.

Аналитический расчет параллельных цепей переменного тока про­водится с помощью проводимостей. В данном случае общий ток цепи

,

где U– напряжение, приложенное к цепи;

У – полная проводимость цепи,

g– активная проводимость ветви R, L; ,

b_L– индуктивная проводимость ветви R, L; ,

b_С – емкостная проводимость ветви с емкостью; .

Изменяя или индуктивность L, или емкость С, или сопро­тивление R , или частоту питающего напряжения, можно достичь того, что b_L будет равняться b_C , и тогда общий ток I₁ = Ug становится чисто активным. Это соответствует режиму резонанса. Следовательно, условие резонанса токов можно записать как b_L= b_Cили

.

В частном случае, когда можно пренебречь активным сопротив­лением катушки индуктивности, условием резонанса становится равенство или . В этом частном случае ток в неразветвленной части цепи равен нулю. Это значит, что притока энергии извне нет, но в замкнутом контуре, образуемом двумя ветвями, ток проходит. В этом контуре происходит непрерывное превращение энергии электрического поля, запасенного конден­сатором, в энергию магнитного поля, запасаемую катушкой, и обратно.

Явление резонанса токов используется для увеличения коэффи­циента мощности электрических установок, в радиотехнике и тех­нике связи.

5.3 Примеры
5.3.1. В электрической цепи (рис.5.3) R = 100 Ом; L = =5,05 мГн; C = 0,05 мкФ; U = 10 B.



Pис. 5.3
Вычислить резонансную частоту, добротность контура, напряжения

U_R,U_L,U_C. Построить векторную диаграмму.
Решение

Резонансная частота



Добротность контура

.

Емкостное сопротивление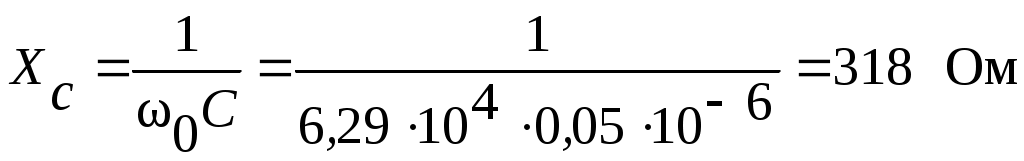

.

Полное сопротивление цепи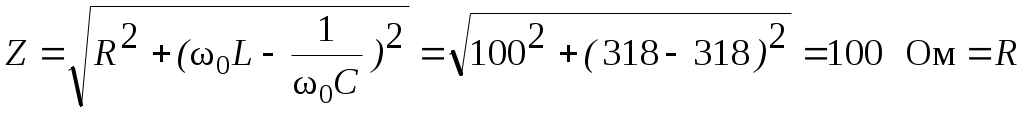

, то есть  резонансная частота определена верно.

Ток цепи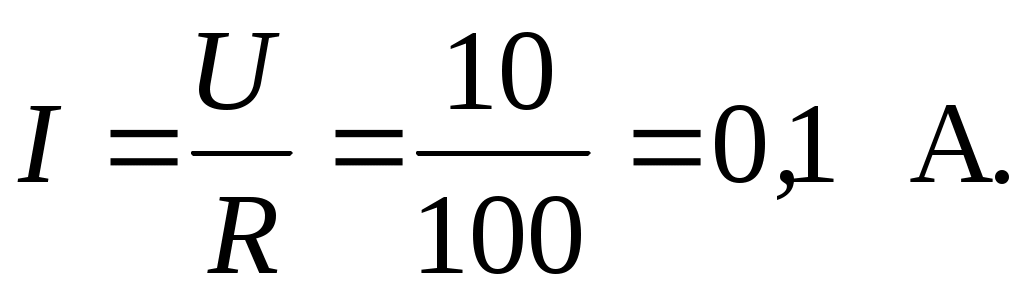

Напряжения: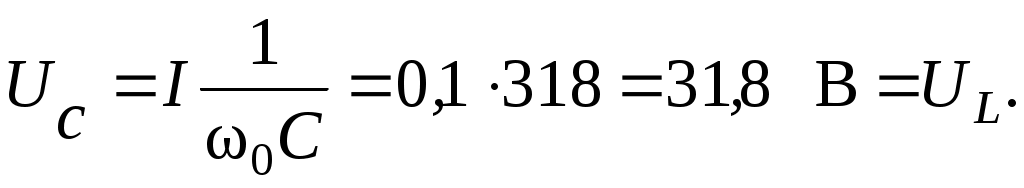





Векторную диаграмму напряжений (рис. 5.4) строим на основании уравнения, составленного по второму закону Кирхгофа:

.

На действительной оси располагаем вектор тока 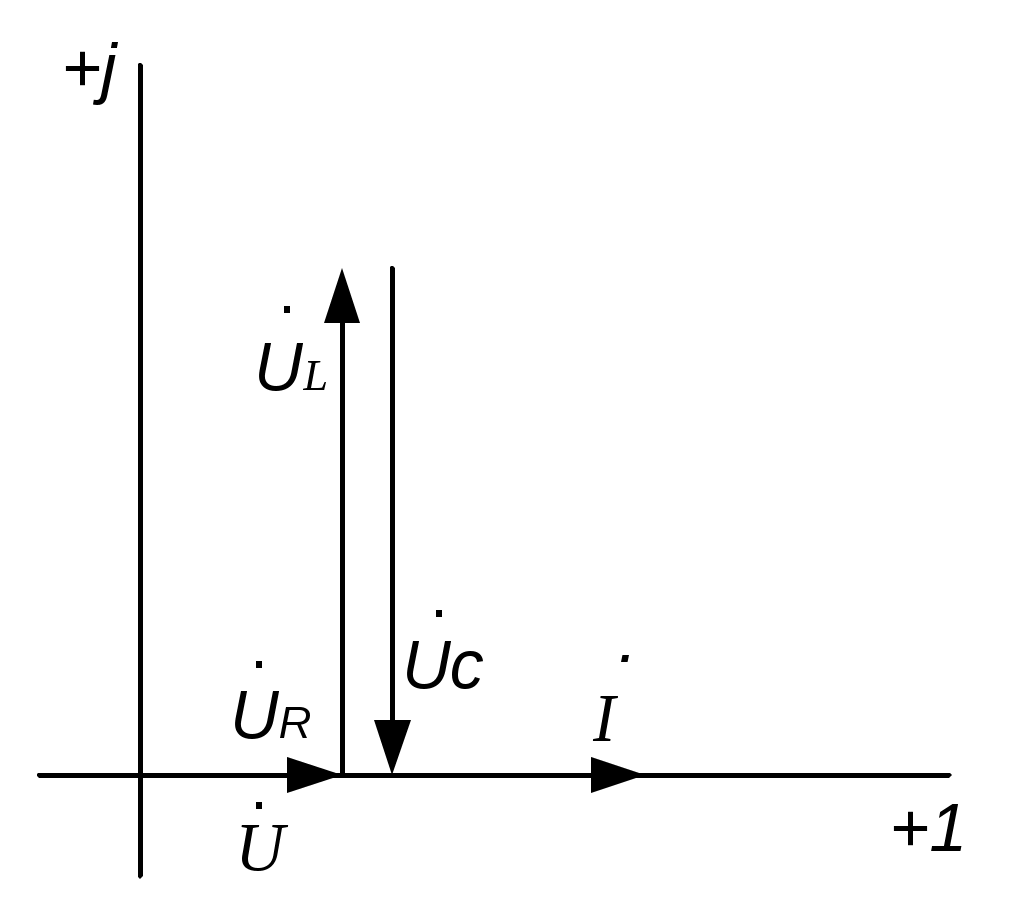как базовый вектор. Вектор напряжения совпадает по фазе с вектором тока , вектор напряжения опережает ток по фазе на 90°, вектор напряжения стает от вектора тока на 90°. Общее комплексное напряжение рав­но сумме комплексных напряжений на элементах R, L, C.



Рис. 5.4

Так как сумма = 0, то .
5.3.2. В электрической цепи (рис. 5.5) R₁ = 80 Ом; R₂ = 60 Ом; L = =0,191 Гн; f = 50 Гц; U = 120 B.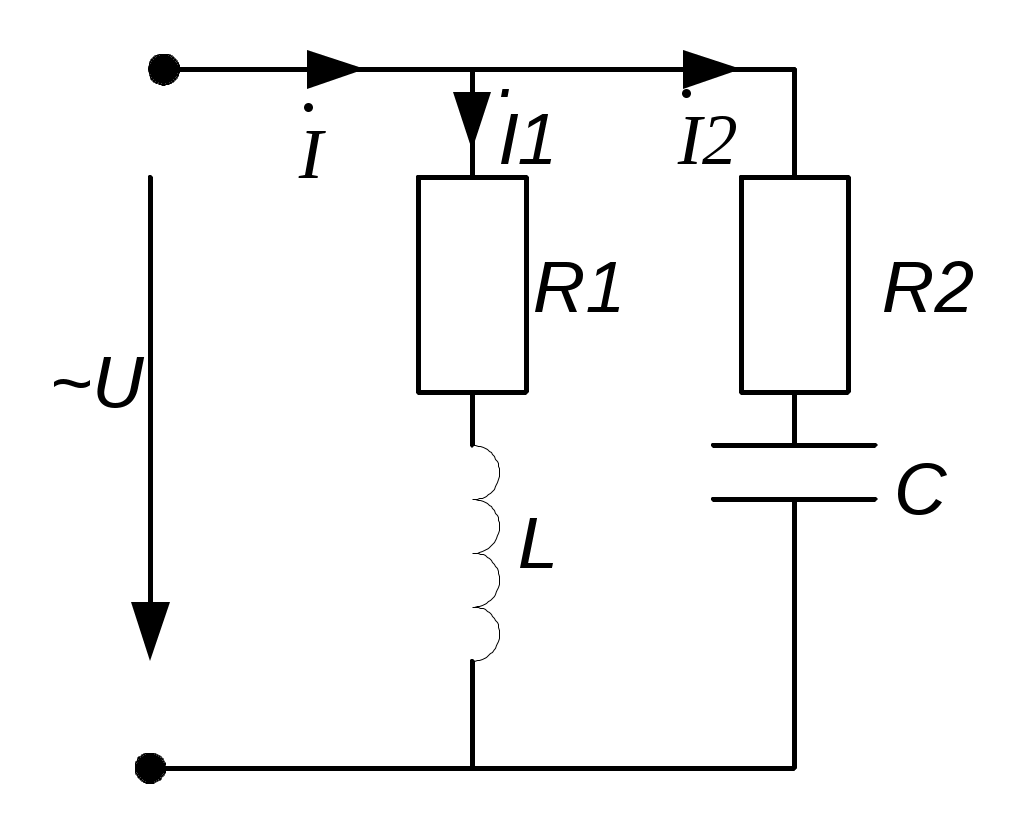



Рис. 5.5
Определить емкость С, при которой наступит резонанс. Рассчитать токи при резонансе и построить векторную диаграмму.

Решение
Условием резонанса токов является равенство b_L=b_С или .

Индуктивное сопротивление

.

Подставим известные величины в уравнение условия резонанса токов

; 0,006 = .

Решаем квадратное уравнение





X_C1 =140,74 Ом, X_C2 =25,86 Ом.

Резонанс токов в заданной схеме возможен при двух разных значениях емкости: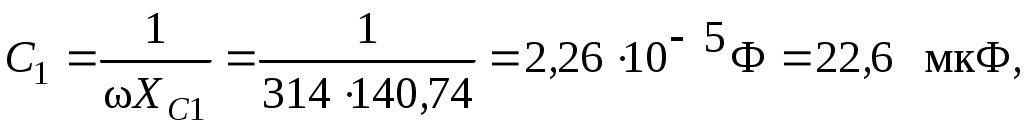





Комплексное сопротивление первой ветви



Комплексное сопротивление второй ветви при С₁ = 22,6 мкФ



при С₂ = 123 мкФ:



Принимаем 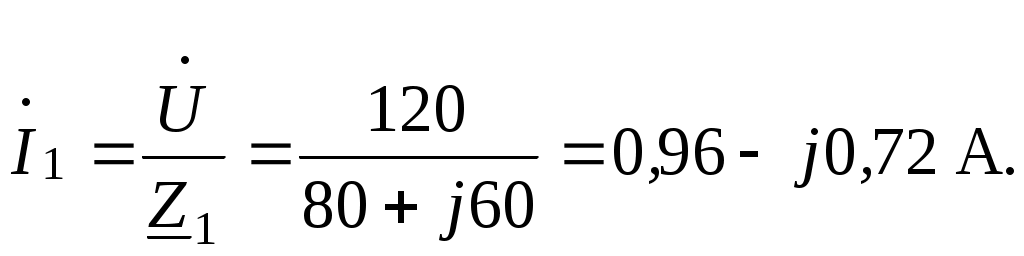тогда ток в ветви с резистором R₁ и индуктивностью L


Действующее значение тока



Ток в ветви с резистором R₂ и емкостью С при X_C1 = 140,74 Ом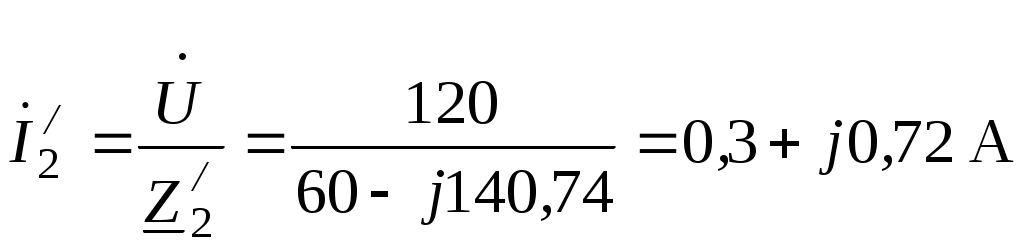

;



Ток в неразветвленной части цепи

=1,26 А.

Получили ток, выраженный в комплексной форме действительным числом, это означает, что ток на входе цепи совпадает по фазе с напряжением, т.е. емкость, при которой наступит резонанс, опреде­лена правильно.

Ток в ветви с резистором R₂ и емкостью С при Х_С2 = 25,86 Ом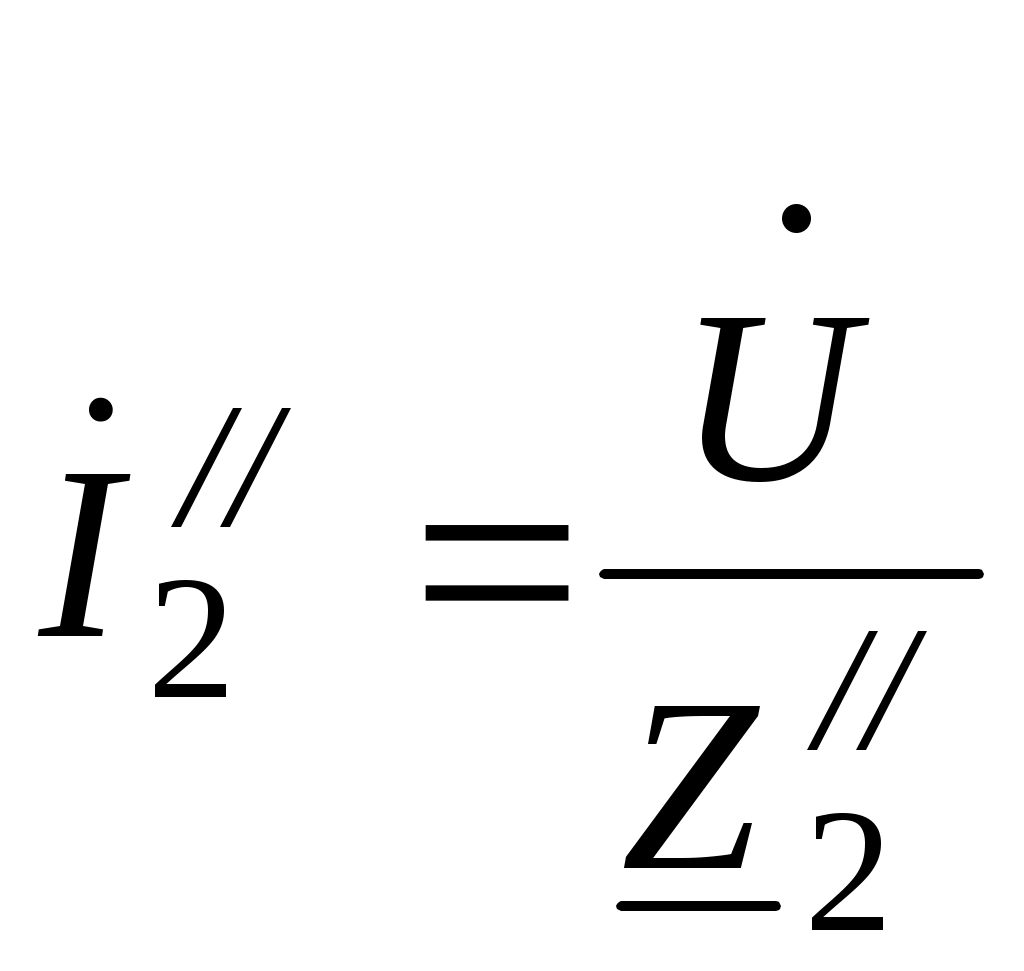





Ток в неразветвленной части цепи



Получили ток, совпадающий с напряжением по фазе. Векторную диаграмму токов (рис. 5.6) строим в масштабе на основании уравнений, составленных по первому закону Кирхгофа для каждого решения.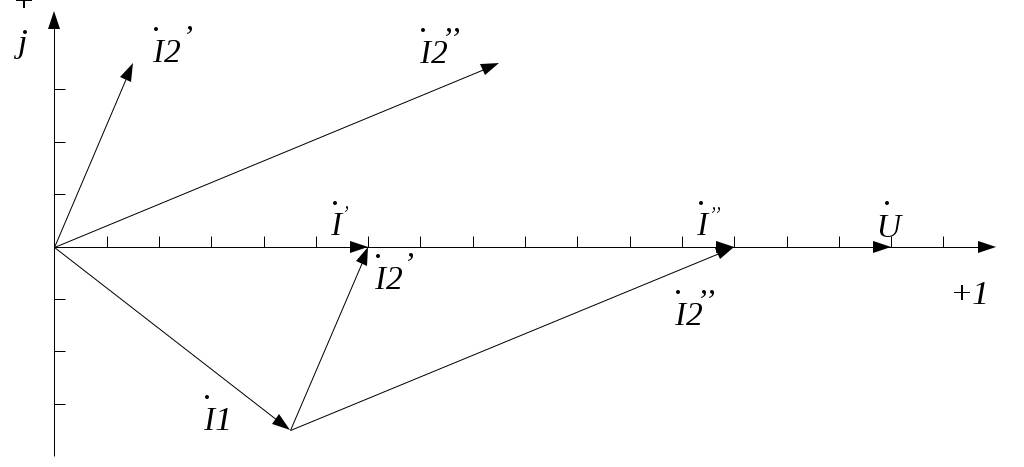

,

.


Рис. 5.6
5.3.3. В электрической цепи (рис. 5.7) U = 30 В; R₁ = 2,7 Ом; X_L = =0,9 Ом; Х_С = 1 Ом.

Определить при каком сопротивлении R₂ в цепи наступит резонанс. Построить векторную диаграмму напряжений и токов.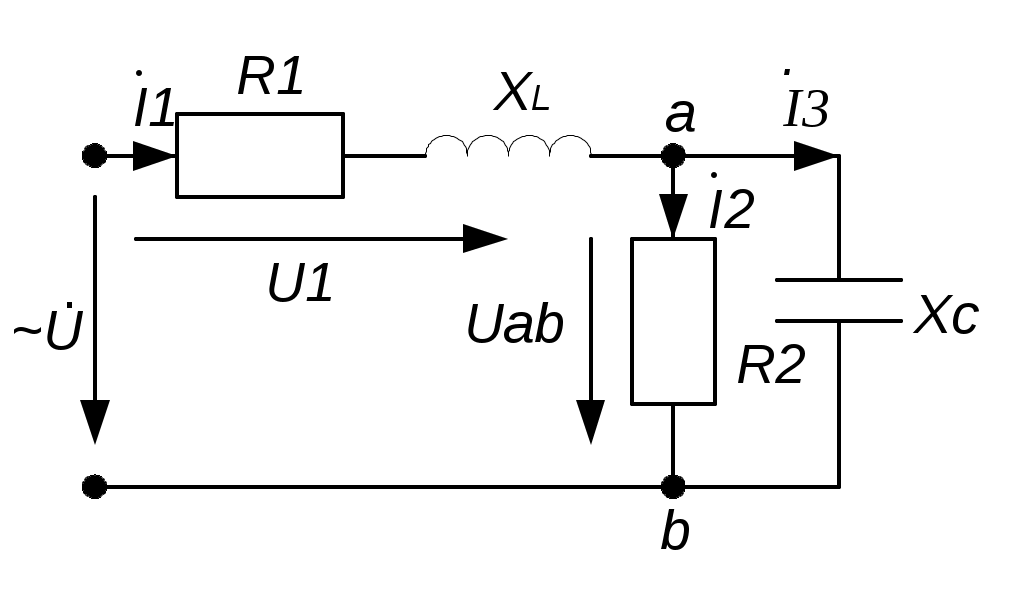


Рис. 5.7
Решение

В цепи рис. 5.7 резонанс наступит при условии, что реактивная составляющая эквивалентного комплексного сопротивления будет равна нулю.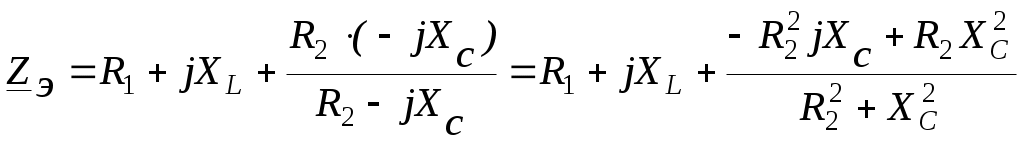

.

Реактивное эквивалентное сопротивление состоит из слагаемых, содержащих множитель j, т. e. это мнимая часть комплексного сопротивления: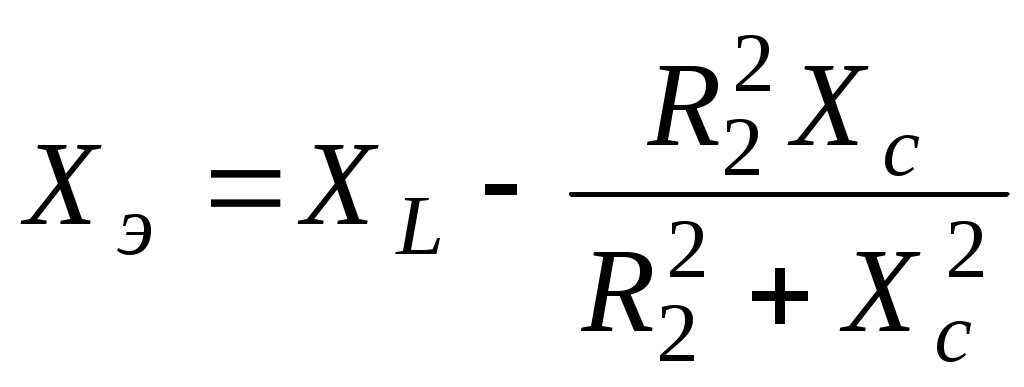

.

Подставляем известные величины и приравниваем Х_э нулю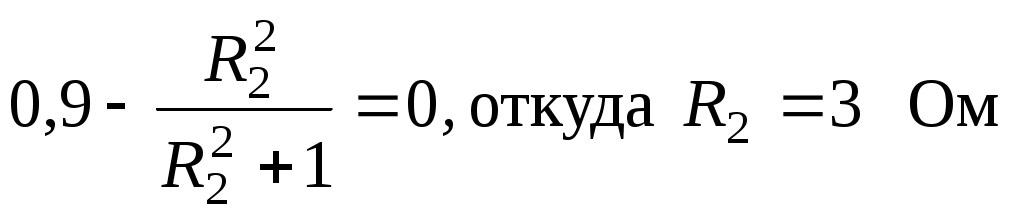

.

При найденном значении R₂ комплексное сопротивление цепи 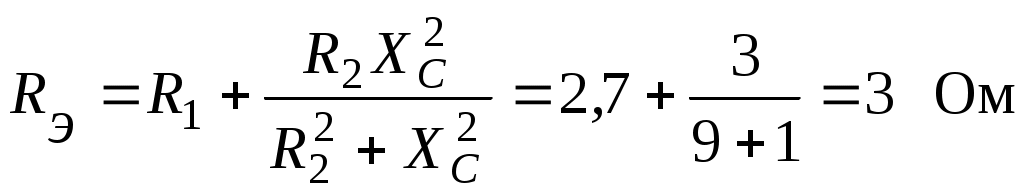имеет только действительную составляющую, т.е. чисто активное сопротивление

.

Принимаем .

Ток в неразветвленной части цепи



Напряжение на участке c параллельным соединением ветвей



Токи в параллельных ветвях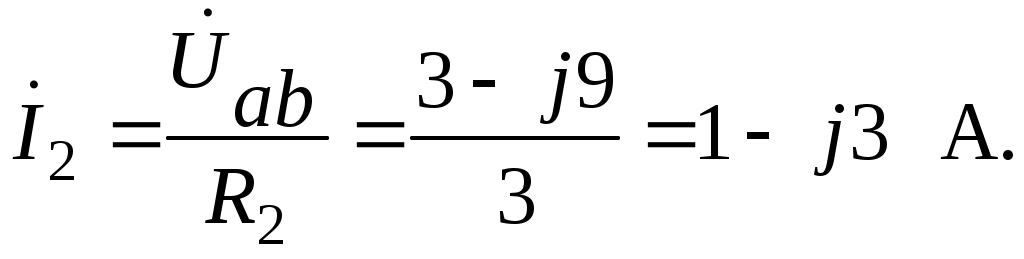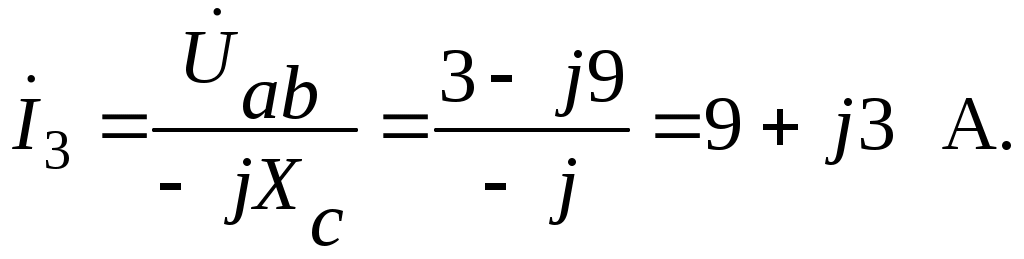





Векторную диаграмму токов и напряжений (рис. 5.8) строим в масштабе на основании уравнений составленных по законам Кирхгофа: 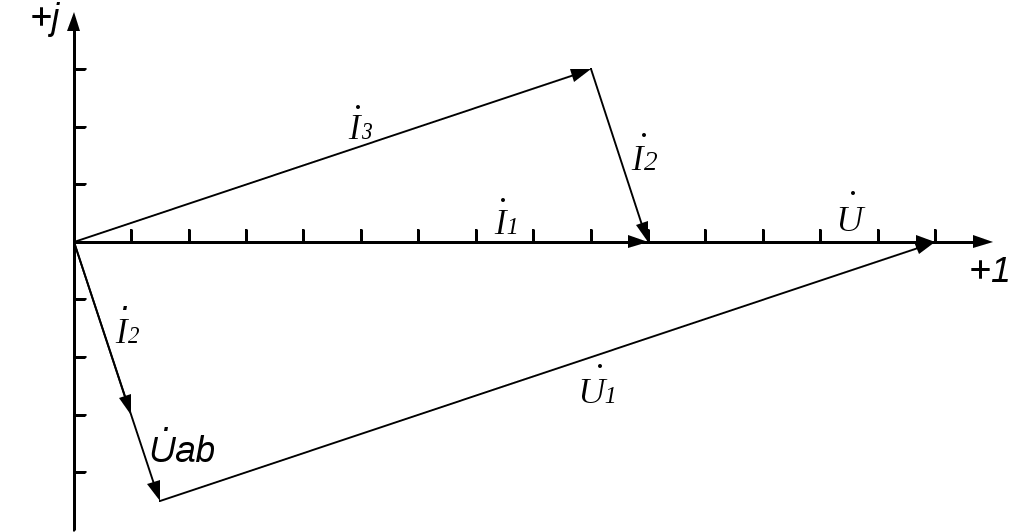Ток на входе цепи I₁ совпадает c напряжением по фазе.



Рис. 5.8

5.4 Задачи для самостоятельного решения
5.4.1. В электрической цепи (рис. 5.9) при частоте 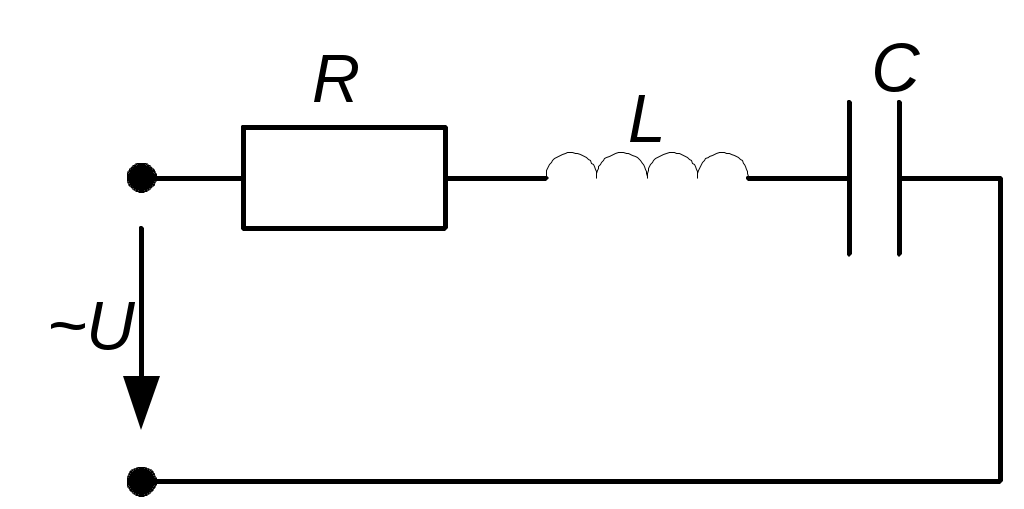имеет место резонанс. Определить R, C, U при Р = 10 Вт; I = 1 A; L = 0,4 Гн. Построить векторную диаграмму напряжений и тока.


Рис. 5.9
Ответ: С = 10 мкФ; R = 10 Ом; U = 10 B.
5.4.2. Приборы в электрической цепи (рис. 5.10) показали

I₁ = 5 А; U = 100 В; Р = 400 Вт.

Определить величину подключа­емой емкости для получения коэффициента мощности всей цепи сos φ = 1, если f = 50 Гц.

Определить токи после включения емкости, построить вектор­ную диаграмму токов и напряжения.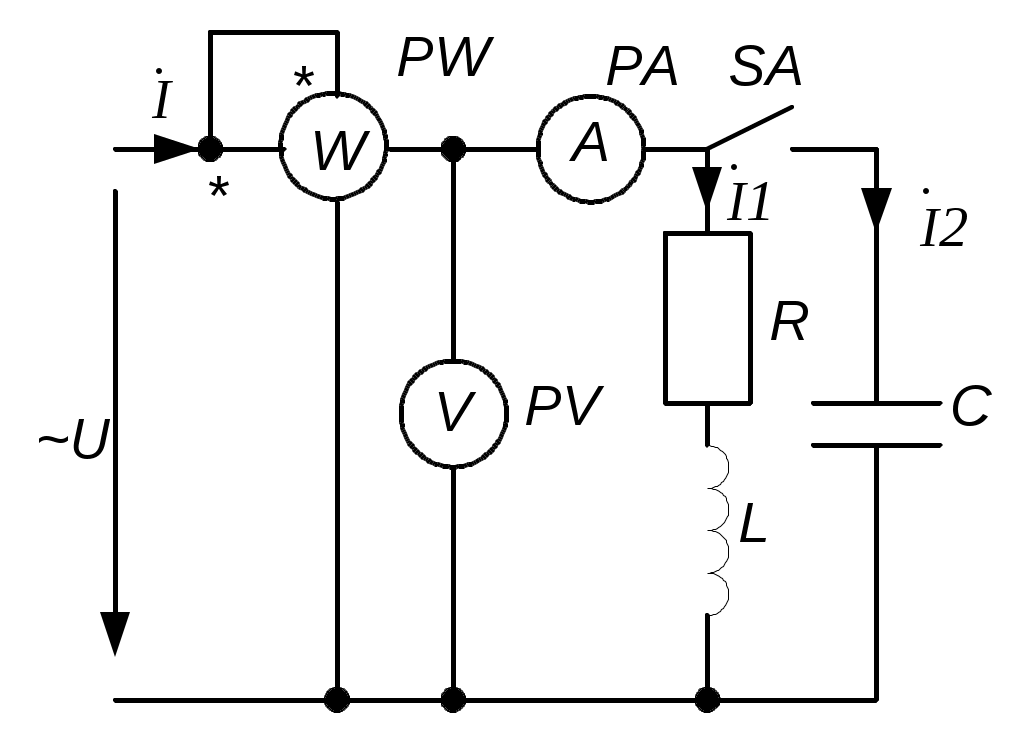



Рис. 5.10
Ответ: С= 95,5мкФ, I = 4 A, I₂ = 3A.

5.4.3. Цепь состоит из индуктивной катушки R, L, соединенной последовательно с конденсатором без потерь. Приложенное ко всей цепи напряжение U = 35 В.Определить напряжение на катушке при резонансе, если при этом напряжение на конденсаторе равно 120 В. Ответ: 125 В.
5.5 Индивидуальные задания

В электрических цепях (рис. 5.11...5.16) имеет место резонанс. Действующее значение синусоидального напряжения источника питания U = 100 В. По данным таблицы 5.1. определить величину, указанную в крайнем правом столбце, токи и напряжения на участках цепи, построить векторную диаграмму напряжений и токов.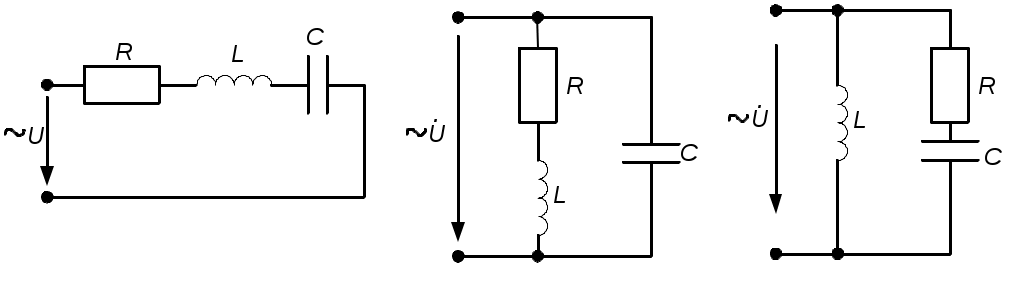


Рис. 5.11 Рис. 5.12 Рис. 5.13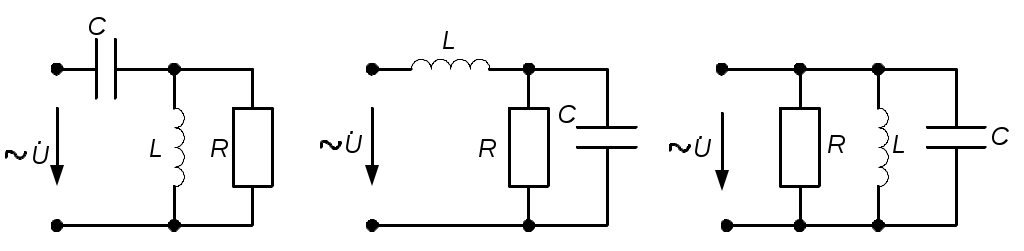


Рис. 5.14 Рис. 5.15 Рис. 5.16
Таблица 5.1.

№ вар.	№ схемы	R, Ом	XL, Ом	ХС, Ом	ω, рад/с	L, мГн	С, мкФ	Опре – делить
1	5.11	5	–	–	–	10	100	f
2	5.12	10	10	–	–	–	–	ХС
3	5.13	20	–	20	100	–	–	L
4	5.14	20	–	10	–	–	–	XL
5	5.15	10	–	20	–	–	–	XL
6	5.16	10	–	–	1000	20	–	С
7	5.11	40	–	–	500	400	–	С
8	5.12	20	10	–	–	–	–	ХС
9	5.13	10	–	10	–	–	–	XL
10	5.14	20	10	–	200	–	–	С
11	5.15	10	–	10	–	–	–	XL
12	5.16	20	–	–	–	20	50	ω
13	5.11	50	–	–	1000	–	10	L
14	5.12	10	30	–	–	–	–	ХС
15	5.13	30	–	30	–	–	–	XL
16	5.14	3	4	–	–	–	–	ХС
17	5.15	8	–	6	–	–	–	XL
18	5.16	40	–	–	500	–	200	L

5.6 Контрольные вопросы

1. 
   Дайте определение резонансного режима работы двухполюсника.
   
2. 
   Запишите условие резонансного режима работы двухполюсника.
   
3. 
   При каком условии наступает резонанс напряжений?
   
4. 
   Чему равна и что показывает добротность последователь­ного контура?
   
5. 
   В каких цепях и при каком условии наступает резонанс токов?
   
6. 
   Что называется компенсацией сдвига фаз?
   
7. 
   Докажите с помощью схемы и векторной диаграммы, что с помощью параллельно включенного конденсатора можно достичь компенсации сдвига фаз.