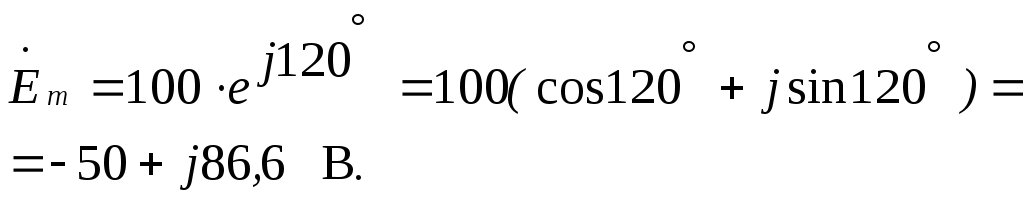Электрических цепей постоянного тока

• Название: Электрических цепей постоянного тока
• Дата: 23.07.2022
• Размер: 5.4 Mb.
• Имя файла: materialy-dlya-dlya-studentov-fakulteta-elektrifikacii-po-podgot.doc
• Тип: Закон; #635135
• страница: 4 из 8

Тема 2

СИНУСОИДАЛЬНЫЙ ТОК. ИЗОБРАЖЕНИЕ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН ВЕКТОРАМИ И КОМПЛЕКСНЫМИ ЧИСЛАМИ. РАСЧЕТ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

Цель: Усвоить основные понятия и величины, характеризующие переменный синусоидальный ток. Овладеть методами представления его векторами и комплексными числами, комплексным методом расчёта цепей синусоидального тока при последовательном соединении элементов R, L, C. Освоить методику расчета цепей синусоидального тока со смешанным соединением приемников.

2.1 Задания по самоподготовке

1. Проработать по учебникам и учебным пособиям тему «Электрические цепи синусоидального тока» [1] §.3.1, 3.2, 3.4, 3.5, 3.7, 3.8, 3.9, 3.11, 3.12, 3.14, 3.16, 3.18 и [4] § 3.8, 3.9, 3.10.

2. Повторить тему “Комплексные числа. Действия над комплексными числами” (см. при­ложение А), методику расчета цепей постоянного тока со смешанным соединением резисторов.

3. Разобрать примеры из раздела 2.3.

4.Ответить на контрольные вопросы.

2.2 Общие сведения

Переменным называют ток, изменяющийся во времени. Переменный ток, который описывается синусоидальной функцией, называется синусоидальным током. Важно усвоить основ­ные понятия и величины, характеризующие синусоидальный ток: период, частота, амплитуда, угловая (циклическая) частота, фаза, начальная фаза.

Периодом называется время одного полного колебания. Период обозначается латинской буквой Т и измеряется в секундах (с). Величина, обратная пе­риоду Т, т.е. число периодов в единицу времени, называется частотой, обо­значается f и измеряется в герцах (Гц):



На рис. 2.1 изображен график синусоидального тока, построенный согласно математическому выражению его мгновенного значения, которое имеет вид ,

где i  –  мгновенное значение тока;

I_m – максимальное значение или амплитуда тока;

• 
  –  угловая (циклическая) частота, w = 2pf, измеряется в радианах в секунду (рад/с);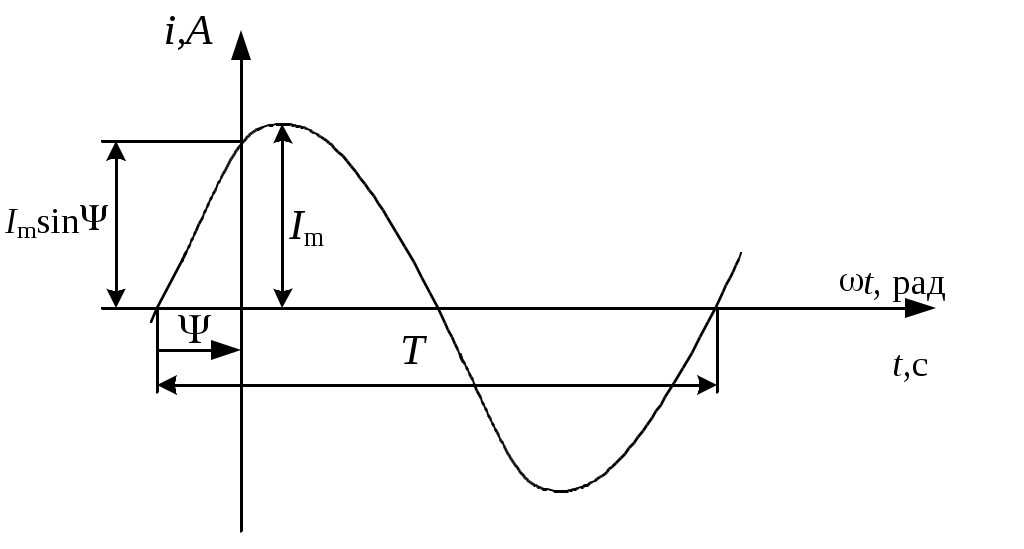
  

–  начальная фаза, определяемая смещением начала синусоиды относительно начала координат (началом синусоиды считается точка пере­хода отрицательной полуволны в положительную).



Рис. 2.1

Следует обратить внимание, что угол y положителен в том случае, если начало синусоиды смещено влево от начала координат, и, наоборот, угол y отрицателен, если начало синусоиды смещено вправо от начала ко­ординат.

Величина (wt + y), определяющая стадию изменения синусоидаль­ной функции, называется фазовым углом или фазой.

При расчете цепей синусоидального тока наряду с амплитудным значением тока широко используется понятие действующего значения тока. Действующие значения синусоидального тока, напряжения, ЭДС свя­заны с их амплитудными значениями соотношениями:



Для облегчения расчетов и анализа цепей синусоидального тока ши­роко применяется метод представления синусоидальных функций век­торами и комплексными числами. Сущность метода заключается в том, что синусоидальной вели­чине ставится в соответствие вектор на комплексной плоскости. Длина вектора (модуль) равна амплитуде синусоидальной величины. Вектор строится выходящим из начала координат под углом y к действительной положительной полуоси комплексной плоскости. Если y > 0, вектор повернут против часовой стрелки, если y < 0, то вектор повернут по часовой стрелке.

В свою очередь данный вектор может быть аналитически представ­лен комплексным числом, которое получило название комплексной амплитуды.

Комплексную амплитуду, как и любое комплексное число, можно записать в показательной, тригонометрической и алгебраической формах.

Удобнее всего, при переходе от синусоидальной функции к записи её комплексной амплитуды, пользоваться показательной формой. При этом модуль комплексного числа берётся равным амплитуде синусоидальной величины, а аргумент - углу y. Если комплексную амплитуду разделить на 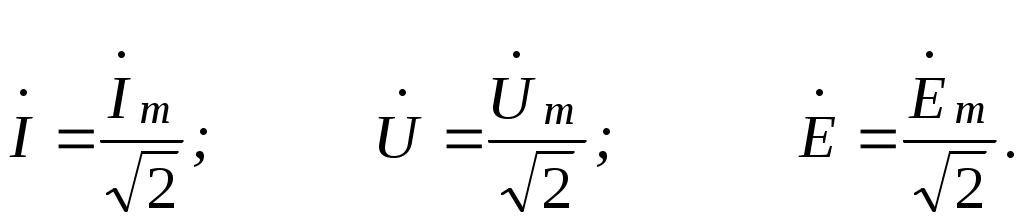, то получим комплексное действующее значение синусоидальной величины:



Имея комплексную амплитуду или комплексное действующее значение, можно осуществить обратный переход и записать выражение мгновенного значения соответствующей синусоидальной величины.

Расчет цепей синусоидального тока, состоящей из последовательно соединённых элементов R, L и C (рис. 2.2), основывается на законе Ома в комплексной форме.

Закон Ома в комплексной форме:

(2.1)

где  –  комплексные действующие значения тока и напряжения;

Z – комплексное сопротивление.

Для цепи с последовательным соединением элементов R, L, C (рис. 2.2) комплексное сопротивление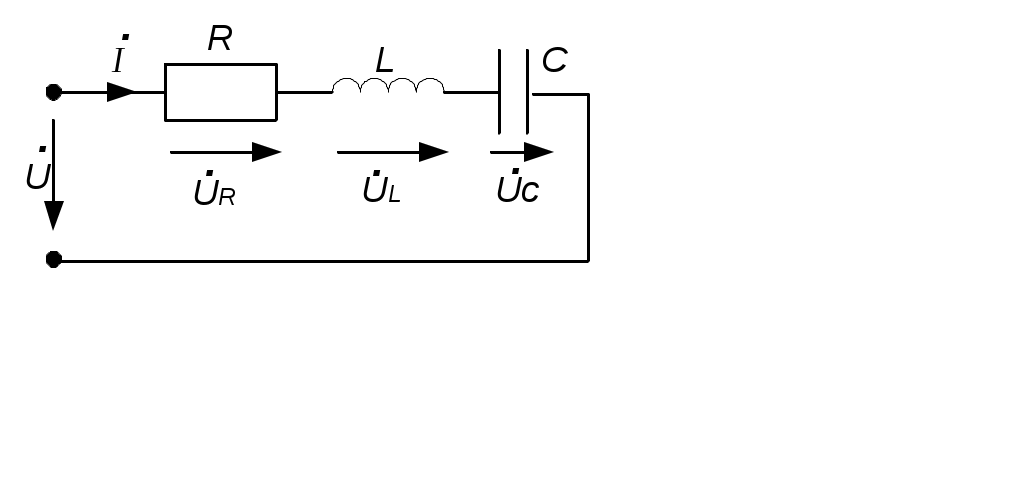

. (2.2)



Рис. 2.2

Закон Ома принимает вид: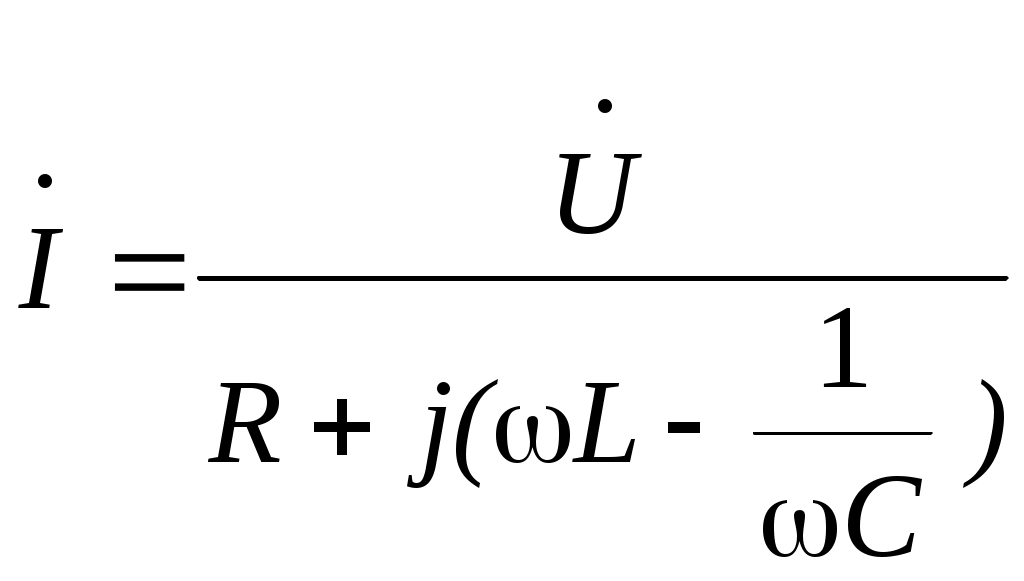

(2.3)

Введем обозначения:

 –  индуктивное сопротивление,

 –  емкостное сопротивление.

Закон Ома принимает вид: 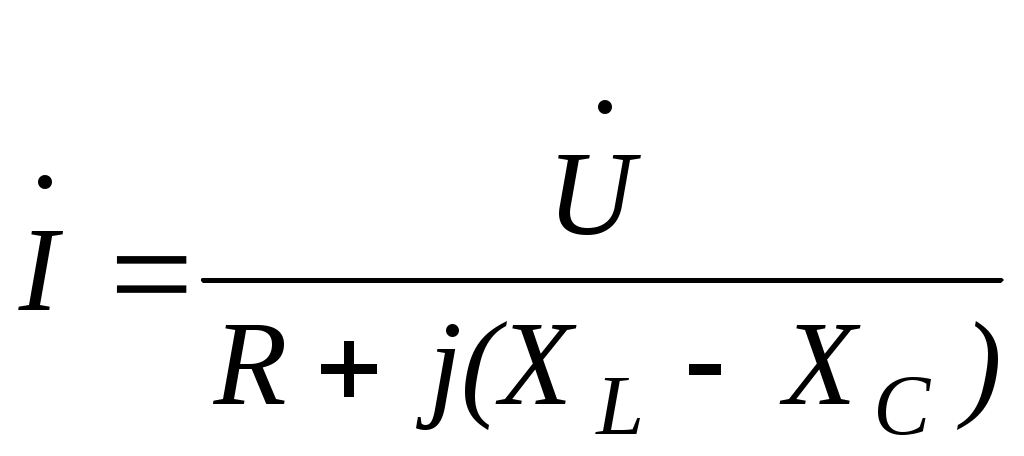. (2.4)

Введем обозначение:

X_L – X_C = X – реактивное сопротивление.

Тогда комплексное сопротивление Z = R + jX.

Комплексное сопротивление может быть записано в показательной форме: Z = Z ,

где  –  модуль комплексного сопротивления, называется полным сопротивлением,

 –  аргумент (угол) комплексного сопротивления.

Из закона Ома в комплексной форме комплексное сопротивление

Z =  .

Записав комплексные величины в показательной форме, получим:

.

Следовательно .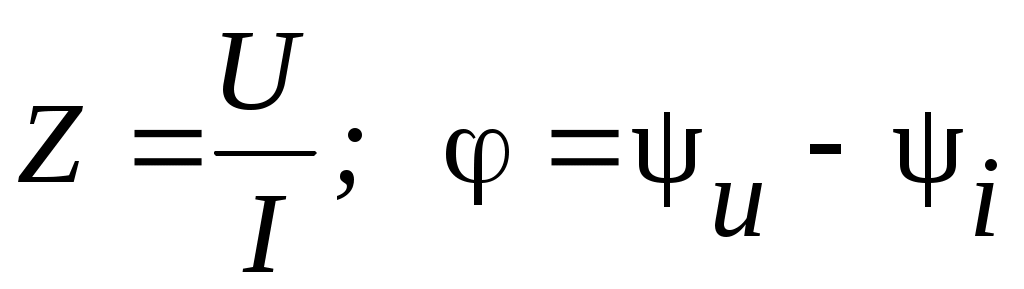

Полное сопротивление Z, активное сопротивления R и реактивное сопротивление X соотносятся между собой как стороны прямоугольного треугольника, который получил название треугольника сопротивлений. В треугольнике Z – гипотенуза, R– прилегающий к углу 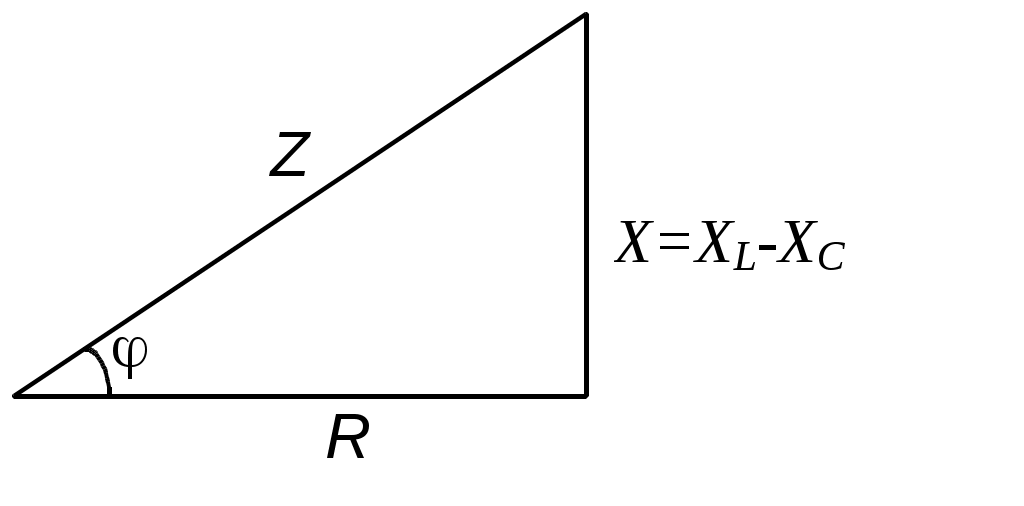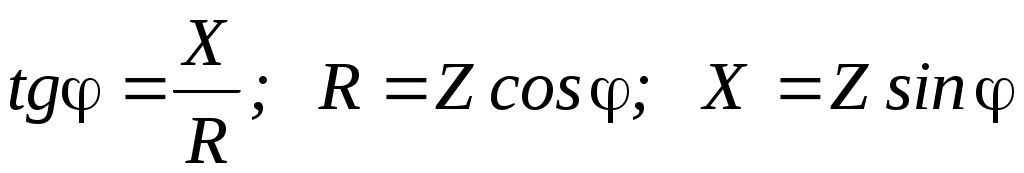катет. Из этого треугольника .

Для ветвей электрической цепи, каждая из которых содержит только сопротивление R, только индуктивность L и только емкость С, комплексные сопротивления соответственно равны:

Z_R = R; Z_L = jωL; Z_C =  .

Если ветвь содержит не по одному элементу R, L и С, включенных последовательно, а несколько, то вначале определяют эквивалентное активное сопротивление

R_экв = R₁ + R₂ + … + R_n,

эквивалентное индуктивное сопротивление

X_Lэкв = X_L1 + X_L2 + … + X_Lk,

эквивалентное емкостное сопротивление

X_Cэкв = X_C1 + X_C2 + … + X_Cm,

а затем, в соответствии с рис.2.3 находят комплексное сопротивление

Z = R_экв + j(X_Lэкв – X_Cэкв);

Для наглядности расчет цепи часто сопровождают построением векторной диаграммы тока и напряжений. При построении диаграммы необходимо помнить, что на резистивном элементе напряжение и ток совпадают по фазе, на индуктивном элементе напряжение опережает ток на угол 90º, на емкостном элементе напряжение отстает от тока на угол 90º. По этой причине 2-й закон Кирхгофа для схемы рис. 2.2 выполняется только для комплексных значений напряжений и не выполняется для действующих значений:

; .

Методика расчета цепей синусоидального тока со смешанным соединением аналогична методике расчета цепей постоянного тока со смешанным соединением. Отличие заключается лишь в том, что расчет проводится в комплексной форме.
2.3. Примеры

2.3.1. Задано выражение мгновенного значения синусоидального тока: А. Определить: амплитуду тока I_m, действующее значение I, период Т, частоту f, угловую частоту w, начальную фазу y.

Решение

I_m = 10 A;

I =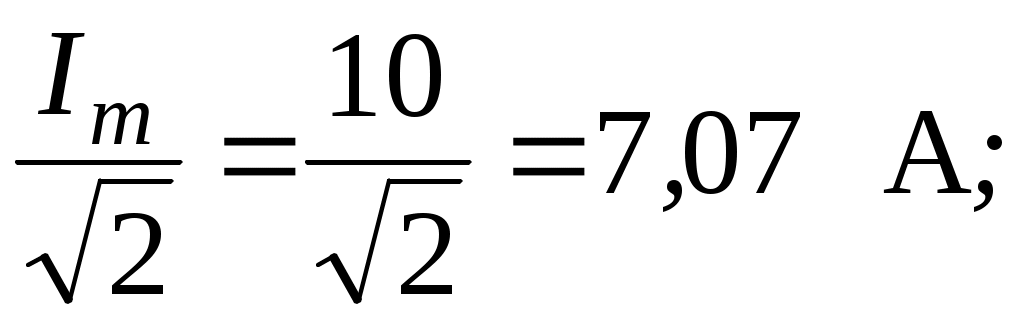 

w = 314

w = 2pf;

f =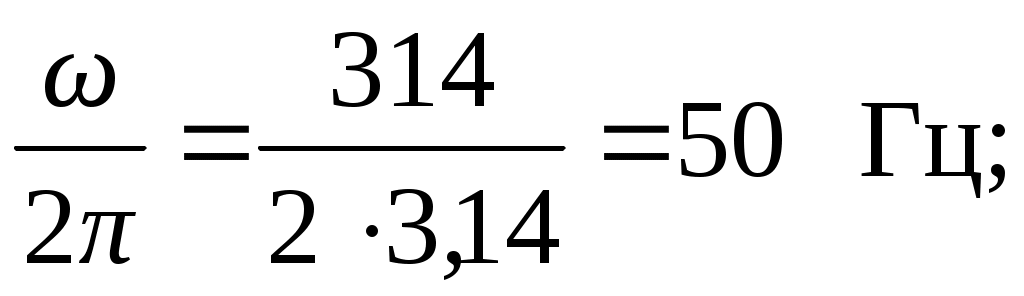 

T =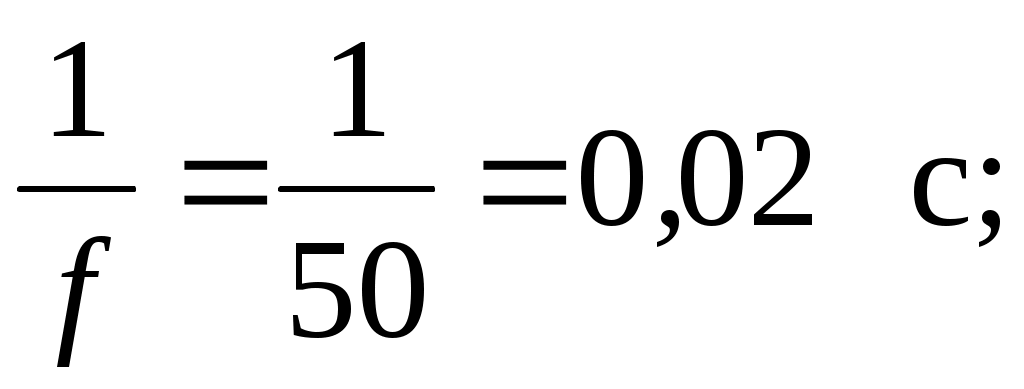 

Y = 60°.

2.3.2. Задано мгновенное значение синусоидальной ЭДС В. Построить на комплексной плоскости вектор, изображающий эту ЭДС и записать ее комплексную амплитуду.

Решение

Рис. 2.3

Строим на комплексной плоскости вектор , длина которого в масштабе равна 100В, направленный под углом y = 120° к действительной положительной полуоси (рис. 2.3). Записываем его комплексную амплитуду

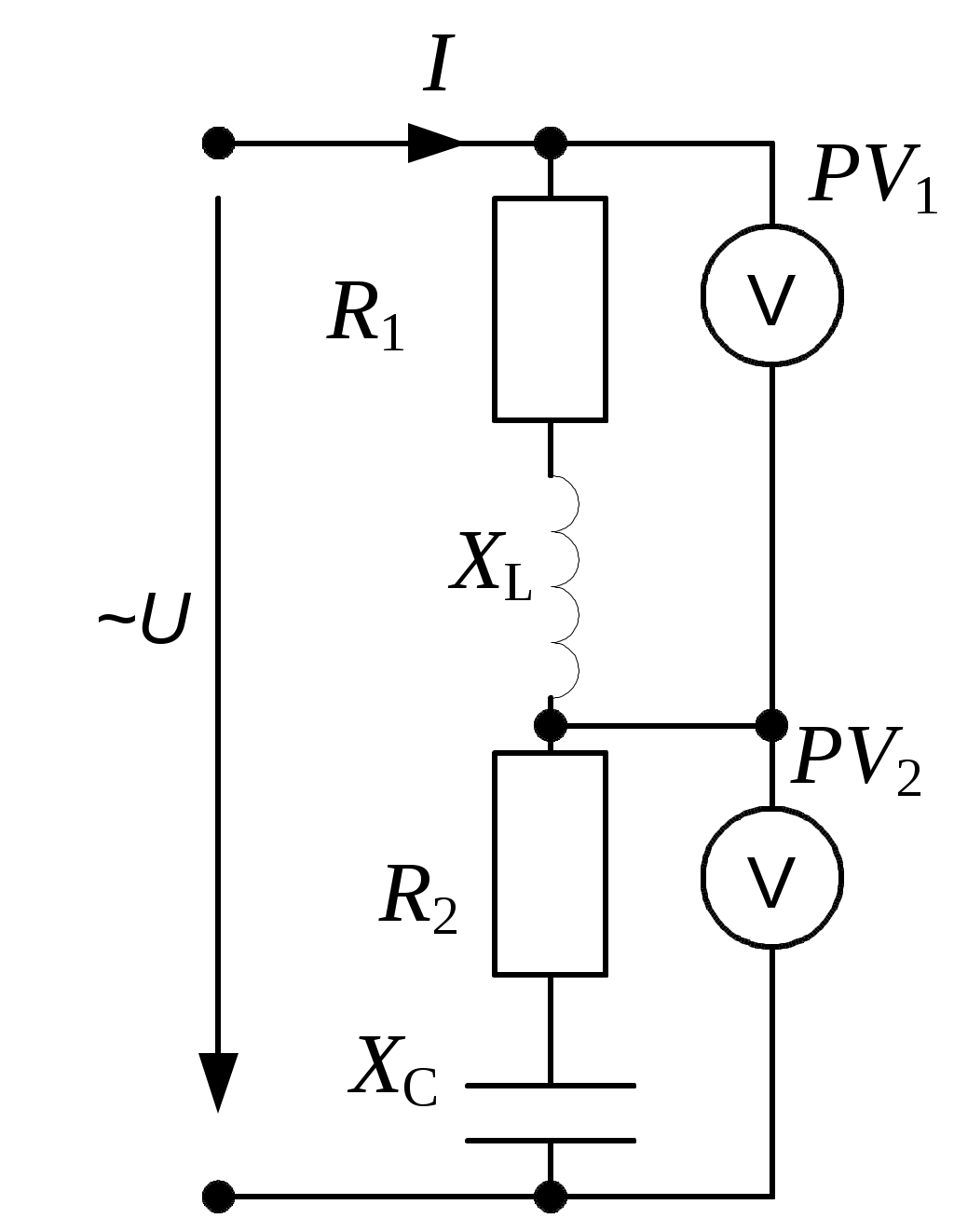
2.3.3. Задано комплексное действующее значение тока . Записать выражение его мгновенного значения.

Решение

Определяем действующее значение тока, как модуль комплексного действующего значения тока:

.

Определяем амплитуду тока, умножая действующее значение на :

.

Определяем начальную фазу, как арктангенс отношения величины мнимой части комплексного значения тока к вещественной части:

.

Записываем выражение мгновенного значения синусоидального тока



Замечание: При определении угла y следует иметь в виду, что арктангенс отношения мнимой части комплексного числа к его вещественной части даст истинное значение угла в том случае, если вектор находится в первом или четвертом квадранте.

Если же вектор расположен во втором либо третьем квадранте, то к полученному значению угла необходимо прибавить 180°.

Чтобы избежать ошибки, рекомендуется оценить величину угла, построив предварительно вектор на комплексной плоскости.

2.3.4. Определить действующие ток и напряжения на элементах цепи (рис.2.4,) если: R = 30 Ом; L₁ = 80 мГн; L₂ = 20 мГн;C = 16,7 мкФ;

u = 141sin1000t B. Построить векторные диаграммы тока и напряжений. Задачу решить комплексным методом.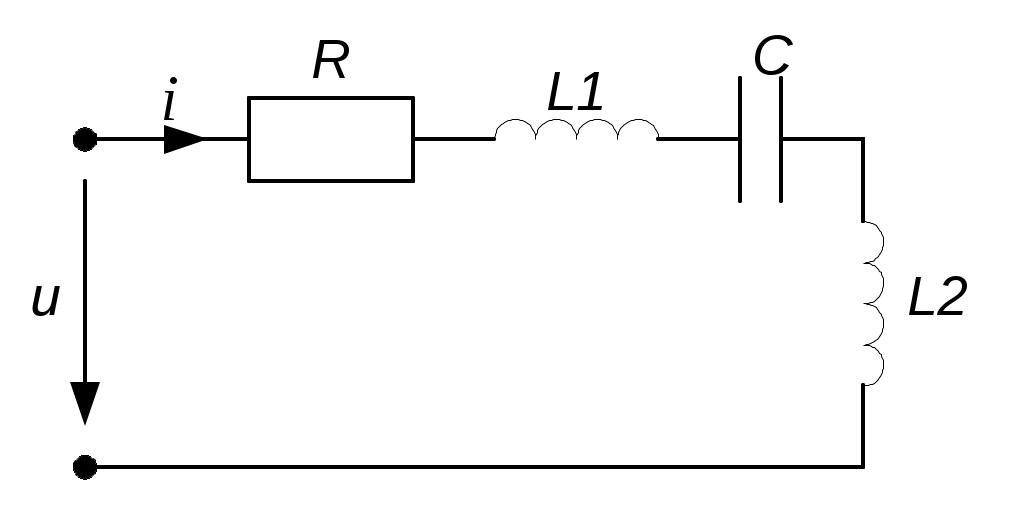




Рис. 2.4
Решение

Определяем индуктивные и емкостные сопротивления

X_L1 = ωL₁ = 1000·0,08 = 80 Ом;

X_L2 = ωL₂ = 1000·0,02 = 20 Ом;

Ом.

Комплексное сопротивление цепи при последовательном соединении элементов

Z = R + j(X_L1 + X_L2-X_C) = 30 + j(80 + 20-60) = 30 + j40 Ом.

Запишем комплексное действующее напряжение на входе цепи:

В.

По закону Ома в комплексной форме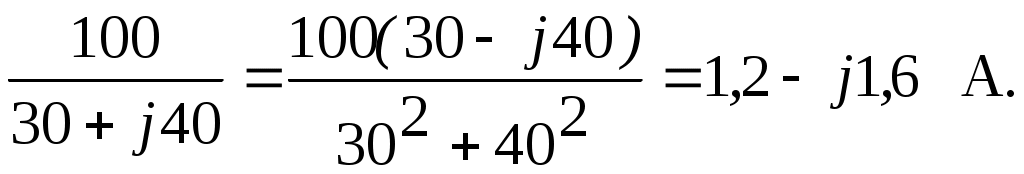

/Z = 

Действующее значение тока

Напряжения на элементах цепи находим по закону Ома

Z_R

Действующее напряжение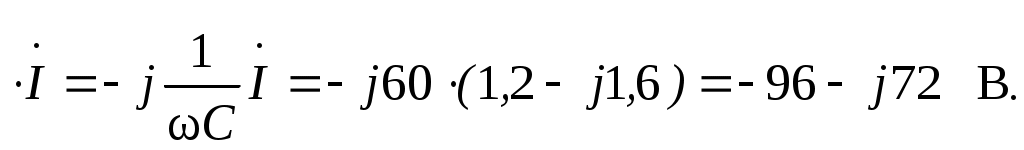

Z_L1·



Z_L2



Z_C



Проверка по второму закону Кирхгофа в комплексной форме: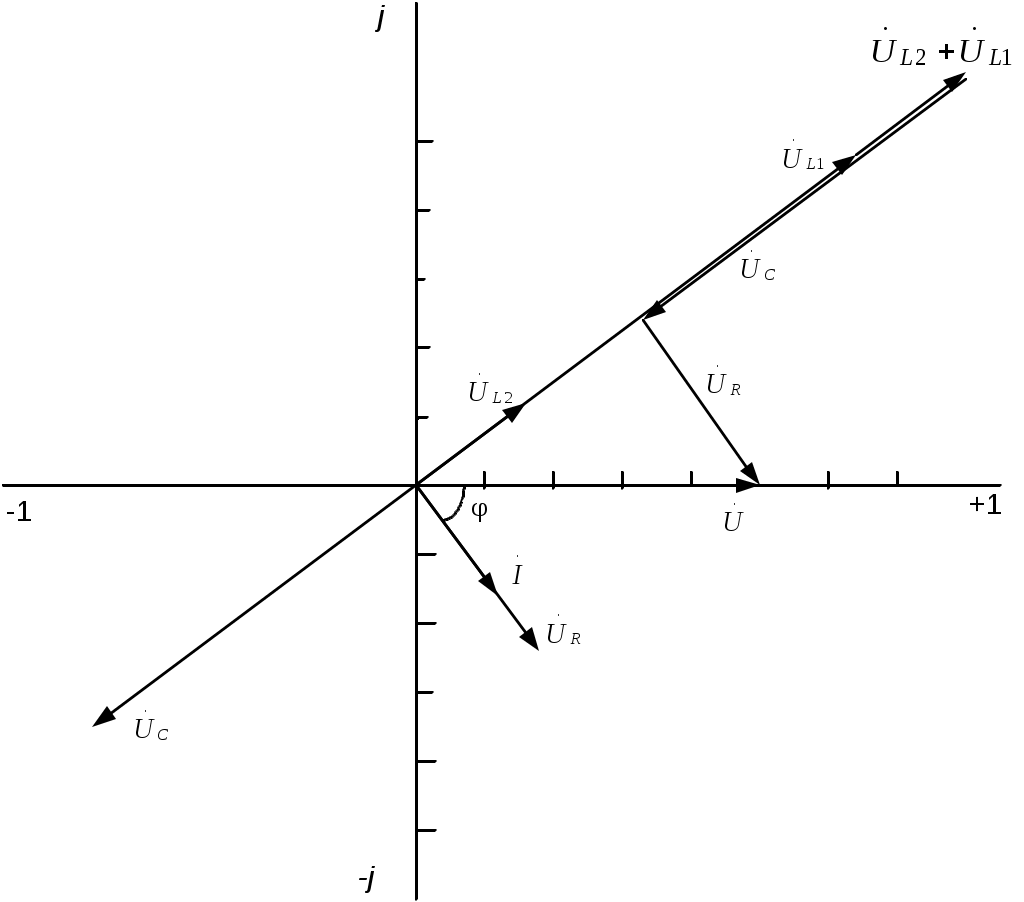

Векторную диаграмму строят в соответствии с расчетом в комплексной форме. Векторы тока и напряжений располагают в одной комплексной плоскости. Выбирают масштабы построения векторов.


Рис. 2.5

Как видим, на векторной диаграмме (рис. 2.5) векторы напряжений на индуктивных элементах опережают вектор тока на 90^˚ (повернуты по отношению к вектору на 90^˚ против часовой стрелки). Вектор напряжения отстает от вектора на 90˚ (повернут по отношению к вектору на 90˚ по часовой стрелке), а вектор напряжения на активном сопротивлении совпадает с вектором тока . Складывая векторы напряжения на элементах цепи, получаем напряжение на входе цепи

2.3.5. Определить показания вольтметров PV₁ и PV₂, в схеме (рис.2.6), если: U = 120 В; R₁ = 50 Ом; R₂ = 10 Ом; X_L = 50 Ом; X_C = 30 Ом.

Рис. 2.6

Решение Примем начальную фазу напряжения Ψu = 0, тогда Комплексные сопротивления участков цепи: Z1 = R1 + jXL = 10 + j50 Ом; Z2 = R2 – jXC = 10 -j30 Ом.

Комплексное сопротивление всей цепи

Z = Z₁ + Z₂ = 10 + j50 + 10 - j30 = 20 + j20 Ом.

По закону Ома ток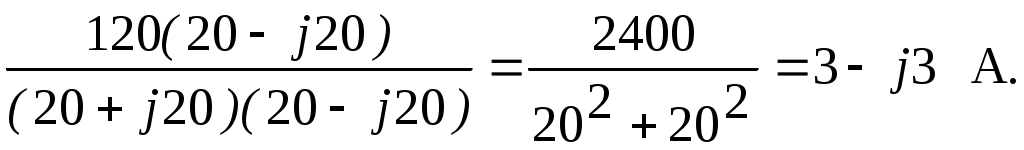

/Z = 

Падения напряжений на отдельных участках цепи:

Z₁

Z₂

Действующие значения напряжений:





2 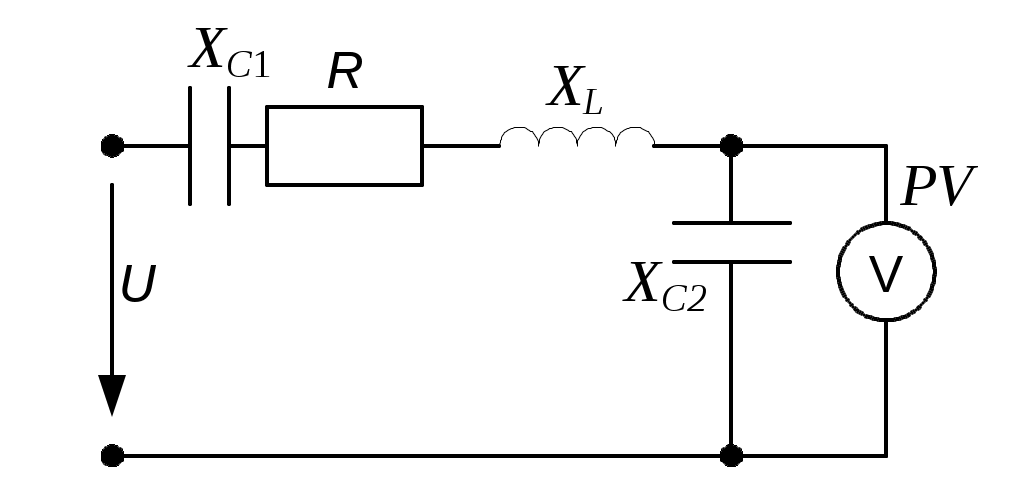.3.6. Определить ток, напряжение на входе цепи (рис. 2.7) и напряжения на элементах, если вольтметр PV показывает 60 В.

R = 50;

X_L = 100;

X_C1 = 50;

Рис. 2.7 X_C2 = 20.

Построить векторную диаграмму тока и напряжений.

Решение

Поскольку все элементы цепи включены последовательно, то по ним протекает один и тот же ток. Величину тока определим по закону Ома в комплексной форме для участка цепи с сопротивлением X_C2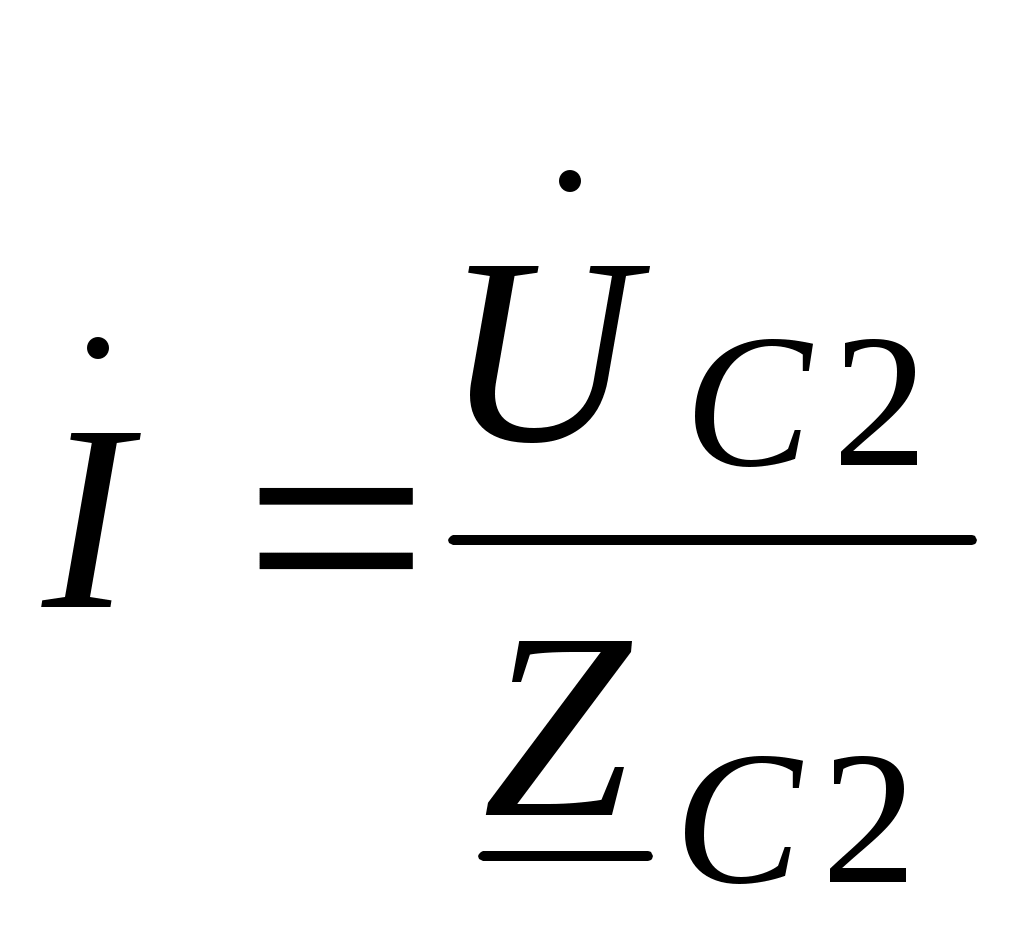

.

Принимаем: .

Z_C2 =  -jX_C2 =  -j20 Ом.

.

Действующий ток I = 3 А.

Комплексное сопротивление цепи при последовательном соединении элементов

Z = R + j(X_L-X_C1-X_C2) = 40 + j(100-50-20) = 40 + j30 Ом.

Напряжение на входе цепи

Z  = (40 + j30) j3 =  - 90 + j120 В.

Действующее значение напряжения

.

Определим напряжения на элементах цепи по закону Ома в комплексной форме

_R = Z_R  = 40 · j3 = 120j В,

_C1 = Z_C1  =  -j50 · j3 = 150 В,

_L = Z_L  = j100 · j3 =  - 300 В.

Действующие напряжения на элементах цепи:

_R = 120 В, _C1 = 150 В, _L = 300 В.

Проверка по второму закону Кирхгофа в комплексной форме

 =  _R +  _C1 +  _C2 +  _L  = 150 + j120-300 + 60 =  -90 + j120 В.

Строим векторную диаграмму (рис. 2.8)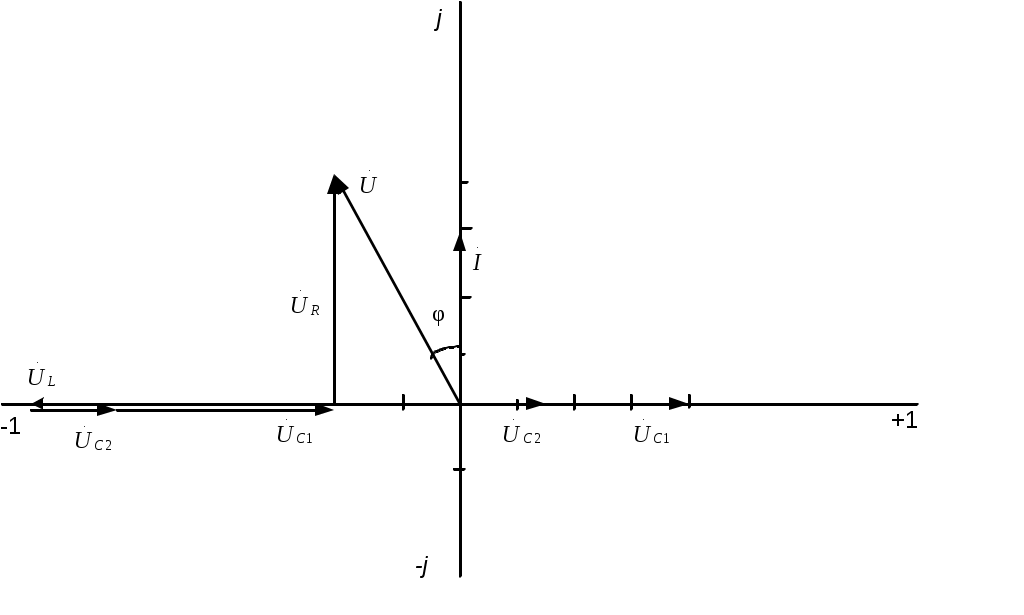



Рис. 2.8

2.3.7. Определить токи в цепи (рис. 2.9) и построить векторную диаграмму токов и напряжений.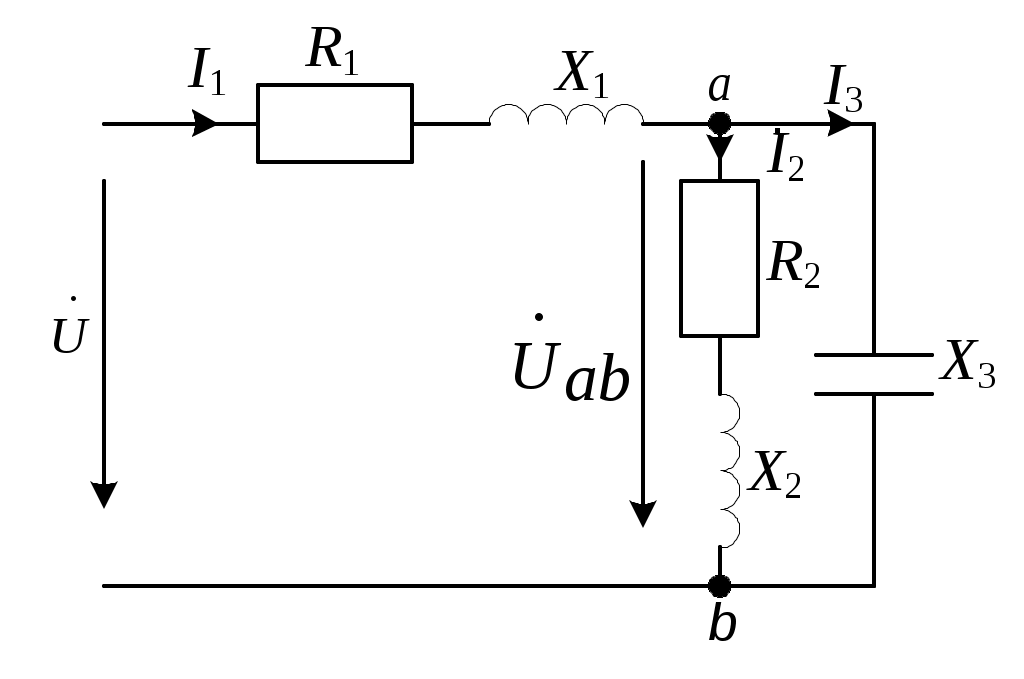

R₁ = 8 Ом; X₁ = 6 Ом;

R₂ = 3 Ом; X₂ = 4 Ом;

X₃ = 10 Ом; U = 40 B.

Рис. 2.9

Решение

Принимаем начальную фазу напряжения Ψ_u = 0, тогда В. записываем комплексные сопротивления ветвей:

Z₁ = R₁ + jX₁ = 8 + j6 Ом;

Z₂ = R₂ + jX₂ = 3 + j4 Ом;

Z₃ =  -jX₃ =  -j10 Ом.

Определяем эквивалентное комплексное сопротивления всей цепи:

Z₂ и Z₃ соединены параллельно, поэтому

Z₂₃ = Z₂·Z₃/(Z₂ + Z₃) =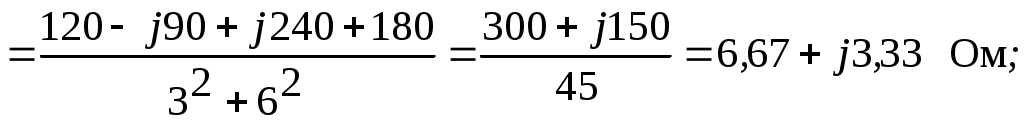 



Z₂₃ и Z₁ соединены последовательно, поэтому

Z_экв = Z₁ + Z₂₃ = 8 + j6 + 6,67 + j3,33 = 14,67 + j9,33 Ом.

Определяем ток по закону Ома

/Z_экв = 



Действующее значение тока



Зная ток , можно рассчитать напряжение , для чего:

рассчитывается падение напряжения на участке с сопротивлением Z₁:

Z₁ = (1,94-j1,23)(8 + j6) = 15,52-j9,84 + j11,64 + 7,38 = 22,9 + j1,8 B,

затем в соответствии со вторым законам Кирхгофа



Напряжение можно определить по закону Ома

·Z₂₃ = (1,94 - j1,23)(6,67 + j3,33) = 12,94-j8,2 + j6,46 + 4,1 = 

  = 17,04-j1,74 B.

Определяем токи и

/Z₂ = 

1,77 – j2,94 А;



/Z₃ = 





Проверка:

1,94 - j1,23 - 1,77 + j2,94 - 0,17 - j1,7 = 0 + j0,01 ≈ 0.

Строим векторную диаграмму, откладывая в масштабе на комплексной плоскости векторы токов и напряжений (рис. 2.10).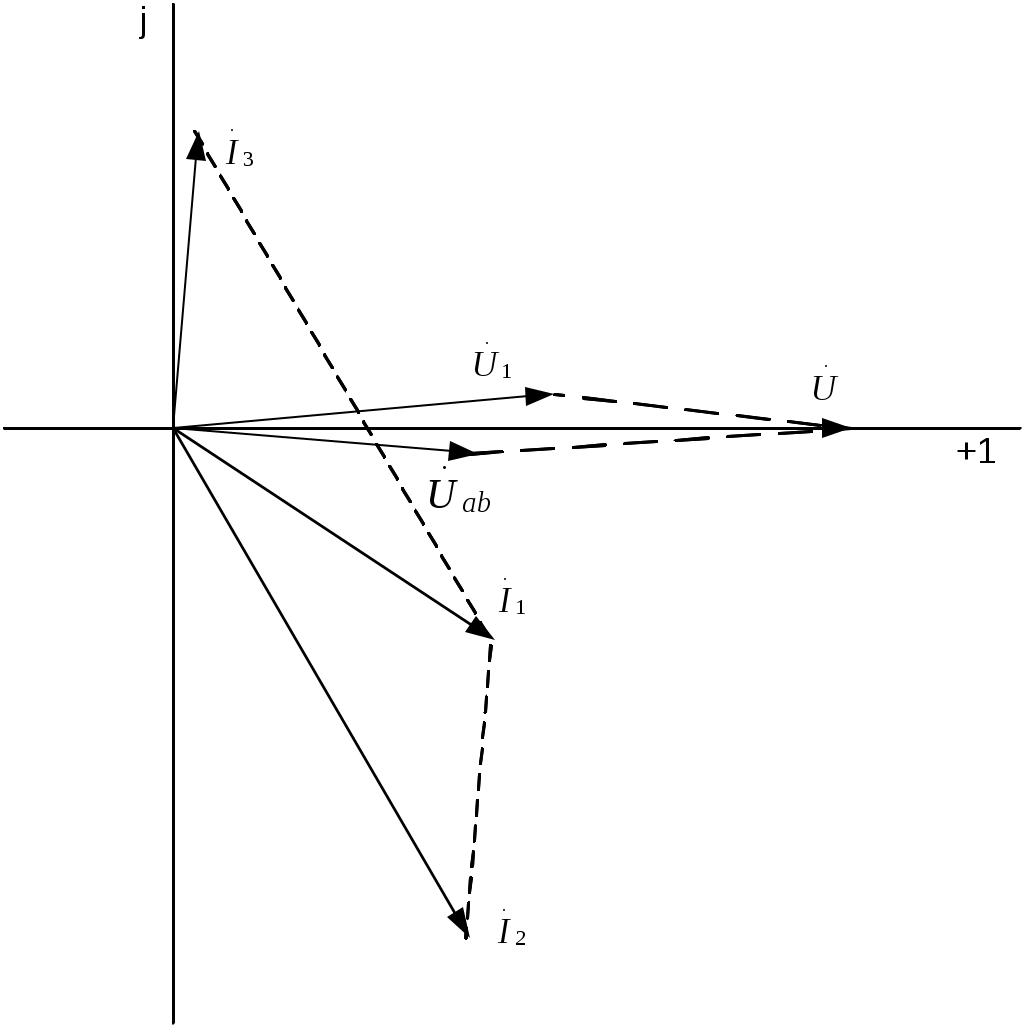



Рис. 2.10

2.3.8. Определить показания вольтметра PV1 (рис. 2.11), если амперметр PA1 показывает ток I₃ = 10 A.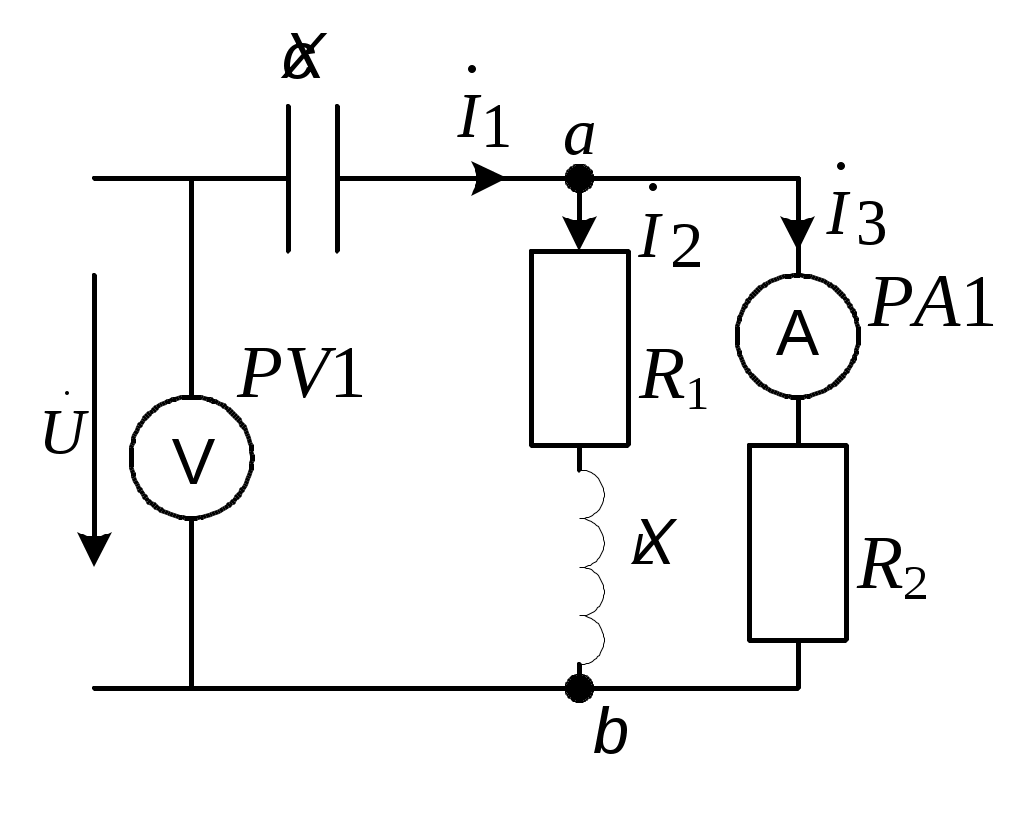



X_C = 5 Ом;

R₁ = 6 Ом;

X_L = 8 Ом;

R₂ = 10 Ом.

Рис. 2.11

Решение

Принимаем начальную фазу тока ψ_i3 = 0, тогда

Комплексные сопротивления ветвей:

Z₁ = -jX_C = -j5 Ом;

Z₂ = R₁ + jX_L = 6 + j8 Ом;

Z₃ = R₂ = 10 Ом.

Напряжение на участке с параллельным соединением ветвей

·Z₃ = 10·10 = 100 В.

По закону Ома ток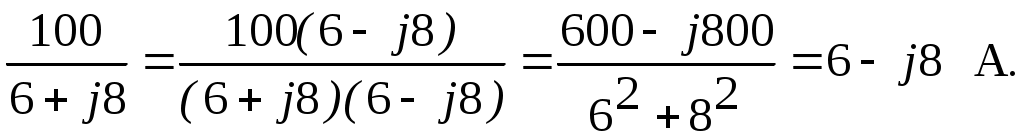

/Z₂ = 

По первому закону Кирхгофа ток на неразветвленном участке



Тогда напряжения

·Z₁ = (16 - j8)(-j5) = -40 - j80 В;



Действующее значение напряжения



2.4. Задачи для самостоятельного решения

2.4.1. Ток в ветви изменяется гармонически с амплитудой 2 А и частотой 50 Гц. Написать выражение для мгновенного значения тока в виде синусоидальной функции времени, приняв за начала отсчета времени точки 0₁, 0₂, 0₃ и 0₄ (рис. 2.12) .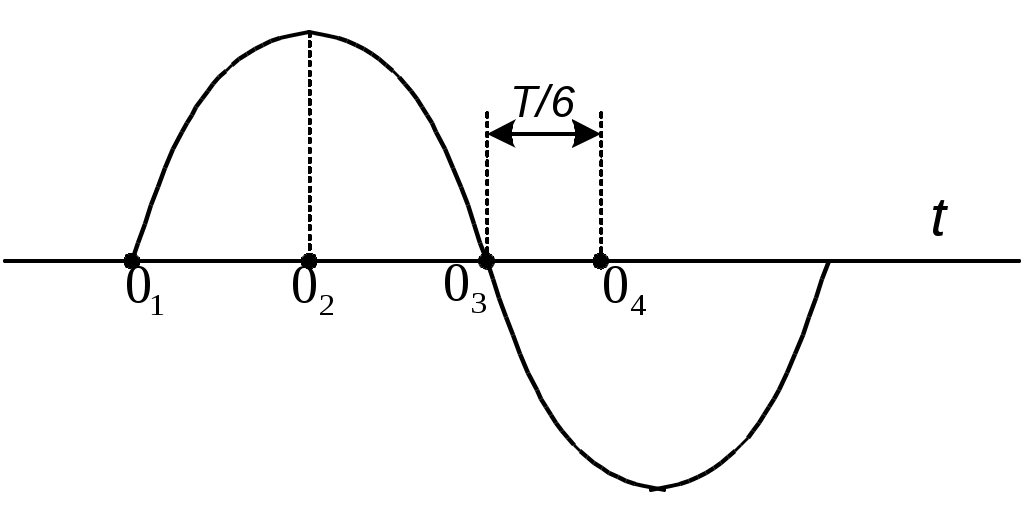



Рис.2.12

2.4.2. Выражение мгновенного значения синусоидального тока имеет вид: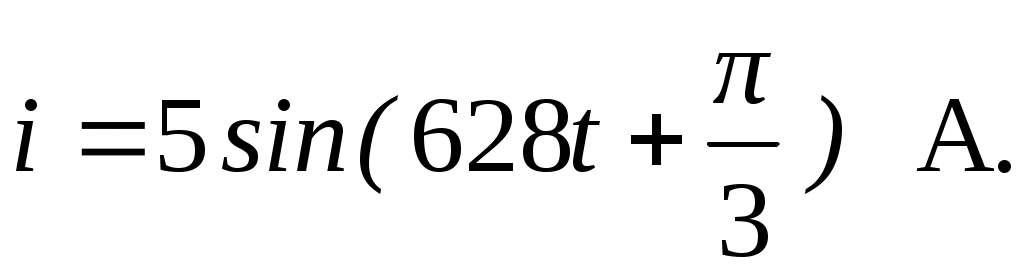

Определить период Т, частоту f, действующее значение тока I. Нарисовать синусоиду тока и построить на комплексной плоскости вектор изображающий данный ток.

2.4.3. Определить ток i (рис. 2.13), если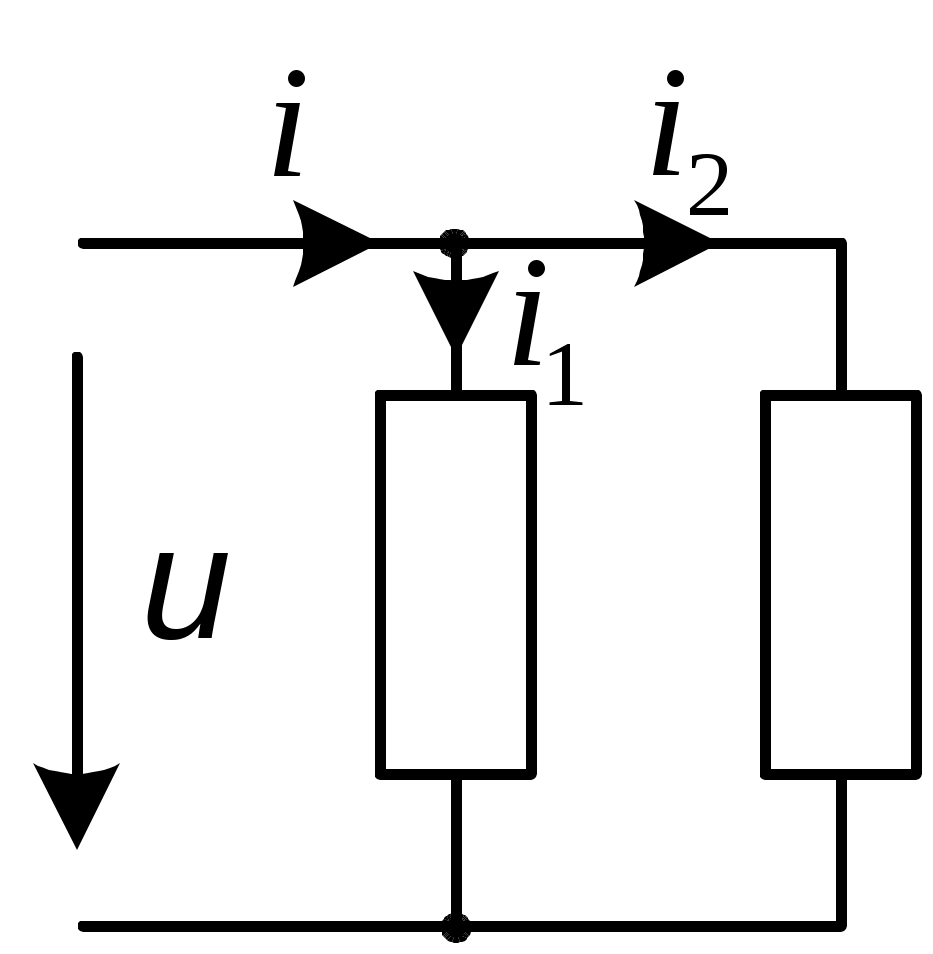



Рис. 2.13

2.4.4. Записать выражение мгновенного значения синусоидального напряжения, если комплексное действующее значение напряжения



2.4.5. Определить показание амперметра (рис. 2.14).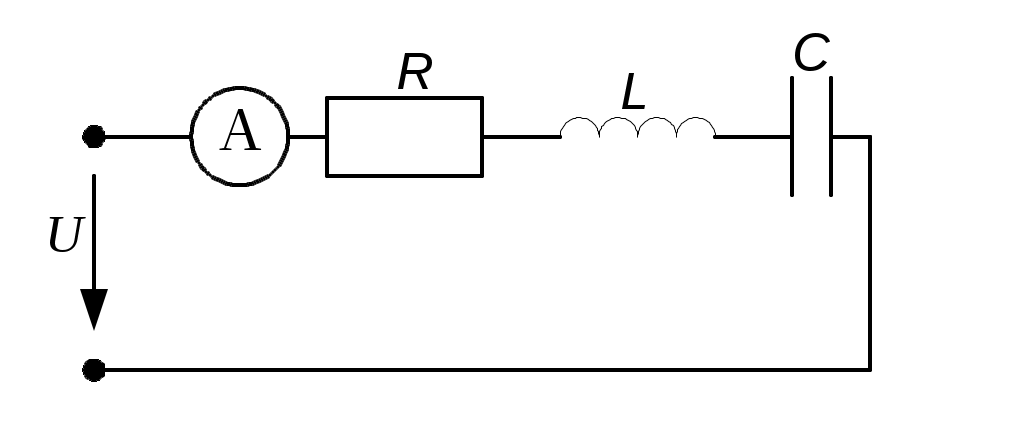

Построить векторную диаграмму

тока и напряжений.

u = 311,1sin314t B; R = 60 Ом;

Рис. 2.14 L = 318 мГн; C = 159 мкФ.

Задачу решить комплексным методом. Ответ: I = 2,2 A.

2.4.6. В цепи состоящей из последовательно соединенных конденсатора (C = 50 мкФ) и катушки (L = 10 мГн, R = 10 Ом), ток i = 0,2sin1000t A.

Найти мгновенные значения напряжения на конденсаторе, катушке и всей цепи. Задачу решить комплексным методом.

Ответ: u_C = 4sin(1000t-90º) B; u_K = 2,83sin(1000t + 45º)B; u = 2,83sin(1000t-45º) B.

2.4.7. В схеме (рис. 2.15), протекающий ток отстает от приложенного к цепи напряжения на 45º; R = 50 Ом; C = 3,18 мкФ; f = 500 Гц. Определить индуктивность L, приложенное напряжение 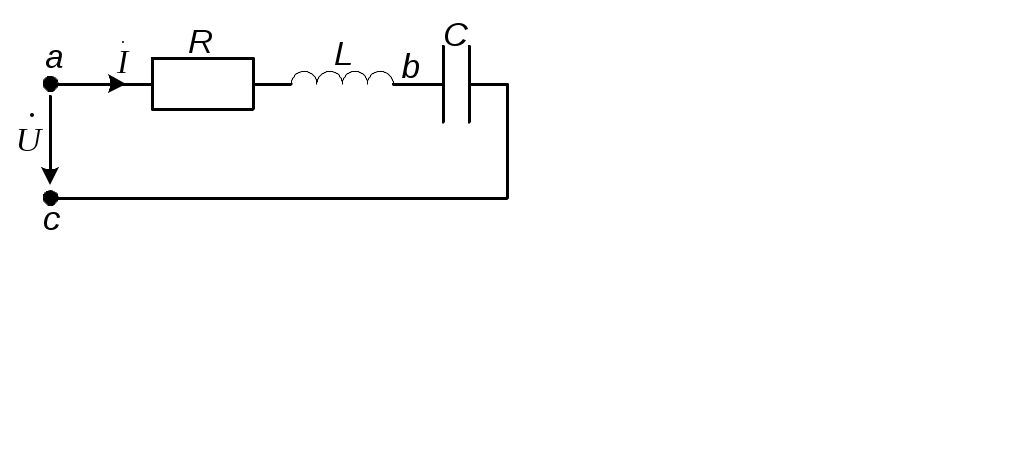и ток в цепи , если Записать выражение для комплексного сопротивления цепи.



Рис. 2.15

Ответ: L = 47,6 мГн; Z = 

2.4.8. В схеме (рис. 2.16), при разомкнутом выключателе сдвиг фаз между напряжением 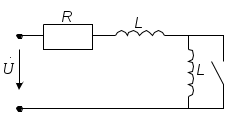и током , φ₁ = 60°. Найти сдвиг фаз между ними при замкнутом выключателе. Ответ: φ₂ = 41°.



Рис. 2.16

2 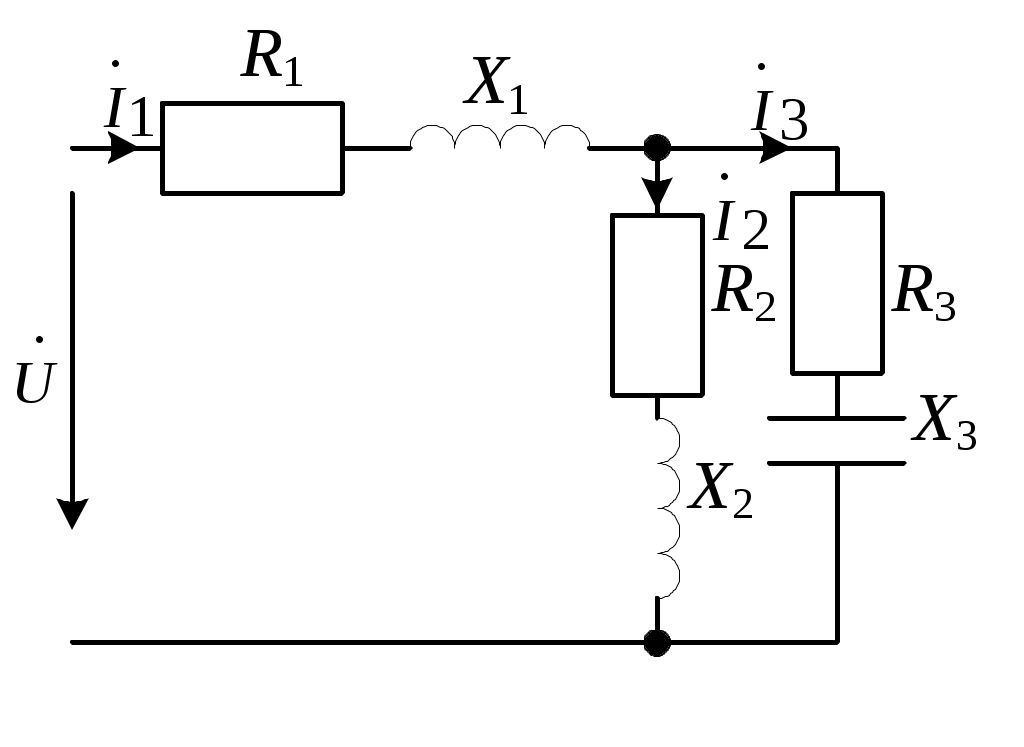.4.9. Определить комплексные токи в цепи (рис. 2.17) и построить векторную диаграмму токов и напряжений. U = 100 В; R₁ = 6 Ом; X₁ = = 8 Ом; R₂ = 3 Ом; X₂ = 7 Ом; R₃ = 2 Ом; X₃ = 2 Ом.