Электрических цепей постоянного тока
 Скачать 5.4 Mb. Скачать 5.4 Mb.
|
Рис. 2.17Ответ: 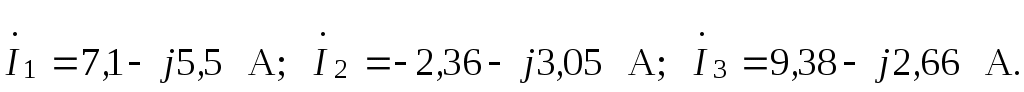 2.4.10. В цепи, схема которой представлена на (рис. 2.18), R = 10 Ом; L = 5,97 мГн; C = 33,2 мкФ. На входе цепи приложено напряжение U = 100 B, частота 400 Гц. Считая начальную фазу напряжения на входе равной нулю, определить комплексные токи ветвей. Р | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Номер варианта | Выражение тока i |
| 1 | i = 400sin(314t + 135°) |
| 2 | i = 5sin(314t – p/6) |
| 3 | i = 80sin(942t + 60°) |
| 4 | i = 15sin(628t + p/2) |
| 5 | i = 205sin(628t – 120°) |
| 6 | i = 40sin(157t – 240°) |
| 7 | i = 60sin(314t + p/3) |
| 8 | i = 25sin(314t – 60°) |
| 9 | i = 30sin(314t + p/6) |
| 10 | i = 70sin(157t – p/4) |
| 11 | i = 20sin(157t – p/2) |
(продолжение табл.2.1)
| 12 | i = 127sin(1256t + 60°) |
| 13 | i = 127sin(157t – 2p/3) |
| 14 | i = 200sin(314t – p/2) |
| 15 | i = 220sin(780t + 2p/3) |
2.5.2. Для заданной цепи согласно варианту (табл. 2.2) определить величины, указанные в таблице, и построить векторную диаграмму тока и напряжений. Расчет выполнить комплексным методом.
Таблица 2.2
| № вар. | Дано | Рис. № | Определить |
| 1 | U = 100 B; R = 8 Ом; XL = 10 Ом; XC = 4 Ом | 2.20 | I; UR; UL; UC |
| 2 | I = 8 А; XL1 = 2 Ом; XL2 = 4 Ом; R = 8 Ом | 2.21 | U; UR; UL1; UL2 |
| 3 | U = 100 B; R1 = 2 Ом; R2 = 4 Ом; XL = 8 Ом | 2.22 | I; UR1; UR2; UL |
| 4 | UR = 100 B; R = 20 Ом; XC = 15 Ом | 2.23 | I; U; UC |
| 5 | U = 40 B; R1 = 11 Ом; R2 = 5 Ом; XС = 12 Ом | 2.24 | I; UR1; UR2; UC |
| 6 | I = 2 А; R = 8 Ом; XL = 12 Ом; XC = 6 Ом | 2.20 | U; UR; UL; UC |
(продолжение табл.2.2)
| 7 | I = 2 А; R = 12 Ом; XС1 = 10 Ом; XC2 = 6 Ом | 2.26 | U; UR; UC1; UC2 | |
| 8 | U = 60 B; R = 3 Ом; XL1 = 1 Ом; XL2 = 3 Ом | 2.21 | I; UR; UL1; UL2 | |
| 9 | I = 5 А; R1 = 7 Ом; R2 = 5 Ом; XL = 16 Ом | 2.22 | U; UR1; UR2; UL | |
| 10 | UС = 40 B; R = 6 Ом; XC = 8 Ом | 2.23 | I; U; UR | |
| 11 | I = 10 А; R1 = 5 Ом; R2 = 3 Ом; XС = 6 Ом | 2.24 | U; UR1; UR2; UC | |
| 12 | U = 50 B; R = 8 Ом; XC1 = 2 Ом; XC2 = 4 Ом | 2.25 | I; UR; UC1; UC2 | |
| 13 | U = 80 B; R = 8 Ом; XL1 = 2 Ом; XL2 = 4 Ом | 2.21 | I; U; UL1; UL2 | |
| 14 | UR = 20 B; R = 4 Ом; XL = 7 Ом; XC = 4 Ом | 2.20 | I; U; UL; UC | |
| 15 | UC2 = 60 B; R = 12Ом; XС1 = 10 Ом;XC2 = 6Ом | 2.25 | I; U; UR; UC | |

Рис. 2.20 Рис. 2.21 Рис. 2.22

Рис. 2.23 Рис. 2.24 Рис. 2.25
2.5.3 К источнику с синусоидальным напряжением U подключена цепь со смешанным соединением сопротивлений Z1, Z2, Z3 (табл. 2.3). Нарисовать схему цепи, обозначить токи и напряжения в ней. Определить ток в неразветвлённой части цепи.
Таблица 2.3
| № варианта | U, В | Z1, Ом | Z2, Ом | Z3, Ом |
| 1 | 50 | 2,8 + j2,1 | 1 + j2 | 3 |
| 2 | 400 | 8 – j29 | 10 + j20 | 30 |
| 3 | 10 | 0,4 – j0,8 | 1 | 1 – j |
| 4 | 80 | 0,9 + j0,3 | j | 1 + j2 |
| 5 | 100 | 2,6 + j2,8 | 2 + j2 | j2 |
| 6 | 200 | 0,2 + j0,6 | 1 + j | 2 |
| 7 | 20 | 0,8 + j0,4 | 1 + j | j |
| 8 | 200 | 9 + j3 | j10 | 10 + j20 |
| 9 | 100 | 1 – j3 | – j5 | 4 + j2 |
| 10 | 500 | 10 – j30 | 40 + j20 | – j50 |
| 11 | 100 | 2,6 – j2,8 | 2 – j2 | – j2 |
| 12 | 50 | 1 – j3 | 4 + j2 | – j5 |
| 13 | 80 | 0,9 + j0,3 | j | 1 + j2 |
| 14 | 200 | 10 – j30 | – j30 | 40 + j20 |
| 15 | 500 | 26 – j28 | 20 – j20 | – j20 |
2.6. Контрольные вопросы
Что такое период, частота?
Как определяется угловая частота?
Что такое фаза, начальная фаза?
Что называют началом синусоиды?
Как определяется действующее значение синусоидального тока?
Каковы правила изображения синусоидальной функции вектором?
Что значит комплексная амплитуда, как её записать?
Что значит комплексное действующее значение, как его получить?
Как осуществить переход от комплексной амплитуды и комплексного действующего значения к выражению мгновенного выражения величины?
10. Чему равно индуктивное сопротивление?
11. Чему равно ёмкостное сопротивление?
12. Что значит реактивное сопротивление?
13. Что такое комплексное сопротивление?
14. Что значит полное сопротивление?
15. Что такое треугольник сопротивлений?
16. Что такое угол φ и как он определяется?
17. Запишите закон Ома в комплексной форме.
18.Что можно сказать о сдвиге по фазе между напряжением и током на R, L и C?
19. Как строятся векторные диаграммы тока и напряжений?
20. Каков порядок расчета цепи переменного тока со смешанным соединением элементов?
21. Почему расчет цепи переменного тока ведут в комплексной форме?
Тема 3
МЕТОДЫ РАСЧЕТА СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
3.1 Расчет сложных электрических цепей, основанный на применении уравнений Кирхгофа и по методу контурных токов
Цель: Научиться составлять уравнения по законам Кирхгофа в дифференциальной и комплексной формах. Приобрести практические навыки по расчету сложных цепей методом уравнений Кирхгофа. Освоить метод контурных токов.
3.1 Задание по самоподготовке
Повторить вопросы из тем 1 и 2, касающиеся определения понятий ветвь, узел, контур, формулировки первого и второго законов Кирхгофа и правила составления уравнений по ним (для электрических цепей постоянного тока, для мгновенных значений, комплексов действующих значений токов, падений напряжений, ЭДС в цепях синусоидального тока).
Проработать тему “Составление уравнений по законам Кирхгофа” по учебнику [I] §1.7, 1.8, 3.16. и по конспекту лекций.
Разобрать пример 2, §1.8 [1] и примеры 3.3.1 и 3.3.2 данных методических указаний.
4. Проработать тему “Метод контурных токов” по литературе [1] §1.13 и по конспекту лекций.
5. Разобрать пример 5, §1.13 [1] и пример 3.3.3 данных методических указаний.
Ответить на контрольные вопросы п. 3.6.
3.2 Общие сведения
С помощью уравнений Кирхгофа проводят расчет сложных цепей постоянного и синусоидального токов.
Первый закон Кирхгофа. Алгебраическая сумма мгновенных токов в узле равна 0.
Второй закон Кирхгофа. Алгебраическая сумма мгновенных ЭДС в замкнутом контуре равна алгебраической сумме мгновенных напряжений на остальных элементах этого контура
Для цепей синусоидального тока законы Кирхгофа записываются в комплексной форме.
Первый закон Кирхгофа. Алгебраическая сумма комплексных токов в узле равна нулю
Второй закон Кирхгофа. Алгебраическая сумма комплексных ЭДС замкнутого контура равна алгебраической сумме комплексных напряжений на остальных элементах этого контура.
Порядок составления системы уравнений по законам Кирхгофа:
Произвольно задают положительные направления токов в ветвях и обозначают их на схеме. Эти направления нельзя менять до окончания расчета.
Произвольно задают положительные направления обходов по контурам и наносят их на схеме.
Рекомендуется положительные направления обходов по всем контурам принимать одинаково.
Составляют уравнения по первому закону Кирхгофа. Число уравнений должно быть на единицу меньше, чем число узлов.
Составляют уравнения по второму закону Кирхгофа. Число этих уравнений, совместно с уже составленными уравнениями по первому закону Кирхгофа, должно равняться числу ветвей. Чтобы уравнения были независимыми, каждый контур, для которого составляется уравнение по второму закону Кирхгофа, должен отличаться от предыдущих хотя бы одной новой ветвью. Это условие является достаточным, но не всегда необходимым.
Решают систему уравнений, в результате чего находят токи в ветвях.
Если ток получен со знаком “минус”, это означает, что ток имеет положительное направление противоположное ранее принятому.
Примечания: 1. При составлении независимых уравнений по второму закону Кирхгофа не включают ветви, содержащие источники тока (см. пример 3.3.1).
2. При составлении уравнений по закону Кирхгофа в дифференциальной форме необходимо знать соотношения между мгновенными значениями токов и напряжений на участках R, L, C.
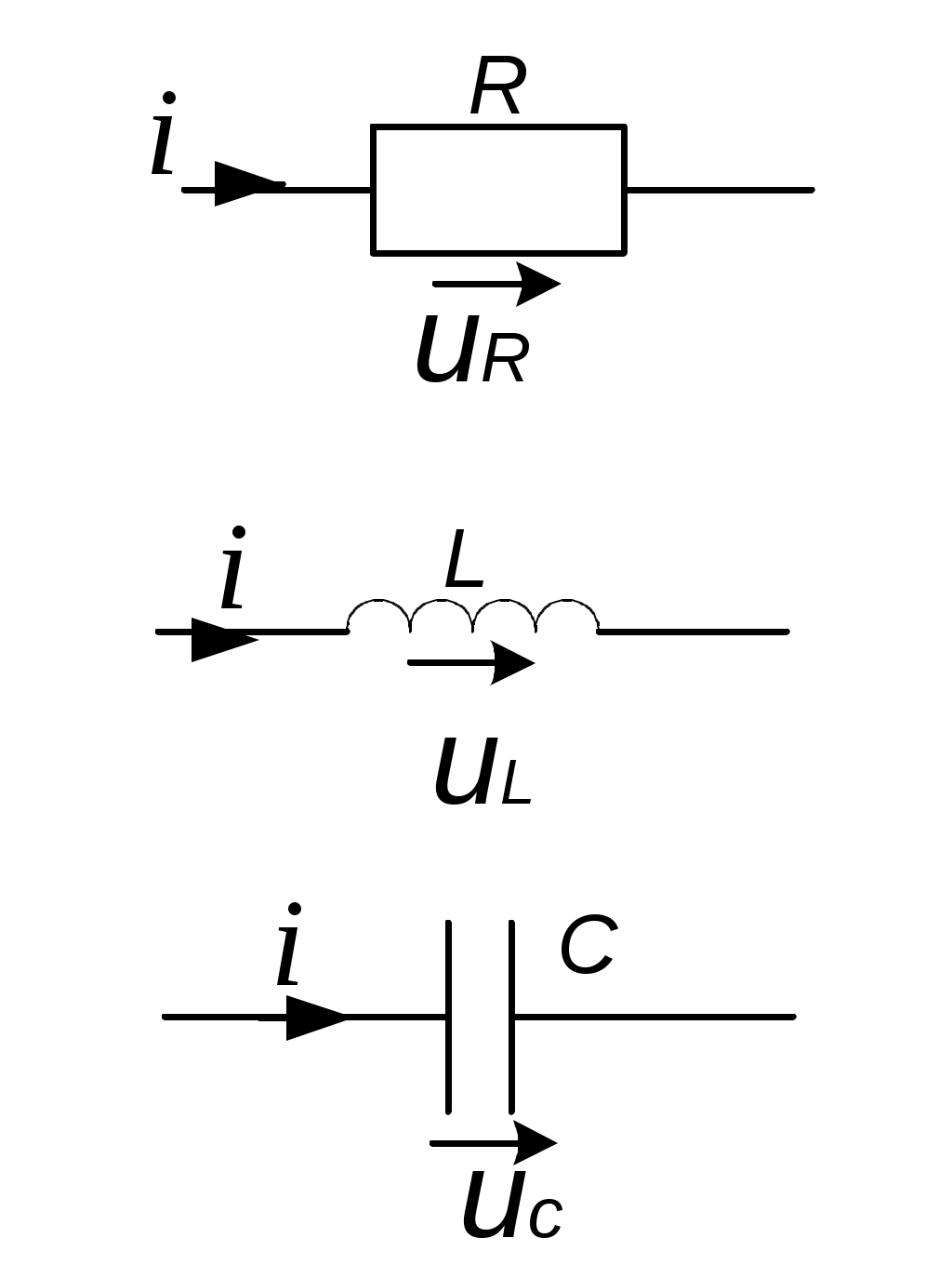 а)
а) б)
в)
Метод контурных токов основан на предположении, что в каждом независимом контуре протекает свой контурный ток. Следует особо подчеркнуть, что контурный ток – это искусственный ток, вводимый для упрощения расчета сложных электрических цепей. Для определения контурных токов составляются уравнения по второму закону Кирхгофа.
Порядок определения токов методом контурных токов
Произвольно задают положительные направления токов в ветвях и обозначают их на схеме.
Произвольно задают положительные направления контурных токов и обозначают их на схеме. Направление контурных токов соответствует направлению обхода по контуру.
Составляют систему уравнений по второму закону Кирхгофа для контуров.
Решая систему, определяют контурные токи.
По значениям контурных токов определяют действительные токи в ветвях. Токи в ветвях определяются алгебраической суммой соответствующих контурных токов, проходящих по данной ветви.
Положительными считаются те контурные токи, направление которых совпадают с выбранным в начале расчета положительным направлением тока данной ветви.
Примечание: Если электрическая цепь содержит источник тока, подсоединенный к каким – либо узлам («m», «n»), то считают, что ток источника тока есть контурный ток, проходящий по ветвям, соединяющим эти узлы «m» и «n».
В уравнениях, составленных по второму закону Кирхгофа для контуров, включающих эти ветви, должно быть учтено падение напряжения от тока источника тока (см. пример 3.3.3).
3.3 Примеры
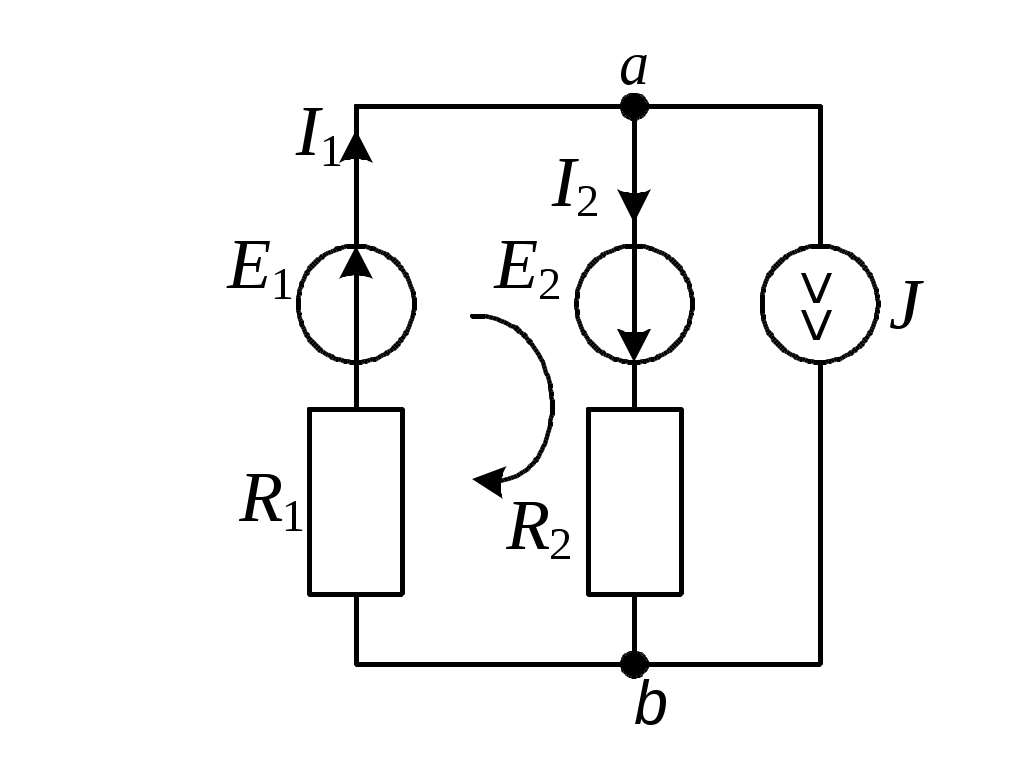
3.3.1. Определить токи в ветвях электрической цепи постоянного тока (рис 3.1), используя уравнения Кирхгофа. Дано:
 E1 = 10 B;
E1 = 10 B;R1 = 1 Ом;
R2 = 2 Ом;
Рис. 3.1 E2 = 2 В;
J = 3 A.
Решение
Цепь содержит две ветви с неизвестными токами.
Для определения этих токов составляем одно уравнение по первому закону Кирхгофа и одно уравнение по второму закону Кирхгофа.
Задаемся положительным направлением токов в ветвях и обозначаем их на схеме.
Задаемся положительным направлением обхода по контуру и наносим на схеме.
Составляем уравнение по первому закону Кирхгофа для узла а
Составляем уравнение по второму закону Кирхгофа
Решаем систему уравнений
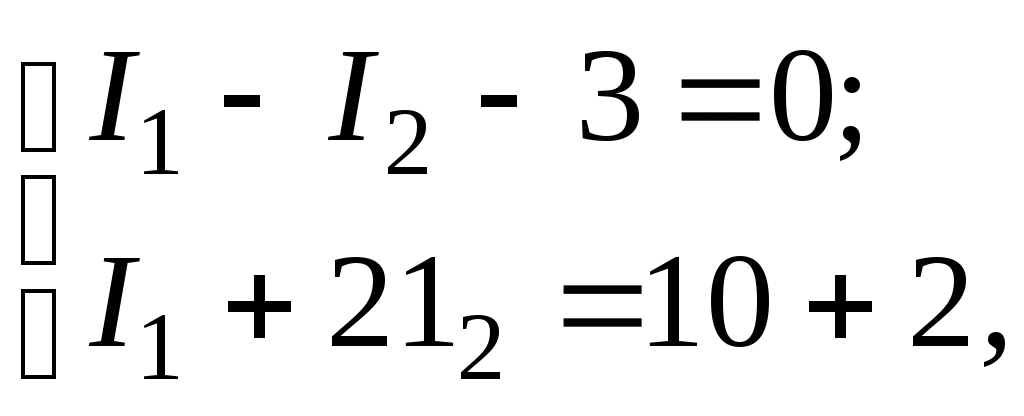
применяя метод исключения переменных
I1 = I2 + 3; I2 + 3 + 2I2 = 12; 3I2 = 9; I2 = 3 A;
I1 = 3 + 3 = 6 A.
3.3.2. Определить токи в ветвях электрической цепи синусоидального тока (рис. 3.2), используя законы Кирхгофа, если
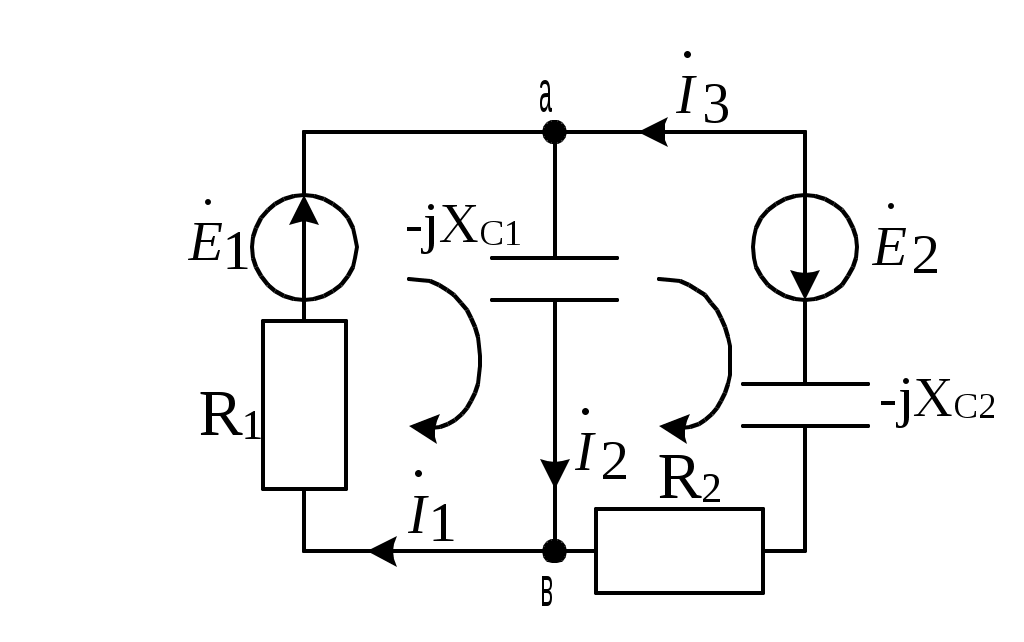
Рис. 3.2
Решение
Задаемся положительными направлениями токов в ветвях и обозначаем их на схеме.
Задаемся направлением обхода по контурам.
Составляем систему уравнений, используя два закона Кирхгофа, в комплексной форме
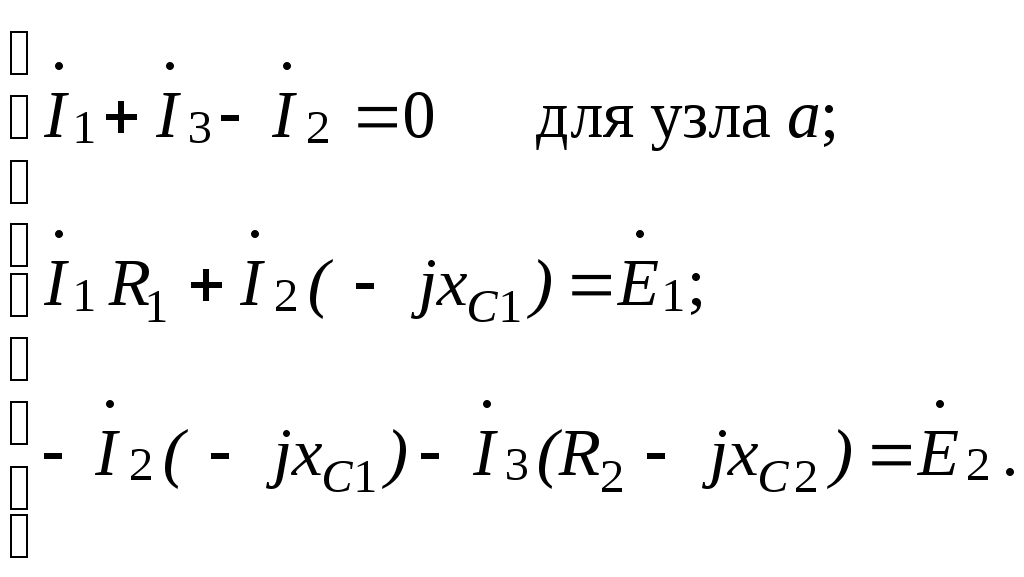 (3.1)
(3.1)Подставив в систему уравнений (3.1) известные величины, имеем:
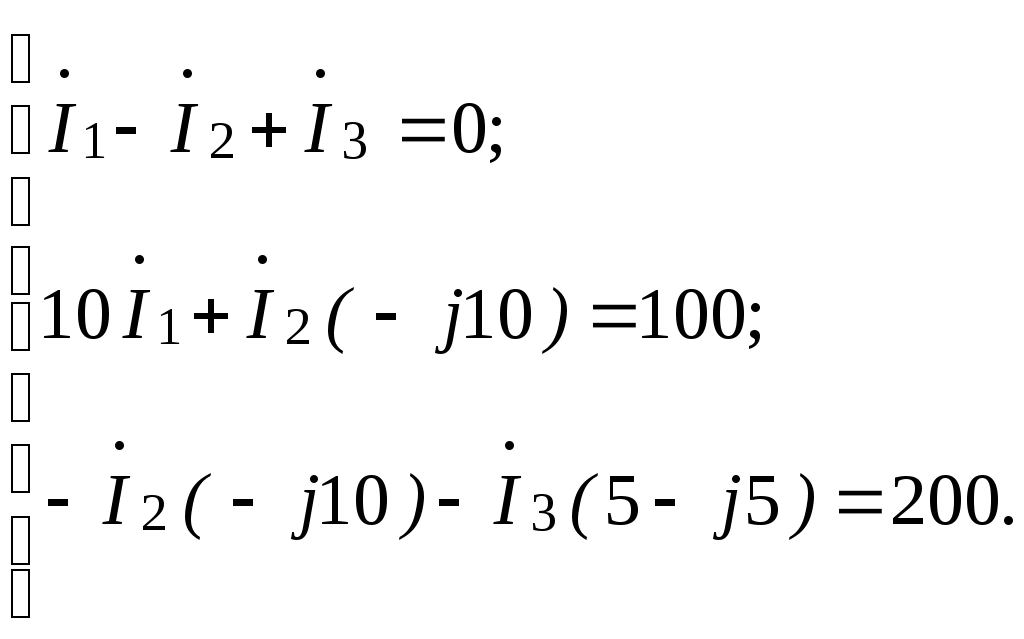 (3.2)
(3.2)после упрощения системы уравнений (3.2) имеем:
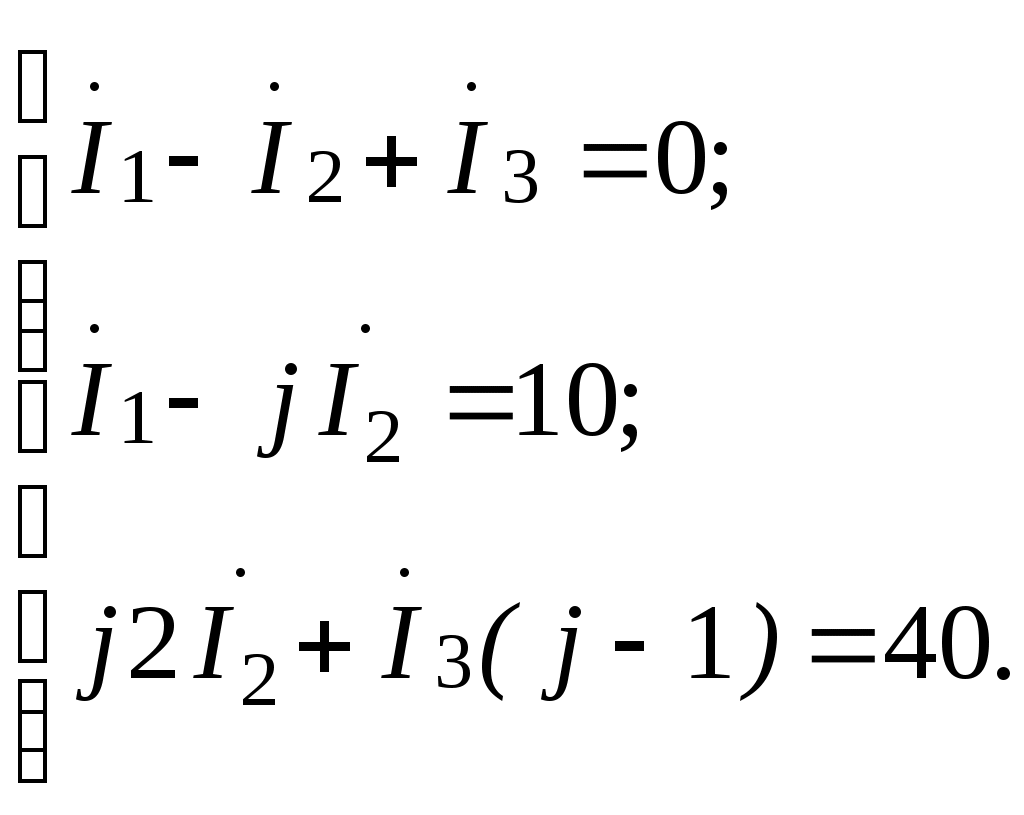 (3.3)
(3.3)Решаем систему уравнений (3.3) методом определителей:
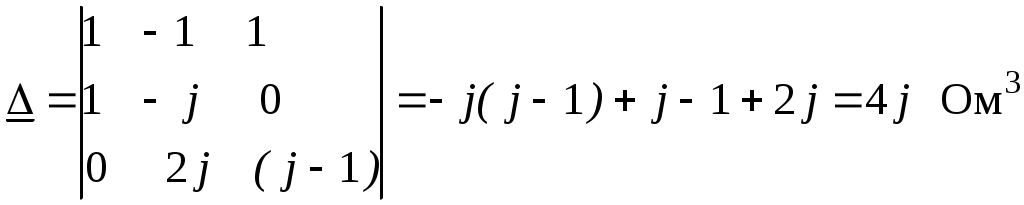
Раскрытие определителя – см. Приложение 1.
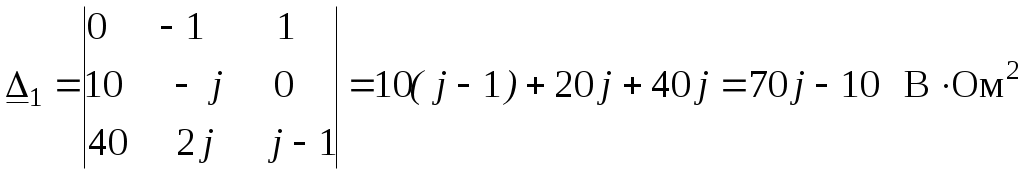 .
.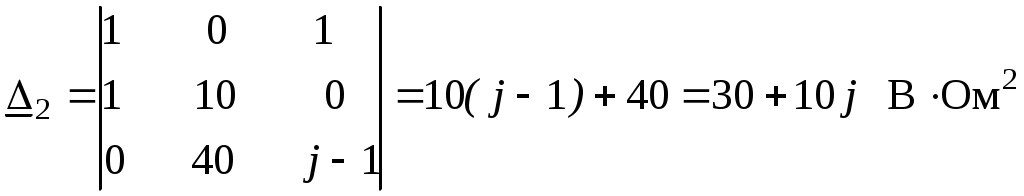 .
.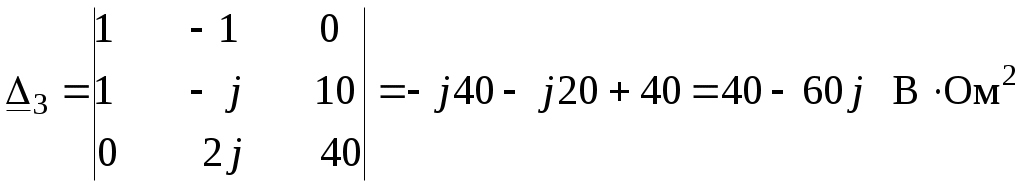 .
.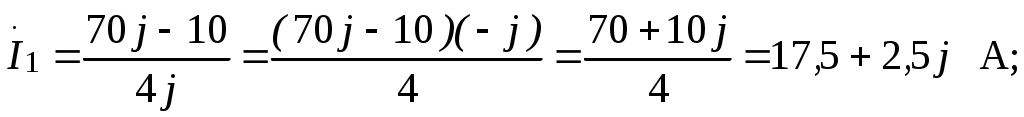
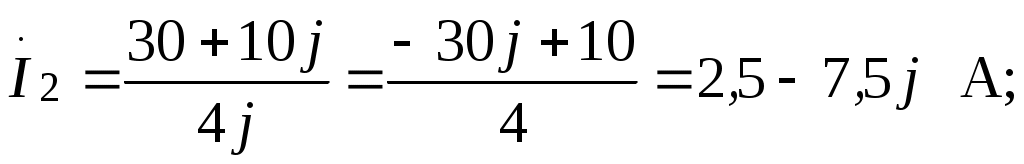
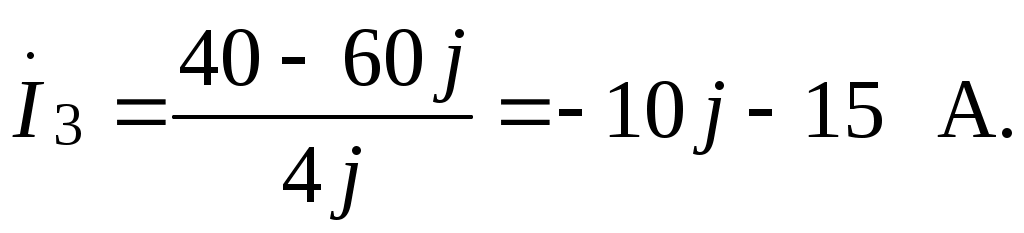
Действующие значения токов
Систему уравнений (3.3) можно решить методом исключения переменных, а именно из второго уравнения системы (3.3)
Выражение
откуда следует, что
Выражение тока
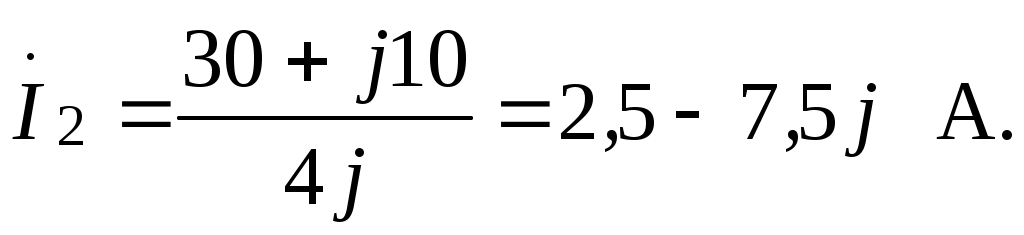
Следовательно,
3
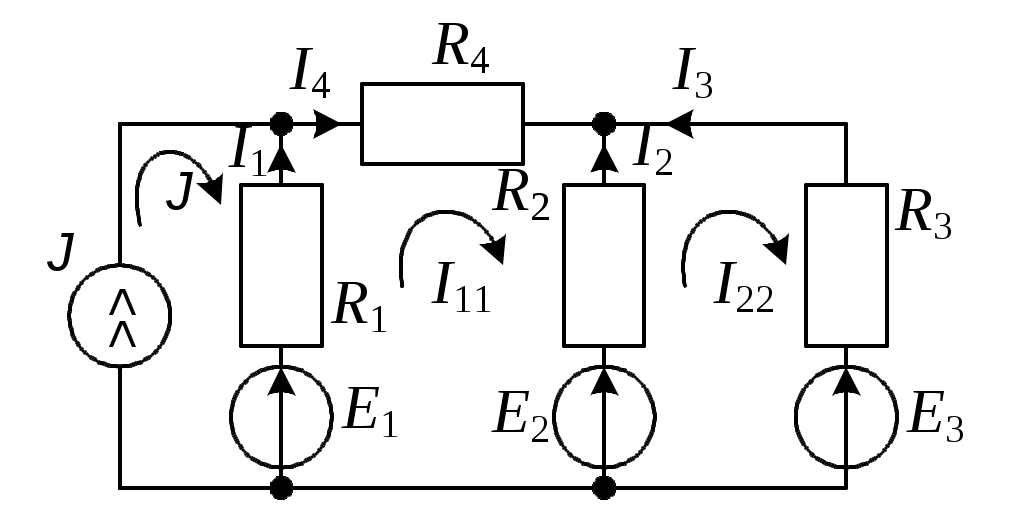 .3.3. Определить токи в ветвях электрической цепи (рис. 3.3) по методу контурных токов, если
.3.3. Определить токи в ветвях электрической цепи (рис. 3.3) по методу контурных токов, еслиE1 = 20 B; E3 = 50 B;
E2 = 40 B; J = 4 A;
R1 = 10 Ом; R2 = 3 Ом;
R3 = 2 Ом; R4 = 7 Ом.
Рис. 3.3
Решение
Задаемся положительным направлением токов в ветвях и обозначаем их на схеме.
Задаемся положительным направлением контурных токов
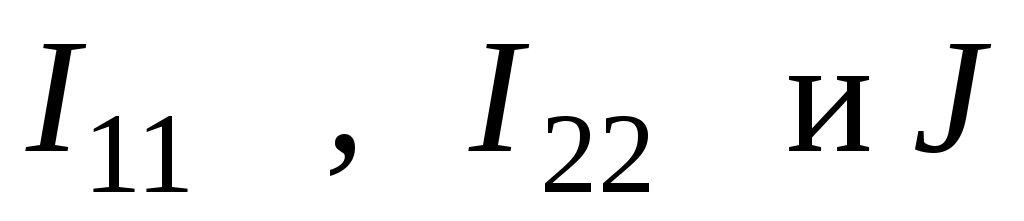 .
.Составляем систему уравнений
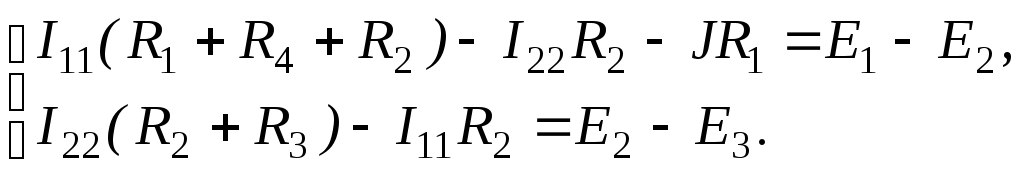
4. Подставляем в составленную систему уравнений известные величины и, решая ее, определяем контурные токи
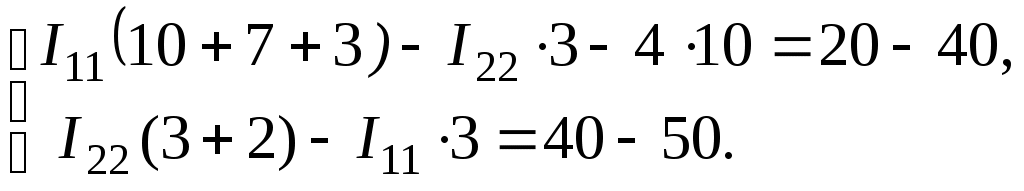
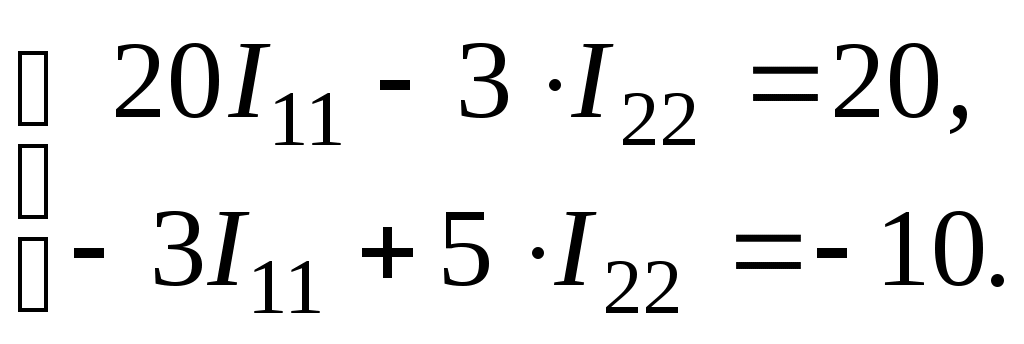
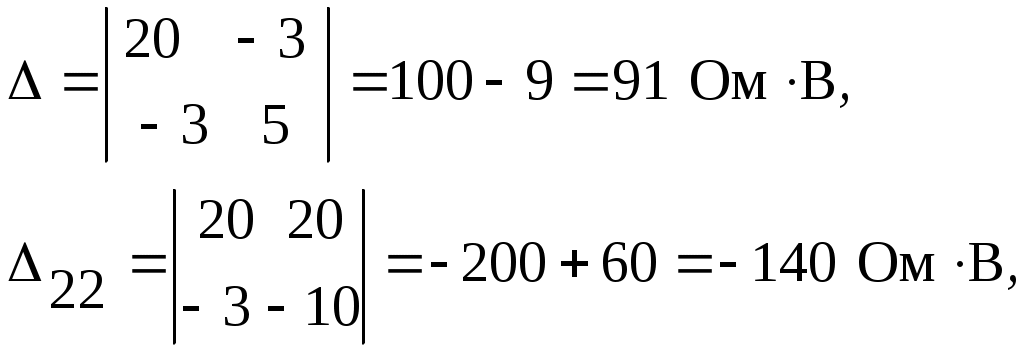
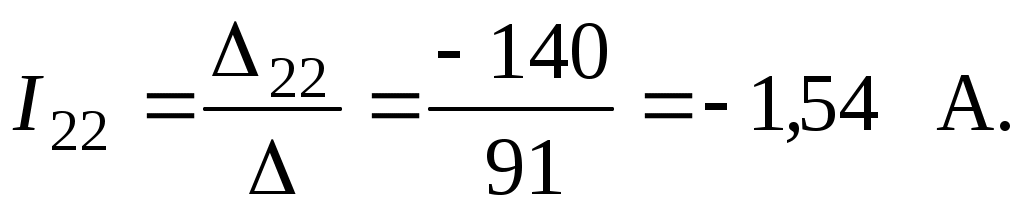
5. Определяем токи в ветвях
3.4 Задачи для самостоятельного решения
3.4.1. Составить систему уравнений по законам Кирхгофа для электрической цепи постоянного тока (рис. 3.4)
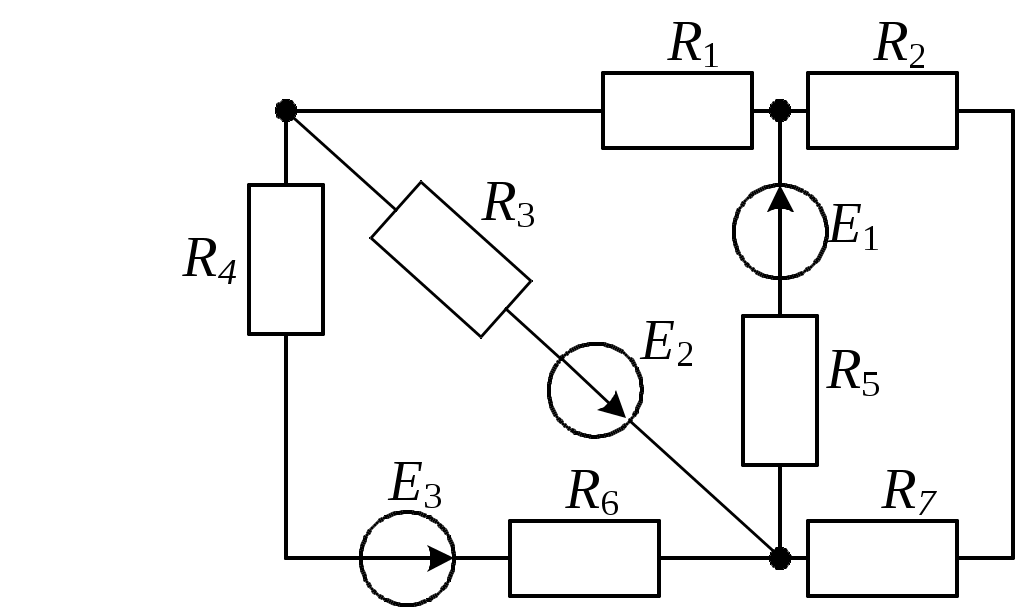
Рис. 3.4
3
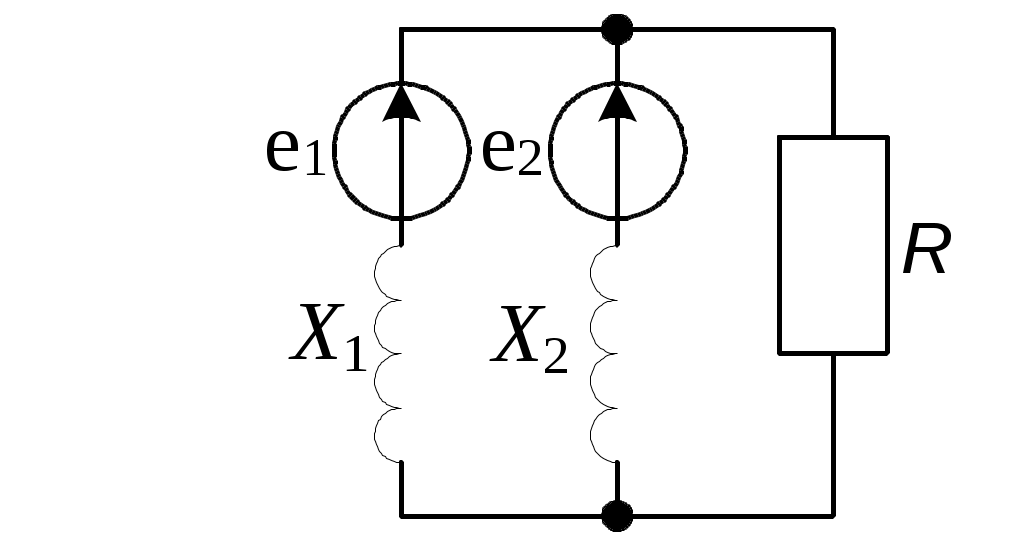 .4.2. Определить токи в ветвях электрической цепи (рис. 3.5), используя первый и второй законы Кирхгофа, если e1 = e2 = 141sinωt B; X1 = = 5 Ом; X2 = 20 Ом; R = 3 Ом. Ответ:
.4.2. Определить токи в ветвях электрической цепи (рис. 3.5), используя первый и второй законы Кирхгофа, если e1 = e2 = 141sinωt B; X1 = = 5 Ом; X2 = 20 Ом; R = 3 Ом. Ответ:Рис. 3.5
3.4.3. Определить токи в ветвях электрической цепи (рис. 3.6) методом контурных токов, если: E1 = 11 В, R1 = 10 Ом, R2 = 2 Ом, E2 = 2 B, J= 3 A. Ответ: I1 = 1,25 A, I2 = 1,75 A.
3.4.4. Определить токи в ветвях электрической цепи (рис. 3.7) методом контурных токов, если е1 = 141sinωt B, е2 = 141 sinωt B, Х1 = 5 Ом, Х2 = 20 Ом, R = 3 Ом. Ответ: I1 = 16 A, I2 = 4 A, I2 = 20 А.
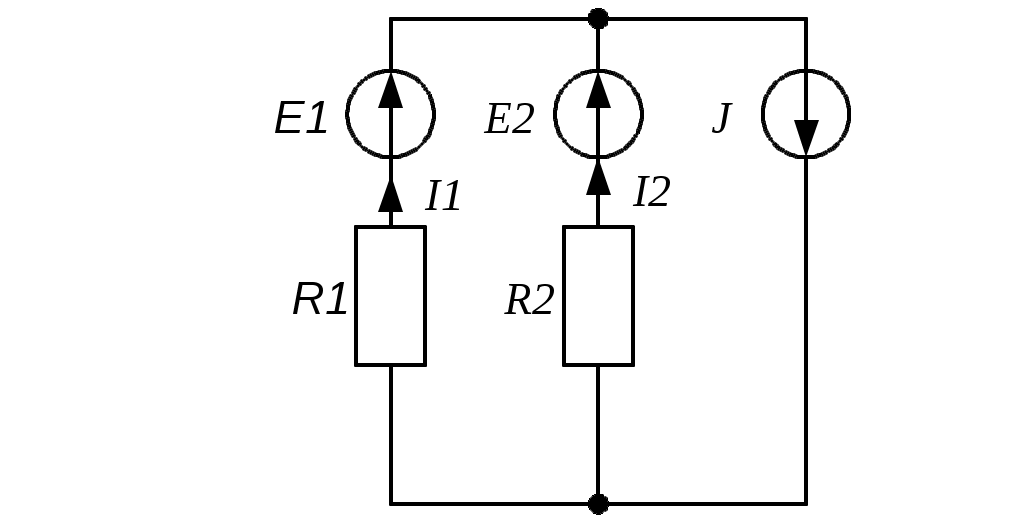
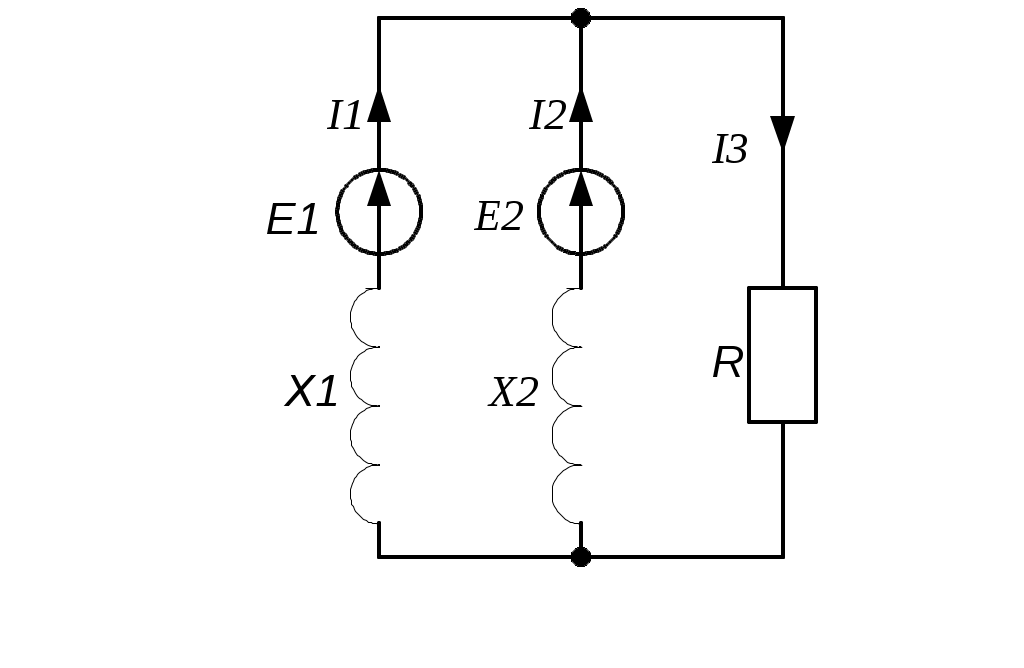
Рис. 3.6 Рис. 3.7
3.5 Индивидуальные задания
В электрических цепях постоянного тока (рис. 3.8 – 3.12) заданы ЭДС и сопротивления (табл. 3.1).
Вычертить схему электрической цепи согласно заданному варианту.
Определить токи в ветвях, используя первый и второй законы Кирхгофа.
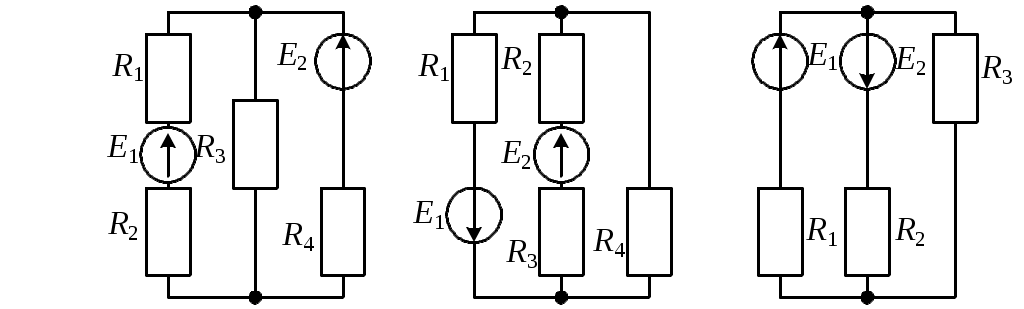
Рис. 3.8 Рис. 3.9 Рис. 3.10
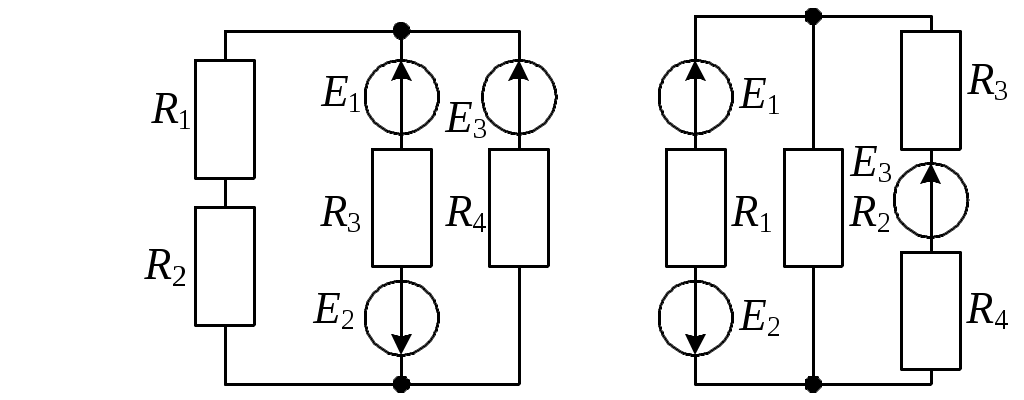
Рис. 3.11 Рис. 3.12
Таблица 3.1
-
Номер вар.
Cхема цепи
Элементы, входящие в электрическую цепь, Ом
E1, B
E2, B
E3, B
R1,Ом
R2,Ом
R3,Ом
R4,Ом
1
3.8
20
40
–
4
6
10
5
2
3.9
60
20
–
10
3
0
4
3
3.10
100
20
60
10
20
10
–
4
3.11
120
20
50
4
6
20
10
5
3.12
40
20
10
5
2
0
5
6
3.8
100
50
–
0
10
20
40
7
3.9
80
30
–
2
3
7
10
8
3.10
0
40
60
5
10
4
–
9
3.11
50
30
20
0
10
5
20
10
3.12
0
20
50
10
2
3
7
11
3.8
100
20
–
8
0
5
10
12
3.9
40
80
–
10
0
20
5
13
3.10
0
0
200
20
10
3
–
14
3.11
100
100
50
10
20
6
4
15
3.12
80
0
40
10
20
10
0
3.5.2. В электрических цепях постоянного тока (рис. 3.13 – 3.17) заданы ЭДС и сопротивления (табл. 3.2). Необходимо:
1. Вычертить схему электрической цепи согласно заданному варианту.
2. Определить токи в ветвях, используя метод контурных токов.
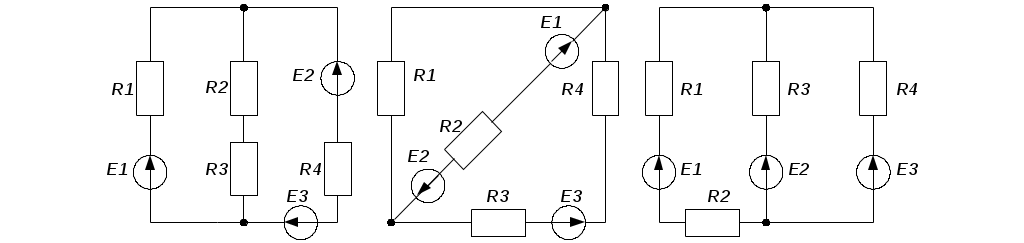
Рис. 3.13 Рис. 3.4 Рис. 3.15
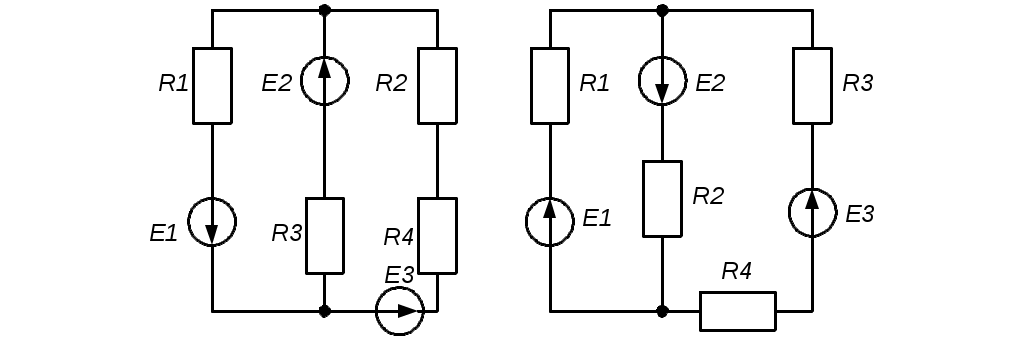
Рис. 3.16 Рис. 3.17
Таблица 3.2
| Вариант | Схема цепи | Элементы, входящие в электрическую цепь | ||||||
| Е1, В | Е2, В | Е3, В | R1, Ом | R2, Ом | R3, Ом | R4, Ом | ||
| 1 | 3.13 | 10 | 20 | 40 | 5 | 0 | 0 | 4 |
| 2 | 3.14 | 40 | 80 | 20 | 6 | 4 | 2 | 0 |
| 3 | 3.15 | 50 | 20 | 30 | 10 | 2 | 5 | 5 |
| 4 | 3.16 | 30 | 70 | 20 | 10 | 2 | 4 | 8 |
| 5 | 3.17 | 10 | 50 | 20 | 15 | 5 | 3 | 7 |
| 6 | 3.13 | 20 | 0 | 50 | 4 | 6 | 10 | 5 |
(продолжение табл. 3.2)
| 7 | 3.14 | 0 | 50 | 20 | 5 | 10 | 4 | 6 |
| 8 | 3.15 | 40 | 0 | 80 | 6 | 4 | 2 | 8 |
| 9 | 3.16 | 100 | 20 | 0 | 20 | 30 | 40 | 10 |
| 10 | 3.17 | 0 | 60 | 30 | 8 | 10 | 2 | 4 |
| 11 | 3.13 | 50 | 20 | 30 | 4 | 6 | 10 | 5 |
| 12 | 3.14 | 30 | 0 | 70 | 2 | 4 | 10 | 3 |
| 13 | 3.15 | 40 | 60 | 0 | 5 | 10 | 2 | 8 |
| 14 | 3.16 | 0 | 20 | 40 | 5 | 10 | 4 | 4 |
| 15 | 3.17 | 60 | 0 | 20 | 2 | 5 | 4 | 6 |
Контрольные вопросы
Дать определение узла, ветви, контура.
Сформулировать первый и второй законы Кирхгофа.
Каково соотношение между мгновенными значениями напряжений и токов на элементах R, L, C?
Записать выражение законов Кирхгофа в дифференциальной и комплексной форме.
Каков порядок составления системы уравнений по законам Кирхгофа?
6. Метод контурных токов. Каков порядок определения токов в ветвях?

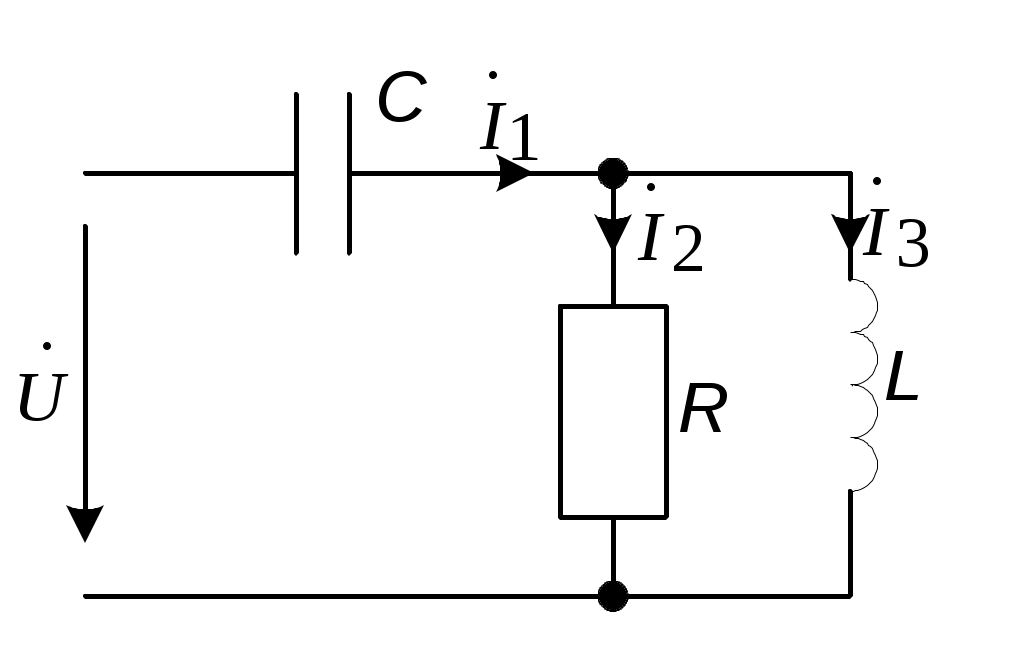 ис. 2.18
ис. 2.18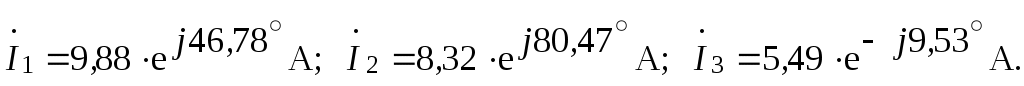
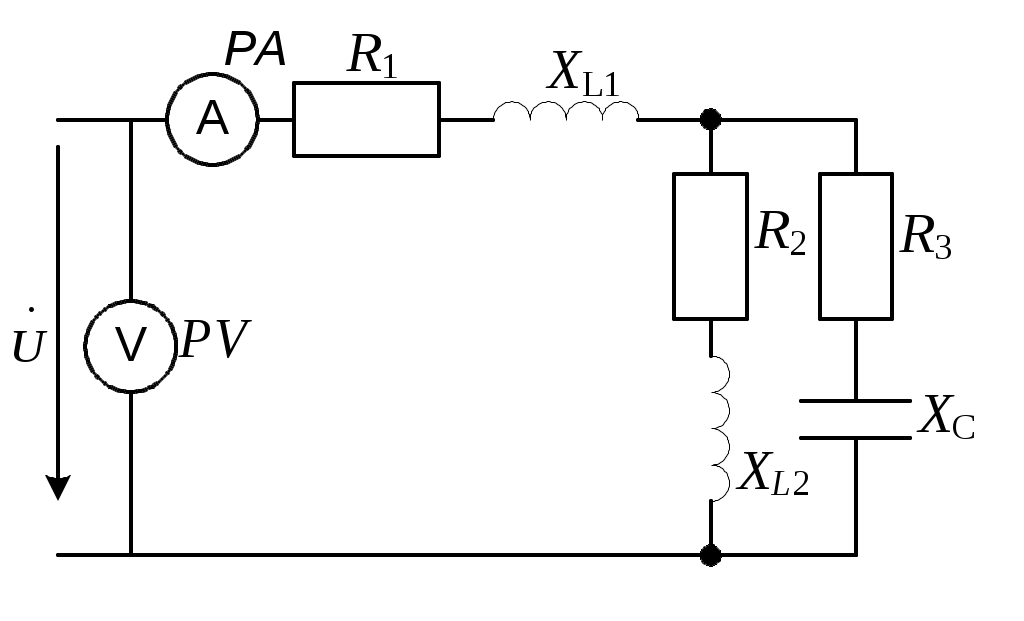 R1 = 7 Ом;R2 = 20 Ом;
R1 = 7 Ом;R2 = 20 Ом;