Электрических цепей постоянного тока

• Название: Электрических цепей постоянного тока
• Дата: 23.07.2022
• Размер: 5.4 Mb.
• Имя файла: materialy-dlya-dlya-studentov-fakulteta-elektrifikacii-po-podgot.doc
• Тип: Закон; #635135
• страница: 7 из 8

Тема 6

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ НЕСИНУСОИДАЛЬНЫХ ПЕРИОДИЧЕСКИХ ЭДС И НАПРЯЖЕНИЯХ

Цель: изучить методику расчета электрических цепей при несинусоидальных ЭДС, напряжениях, токах.

6.1. Задание по самоподготовке

1. 
   Проработать лекции по теме ”Электрические цепи при несинусоидальных периодических ЭДС ”.
   
2. 
   Изучить этот же материал по учебнику [1] § 7.1; 7.2; 7.6; 7.7; 7.8; 7.10; 7.11.
   
3. 
   Изучить методические указания по расчету цепей с несинусоидальными периодическими ЭДС п.6.2.
   
4. 
   Рассмотреть примеры п. 6.3; [1] 65, 69.
   
5. 
   Ответить на контрольные вопросы п. 6.6.
   

6.2 Общие сведения

Расчет токов в цепях при действии несинусоидальных периодических ЭДС производится следующим образом.

1. 
   Несинусоидальная периодическая ЭДС разлагается в ряд Фурье, то есть источник несинусоидальной периодической ЭДС представляют в виде последовательного соединения ряда источников с синусоидальными ЭДС и источника постоянной ЭДС.
   

е = е₀  +  е₁  +  е₂  +  е₃  +  …  +  е_k + ….

е₀ = Е₀ – постоянная составляющая ЭДС (нулевая гармоника).

Е_k = Е_kmsin(kw  +  ψ_k) – синусоидальная составляющая ЭДС (k –гармоника).

2. 
   Используя принцип наложения, рассчитывают токи в цепи от каждой ЭДС в отдельности. Ток постоянной составляющей рассчитывается методом расчета цепей постоянного тока. При этом имеют в виду, что индуктивность L не оказывает сопротивления постоянному току, а емкость С представляет бесконечно большое сопротивление постоянному току. Расчет токов от первой и последующих гармоник производится методом расчета синусоидальных цепей. Здесь уместно использовать комплексный метод. При этом индуктивные и емкостные сопротивления для k – ой гармоники равны соответственно и , где  –  угловая частота 1 – й гармоники.
   

В простейшем случае неразветвленной RLC цепи сопротивление для тока k – ой гармоники равно .

Результирующее мгновенное значение тока в цепи будет равно сумме мгновенных значений составляющих

3. 
   Действующее значение результирующего тока
   

где I_k  –  действующее значение тока k – ой гармоники;

I₀ – постоянный ток.

4. 
   Мощность при несинусоидальных ЭДС равна сумме мощностей отдельных гармоник
   

6.3 Пример

В электрической цепи (рис. 6.1) 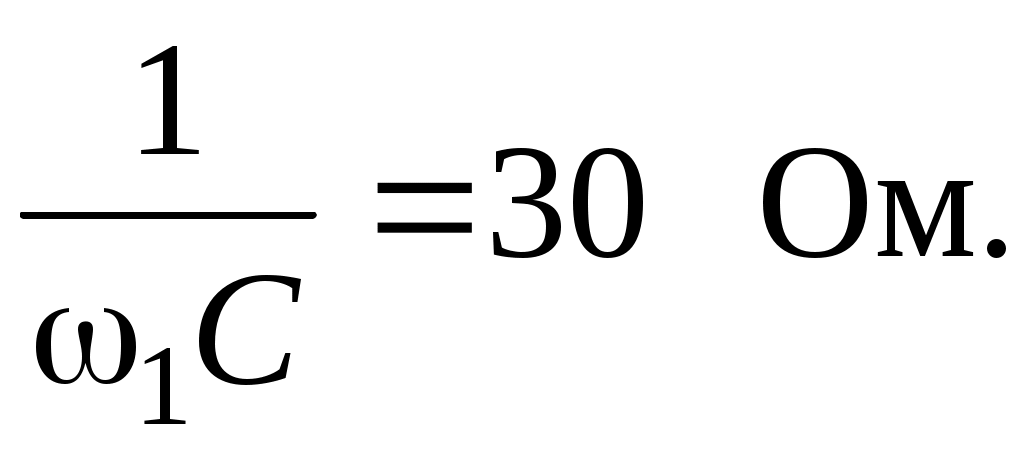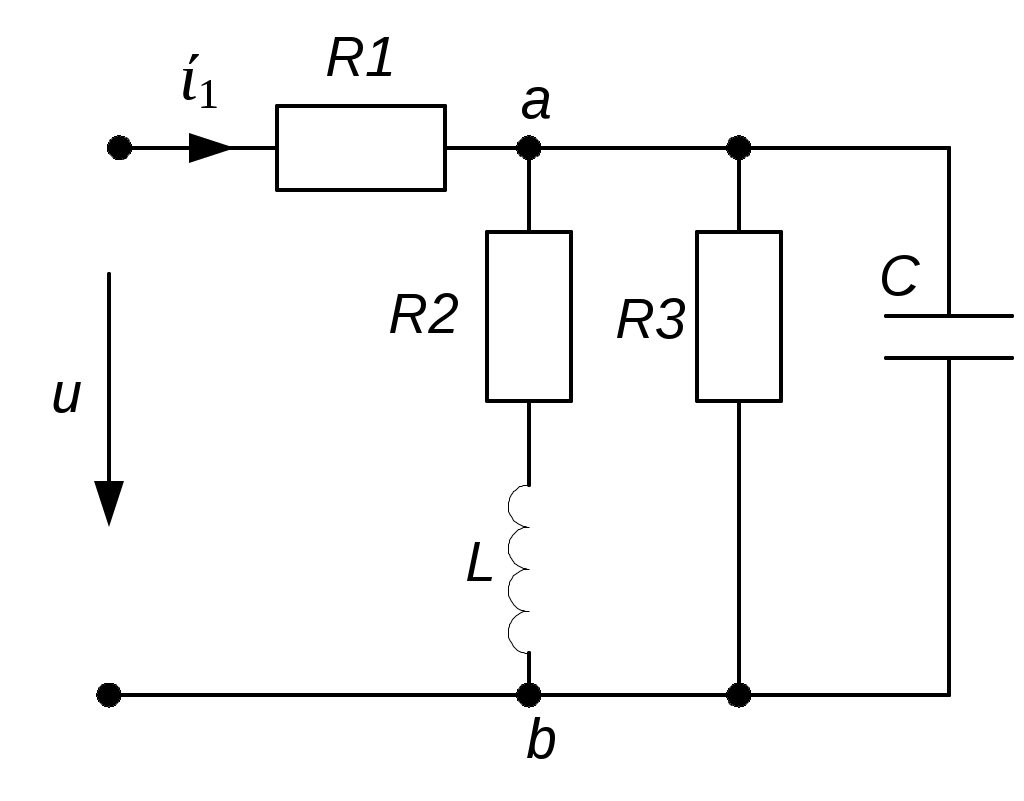R₁ = 6 Ом; R₂ = 5 Ом; R₃ = =20 Ом;



Рис. 6.1

Определить действующее и мгновенное значение тока в неразветвленной части. Вычислить мощность, расходуемую в цепи.

Решение

Расчет тока постоянной составляющей (нулевой гармоники):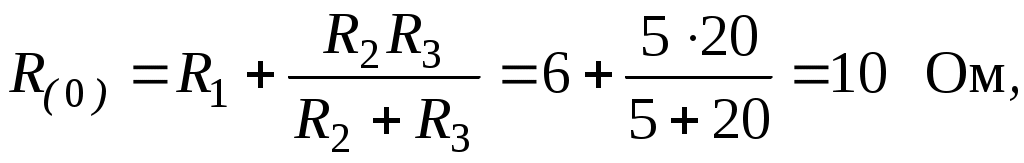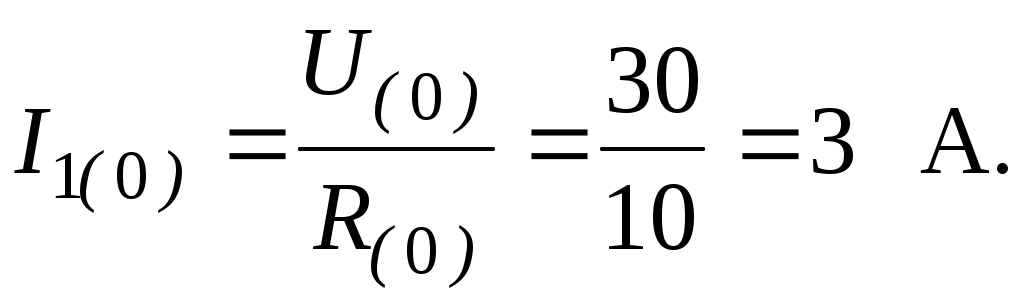





Расчет тока первой гармоники:

,







А,

А.

Расчет тока третьей гармоники:









=







Мгновенное значение тока в неразветвленной части цепи



Действующее значение тока



Мощность, расходуемая в цепи





,