Анализ ошибок спецификации модели.
Одной из основных ошибок, допускаемых при построении регрессионной модели, является ошибка спецификации (рис. 4.3). Под ошибкой спецификации понимается неправильный выбор функциональной формы модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1. Невключение в модель полезной (значимой) переменной.
2. Добавление в модель лишней (незначимой) переменной
3. Выбор неправильной функциональной формы модели
Последствия ошибки первого вида (невключение в модель значимой переменной) заключаются в том, что полученные по МНК оценки параметров являются смещенными и несостоятельными, а значение коэффициента детерминации значительно снижаются.
При добавлении в модель лишней переменной (ошибка второго вида) ухудшаются статистические свойства оценок коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели и затрудняет содержательную интерпретацию параметров, однако по сравнению с другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор функциональной формы модели, то есть допущена ошибка третьего вида, то получаемые оценки будут смещенными, качество модели в целом и отдельных коэффициентов будет невысоким. Это может существенно сказаться на прогнозных качествах модели.
Ошибки спецификации первого вида можно обнаружить только по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней является только одна переменная, осуществляется на основе расчета t - статистики для коэффициентов. При лишней переменной коэффициент будет статистически незначим.
Если же таких переменных несколько, целесообразно прибегнуть к сравнению значений коэффициентов детерминации модели до и после исключения из модели переменных, которые считаются лишними, при помощи расчета F-критерия.
Полученное значение сравнивается с критическим F α;m1–m2;n–m1–1. Если расчетное значение меньше, то считается, что исключенные из модели переменные являются лишними.
Ошибки третьего вида можно обнаружить только при помощи содержательной интерпретации модели или визуально анализируя данные или по наличию гетероскедастичности.
Комплексный анализ ошибок спецификации можно провести, выполнив один или несколько из следующих тестов:
1) Тест Рамсея (Regression specification error test – RESET);
2) Тест максимального правдоподобия (The Likelihood Ratio test);
3) Тест Валда (The Wald test);
4) Тест множителя Лагранжа (The Lagrange multiplier test);
5) Тест Хаусманна (The Hausmann test)
6) Преобразование Бокса-Кокса (Box-Cox transformation)
Методы линеаризации нелинейных моделей.
Линеаразиция - один из наиболее распространенных методов анализа нелинейных систем. Идея линеаризации - использование линейной системы для аппроксимации поведения решений нелинейной системы в окрестности точки равновесия. Линеаризация позволяет выявить большинство качественных и особенно количественных свойств нелинейной системы.
Методы линеаризации имеют ограниченный характер, то есть эквивалентность исходной нелинейной системы и ее линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, или для определенных процессов, причем, если система переходит из одного режима работы в другой, то следует изменить и ее линеаризованную модель.
Рассмотрим такие методы линеаризации нелинейных моделей, как замена переменных; логарифмирование обеих частей уравнения и комбинированные методы. Суть первого метода состоит в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Например, полиномиальная модель которого порядка может быть приведена к линейному виду путем замены переменных.
Среди нелинейных полиномиальных регрессионных моделей чаще всего используются параболические модели второго и третьего порядка. Ограничения в использовании полиномов более высоких порядков связаны с содержательной интерпретацией коэффициентов регрессии.
Линеаризация системы нелинейных уравнений в окрестности точки равновесия может быть достигнута путем замены переменных так, чтобы точка равновесия превратилась в начало координат. Уравнения, полученные в результате указанного действия, будут линейными и называться линеаризацией исходной системы. Точки исходной системы, находящиеся в окрестности точки равновесия, будут соответствовать точкам в окрестности начала координат новой системы. Нас будет интересовать:
значение новых переменных, близкие к нулю;
при каких условиях нелинейными выражениями можно пренебречь.
Замену переменных можно использовать и при другой организации линеаризации. Производят замену: 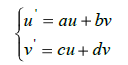 где где 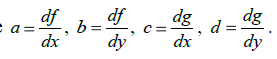 Это может быть записано в виде: Это может быть записано в виде: 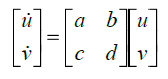 где где 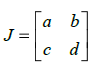 называется якобиан. называется якобиан.
| Временные ряды: аддитивные и мультипликативные модели тренда и сезонности.
В теории временных рядов чаще всего применяются два способа записи моделей временных рядов. Первый способ основывается на предположении, что влияние всех его компонент на значения элементов временного ряда носит аддитивный характер. В этом случае модель временного ряда называется аддитивной и имеет вид
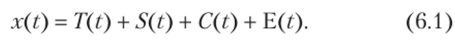
Второй способ записи модели основан на предположении о мультипликативном характере воздействия компонент временного ряда на x(t). В этом случае модель временного ряда называется мультипликативной и записывается в виде произведения: 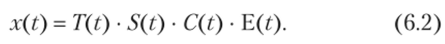
Выбор в пользу аддитивной или мультипликативной модели осуществляется на основе анализа динамики временного ряда. Если периодические колебания значений временного ряда имеют относительно постоянную амплитуду, то предпочтительнее использовать аддитивную модель.
Мультипликативную модель логичнее использовать в ситуациях, когда амплитуда колебаний изменяется с течением времени. Такими свойствами, как правило, обладают развивающиеся экономические процессы.
Пример такого процесса — динамика инвестиций в основной капитал в Российской Федерации.
Далее будем рассматривать анализ только аддитивной модели, так как мультипликативная модель может быть сведена к аддитивному виду посредством логарифмирования левой и правой частей. Отметим также, что присутствие в модели всех четырех компонент не является обязательным. Например, временной ряд может не содержать тренда или циклических колебаний. Единственная компонента, которая всегда присутствует в модели временного ряда, — это случайная функция Е.
Процесс анализа временного ряда предполагает последовательное выполнение следующих этапов.
Этап 1. Определение структуры временного ряда, т.е. формирование набора неслучайных функций, которые должны присутствовать в разложении.
Этап 2. Оценивание неслучайных функций, присутствие которых в модели было доказано на первом этапе.
Этап 3. Построение модели для Е(?)> описывающей влияние случайных факторов (построение модели остатков).
Простейшую ситуацию для анализа представляет собой модель, содержащая только случайную компоненту. Построение таких моделей, как правило, проводится в рамках теории стационарных временных рядов.
| Системы одновременных эконометрических уравнений.
Не всегда получается описать адекватно сложное социально-экономическое явление с помощью только одного соотношения (уравнения). Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить, какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений.
В любой эконометрической модели в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:
Экзогенные (независимые) – значения которых задаются «извне», автономно, в определенной степени они являются управляемыми (планируемыми) (X). Экзогенные переменные модели характеризуются тем, что они являются независимыми и определяются вне системы;
Эндогенные (зависимые) - значения которых определяются внутри модели, или взаимозависимые (Y).
Лаговые – экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Например:
yt – текущая эндогенная переменная,
yt-1 – лаговая эндогенная переменная (отстоящая от текущей на 1 период назад),
yt-2 – тоже лаговая эндогенная переменная (отстоящая от текущей на 2 периода).
Динамические модели экономики содержат в правой части лаговые переменные, а также учитывают тенденцию.
Предопределенные переменные – переменные, определяемые вне модели. К ним относятся лаговые и текущие экзогенные переменные (xt , xt-1), а также лаговые эндогенные переменные (yt-1).
Все эконометрические модели предназначены для объяснения текущих значений эндогенных переменных по значениям предопределенных переменных.
В дальнейшем для простоты будем рассматривать в качестве предопределенных переменных только текущие экзогенные переменные (х).
| Динамические эконометрические модели.
Теперь рассмотрим модели временных рядов, где в качестве исходных статистических данных мы располагаем наблюдениями двух временных рядов: *1, *2, •?•> х„ иуь У2,уЦелью регрессионного анализа в данном случае является построение линейной регрессионной модели, позволяющей с наименьшими ошибками прогнозировать значения у, по значениям х, для t > п.
Подобные модели естественны в ситуациях, когда две переменные х и у связаны так, что воздействия единовременного изменения одной из них (х) на другую (у) сказываются в течение достаточно продолжительного времени, т.е. наблюдается распределенный во времени эффект воздействия. В частности, такие связи возникают между регистрируемыми во времени входными и выходными характеристиками процессов накопления и распределения ресурсов (например, процессов преобразования доходов населения в его расходы) или процессов трансформации затрат в результаты (например, процессов воспроизводства основных доходов).
Эконометрическая модель является динамической, если в данный момент 1 она учитывает значения входящих в нее переменных, относящихся как к текущему, так и к предыдущим моментам времени, т.е. модель учитывает, отражает динамику исследуемых переменных в каждый момент времени.
Переменные, влияние которых характеризуется определенным запаздыванием, называются лаговыми переменными.
Динамические модели классифицируются по-разному. Приведем один из вариантов классификации.
1. Модели с распределенными лагами. Они содержат в качестве ла- говых переменных лишь независимые (объясняющие) переменные, например:
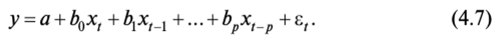
2. Авторегрессионные модели, уравнения которых включают в качестве объясняющих переменных лаговые значения зависимых переменных, например:
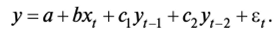
Рассмотрим модель (4.7), приняв, что р — конечное число. Модель говорит о том, что, если в некоторый момент t происходит изменение
x, это изменение будет влиять на значение у в течение р последующих моментов времени. Коэффициент Ь0 называется краткосрочным мультипликатором, так как он характеризует изменение среднего значения
у при единичном изменении х в тот же самый момент. Сумма 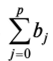 называется долгосрочным мультипликатором, который характеризует изменение у под воздействием единичного изменения х в каждом из моментов времени. Любая сумманазывается промежуточным называется долгосрочным мультипликатором, который характеризует изменение у под воздействием единичного изменения х в каждом из моментов времени. Любая сумманазывается промежуточным
мультипликатором. 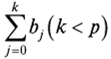
Относительные коэффициенты модели (4.7) с распределенным лагом определяются выражениями:
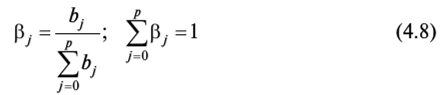
(условие нормировки имеет место, только если все bj имеют одинаковые знаки). Значения ру в (4.8) являются весами для соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения
y, приходящегося на момент (/ + j).
|
|
 Скачать 338.27 Kb.
Скачать 338.27 Kb.