Эконометрика. Этапы вероятностностатистического моделирования. 4
 Скачать 338.27 Kb. Скачать 338.27 Kb.
|
Классы нелинейных моделей.Значение свойства линейности и связанного с ним принципа суперпозиции отмечено в разд. 4.1. В случае линейной модели знания одной функции времени, характеризующей объект (весовой функции), достаточно для определения выходного сигнала объекта при произвольных входных сигналах. Это обеспечивает преимущества, которые хотелось бы сохранить и при описании нелинейных объектов, а именно: 1) возможность явно записать связь между входом и выходом; 2) простота описания соединений систем; 3) возможность рассмотрения случайных сигналов. Для некоторых классов нелинейных объектов эти требования выполняются при использовании рядов Вольтерра. Разложение Вольтерра Используя ряды Вольтерра, ядра которых представляют собой весовые функции высших порядков, можно получить описание нелинейного объекта, допускающее ясную физическую интерпретацию. Этот метод имеет большое достоинство, связанное с тем, что нелинейная система рассматривается как непосредственное обобщение линейного случая, хотя сам объект может существенно отличаться от лилейного. Иначе говоря, метод с использованием рядов Вольтерра интерпретирует линейные объекты как подкласс нелинейных объектов. Это достоинство вряд ли можно переоценить, так как на временной и спектральный анализ линейных систем затрачено немало времени и усилий, а ряды Вольтерра позволяют использовать накопленные знания для исследования нелинейных систем. Анализ и синтез с помощью рядов Вольтерра является наиболее удобным из существующих методов изучения нелинейных систем. Изложению этого метода посвящена обширная литература. Рассмотрим нелинейный объект с памятью. Пусть и 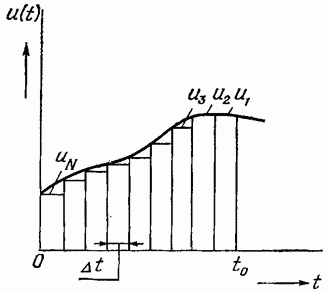 Фиг. 4.4. конечна, т. е. величина и 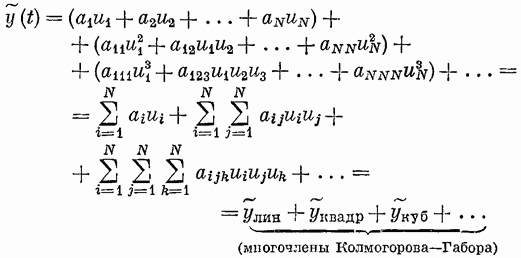 Начальные условия предполагаются нулевыми. При выполнении этих условий и если Если все 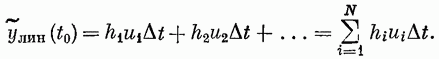 Учитывая порядок нумерации 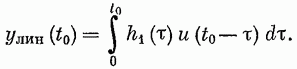 При подаче на систему двух импульсов вид линейного члена разложения определяется принципом суперпозиции: Если учесть квадратичные члены или члены более высоких порядков, то становится очевидным взаимодействие двух импульсов. Пусть В пределе уквадр принимает вид 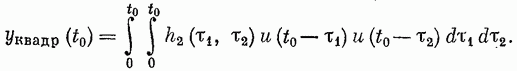 Таким образом, преобразуется в ряд Вольтерра вида 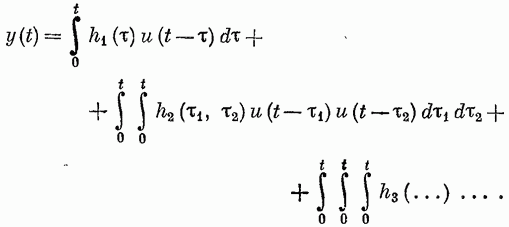 Таким образом, разложение в ряд Вольтерра является непосредственным обобщением модели линейного объекта в форме интеграла свертки. Весовая функция Функция 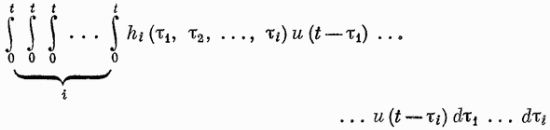 называется функционалом 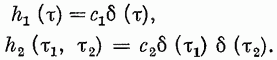 Тогда функциональный ряд принимает вид Ниже будет показано, что поведение степенного ряда определяет характер нелинейности. В некоторых случаях, используя степенные ряды, можно исследовать сходимость ряда Вольтерра. Если перейти к ряду Вольтерра с бесконечным числом членов, то по теореме Фреше функциональным степенным рядом можно описать связь между входом и выходом произвольного непрерывного нелинейного объекта. Функциональный ряд единствен и сходится при Ядра рядов Вольтерра для физически реализуемых объектов обладают следующими свойствами: 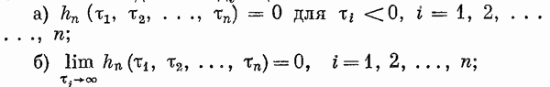 Первые два свойства тривиальны. Выходной сигнал физически реализуемой системы зависит только от предыстории входного сигнала. Все устойчивые объекты имеют конечную память, так что для больших Перейдем к третьему свойству. Ядра являются симметричными или могут быть представлены в симметричном виде циклической перестановкой аргументов несимметричного ядра. Покажем это для двумерного случая на примере Левое и правое выражения не равны между собой, но если проинтегрировать эти выражения в одних и тех же пределах по первому квадранту плоскости та), то величина интеграла 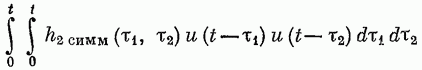 совпадает с интегралом 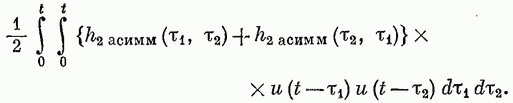 Таким образом, в общем случае симметризация проводится по формуле 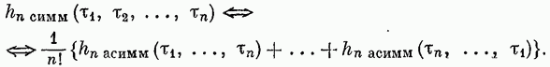 Определение ядер по дифференциальным уравнениям. В принципе эту задачу можно решить, подставляя ряд Вольтерра для  где дифференциального уравнения Эта процедура здесь не воспроизводится, так как она достаточно трудоемка, особенно для более сложных дифференциальных уравнений. Удобнее воспользоваться методом многомерного преобразования Лапласа. Использование преобразования Лапласа. Многомерное преобразование Лапласа определяется следующей формулой: 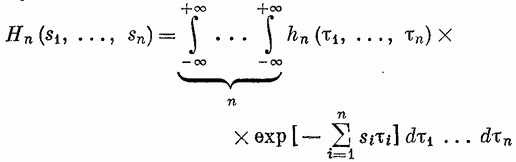 и называется преобразованием Лапласа 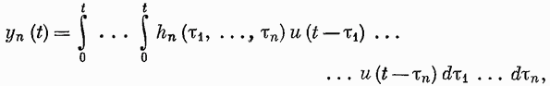 введем новые переменные и то  Теперь функцию довольно трудоемок, и лучше воспользоваться методом группировки переменных [22], который устанавливает связь между 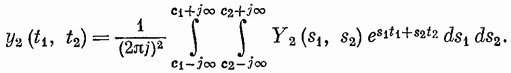 Положим 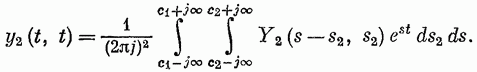 Следовательно, 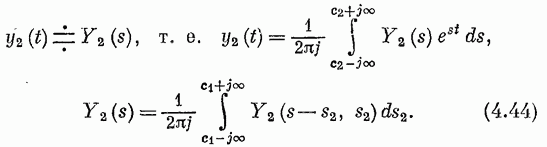 В пространстве  Объекты с линейными звеньями и множительными устройствами хорошо описываются рядами Вольтерра. Вид ядер можно непосредственно определить из структуры такого нелинейного объекта. Это оказывается полезным при решении задачи определения ядер, удовлетворяющих дифференциальному уравнению. Кроме того, в этом случае по ядрам легче строить модель объекта. |
