Эконометрика. Этапы вероятностностатистического моделирования. 4
 Скачать 338.27 Kb. Скачать 338.27 Kb.
|
Основные виды уравнений регрессий. Сравнительный анализ, особенности выбора.Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки. Линейная регрессия Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой. Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом: Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b Где a_n — это коэффициенты, X_n — переменные и b — смещение. Полиномиальная регрессия Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное: Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже. Гребневая (ридж) регрессия В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями: Коэффициент регрессии не важен, несмотря на то, что, теоретически, переменная должна иметь высокую корреляцию с Y. При добавлении или удалении переменной из матрицы X, коэффициент регрессии сильно изменяется. Переменные матрицы X имеют высокие попарные корреляции (посмотрите корреляционную матрицу). Регрессия по методу «лассо» В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения: min || Xw — y ||² + z|| w || Регрессия «эластичная сеть» Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов. min || Xw — y ||² + z_1|| w || + z_2|| w ||² Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных. |
Понятие мультиколлениарности объясняющих переменных.Мультиколлинеарностью называется высокая степень коррелированное™ двух или нескольких объясняющих переменных в уравнении множественной регрессии. Крайним случаем мультиколлинеарности является линейная зависимость между объясняющими переменными. Считается, что две переменные X,- и X сильно коррелированы, если выборочный коэффициент корреляции двух объясняющих переменных гхх. >0,7. Рассмотрим виды мультиколлинеарности. 1. Строгая мультиколлинеарность — наличие линейной функциональной связи между объясняющими переменными (иногда также линейная связь с зависимой переменной). Связь между объясняющими переменными — функциональная. Строгая мультиколлинеарность не позволяет однозначно определить коэффициенты регрессии bt и bj и разделить вклады объясняющих переменных Xj и Xj в зависимую переменную У. 2. Нестрогая мультиколлинеарность — наличие сильной линейной корреляционной связи между объясняющими переменными (иногда также и зависимой переменной). При нестрогой мультиколлинеарности связь между объясняющими переменными корреляционная. Сложность проблемы мультиколлинеарности состоит в следующем. 1. Корреляционные связи есть всегда. Проблема мультиколлинеарности — сила проявления корреляционных связей. 2. Однозначных критериев определения мультиколлинеарности не существует. 3. Строгая мультиколлинеарность нарушает предпосылку 5 теоремы Гаусса — Маркова и делает построение регрессии невозможным (см. гл. 4, параграф 4.1), так как согласно теореме Кронекера — Капелли система уравнений имеет бесчисленное множество решений. 4. Нестрогая мультиколлинеарность затрудняет работу, но не препятствует получению правильных выводов. Поясним сказанное о проблеме мультиколлинеарности. Пусть имеется т объясняющих факторов Х{, Х2, ..., Хт. Матрица межфакторной корреляции состоит из парных коэффициентов корреляции и имеет вид 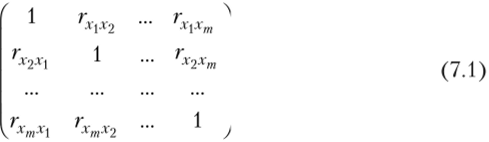 Парный коэффициент корреляции гх.х. определяется по формуле1 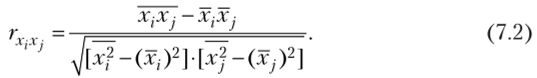 Отметим, что так как rxx = 1, i = 1,2,..., т, и гх х. = гх х., то данная матрица является симметрической. Если связь между факторами полностью отсутствует, то недиагональные элементы матрицы межфакторной корреляции будут равны нулю, а ее определитель будет равен единице: | Rxx = 1. |
