|
|
Фазовый переход жидкость твердое тело
Теория фазовых переходов
Фазовый переход «жидкость – твердое тело». Энергетические условия процесса кристаллизации. Механизм процесса. Формирование зародыша. Форма кристаллов и их поверхности. Строение слитка. Методы выращивания кристаллов. Методы исследования кристаллов.
Фазовый переход «жидкость – твердое тело».
Фазовый переход (фазовое превращение) - переход между различными макроскопичными состояниями (фазами) многочастичной системы, происходящий при определенных значениях внешних параметров (температуры Т, давления Р, магнитного поля Н и т. п.) в т. н. точке перехода. Ф. п. следует отличать от постепенных превращений одного сост. в другое (напр., ионизация атомарного или молекулярного газа и превращение его в плазму), происходящих в целом интервале параметров, иногда такие превращения наз. Ф. п. в широком смысле слова.
Ф. п.- кооперативные явления, происходящие в системах, состоящих из большого (строго говоря, бесконечного) числа частиц. Ф. п. происходят как в равновесных термодинамических системах (напр., Ф. п. из парамагнитного в ферромагнитное состояние при понижении температуры), так и в системах, далёких от термодинамического равновесия (напр., переход лазера в состояние когерентной генерации при увеличении уровня накачки). Далее (если не оговорено особо) обсуждаются Ф. п. в равновесных системах.
Обычно различают Ф. п. 1-го рода, происходящие с выделением или поглощением теплоты и сопровождающиеся скачками уд. объёма, и Ф. п. 2-го рода, происходящие непрерывным образом, но сопровождающиеся аномальным возрастанием флуктуа-ционных явлений.
Ф. п. 1-го рода. Точка Ф. п. 1-го рода характеризуется равенством уд. Гиббса энергий (термодинамических потенциалов) двух фаз, между которыми происходит переход: Ф1(Т,Р,Н) = = Ф2(Т, Р, Н). При этом производные термодинамических потенциалов Ф1,2 по параметрам Т, Р... (т. е. энтропия, уд. объём и т. п.), вообще говоря, не совпадают. Поэтому Ф. п. 1-го рода связаны со скачкообразными изменениями этих величин. В некоторой окрестности точки Ф. п. 1-го рода в обеих фазах реализуются локальные минимумы термодинамических потенциалов; одна из фаз является абсолютно устойчивой, а другая – метастабильной. Для каждой из фаз, рассматриваемых по отдельности, точка Ф. п. 1-го рода ничем не выделена, в частности процессы установления термодинамического равновесия не испытывают замедления в окрестности этой точки, в то время как процесс превращения одной фазы в другую резко замедляется. Поэтому для Ф. п. 1-го рода характерны явления гистерезиса (напр., переохлаждение и перегрев), когда первоначально стабильная фаза при прохождении точки равновесия фаз сохраняется как метастабильная в некотором интервале параметров. В точке равновесия обе фазы могут сосуществовать бесконечно долго, в этом случае имеет место т. н. фазовое расслоение.
Примером расслоения является сосуществование жидкости и её пара (или твёрдого тела и расплава) в условиях заданного полного объёма системы. Условие сосуществования фаз при расслоении - равенство хим. потенциалов этих фаз. Хим. потенциал m (T, P, ...) определяется как удельный (приходящийся на одну частицу) термодинамический потенциал m=Ф/N. В эднокомпонентной системе две фазы находятся в равновесии на некоторой кривой в плоскости Р, Т, определяемой условием 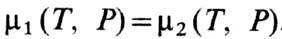 . Вид кривой Т(Р) связан с уд. теплотой Ф. п. q и скачком уд. объёма Du (Клапейрона-Клаузиуса уравнение):
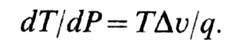
Макс. число сосуществующих фаз для однокомпонентной системы равно 3 (газ, жидкость, твёрдое тело). Для системы из п независимых компонентов (раствора) макс. число сосуществующих фаз r определяется Гиббса правилом фаз: r=n+2
Ф. п. 1-го рода широко распространены в природе. К ним относятся испарение и конденсация, плавление и кристаллизация. Структурный переход графита в алмаз при высоком давлении, опрокидывание подрешёток антиферромагнетиков во внешнем магнитном поле и др. Примерами низкотемпературных Ф. п. 1-го рода могут служить разрушение сверхпроводимости чистых сверхпроводников сильным магнитном полем, затвердевание 4Не2 под давлением.
Ф. п. 2-го рода. Точка Ф. п. 2-го рода является особой для термодинамических величин системы; при прохождении этой точки первоначально устойчивая фаза более не соответствует никакому (даже метастабильному) минимуму свободной энергии и потому не может существовать. Явления перегрева и переохлаждения при Ф. п. 2-го рода отсутствуют. Примерами Ф. п. 2-го рода являются переходы в точке Кюри в ферромагнитной или сегнетоэлектрической фазы, l - переход 4Не2 в сверхтекучее состояние. Ф. п. металлов в сверхпроводящее состояние в нулевом магнитном поле. Особым видом Ф. п. 2-го рода являются критические точки системы жидкость - пар или аналогичные им критические точки растворов. Ф. п. 2-го рода характеризуются аномальным возрастанием величин, характеризующих отклик системы на внеш. воздействия,- обобщённых восприимчивостей. Так, вблизи точек Кюри ферромагнетиков и сегнетоэлектриков резко возрастают магнитные и диэлектрические восприимчивости; вблизи критической точки жидкость-пар аналогичный рост испытывает сжимаемость.
Вблизи точек Ф. п. 2-го рода наблюдается также аномальный рост флуктуации. Так, флуктуации плотности вблизи критической точки приводят к усилению рассеяния света (опалесценция критическая), вблизи магнитных фазовых переходов усиливается рассеяние нейтронов на флуктуациях магнитных моментов, структурные фазовые переходы 2-го рода в кристаллах сопровождаются аномальным рассеянием рентгеновских лучей. При флуктуационных явлениях вблизи Ф. п. 2-го рода резко замедляются процессы установления равновесия в системе.
Изменение состояния системы при Ф. п. 2-го рода можно описать как изменение её симметрии (напр., переход кристалла из фазы с кубической симметрией в тетрагональную). Связь между Ф. п. 2-го рода и изменением симметрии системы лежит в основе общей теории Ф. п. Для количественного описания изменения симметрии в этой теории вводят понятие параметра порядка, в качестве которого выбирают величину, линейно преобразующуюся под действием группы симметрии системы (напр., магн. момент в ферромагнетике, волновая флуктуация бозе-конденсата в 4Не2). Термодинамическое среднее параметра порядка равно нулю в одной из фаз (более симметричной) и непрерывно возрастает от нулевого значения в другой. Изменение симметрии при Ф. п. 2-го рода связано с неустойчивостью симметричного состояния и носит название спонтанного нарушения симметрии. Теория Ландау является теорией самосогласованного поля; условием ее применимости является малость Гинзбурга числаGi, что выполняется в чистых сверхпроводниках 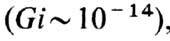 в ряде сегнетоэлектриков и в некоторых других системах с эффективным дальнодействием. В этих случаях при Ф. п. 2-го рода наблюдается скачок теплоёмкости, причём большей теплоёмкостью обладает несимметричная (упорядоченная) фаза. При Gi>1 теория Ландау неприменима; в частности, это относится к Ф. п. в сверхтекучее состояние, когда теплоёмкость С аномально растёт при температурах Т, близких к критической темп-ре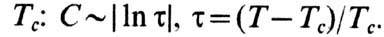
Существующие отклонения от теории Ландау возникают также в системах с Gi<<1 в непосредственной окрестности точки перехода (|t|<Gi), называемой флуктуационной областью (при Gi1 флуктуационной является вся окрестность Ф. п. 2-го рода). Во флуктуационной области термодинамические (а также кинетические) характеристики системы испытывают аномалии, которые обычно описывают степенными законами с нецелыми показателями. Критические показатели (КП) обладают свойством универсальности, т. е. не зависят от физ. природы вещества и даже от физ. природы Ф. п., а определяются типом спонтанного нарушения симметрии (так, КП сверхтекучего Ф. п. совпадают с КП ферромагнетиков. Ф. п. в магнетике с анизотропией типа "лёгкая плоскость"). Вычисление этих КП, как и выяснение общих закономерностей Ф. п. 2-го рода вне области применимости теории Ландау, является предметом флуктуационной теории Ф. п. 2-го рода. В этой теории (основанной, как и теория Ландау, на понятии спонтанного нарушения симметрии) аномальное поведение физ. величин вблизи Тс связывается с сильным взаимодействием флуктуации параметра порядка. Радиус корреляции Rc этих флуктуаций растёт с приближением к точке Ф. п. и обращается в бесконечность при Т=Тс. Поэтому оказывается невозможным разделить систему на статистически независимые подсистемы, в силу чего флуктуации на всех пространственных масштабах оказываются существенно негауссовыми.
Масштабная инвариантность. В точке Ф. п. 2-го рода аномально усиливаются флуктуации не только параметра порядка, но и ряда др. величин (к ним относятся, в частности, плотность энергии, тензор напряжений и некоторые другие). Все вместе они образуют набор аномально флуктуирующих величин Ai. Задача теории - вычисление корреляционных функций величин Аi(х), через которые выражаются аномальные вклады в термодинамические величины. Центральным для флуктуационной теории является представление омасштабной инвариантности флуктуации в точке Ф. п. Масштабная инвариантность означает отсутствие в системе к--л. характерного пространств, масштаба, превышающего масштаб постоянной решётки; иначе говоря, на всех пространств. масштабах флуктуации ведут себя подобным образом. Это означает, что подобное изменение всех расстояний |xi-xj| , больших по сравнению с постоянной решётки и входящих в к--л. корреляционную функцию , сводится к изменению единицы длины, причём одновременно изменяются и единицы измерения полей Аi(х). Каждая величина Аi(х) характеризуется своим размерным показателем (индексом) DA в преобразовании подобия:
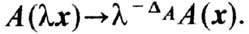
Это соотношение является математическим выражением гипотезы подобия (масштабной инвариантности) флуктуации в точке Ф. п. 2-го рода. Подчеркнём, что размерные показатели DA не совпадают с обычными физ. размерностями величин А, поскольку в их определение входят размерные микроскопические параметры, не влияющие на свойства аномальных флуктуации и не меняющиеся при масштабных преобразованиях.
Масштабная инвариантность позволяет определить вид парных корреляционных функций c точностью до констант:
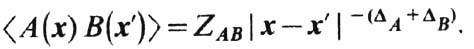
В окрестности Ф. п. 2-го рода флуктуации характеризуются единственным размерным параметром - радиусом корреляции Rс. Все термодинамические величины, характеризующие Ф; п. 2-го рода (точнее, их аномальные части), оказываются степенными функциями Rc. Из соотношений подобия можно найти общий вид корреляций функций вблизи Тс:
Фурье-компоненты этих функций определяют структурные факторы аномального рассеяния вблизи Тс (напр., рассеяния света вблизи критической точки или рассеяния нейтронов в ферромагнетиках):
Здесь q-волновой вектор рассеяния, f(x) - безразмерная функция с асимптотиками
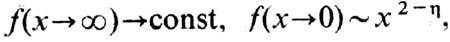
где h - критический показатель. Соотношение (*) даёт возможность единым образом представить эксперим. данные, относящиеся к разл. интервалам q и Rc. Экспериментально соотношения (*) хорошо выполняются в самых разл. Ф. п. 2-го рода, что подтверждает гипотезу масштабной инвариантности.
Количеств. вычисления КП и обоснование картины скейлинга связаны с применением методов ренормализационной группы иэпсилон-разложения. Метод ренормгруппы состоит в последовательном усреднении по всевозможным флуктуациям с пространств. масштабами, меньшими некоторого l, при фиксир. крупномасштабных конфигурациях. Изменяя затем единицы измерения длин (и соответствующим образом единицы флуктуирующих полей), возвращаемся к системе с теми же линейными размерами, но несколько изменённым функционалом свободной энергии. Такое преобразование наз. п р е о б р а з о в а н и е м р е н о р м и р о в к и. Условие неизменности функционала свободной энергии при последовательном проведении ренормировки и увеличении масштаба l до бесконечности определяет точку Ф. п. 2-го рода. Именно существование такой неподвижной точки в пространстве возможных функционалов, отвечающих Ф. п. 2-го рода с заданным типом нарушения симметрии, подтверждает гипотезу масштабной инвариантности. КП вычисляют с помощью линеаризации ур-ний ренормгруппы вблизи неподвижной точки. Вычисление КП для Ф. п. 2-го рода в трёхмерных системах проводится обычно с помощью формального рассмотрения систем размерности 4-e, где e<<1 (т. н. эпсилон-разложение) с последующим продолжением до e=1. Найденные таким способом КП находятся в хорошем согласии с эксперим. данными. Для Ф. п. 2-го. рода в двумерных системах часто удаётся найти точные значения КП.
Необычные Ф. п. В ряде двумерных систем Ф. п. 2-го рода не связан с появлением макроскопич. параметра порядка, но приводит к качеств. изменению свойств системы. Это относится, в частности, к переходам в сверхтекучее и сверхпроводящее состояния в тонких плёнках, где появляется ненулевая сверхтекучая плотность в отсутствие бозе-конденсата. Отсутствие макроскопич. параметра порядка связано в этих случаях с аномально сильными флуктуациями в упорядоченной фазе. Особый класс Ф. п. 2-го рода представляют собой Ф. п. в неупорядоченных системах (напр., в спиновых стёклах). С точки зрения макроскопич. симметрии фаза спинового стекла неотличима от соответств. высокотемпературной (парамагн.) фазы. Физ. отличие этих фаз связано с появлением в фазе спинового стекла неубывающих во времени автокорреляц. ф-ций локализованных магн. моментов
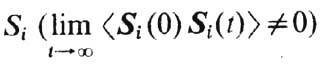
при нулевом полном моменте системы. Для Ф. п. в состояние спинового стекла характерно отсутствие наблюдаемых аномалий теплоёмкости и резкий рост времени магн. релаксации. Последовательное теоретич. описание таких Ф. п. отсутствует.
Различие между Ф. п. 1-го рода и 2-го рода является несколько условным, т. к. нередко наблюдаются Ф. п. 1-го рода с малой теплотой перехода и сильными флуктуациями, характерными для Ф. п. 2-го рода. К ним относятся большинство Ф. п. между разл. мезофазами жидких кристаллов, нек-рые структурные Ф. п., а также многие Ф. п. в антиферромагн. состояния со сложной магн. структурой. В последнем случае, как и в нек-рых других, существование Ф. п. 1-го рода связано с сильным взаимодействием флуктуации; по теории Ландау эти переходы должны быть Ф. п. 2-го рода. Существуют также примеры противоположного типа: по теории Ландау все фазовые переходы плавления должны быть Ф. п. 1-го рода, однако в ряде двумерных систем с сильно развитыми флуктуациями эти переходы оказываются Ф. п. 2-го рода.
В ряде случаев движение вдоль кривой Ф. п. 1-го рода при изменении внеш. параметров приводит к уменьшению теплоты перехода и скачка уд. объема вплоть до полного их исчезновения, после чего Ф. п. между теми же фазами происходит как Ф. п. 2-го рода. Соответствующая точка на кривой перехода наз. трикритической точкой, она характеризуется резкой аномалией теплоёмкости в упорядоченной фазе: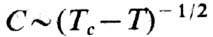 . Вблизи трикритич. точки флуктуации столь же сильны, как вблизи любой точки Ф. п. 2-го рода, однако их взаимодействие между собой аномально слабое. Это позволяет применять для описания трикритич. точки теорию самосогласованного поля.
|
|
|
Скачать 0.54 Mb.