тема гигиена. Тема 1 08.02.-12.02. Физическое развитие детей и подростков. Методика исследования физического развития, медицинская антропометрия, разработка стандартов физического развития и оценочных таблиц

• Название: Физическое развитие детей и подростков. Методика исследования физического развития, медицинская антропометрия, разработка стандартов физического развития и оценочных таблиц
• Анкор: тема гигиена
• Дата: 24.10.2021
• Размер: 1.63 Mb.
• Имя файла: Тема 1 08.02.-12.02.doc
• Тип: Закон; #254913
• страница: 5 из 5

УЧЕБНАЯ ИНСТРУКЦИЯ

по методике гигиенической оценки состояния здоровья и физического развития организованного детского коллектива
Сравнительная оценка уровня физического развития разных коллективов или одного и того же коллектива в динамике обучения в современной школе осуществляется на основании определения разницы величин основных показателей состояния здоровья и физического развития путем применения методов сравнения средних арифметических величин, распределения относительных чисел и квадратических отклонений, а также на основании корреляционного метода.

Следует отметить, что в ходе использования метода сравнения средних арифметических величин сопоставлению подлежат показатели состояния здоровья и физического развития лишь однородных взрастно–половых групп. При этом, прежде всего, необходимо установить достоверность отличий средних величин сравниваемых групп, которая определяется путем вычисления критерия Стьюдента (t) по формуле:
t =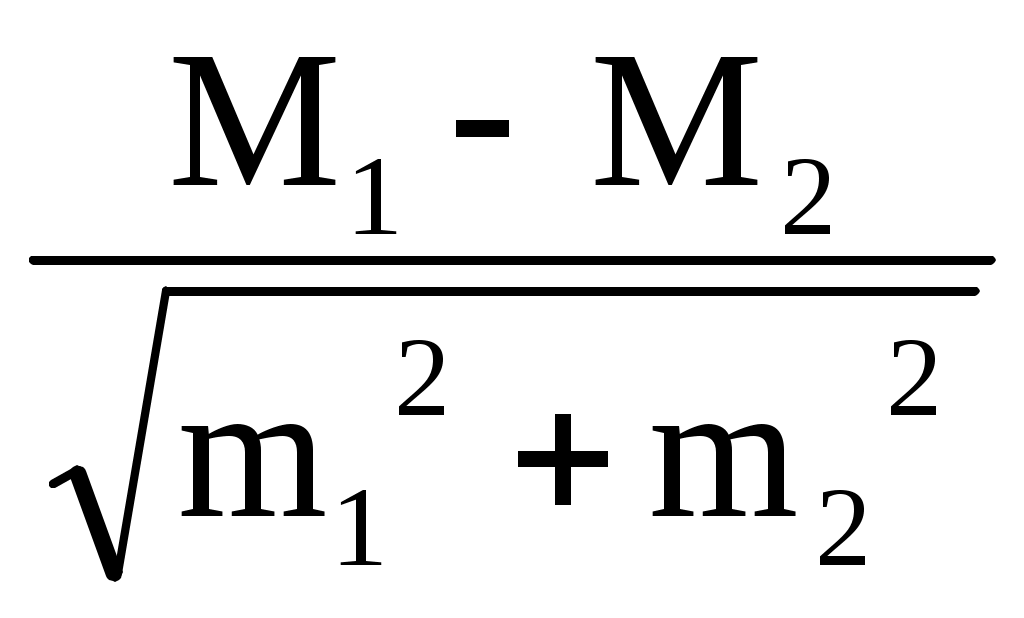
где: М₁ и М₂  средние арифметические взвешенные величины групп сравнения;

m₁ и m₂  ошибки средних арифметических взвешенных величин.

О ценка значений критерия (t) проводится таким образом: если t3, то отличия средних величин считаются достоверными (p<0,05), если t  3 — отличия средних величин считаются недостоверными (p>0,05).

Так если, например, в городах В. и К. проводится углубленный медицинский осмотр школьников 10 лет и полученные при этом показатели физического развития представляют:

- в городе В.: средняя длина тела мальчиков - 156,0 + 0,72 см, средняя масса тела - 44,40+0,38 кг,

- в городе К.: средняя длина тела мальчиков - 151,0 +0,58 см, средняя масса тела - 43,20+0,73 кг.

Оценка степени достоверности отличий показателей длины и массы тела школьников названных городов проводится:
Для длины тела: t = = = 5,6;

Для массы тела: t = = = 1,3.
Следовательно, в городе К. школьники 10 лет по длине тела существенно ниже, чем их ровесники из города В., что, естественно, нуждается в проведении дополнительного исследования направленного на изучение причин, влияющих на физическое развитие школьников.

В случае применения метода распределения относительных чисел вначале оценивают физическое развитие каждого ребенка отдельно, что входит в состав организованного коллектива и определяют оценочную группу, к которой она относится, а затем рассчитывают относительное число детей в каждой группе.

Достоверность отличий определяют по формуле:
t =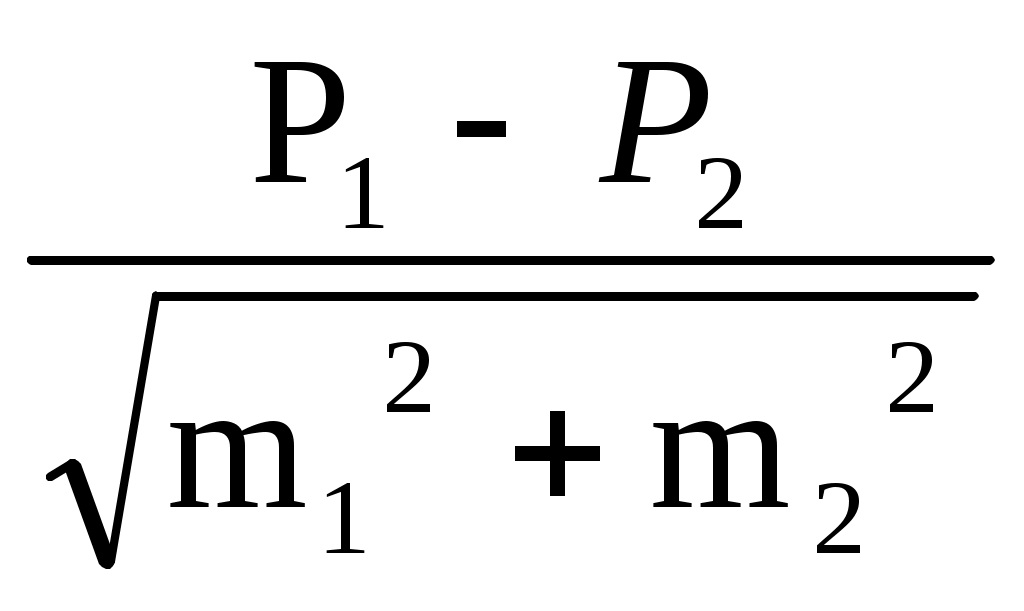
где: Р₁  количество детей (%) в первом коллективе, который оценивается;

Р₂  количество детей (%) во втором коллективе, который сравнивается;

m₁  ошибка Р₁;

m₂  ошибка Р_2.

Ошибку относительного количества детей определяют по формуле:
m₁ = ;
где: m₁  ошибка Р₁;

Р₁  количество детей (%) в первом коллективе, который сравнивается.

Метод сравнения средних квадратических отклонений используют для оценки однородности состояния здоровья и физического развития по определенным показателем. При этом считается, что чем больше значения стандартного отклонения (), тем большим будет размах колебаний исследуемого признака и, таким образом, степень ее неоднородности.

Корреляционный метод предоставляет возможность установить наличие определенной связи между ведущими характеристиками состояния здоровья и физического развития путем определения коэффициента корреляции (r). Если величина r равняется 0  корреляционной связи между исследуемыми признаками не существует. Вместе с тем, если величина r равняется 1  корреляционная связь между исследуемыми признаками является очень сильной. При значениях r в пределах от 0 до 0,3 корреляционную связь определяют как слабую, при значениях r в пределах от 0,3 до 0,5  как среднюю, при значениях r в пределах от 0,5 до 0,7  как сильную, при значениях r в пределах от 0,7 до 1,0  как очень сильную. В случае положительного значения r  связь следует определять как прямую (при увеличении одного исследуемого показателя другой возрастает), в случае отрицательного значения r  связь следует определять как обратную (при увеличении одного исследуемого показателя другой уменьшается).