открытый урок Алгбра 7. Формулы сокращённого умножения

• Название: Формулы сокращённого умножения
• Дата: 11.02.2023
• Размер: 49.47 Kb.
• Имя файла: открытый урок Алгбра 7.docx
• Тип: Урок; #930955

• 
  Открытый урок по алгебре.
  
• 
  Тема: "Формулы сокращённого умножения"
  
• 
  Козлова В.С,
  
• 
  Учитель математики МБОУ «СШ им.М. Горького»
  
• 
  Разделы: Математика
  
• 
  
  
• 
  Цель урока: научить учащихся применять формулы сокращенного умножения при выполнении упражнений  различной сложности  и творческих заданий.
  
• 
  Задачи урока:
  
• 
  Образовательная: 
  

• 
  Повторить знание формул сокращённого умножения;
  
• 
  Закрепить знание формул сокращённого умножения и их применение при упрощении выражений;
  
• 
  Отработка вычислительных навыков;
  
• 
  Формирование у учащихся мотивации к изучению предмета.
  

• 
  Развивающая:
  

• 
  Формировать умение анализировать,
  
• 
  Обобщать, развивать математическое мышление.
  
• 
  Формировать навыки самоконтроля, адекватной самооценки и саморегуляции деятельности.
  

• 
  Воспитательная:
  

• 
  Воспитание ответственности за выполненную  работу;
  
• 
  Воспитывать умение правильно оценивать результаты своего труда
  

• 
  Тип урока: урок обобщения и систематизации знаний.
  
• 
  Оборудование: демонстрационный материал, карточки с заданиями, раздаточный материал,  тесты в печатном виде, формулы сокращённого умножения.
  
• 
  Методы: словесный, репродуктивный, объяснительно-иллюстративный, проблемное изучение , практические, конструктивный или творческий.
  
• 
  Формы организации познавательной деятельности учащихся: фронтальный опрос, работа в парах, индивидуальная, коллективная, самостоятельная работа учащихся.
  
• 
  Технология реализации: дифференцированное обучение.
  
• 
  Структура урока:
  
• 
  1)Организационный момент.(1 мин)
  
• 
  2) Актуализация знаний. (10 мин)
  
• 
  3) Обобщение и систематизация знаний. (23 мин)
  
• 
  4) Контроль знаний. (6 мин)
  
• 
  5) Постановка домашнего задания. (2 мин)
  
• 
  6) Итог урока. (2 мин)
  
• 
  7) Рефлексия. (1 мин)
  
• 
  Ход урока
  
• 
  1. Организационный момент.
  
• 
  - Здравствуйте, ребята. Садитесь. На предыдущих уроках вы познакомились с формулами сокращенного умножения. Сегодня мы продолжим эту тему. Вы покажете, как вы знаете эти формулы, как умеете их применять. Запишите в тетрадях число и тему урока.
  Девиз урока: «Чему бы ты ни учился, ты учишься для себя».  (Петроний)
  
• 
  Прежде, чем приступить к работе, каждый из вас должен поставить перед собой цель сегодняшнего урока. Перед вами лежат оценочные листы, подпишите их, в левом столбце написаны цели, выберите те, которые соответствуют вашим, и поставьте напротив знак “+” или допишите свою. На каждом этапе урока вы будете оценивать себя, выставляя количество заработанных баллов  от 1 до 5 в оценочные листы.
  
• 
  Оценочный лист
  

“Я познание сделал своим ремеслом…”

• 
  Фамилия и имя:____________________________
  
• 
   
  
• 
  Задания
  
• 
  Баллы
  
• 
  1. Получить новые знания
  
• 
   
  
• 
  1. Тест – соответствие
  
• 
   
  
• 
  2. Показать свои знания
  
• 
   
  
• 
  2. Замени пропуски
  
• 
   
  
• 
  3. Получить хорошую оценку
  
• 
   
  
• 
  3. Игра “Алгебраическая мозаика”
  
• 
   
  
• 
  4.
  
• 
   
  
• 
  4. Применение формул
  
• 
   
  
• 
  5.
  
• 
   
  
• 
  5. Тест
  
• 
   
  
• 
   
  

 

• 
   
  
• 
   
  
• 
  усвоил полностью
  усвоил частично
  не усвоил
  
• 
  Продолжи одно из предложений:
  “Мне понятно…
  “Я запомнил…
  “Мне на уроке…
  “Я думаю…
  
• 
  
  
• 
  Сначала мы повторим пройденный материал.
  
• 
  2) Актуализация знаний.
  
• 
  Ребята, формулы сокращенного умножения имеют широкое применение в математике, особенно в старших классах. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений. Поэтому надо хорошо знать эти формулы и уметь применять их в преобразованиях выражений.
  
• 
  а) А сейчас мы начнем наш путь с повторения формул и правил. На доске записана левая честь формулы, нужно продолжить формулу, назвать её  и рассказать правило. (7 учеников)
  

а² – в² = (а – в)(а + в)
разность квадратов двух выражений

• 
  Разность квадратов двух выражений равна произведению их разности на их сумму.
  
• 
  (а + в)² = а² + 2ав + в²
  квадрат суммы двух выражений
  
• 
  Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе и плюс квадрат второго выражения.
  
• 
  (а  – в)² = а² – 2ав + в²
  квадрат разности двух выражений
  
• 
  Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе и плюс квадрат второго выражения.
  
• 
  (а + в)³ = а³ + 3а²в + 3ав² + в³
  куб суммы двух выражений
  
• 
  Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, плюс куб второго выражения.
  
• 
  (а – в)³ = а³ – 3а²в + 3ав² – в³
  куб разности  двух выражений
  
• 
  Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, минус куб второго выражения.
  
• 
  а³ + в³ = (а + в)(а2 – ав + в²)
  сумма кубов двух выражений
  
• 
  Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
  
• 
  а³ – в³ = (а – в)(а² + ав + в²)
  разность кубов двух выражений
  
• 
  Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
  
• 
  б) Найти  куб и квадрат выражений, найти произведение одночленов,  найти удвоенное произведение одночленов, найти утроенное произведение первого выражения на квадрат второго, найти утроенное произведение квадрата первого выражения на второе: (устный счет)
  

• 
  2a  и   3b; 
  
• 
  0,1b  и  0,2k;
  
• 
  m  и 1/4n;
  
• 
  x²2  и 2y²;
  
• 
  11ax  и 3by;
  
• 
  – 4b  и – 7a; 
  
• 
  2ab   и 5n; 
  
• 
  ab³  и    m³n4 .
  

• 
  3) Обобщение и систематизация знаний.
  
• 
  ЗАДАНИЕ №1:
  
• 
  Тест – соответствие (работа в парах).
  
• 
  Расшифровка. Для каждого выражения из левого столбца подберите ему тождественно равное в правом:  («5» - все верно,  «4» - 1- 2  ошибки, «3» - 3 ошибки)
  
• 
  формула
  
• 
  № ответа
  
• 
  ответ
  
• 
  буква
  
• 
  1
  
• 
  (x+3)²
  
• 
  1
  
• 
  4x²-9
  
• 
  О
  
• 
  2
  
• 
  x²-16
  
• 
  2
  
• 
  16x²-40xy+25y²
  
• 
  А
  
• 
  3
  
• 
  (2x-3)(2x+3)
  
• 
  3
  
• 
  (x-4)(x+4)
  
• 
  И
  
• 
  4
  
• 
  81-18x+x²
  
• 
  4
  
• 
  (3y+6x)²
  
• 
  Т
  
• 
  5
  
• 
  (4x-5y)²
  
• 
  5
  
• 
  x²+6x+9
  
• 
  Д
  
• 
  6
  
• 
  25x²-49y²
  
• 
  6
  
• 
  (9-x)²
  
• 
  Ф
  
• 
  7
  
• 
  9y²+36yx+36x²
  
• 
  7
  
• 
  (5x-7y)(5x+7y)
  
• 
  Н
  
• 
  Каждый ученик получает карточку, выполняет задание, получает соответствия:
  
• 
  1→5(Д), 2→3(И), 3→1(О), 4→6(Ф), 5→2(А), 6→7(Н), 7→4(Т).
  
• 
  Молодцы ребята, вы получили имя великого математика.  Показываю его портрет.
  
• 
  Историческая справка:  рассказ ученика. 
  
• 
  Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время,  все алгебраические утверждения выражали в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения.
  
• 
  ЗАДАНИЕ №2:
  
• 
  Замените одночленом так, чтобы получившееся равенство было тождеством. (Индивидуальное задание) Взаимопроверка. («5» - все верно,  «4» - 1- 2  ошибки, «3» - 3 ошибки)
  
• 
  Ответы: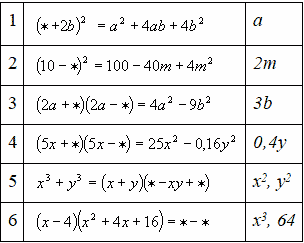
  
• 
  
  
• 
  - Какими формулами вы пользовались в данном задании?
  
• 
  ЗАДАНИЕ №3:  Игра “Алгебраическая мозаика”.
  
• 
  Составить из предложенных выражений формулы. Кто больше.
  
• 
  3х, 5у, 3х, 5у, 9х², 30ху, 27х³, 125х², 15ху, 25у² , 125у³.
  
• 
  Ответы: (Всего 7 формул.  («5» - все верно,  «4» - 1- 2  ошибки, «3» - 3 ошибки)
  

• 
  (3х + 5у)² = 3х²+30ху+25у²
  
• 
  (3х – 5у)(3х + 5у) = 9х²– 25у²
  
• 
  27х³ + 125у³ = (3х + 5у)(9х²+ 15ху+25у²)
  
• 
  (5у – 3х)² = 25у² – 30ху + 9х²
  

• 
  ЗАДАНИЕ №4:  Применение формул.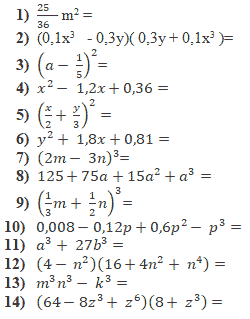
  
• 
  
  
• 
  4) Контроль знаний.  Следующий тест проверит ваше умение применять формулы сокращенного умножения при вычислении значений выражений и разложении на множители. Ваша цель – выбрать правильный ответ и записать нужную букву.
  
• 
  Учащиеся получают карточки с пятью заданиями. При правильных ответах из выбранных букв должно получиться слово «ВЕРНО».
  
• 
  Вариант 1:
  
• 
  1) Вычисли: 412 – 312
  
• 
  б) 72
  в) 720
  г) 730
  
• 
  2)Вычисли: 262  – 742
  
• 
  е) – 4800
  ж) 4800
  з) – 480
  
• 
  3) Разложи на множители: a⁴ – 8a² + 16
  
• 
  c) (a² + 4)²
  n) (a – 4)²
  p) (a² – 4)²
  
• 
  4) Разложи на множители: a⁶ – 8
  
• 
  н) (а² – 2) (а⁴ + 2а² + 4)
  к) (а³ – 4) (а³ + 4)
  л) (а²2 – 2) (а² + 2а + 4)
  
• 
  5) Разложи на множители: 25b² – 16c⁴
  
• 
  a) (5b – 4c²)²
  o) (5b – 4c²) (5b + 4с²)
  д) (5b – 4c) (5b + 4c)
  
• 
  Вариант 2:
  
• 
  1) Вычисли: 762 – 242
  
• 
  а) – 520
  в) 5200
  c) 52
  
• 
  2) Вычисли: 832 –732
  
• 
  e) 1560
  ж) 156
  з) 1540
  
• 
  3) Разложи на множители: 4 + 4b² + b⁴
  
• 
  к) (2 – b²)²
  п) (2 + b²)²
  р) (2 + b²)²
  
• 
  4) Разложи на множители: 1 – c⁹
  
• 
  н) (1 – c³) (1 + c³ + c⁶)
  м) (1 – c³) (1 + c³)      
  л) (1 – с³) (1 + 2с³ + с⁶)
  
• 
  5) Разложи на множители:  36x⁴ – 49y²
  
• 
  e) (6x² – 7y)²
  o) (6x² – 7y) (6x² + 7y)
  a) (6x – 7y) (6x + 7y)
  
• 
  Для проверки теста учащиеся показывают запись учителю и вместе с ним оценивают свою работу.
  
• 
  5) Постановка домашнего задания. Дифференцированная домашняя работа. Применив формулы сокращенного умножения, заполни таблицу: даны 5 пар выражений на «3» 3 любых пары, «4» - 4 пары, «5» заполнена вся таблица. Учить формулы и правила.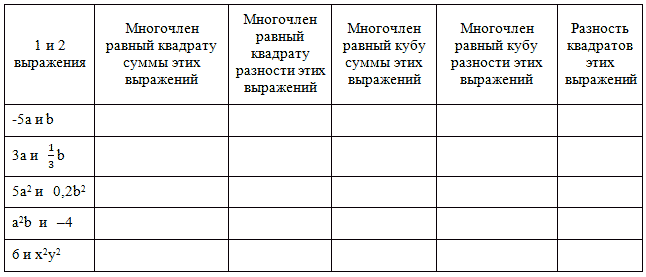
  
• 
  
  
• 
  6) Итог урока.
  
• 
  - Итак, ребята, урок подошел к концу.
  
• 
  Наук так много на земле,
  У всех – своя тематика.
  Но есть одна из них милей, 
  Зовётся математикой.
  В ней не бывает скользких мест,
  Всё строго в ней доказано,
  И с нею движется прогресс,
  И этим нам всё сказано.
  
• 
  -  Оценка ваша за урок будет в оценочном листе, который вы мне сейчас сдадите. Сложите все 5 оценок и разделите на 5, это и будет ваша оценка за урок. Ребята, достигли ли Вы своей цели на этом уроке? В оценочном листе подчеркните свой ответ.
  
• 
  7) Рефлексия. В оценочном листе продолжи одно из предложений:
  

• 
  “Мне понятно…
  
• 
  “Я запомнил…
  
• 
  “Мне на уроке…
  
• 
  “Я думаю…
  

• 
  - Урок закончен. До свидания!