Инстэк_коллоквиум_шпора. Функциональный спрос. Характеристики товаров и выбор потребителя (подход Ланкастера)
 Скачать 1.18 Mb. Скачать 1.18 Mb.
|
Функциональный спрос. Характеристики товаров и выбор потребителя (подход Ланкастера). Функциональным спросом является спрос на блага, который определяется исключительно потребительскими свойствами, присущими экономическому благу (товару или услуге). Функциональный спрос зависит от максимизации функции полезности потребителя, он убывает или возрастает в зависимости от качеств этого блага с точки зрения потребителя, качеств, которые повышают полезность потребителя". Ограниченность классической модели потребительского поведения заключается в том, что она базируется на субъективной информации. Предпочтения по отношению к различным товарам (даже если товары идентичны) субъективны; объективная информация ограничивается такими показателями, как цена и доход. Задача этого параграфа — исследовать проблему потребления на основе более объективных параметров. Новый подход к потребительской теории был впервые предложен Кельвином Ланкастером. Подход Ланкастера основан на трех предпосылках ● всем благам присущи измеряемые характеристики, или атрибуты; ● атрибуты могут быть измерены объективными параметрами; ● полезность блага, основанная на атрибутах, объективно измерима. Например, два главных атрибута (характеристики), протеин (Z t ) и жир (Z 2), содержатся в мясе и в его заменителях. Если бы это были единственные атрибуты, которые имеют существенное значение для потребителя, то функция полезности имела бы вид; U = U (Z ,, Z 2). Функция полезности остается субъективной (разные люди имеют различные предпочтения относительно жира и протеина), но теперь к объективным характеристикам «цена» и «доход» добавляются не менее объективные «жир» и «протеин». На рисунке каждый вид продукта классифицирован по параметрам: «жир-протеин» в соответствии с удельным весом каждого из двух компонентов в товаре. 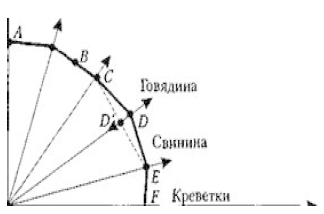 Относительные количества жира и протеина представлены с помощью наклонов «атрибутивных лучей», исходящих из осей координат. В данном случае пшеница и креветки являются двумя крайними случаями сочетаний протеина и жиров. Содержание жира увеличивается при переходе от пшеницы к рыбе, птице и т. п. Цены и доход определяют достижимую величину сочетаний жира и протеина и формируют границу характеристик: ABCDEF. Граница характеристик (characteristic frontier): положение потребительского максимума продуктовых характеристик, которые определяются доходом потребителя, рыночными ценами и набором атрибутов, содержащихся в товарах. Угол атрибутивного луча указывает удельный вес протеина и жира и объем данного блага, который может получить потребитель, если он потратит весь свой продуктовый бюджет на его покупку. К примеру, предположим, что 1 кг рыбы содержит 10 ед. протеина и 1 ед. жира. Если продуктовый бюджет потребителя составляет 100 р. в неделю, а цена рыбы 2,5 р. за килограмм, то потребитель может купить максимально 40 кг рыбы в неделю, что соответствует 400 ед. протеина и 40 ед. жира. Это определяет положение точки В на рисунке. Положение прочих точек (С, D , Е, F) определяется аналогично. Функциональный и нефункциональный спрос. Функциональный спрос — спрос, обусловленный присущими данному благу потребительскими качествами. Нефункциональный спрос — спрос, возникающий у потребителя не в силу потребительских характеристик товара, а под влиянием каких-либо других факторов. Нефункциональный спрос в свою очередь делится на три неравные группы: ● Спрос, обусловленный внешними (экзогенными) воздействиями на полезность товара. Здесь выделяют: ○ эффект присоединения к большинству ○ эффект сноба ○ эффект показательного потребления ● Спекулятивный спрос ● Нерациональный спрос Наиболее значительная часть нефункционального спроса обусловлена экзогенными воздействиями на полезность. Это означает, что полезность товара для потребителя увеличивается или уменьшается в зависимости от того, покупают ли этот товар другие люди, либо вследствие того, что этот товар имеет более высокую цену по сравнению с другими товарами. Эффект присоединения к большинству. Под эффектом присоединения к большинству понимается та величина, на которую возрастает индивидуальный спрос на товар вследствие того, что расширяется рыночный спрос на него, или другими словами, из-за того, что другие люди также покупают этот самый товар. Эффект отражает стремление людей не отставать от жизни, от моды, соответствовать тому социальному кругу, в котором они хотели бы вращаться. Чем больше смещается кривая индивидуального спроса (d) под воздействием увеличения рыночного спроса (D), тем выше данный эффект. 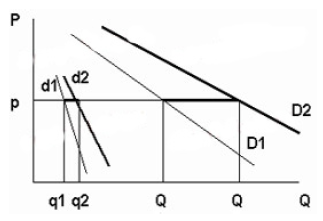 Эффект сноба. Эффект сноба характеризуется величиной, на которую сократится индивидуальный спрос вследствие того, что другие тоже потребляют данный товар, т.е. вследствие увеличения рыночного спроса. Этот эффект выражает стремление людей к исключительности, стремление отличаться друг от друга, выделяться из толпы. Падение спроса тем больше, чем большим спросом данный товар пользуется у других покупателей. 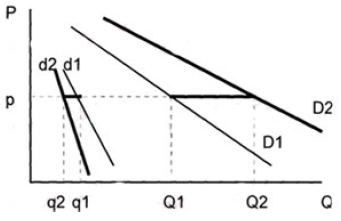 И эффект присоединения к большинству и эффект сноба могут быть количественно оценены через коэффициент количественной эластичности, показывающий степень количественного изменения индивидуального спроса при изменении рыночного спроса на 1%. Коэффициент подсчитывается по формуле: 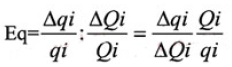 qi — величина индивидуального спроса на товар i; Qi — величина рыночного спроса на товар i; Если Eq > 0, то имеет место эффект присоединения к большинству Если Eq < 0, то наблюдается эффект сноба. Абсолютное значение данного коэффициента характеризует величину рассматриваемых эффектов. Эффект Веблена. Эффект показательного потребления, или эффект Веблена отражает такое на первый взгляд парадоксальное явление, как увеличение спроса на некоторый товар в силу того, что он имеет более высокую по сравнению со своими аналогами цену. Эффект Веблена характеризует величину, на которую возрастает индивидуальный спрос вследствие увеличения цены на рассматриваемый товар. Эффект наблюдается в том случае, когда потребитель ассоциирует повышенную цену с большей престижностью, что и вызывает дополнительный спрос. 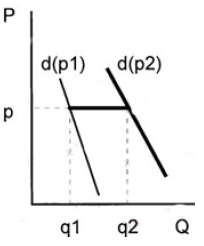 Обратная зависимость между ценой и величиной спроса сохраняется, но сама кривая спроса сдвигается под воздействием эффекта вправо, поскольку в глазах потребителя один и тот же товар с низкой ценой (P1 непрестижный) и с высокой ценой (P2 престижный) являются различными товарами с различными кривыми спроса соответственно d(P1) и d(P2). Количественное значение эффекта Веблена может быть оценено через ценовую эластичность спроса, характеризующую степень изменения спроса при изменении цены на 1%. Коэффициент ценовой эластичности спроса подсчитывается по уже известной нам формуле: 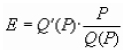 Q(P) — функция спроса по цене P — рыночная цена Если эффект Веблена отсутствует, и товар не принадлежит к группе товаров Гиффена, то коэффициент ценовой эластичности является отрицательным, E<0. Положительное значение коэффициента, E>0, может говорить о существовании эффекта показательного потребления тем более значимого, чем выше абсолютное значение данного коэффициента.
Выбор в условиях неопределенности. Факторы, обусловливающие необходимость учета фактора неопределенности многообразны. ● Характеристики некоторых товаров, приобретаемых потребителем, изначально не могут быть точно определены в момент покупки. Например, это касается рискованности и доходности ценных бумаг, выпускаемых компаниями. ● К неопределенности приводит действие внешних факторов (states of the World, state of Nature ) влияющих на выбор, осуществляемый индивидом, но никак от него не зависящих. Например, это может касаться регулятивных, правовых, коньюнктурных и пр. изменений, непосредственно затрагивающих деятельность компании и интересы акционеров. ● Неопределенность может порождаться непредсказуемым поведением контрагентов, например, благосостояние инвесторов в существенной степени зависит от того, насколько эффективным будет руководство компанией, осуществляемое менеджерами, от того окажется политика, проводимая Советом директоров компании и в какой в какой степени, она сможет препятствовать возможным злоупотреблениям со стороны высших менеджеров и пр. Санкт – Петербургский парадокс. Собственно привлекательность лотереи или игры можно попытаться оценить, определив уровень ее среднего выигрыша Е(W) = Однако еще в 18 веке такого рода подход начал вызывать серьезные возражения. В частности, Николас Бернулли в 1728 году обратил внимание на то, что ни один игрок не будет готов заплатить сколь-нибудь заметную сумму за участие в игре, математическое ожидание выигрыша в которой равно бесконечности. Суть рассмотренной им игры состояла в следующем: бросается монета, и в том случае, если орел выпадает в i - ом бросании, игрок получает выигрыш, равный 2^i. Вероятность выпадения орла в i - ом бросании составляет рi=(1/2)i, т.е.1/2, 1/4 и т.д.
Е(W) = Парадоксальность этой ситуации состоит в том, что не найдется желающих платить, скажем 1 млн долл, за право участия в подобной игре, несмотря на то, что эта сумма несопоставимо меньше математического ожидания выигрыша - бесконечности. Собственно, одновременно выдвинутая Габриэлем Крамером и Даниэлем Бернулли гипотеза о том, что важна не сама сумма выигрыша, а та полезность которую получает потребитель1 , не является решением этого так называемого Санкт-Петербургского парадокса , но она способствовала весьма здравому теоретическому переосмыслению проблемы. Привычные аксиомы потребительского выбора, лишь несколько модифицированные применительно к рассматриваемым ситуациям неопределенности. Мы будем полагать, что предпочтения индивида на пространстве простых лотерей L асимметричны и негативно транзитивны. Во многом мы повторим традиционные аксиомы анализа поведения потребителя, когда будем говорить о том, что - объекты выбора (в данном случае лотереи) должны быть четко определены; -ситуации с одними и теми же исходами должны вести к одинаковым решениям; - индивид должен быть в состоянии произвести анализ имеющихся альтернатив; -предпочтения относительно лотерей должны быть транзитивны, локально ненасыщаемы и т.д. Особое положение в перечне исходных аксиом занимает аксиома непрерывности предпочтений индивида относительно простых лотерей. Содержательно эта предпосылка важна с той же самой точки зрения, что и в условиях определенности она позволяет упростить анализ, отказавшись от рассмотрения поведения индивидов, обладающих лексикографическими предпочтениями. Например, покупка акций, облигаций или прочих товаров, чья покупка сопряжена с той или иной степенью неопределенности, сопровождается постоянным торгом между повышением надежностью компании и понижением уровня доходности ценных бумаг. Для индивида с лексикографическими предпочтениями и приоритетом безопасности вложений над экономической выгодой такого рода решение было бы невозможно. Теория ожидаемой полезности Неймана-Моргенштерна и результаты ее тестирования. Теория основывается на аксиомах: Аксиома сравнимости (полноты). Для всего множества S неопределенных альтернатив (возможных исходов) индивид может сказать, что либо исход х предпочтительнее исхода у (х > у), либо у > х, либо индивид безразличен в отношении к выбору между х и у (х = у). Аксиома транзитивности (состоятельности). Если х > у и у > z, то х > z. Если х = у и у = z, то х = z. Аксиома измеримости. Если х > у = z или х = у > z, то существует единственная вероятность α, такая, что у = G(x, z: α). Аксиома ранжирования. Если альтернативы у и и находятся по предпочтительности между альтернативами х и z и можно построить игры, такие, что индивид безразличен в отношении к выбору между у и G(x, z: α1), a также к выбору между и и G(x, z: α2), то при α1 > α2, у > и. При названных предположениях американскими учеными Нейманом и Моргенштерном было показано, что лицо принимающее решение (ЛПР) при принятии решения будет стремиться к максимизации ожидаемой полезности. Другими словами, из всех возможных решений он выберет то, которое обеспечивает наибольшую ожидаемую полезность. Сформулируем определение полезности по Нейману-Моргенштерну. Полезность – это некоторое число, приписываемое лицом, принимающим решение, каждому возможному исходу. Функция полезности Неймана-Моргенштерна для ЛПР показывает полезность, которую он приписывает каждому возможному исходу. У каждого ЛПР своя функция полезности, которая показывает его предпочтение к тем или иным исходам в зависимости от его отношения к риску. Ожидаемая полезность события равна сумме произведений вероятностей исходов на значения полезностей этих исходов. Проиллюстрируем практическую реализацию введенных понятий на примере расчета ожидаемой денежной оценки (ОДО) и сопоставления этого значения с полезностью. Для принятия решения в случае небезразличия ЛПР к риску необходимо уметь оценивать значения полезности каждого из допустимых исходов. Дж. Нейман и О. Моргенштерн предложили процедуру построения индивидуальной функции полезности, которая (процедура) заключается в следующем: ЛПР отвечает на ряд вопросов, обнаруживая при этом свои индивидуальные предпочтения, учитывающие его отношение к риску. Значения полезностей могут быть найдены за два шага. Шаг 1. Присваиваются произвольные значения полезностей выигрышам для худшего и лучшего исходов, причем первой величине (худший исход) ставится в соответствие меньшее число. Шaг 2. Игроку предлагается на выбор: получить некоторую гарантированную денежную сумму V, находящуюся между лучшим и худшим значениями S и s, либо принять участие в игре, т.е. получить с вероятностью р наибольшую денежную сумму S и с вероятностью (1 – р) – наименьшую сумму s. При этом вероятность следует изменять (понижать или повышать) до тех пор, пока ЛПР станет безразличным в отношении к выбору между получением гарантированной суммы и игрой. Пусть указанное значение вероятности равно р0. Тогда полезность гарантированной суммы определяется как среднее значение (математическое ожидание) полезностей наименьшей и наибольшей сумм, т.е. U(V) = p0 U(S) + (1 – p0)U(s). (12.1) Таким образом, если определена шкала измерения, то может быть построена функция полезности ЛПР. Парадокс Алле. Парадокс демонстрирует неприменимость теории максимизации ожидаемой полезности в реальных условиях риска и неопределённости. Автор корректно, с позиций математики, объясняет суть парадокса. Парадокс демонстрирует, что реальный агент, ведущий себя рационально, предпочитает не поведение получения максимальной ожидаемой полезности, а поведение достижения абсолютной надежности. Сам Алле провёл психологический эксперимент, описанный ниже, и получил парадоксальные результаты. Индивидам предлагают выбор по одному решению из двух пар рискованных решений. В первом случае в ситуации A есть 100 % уверенность в получении выигрыша в 1 млн франков, а в ситуации B имеется 10 % вероятность выигрыша в 5 млн франков, 89 % — в 1 млн франков и 1 % — не выиграть ничего. Во втором случае тем же индивидам предлагается сделать выбор между ситуацией C и D. В ситуации C имеется 10 % вероятности выигрыша в 5 млн франков и 90 % не выиграть ничего, а в ситуации D 11 % составляет вероятность выигрыша в 1 млн франков и 89 % — не выиграть ничего. Алле установил, что значительное большинство индивидов в этих условиях предпочтет выбор ситуации A в первой паре и ситуации C во второй. Этот результат воспринимался как парадоксальный. В рамках существовавшей гипотезы индивид, отдавший предпочтение выбору А в первой паре, должен выбрать ситуацию Д во второй паре, а остановивший выбор на В должен во второй паре отдать предпочтение выбору С. Алле математически точно объяснил этот парадокс. Его основной вывод гласил, что рационально действующий агент предпочитает абсолютную надежность. Парадокс можно сформулировать в виде выбора между двумя вариантами, в каждом из которых с некоторой вероятностью достаётся та или иная сумма денег: 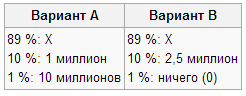 Здесь X — неизвестная выбирающему сумма. Какой выбор будет более разумным? Результат останется прежним, если «неизвестная сумма» X — это 100 миллионов? Если это «ничего»? Математическое ожидание в первом варианте равно а во втором: поэтому математически второй вариант B выгоднее независимо от значения X. Но люди боятся нулевого исхода в варианте B и поэтому чаще выбирают A. Однако если |
