Инстэк_коллоквиум_шпора. Функциональный спрос. Характеристики товаров и выбор потребителя (подход Ланкастера)

• Название: Функциональный спрос. Характеристики товаров и выбор потребителя (подход Ланкастера)
• Анкор: Инстэк_коллоквиум_шпора.doc
• Дата: 01.02.2017
• Размер: 1.18 Mb.
• Имя файла: Инстэк_коллоквиум_шпора.doc
• Тип: Документы; #1560
• страница: 2 из 4

Теоретические концепции поведения экономических агентов в условиях неопределенности и их тестирование. «Рамочные» эффекты.

Принимая решение в условиях неопределенности, индивид всегда участвует в своего рода лотерее. Например, покупая некую акцию, инвестор может как получить значительный выигрыш, так и лишиться инвестированных средств Обозначив через x_i исходы в такого рода лотерее, мы можем записать эту лотерею следующим образом

L₁ р о х₁ (1 - р) о х₂,

что означает: "Индивид с вероятностью р получит приз х₁и с вероятностью (1 - р) - приз х₂" Альтернативой участию в этой лотерее может быть покупка иной акции

L₂ q о х₃ (1 - q) о х₄

Какую из этих двух лотерей предпочтет индивид? При совпадении перечня исходов(призов) в обеих лотереях (х₁= х₃; х₂= х₄ ) ответ на этот вопрос может быть обусловлен вероятностным распределением выигрышей. Изменив вероятности получения призов в сторону увеличения вероятности получения лучшего приза, мы получим новую лотерею, которая будет стохастически доминировать исходную (более подробно о стохастическом доминировании будет сказано позднее). Но это отнюдь не снимает проблему ранжирования лотерей при отсутствии четко выраженного стохастического доминирования, столь частого при большем количестве возможных исходов.

Лотереи. Сведение сложных лотерей к простым.

Простая лотерея может быть описана как вектор вероятностей выпадения возможных исходов: L(р)=(р₁, р₂ , ... , р_n), где _i p _i =1 и p _i ≥ 0 для всех i =1, ... , n.

Геометрически простая лотерея соответствует точке на (n -1)-мерном симплексе 

Рис.1.1. n = 2



Рис.1.2. n = 3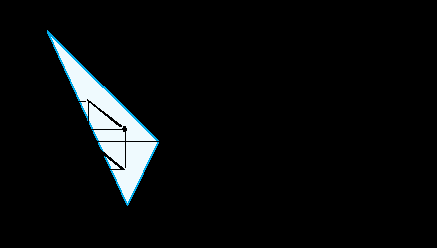



Сложные лотерии (compound lotteries)- в отличие от простых лотерей - допускают возможность рассмотрения в качестве возможных исходов не только получение индивидом неких конкретных "призов", но так называемых "вторичных" лотерей. Сложной, например, является лотерея, включающая в перечень возможных призов билеты следующего тура этой лотереи.

Математически сведение сложной лотереи к простой, т.е. определение вероятностей получения конечных призов, может быть осуществлено путем расчета сумм условных вероятностей, т.е. вероятностей получения этих призов во вторичных лотереях, взвешенных по вероятностям выпадения вторичных лотерей:

p(x_i) = _i p(x_iL_j ) p( L_j).

Например, если призами в первичной лотерее выступают лотереи

L₁=(0.6, 0.4) и L₂=(0.2, 0.8), причем вероятность выигрыша L₁равна 2/3, а вероятность выигрыша L₂равна соответственно 1/3, то такая сложная лотерея будет эквивалентна простой лотерее с вероятностями получения конечных призов

(0.6 ^х (2/3) + 0.2 ^х (1/3), 0.4 ^х (2/3) + 0.8 ^х (1/3) ) = (14/30, 16/30).

Графически этот процесс сведения этой сложной лотереи к простой представлен на рис. 1.3.а, а следующий рисунок 1.3.б иллюстрирует сходную процедуру в предположении существования ( в каждой из двух вторичных лотерей ) уже не двух, а трех конечных призов.

1.3.а

1.3.б

Допустимость подобного сведения сложных лотерей к простым следует оговорить как отдельную предпосылку дальнейшего анализа (RCLA - the reduction of compound lotteries axiom), ибо с точки зрения отдельного индивида различные сложные лотереи, сводимые к одной и той же простой лотерее, могут оцениваться весьма различным образом. В частности, Джошуа Ронен (Ronen,1973) убедился, что даже простая перестановка двух этапов лотереи влияет на ее привлекательность для индивидов,а именно, семидесятипроцентный шанс получить 100 долл с вероятностью 30 % оказался более привлекательным для опрашиваемых, чем тридцатипроцентный шанс получить 100 долл с вероятностью 70 %. Но подобного рода соображения мы пока оставим в стороне, и в дальнейшем будем полагать эквивалентными различные сложные лотереи, сводимые к одной и той же простой лотерее.

Стохастическое доминирование.

Стохастическое доминирование 1-ого рода:

Если распределение F первично стохастически доминирует распределение G, то при распределении выигрышей F мат. ожидание выигрыша будет больше, чем при распределении G и ожидаемая полезность будет больше( Eu(F) > Eu(G) )
Стохастическое доминирование 2-ого рода:

Распределение F вторично стохастически доминирует распределение G, если при одинаковом мат. ожидании дисперсия выигрышей G больше.
Стохастическое доминирование первого рода.

Рассмотрим два распределения F(W) и G(W)(см. рис(2.1.а).

С одной стороны, с некоей заданной вероятностью можно получить выигрыш

W ≤ wF - при распределении F и W ≤ wG - при распределении G . Т.к. F(W ) ≤ G(W ) для любого W, то, следовательно, wF > wG , что позволяет оценивать распределение F как менее рискованное. Иначе, более корректно, эту мысль можно сформулировать, указав на стохастическое доминирование распределения F распределения G.
Def. Распределение F(W) первично стохастически доминирует распределение G(W) (F(W) first-order stochastically dominates G(W)), тогда и только тогда, когда F(W ) ≤ G(W) для любого W.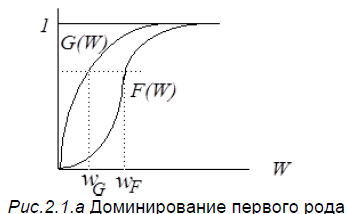



Соответственно, если распределение F первично стохастически доминирует

распределение G, то
• при распределении выигрышей F математическое ожидание выигрыша

будет выше чем при распределении G:



Графически это может интерпретироваться следующим образом(простоты ради зададим в данном случае совпадающие интервалы выигрышей):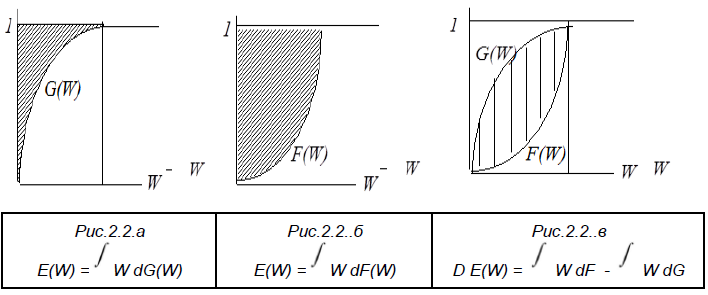



• при распределении выигрышей F ожидаемая полезность будет выше, чем при распределении G, т.е. для любой неубывающей функции u(W) выполняется условие



Несмотря на то, что стохастическое доминирование первого рода позволяет нам проранжировать лотереи как по уровню математического ожидания выигрыша, так и по уровню их ожидаемой полезности, обратное неверно, т.е. ни по уровню математического ожидания выигрыша , ни по уровню ожидаемой полезности нельзя делать вывод о стохастическом доминировании первого рода, поскольку ранжирование лотерей с точки зрения доминирования первого рода является частичным. Например, распределение G(W ) первично стохастически доминируется распределениями F(W) и F '(W), но не существует возможности,

рассматривая лишь доминирование первого рода, проранжировать эти два последние распределения.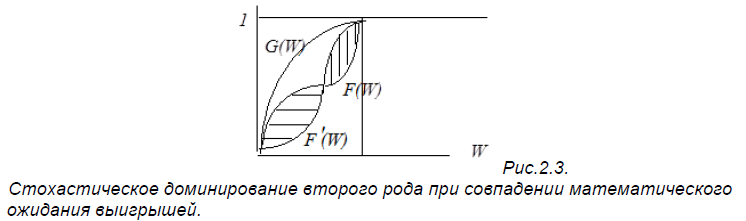



Несколько упрощая рассмотрение стохастического доминирования второго рода, сконцентрируемся лишь на тех распределениях, которые характеризуются совпадением математических ожиданий выигрышей.
Итак, две игры могут иметь одно и тоже математическое ожидание выигрыша, но различаться в степени своей рискованности. Например, игра, в которой с вероятностью 1/2 можно выиграть и с вероятностью 1/2 проиграть h долларов всегда будет менее рискованной чем игра, где с равными вероятностями можно выиграть или проиграть 2 h долларов. В подобном случае уместно говорить о стохастическом доминировании второго

рода или вторичном стохастическом доминировании.
Def. Распределение F(W) вторично стохастически доминирует

распределение G(W) ( F(W) second-order stochastically dominates G (W) ),

имеющее такое же математическое ожидание



если распределение G предполагает больший разброс выигрышей, т.е. его

дисперсия больше.
Пример. Сравним две игры, имеющие распределение G(W) и F(W) .В первой игре с вероятностями 0.25 можно выиграть 1, 2, 3 и 4. Во второй с вероятностями 0.5 можно получить 2 и 3. В обоих случаях математическое ожидание одинаково - 2.5 , что графически иллюстрируется совпадением площадей заштрихованных фигур.
Но поскольку в распределении G(W) задан больший разброс выигрышей, т.е. его дисперсия выше, чем при распределении F(W), оно является более рискованным.



Без доказательства приведем теорему, гласящую, что, если распределение F(W)вторично стохастически доминирует распределение G(W), то для любой возрастающей вогнутой функции полезности u(W) выполняется условие


Достоверный эквивалент лотереи, рисковая премия, рисковая

нагрузка, вероятностная премия.

Достоверным эквивалентом лотереи l называется величина l^ такая, что f(l^)=Ml[f] (полезность l^ равна ожидаемой полезности l). Т.е. для ЛПР безразлично, получить l^ наверняка или участвовать в лотерее l. Достоверный эквивалент единственен, т.к. f монотонная.
Рисковая премия (risk premium), обозначаемая в дальнейшем r, представляет собой максимальную плату, которую не склонный к риску индивид готов заплатить за то, чтобы избавиться от предстоящей ему справедливой игры, и , соответственно, равна разности между математическим ожиданием выигрыша E(W) и величиной достоверного

эквивалента игры (c):
Рисковая премия - часть страховой премии, которая расходуется страховщиком на создание необходимого фонда оплаты сумм страхового возмещения. Премия за риск неполучения доходов, предусмотренных основным сценарием проекта, определяется из условия равенства между

ожидаемым эффектом проекта, рассчитанным при безрисковой норме дисконта, и эффектом основного сценария, рассчитанным при норме дисконта, включающей поправку на риск. Разность между ожидаемым выигрышем и ценой продавца(достоверным эквивалентом лотереи) - премия

за риск.

Нагрузка (рисковая??) - часть страхового тарифа, предназначенная для покрытия затрат на проведение страхования и создания резерва (фонда) предупредительных мероприятий. В составе нагрузки может быть предусмотрена прибыль от проведения страховых операций.
Рисковая нагрузка - Можно добиться безразличия не склонного к риску индивида между гарантированным обладанием W0 и рискованными инвестициями, имеющими такое же математическое ожидание выигрыша, предложив ему денежную компенсацию l = W* - W0 за принятие этой справедливой игры. При этом вполне логичным представляется интерпретация подобной величины рискового вознаграждения или

рисковой нагрузки( в англоязычной литературе называемой risk loading) как готовности индивида принимать компенсацию (WTA) или же компенсирующей вариации дохода, подобно тому как рисковая премия r т.е.плата, которую индивид готов заплатить за то, чтобы избежать уготованной ему справедливой игры, интерпретировалась нами как

эквивалентная вариация дохода или готовность платить(WTР).
При фиксации уровня выигрышей, повышение математического ожидания выигрыша может быть достигнуто за счет приращения вероятности получения лучшего приза. Подобное приращение вероятности , делающее не склонного к риску индивида безразличным между участием и неучастием в игре: получило название вероятностной премии.
Мера абсолютной несклонности к риску Арроу-Пратта. САRА- Функции.

Меры Эрроу—Пратта (Arrow-Pratt measures) — количественные меры неприятия риска.
Абсолютная м. Э.-П. — скорость убывания предельной полезности богатства; относительная м.
Э.-П. — эластичность полезности по богатству, взятая с обратным зна-ком.

Для обоснования показателя степени неприятия риска индивидуумом используются меры Эрроу-Пратта – относительная и абсолютная. Абсолютная мера степени неприятия риска имеет вид: APa(I)=-u”(I)/u’(I).
Эти меры выражают свойства предпочтений индивидуума, а не только

описывающих их функций полезности.
Эта наиболее часто используемая мера несклонности к риску, названная по именам экономистов, независимо друг от друга разработавших ее в 1960-х годах, представляет собой дробь в числителе которой стоит вторая, а в знаменателе - первая производная функции полезности, взятую с обратным знаком. Знак "минус" добавляется с тем, что этот показатель несклонности индивида к риску был тем больше, чем менее индивид к нему склонен, т.е. был возрастающим по степени несклонности к риску.
risk-averse APa(I) > 0

risk-lover APa(I) < 0

risk-neutral APa(I) = 0
Выбор именно отношения - u "(I)/ u '(I) в качестве меры абсолютной

несклонности к риску был обусловлен, в первую очередь, тем обстоятельством, что для игр с незначительными выигрышами оно пропорционально тому количеству денег, которое в справедливой игре не склонный к риску индивид готов максимально заплатить

за страховку, т.е. величине рисковой премии.
CARA: функции полезности CARA описывают предпочтения

индивида с постоянной абсолютной несклонностью к риску.
R_A = - u ''(W)/ u '(W) = const u ''(W)/ u '(W) = - R_A
Для того, чтобы вывести вид функций полезности, характеризуемых этим свойством, решим соответствующее дифференциальное уравнение или же просто проинтегрируем это уравнение дважды. Результат первого интегрирования:

l n u '(W)= C₁ - R_AW u '(W)= exp (C₁ - R_AW), где C₁ - константа интегрирования
Результат второго интегрирования:

u (W) = C₂ - R_A^-1 еxp ( k₁ - R_A W)
Обозначим а = C₂ ; _{b =} R_A^-1еxp C₁ .
Итак, функции полезности u (W)= а - b еxp ( - R_A W) описывают предпочтения индивида с постоянной абсолютной несклонностью к риску.

Поскольку эта кардиналистская функция полезности единственна с точностью до аффинного преобразования, константы могут быть опущены, и тогда u (W)= - еxp ( - R_AW) .
Обмен в условиях неопределенности.

а) риски L индивидуальные и негативно коррелированные

Воспользуемся диаграммой Эджворта для анализа взаимодействия, возникающего между индивидами, столкнувшимися с независимыми негативно коррелированными рисками. Негативная коррелированность рисков означает, что в состоянии 2 потери терпит индивид 1, в то время как в состоянии 1 - индивид 2.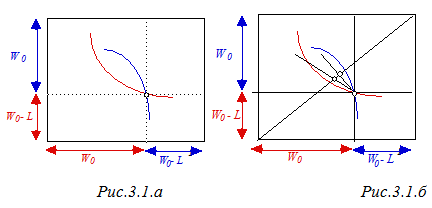



Обмен между индивидами взаимными обязательствами на случай наступления того или иного состояния(state--contigent claims to wealth) имеет смысл только до того момента, когда станет ясно, какое из двух возможных состояний реализовалось. Простоты ради будем полагать, что оба индивида первоначально располагают одинаковой суммой денег W₀ , и подвергаются одинаковому риску понести потери L . Подобные условия обусловливают равенство сторон диаграммы Эджворта (длина стороны квадрата равна 2 W₀ - L).

То, что диаграмма Эджворта имеет квадратный вид, предполагает отсутствие общественных или системных рисков (уровень суммарного богатства в различных состояниях не варьируется). Если же говорить о рисках индивидуальных, то стремясь застраховать себя от них, индивиды могут заключить договор, в соответствии с которым "счастливчик" всякий раз делится с "неудачником" некоторой частью своего богатства.
При независимости функций полезности Бернулли от выпавшего состояния мира и совпадении оценок вероятности выпадения различных состояний, контрактная кривая будет представлять собой диагональ квадрата, совпадая с линиями уверенности агентов. Действительно, на линии уверенности w₁ = w₂, а, соответственно,


что обеспечивает совпадение предельных норм замещения с отношением вероятностей, а, следовательно, и друг с другом :

Это делает не просто возможным, но и оптимальным - предоставление всем индивидам полной страховки. Строго говоря, размеры платежей могут быть различными - все зависит от того, насколько сильны позиции каждой из сторон в ходе торга(т.е. то, что по английски называется a bargaining power - Рис.3.1.б).
В частности, при равном влиянии участников возможно заключение "справедливого" контракта, предполагающего изъятие у каждого из них денежной суммы, равной справедливой премии (сдвиг влево вверх вдоль линии постоянного ожидаемого выигрыша вплоть до точки на кривой уверенности). Подобное распределение предполагает, что первый индивид в любом из выпавших состояний получает сумму, равную математическому ожиданию выигрыша, т.е. W₀ - L, где - вероятность выпадения второго, неблагоприятного для него "состояния мира", а второй - W₀- (1-)) L. Например, при = 1/3 первый индивид в благоприятном для него первом состоянии заплатит второму индивиду L/3, но во втором состоянии получит компенсацию, равную (2 L/3). В результате он будет полностью застрахован, получая в любом из возможных состояний сумму, равную математическому ожиданию его выигрыша, т.е. W₀- (L/3). Полная страховка будет обеспечена и второму индивиду, но уровень его богатства в обоих состояниях будет ниже(ввиду более высокой вероятности того, что именно он понесет потери) и равенW₀- (2 L/3).
Как бы то ни было, объединение риска в условиях, когда его осуществляют два не склонных к риску индивида с идентичными, но негативно коррелированными распределениями выигрышей, позволяет им обоим повысить уровень получаемой полезности.
б) риски индивидуальные - равные, но некоррелированные (независимые).

Описанное выше объединение рисков имеет смысл и в случае независимых распределений выигрышей индивидов. Как и прежде, полагая равенство сумм W₀, которыми первоначально располагают индивиды, и совпадение размеров возможных потерь L, предположим, что оба индивида сталкиваются с одинаковой вероятностью понести эти потери и для каждого из них она равна .
В результате возможно выпадение одного из четырех состояний:

	Состояние	Вероят-ность	индивид 1	индивид 2	Суммарное богатство	Богатство в расчете на одного индивида
1	никто не теряет	(1 -)2	W0	W0	2W0	W0
2	все теряют	2	W0 - L	W0 - L	2(W0 - L)	W0 - L
3	теряет первый	(1-)	W0 - L	W0	2W0 - L	(2W0 - L)/2
4	теряет второй	(1-)	W0	W0 - L	2W0 - L	(2W0 - L)/2

Ожидаемая полезность каждого индивида взятого в отдельности, т.е.

Еu(1) = u(W₀ - L) + (1-)u(W₀)

может быть увеличена, в частности, если индивиды объединят свои риски, договорившись делить пополам суммарное богатство, выпадающее в каждом из состояний. В подобном случае ожидаемая полезность каждого индивида превысит первоначальный уровень(в предположении, что индивиды несклонны к риску, т.е. функция u(W) вогнута) :

Еu(2) =(1 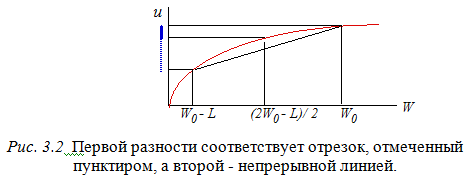-)²u(W₀ )+ ²u(W₀ - L) + 2(1-)u((2W₀ - L)/2) ,
Еu(2) - Еu(1) =(1-)u(W₀) (1-)u(W₀ - L) + 2(1-)u((2W₀ - L)/2) =

(1-) {[u((2W₀ - L)/2) - u(W₀ - L)] - [u(W₀ ) - u((2W₀ - L)/2)]} > 0


Увеличение числа индивидов повышает ожидаемую полезность каждого за счет сокращения возможных колебаний в уровне дохода( получение индивидом низкого или же высокого дохода в подобном случае менее вероятно, чем прежде, ибо неудача одного может быть смягчена выигрышем другого). Собственно, при сохранении прежнего математического ожидания выигрыша индивиды сталкиваются с меньшим разбросом выигрышей( т.е. менее рискованной игрой или игрой, стохастически второго рода доминирующей исходную). Например, если каждый из двух индивидов может с вероятностями 0.5 выиграть 1 или же не получить ничего, то объединение рисков или переход к лотерее

0.25 о 0 0.5 о 1/2 0.25 о 1 ,

не сказавшись на уровне математического ожидания выигрыша, снизит дисперсию. Для не склонного к риску индивиду подобные изменения влекут за собой возрастание уровня ожидаемой полезности.

Возрастание числа индивидов, объединяющих свои риски, естественно, будет повышать уровень их ожидаемой полезности сходным образом.
Однако следует обратить внимание на то обстоятельство, что в подобной ситуации суммарное богатство варьируется в зависимости от того, какое из состояний реализовалось, и, следовательно, существуют социальные или системные риски. Предоставление полной страховки всем индивидам становится и не возможным и не эффективным.

Невозможным - поскольку для этого нужно было бы иметь сумму вдвое превышающую математическое ожидание выигрыша каждого индивида, т.е.

2 (W₀ - L), а эта величина может оказаться как больше, так и меньше выражения, стоящего в предпоследнем столбце приведенной таблицы.
Неэффективным - поскольку контрактная кривая (в общем случае, т.е. при несклонности к риску обоих контрагентов) более не совпадает с линиями уверенности.
Спрос на страхование.

Как несклонность к риску влияет на поведение человека? Не склонный к риску человек интересуется не только ожидаемой величиной потерь, но и возможным размером потерь. Не склонный к риску человек сочтет ситуацию, которая чревата 10%-ным риском потери 20 тыс. долл. Более неблагоприятной, чем ситуация, чреватую 100%-ной вероятностью потери 2000 долл., хотя ожидаемая величина потерь во всех случаях одинаковая. Не склонные к риску стороны не любят неопределенности в отношении самой величины потерь.
Существует три способа, с помощью которых не склонный к риску человек может превратить неопределенный исход в определенный. Во-первых, он может купить рыночную страховку. Во-вторых, он может сам застраховать себя, например, отложив некоторую сумму денег, которая потребуется, чтобы покрыть потери. В-третьих, он может использовать возможности, предоставляемые договором, например, при покупке рискованных активов он может предложить за них более низкую цену.




Рассмотрим вариант с покупкой рыночной страховки.

Покупка рыночной страховки
Владелец имеет автомобиль стоимостью 20000 долл. Вероятность угона автомобиля составляет 10%. В табл. 17 показано два возможных варианта благосостояния этого человека: со страховкой и без нее. Решение приобрести страховку не влияет на его ожидаемое благосостояние, оно по-прежнему составляет 18 тыс. долл.
Приобретение страховки не изменяет ожидаемого благосостояния, однако страховка способствует достижению более высокого уровня полезности для владельца автомобиля.
Владелец автомобиля — это сторона, не склонная к риску. Если риск несет не склонная к риску сторона, то это приведет к большему сокращению ожидаемой полезности дохода, чем несение риска менее склонной или нейтральной стороной. Поэтому та сторона, которая обнаруживает

большую несклонность к риску, может заплатить менее несклонной или нейтральной к риску стороне за то, чтобы та приняла риск на себя, и обе стороны окажутся в более благоприятном положении, с точки зрения ожидаемой полезности. Владелец автомобиля будет готов заплатить

100 долл. за то, чтобы превратить неопределенное будущее в определенное, и его готовность платить говорит о том, что он не склонен к риску.
Страхование позволяет индивиду обменять риск больших потерь на определенность малых потерь.
Если имеются не склонные к риску стороны, то это означает, что распределение риска само по себе влияет на богатство общества.

Предположим, что благосостояние общества — это сумма ожидаемых полезностей сторон. Перераспределение риска от не склонных к риску к нейтральным к риску сторонам приведет к повышению богатства общества.
Общественное благосостояние повышается не только когда риск полностью перекладывается с более несклонной к риску стороны на менее несклонную или нейтральную к риску сторону, но и когда риски делятся между не склонными к риску сторонами.