учебник по ахд. учебник по АХД. Г. В. Савицкая Анализ хозяйственной деятельности предприятия
 Скачать 7.77 Mb. Скачать 7.77 Mb.
|
ее закону нормального распределения. Согласно этому закону, основная масса исследуемых сведений по каждому показателю должна быть сгруппирована около ее среднего значения, а объекты с очень маленькими значениями или с очень большими должны встречаться как можно реже. График нормального распределения информации имеет следующий вид (рис. 7.1). 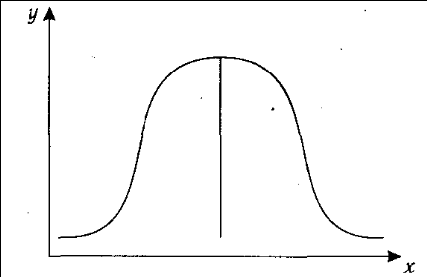 Рис. 7.1. График нормального распределения информации Для количественной оценки степени отклонения информации от нормального распределения служит отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке. Показатель асимметрии (А)и его ошибка (та)рассчитываются по следующим формулам: A = Показатель эксцесса (Е)и его ошибка (те)рассчитываются следующим образом: E = В симметричном распределении А = 0. Отличие от нуля указывает на наличие асимметрии в распределении данных около средней величины. Отрицательная асимметрия свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются значительно реже. Положительная асимметрия показывает, что чаще встречаются данные с небольшими значениями. В нормальном распределении показатель эксцесса Е = 0. Если Е > 0, то данные густо сгруппированы около средней, образуя островершинность. Если Е < 0, то кривая распределения будет плосковершинной. Однако когда отношения А/mаи Е/теменьше 3, то асимметрия и эксцесс не имеют существенного значения и исследуемая информация подчиняется закону нормального распределения. В нашем примере (табл. 7.4) во всех случаях отношения А/mаи Е/те не превышают 3. Значит, исходная информация соответствует этому закону. После отбора факторов и оценки исходной информации важной задачей в корреляционном анализе является моделирование связи между факторными и результативными показателями, т.е. подбор соответствующего уравнения, которое наилучшим образом описывает изучаемые зависимости. Для его обоснования используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. Если связь всех факторных показателей с результативным носит прямолинейный характер, то для записи этих зависимостей можно использовать линейную функцию: Yх = а + b1х1 + b2х2 + b3х3+ ... + bnхn . (7.15) Если связь между результативным и факторными показателями носит криволинейных характер, то может быть использована степенная функция: Yх = или логарифмическая: lgYx = b0 + b1lg x1 + b2lg x2 + … + bnlg xn. (7.17) Приведенные модели выгодны тем, что их параметрам можно дать экономическое объяснение {интерпретацию). В линейной модели коэффициенты показывают, на сколько единиц изменяется результативный показатель с изменением факторного на единицу в абсолютном выражении, в степенных и логарифмических — в процентах. В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. § 7.4). Изучение взаимосвязей между исследуемыми факторами и уровнем рентабельности показало, что все зависимости в нашем примере имеют прямолинейный характер. Поэтому для их описания использована линейная функция. Решение задачи многофакторного корреляционного анализа проводится на ПЭВМ по типовым программам. Сначала формируется матрица исходных данных (табл. 7.5), в первой колонке которой записывается порядковый номер наблюдения, во второй — результативный показатель (у),а в следующих — факторные показатели (xi). Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации. Т а б л и ц а 7.5 Исходные данные для корреляционного анализа
Изучая матрицы парных и частных коэффициентов корреляции, можно сделать вывод о тесноте связи между изучаемыми явлениями. Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учетом взаимодействия с остальными факторами, определяющими уровень результативного показателя. Данные табл. 7.6 (первый столбец) свидетельствуют о том, что все факторы оказывают ощутимое воздействие на уровень рентабельности. Особенно тесная связь рентабельности с материалоотдачей, фондоотдачей, качеством продукции и производительностью труда. С увеличением данных показателей уровень рентабельности повышается (прямая связь). При увеличении продолжительности оборота средств рентабельность снижается (обратная связь). Матрица парных коэффициентов корреляции Т а б л и ц а 7.6
Однако необходимо отметить, что парные коэффициенты корреляции получены при условии воздействия других факторов на результат. Чтобы абстрагироваться от их влияния и получить количественную характеристику связи между результативным и факторными показателями в чистом виде, рассчитываются частные коэффициенты корреляции (табл. 7.7). При сравнении частных коэффициентов корреляции с парными видно, что влияние других факторов на тесноту связи между уровнем рентабельности и исследуемыми факторами довольно значимое: частные коэффициенты корреляции намного ниже парных. Это говорит о том, что факторы, которые входят в данную корреляционную модель, оказывают на рентабельность не только непосредственное влияние, но и косвенное. Поэтому взаимосвязи, очищенные от влияния сопутствующих факторов, получились менее тесными. В некоторых случаях они могут оказаться более тесными, если исключить влияние факторов, которые действуют в противоположном направлении. По этой причине может измениться не только величина коэффициента корреляции, но и направление связи: в общем виде связь может быть прямой, а в чистом — обратной, и наоборот. Объясняется это тем, что при расчете парных коэффициентов корреляции изучается взаимосвязь между результативным и факторным показателем с учетом их взаимодействия и с другими факторами. Например, с повышением уровня оплаты труда рентабельность увеличивается, если темпы роста производительности труда обгоняют темпы роста его оплаты. Поэтому в общем виде взаимосвязь между уровнем рентабельности и уровнем оплаты труда будет прямой. Если взять непосредственную связь между этими показателями при условии неизменности производительности труда и других факторов, то получится, что при повышении оплаты труда рентабельность понижается. Здесь уже обратная зависимость и частный коэффициент корреляции будет со знаком минус. Т а б л и ц а 7.7 Матрица частных коэффициентов корреляции
Таким образом, с помощью парных и частных коэффициентов корреляции можно получить представление о тесноте связи между изучаемыми явлениями в общих и непосредственных соприкосновениях. Значительный интерес представляют коэффициенты корреляции, характеризующие взаимосвязь факторов между собой. Как уже отмечалось, в корреляционную модель надо подбирать независимые между собой факторы. Если коэффициент корреляции двух факторов выше 0,85, то один из них необходимо исключить из модели. Исследование матрицы коэффициентов корреляции позволяет сделать вывод, что в данную модель включены факторы, не очень тесно связанные между собой. При изучении тесноты связи надо иметь в виду, что величина коэффициентов корреляции является случайной, зависящей от объема выборки. Известно, что с уменьшением количества наблюдений надежность коэффициентов корреляции падает, и наоборот, при увеличении количества наблюдений надежность коэффициентов корреляции возрастает. Значимость коэффициентов корреляции проверяется по критерию Стьюдента: t = где σr — среднеквадратическая ошибка коэффициента корреляции, которая определяется по формуле σr = Если расчетное значение t выше табличного, то можно сделать заключение о том, что величина коэффициента корреляции является значимой. Табличные значения t находят по таблице значений критериев Стьюдента. При этом учитываются количество степеней свободы V = (n – 1) и уровень доверительной вероятности (в экономических расчетах обычно 0,05 или 0,01). В нашем примере количество степеней свободы равно n – 1 = 40 – 1 = 39. При уровне доверительной вероятности P = 0,05; t = 2,02. Поскольку t-фактическое (табл. 7.8)во всех случаях выше t-табличного, связь между результативным и факторными показателями является надежной, а величина коэффициентов корреляции — значимой. Т а б л и ц а 7.8 Фактические значения критерия Стьюдента
Следующий этап корреляционного анализа — расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный показатель, потом второй, третий и т.д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, F-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей. Чем выше величина коэффициентов множественной корреляции, детерминации и критерия Фишера и чем ниже величина стандартной ошибки, тем точнее уравнение связи описывает зависимости, сложившиеся между исследуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то надо их отбросить, т.е. остановиться на том уравнении, где эти показатели наиболее оптимальны. Сравнивая результаты на каждом шаге (табл.7.9), мы можем сделать вывод, что наиболее полно описывает зависимости между изучаемыми показателями пятифакторная модель, полученная на пятом шаге. В результате уравнение связи имеет вид Yх= 0,49 +3,65x1 +0,09x2 + 1,02x3 – 0,122x4 + 0,052x5. Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности других. В данном случае можно дать следующую интерпретацию полученному уравнению: рентабельность повышается на 3,65 % при увеличении материалоотдачи на 1 руб.; на 0,09 % — с ростом фондоотдачи на 1 коп.; на 1,02 % — с повышением среднегодовой выработки продукции на одного работника на 1 тыс. руб.; на 0,052 % — при увеличении удельного веса продукции высшей категории качества на 1%. С увеличением продолжительности оборота средств на 1 день рентабельность снижается в среднем на 0,122 %. Таблица 7.9 Результаты расчета уравнения связи
Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, другими словами, рассчитывают стандартизированные коэффициенты регрессии. Их еще называют бетта-коэффициентами по символу, который принят для их обозначения (β). Бетта-коэффициенты и коэффициенты регрессии связаны следующим отношением: βi = Бетта-коэффициенты показывают, что если величина фактора увеличится на одно среднеквадратическое отклонение, то соответствующая зависимая переменная увеличится или уменьшится на долю своего среднеквадратического отклонения. Сопоставление бетта-коэффициентов позволяет сделать вывод сравнительной степени воздействия каждого фактора на величину результативного показателя. В нашем примере наибольшее влияние на уровень рентабельности оказывают материалоотдача, фондоотдача и производительность труда (табл. 7.10); По аналогии можно сопоставить и коэффициенты эластичности, которые рассчитываются по формуле Э = Коэффициенты эластичности показывают, на сколько процентов в среднем изменяется функция с изменением аргумента на 1%. Т а б л и ц а 7.10 Коэффициенты эластичности и бетта-коэффициенты
Согласно данным табл. 7.10, рентабельность возрастает на 0,374% при увеличении уровня материалоотдачи на 1%, на 0,308% — при повышении фондоотдачи на 1% и т.д. 7.4. Методика оценки и практического применения результатов корреляционного анализа Необходимость оценки уравнения связи. Показатели, которые применяются для оценки уравнения связи. Методика их расчета и интерпретация. Использование уравнения связи для оценки деятельности предприятия, определения влияния факторов на прирост результативного показателя подсчета резервов и планирования его уровня. Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации коэффициенты множественной корреляции (R)и детерминации (D). Критерий Фишера рассчитывается следующим образом: F= где ух— среднее значение результативного показателя, рассчитанное по уравнению; т — количество параметров в уравнении связи, учитывая свободный член уравнения; п — количество наблюдений (объем выборки). Фактическая величина F-отношения сопоставляется с табличной и делается заключение о надежности связи. В нашем примере величина F-отношения на пятом шаге равна 95,67.F-теоретическое рассчитано по таблице значений F. При уровне вероятности Р = 0,05 и количестве степеней свободы [(т - 1) = (6 – 1) = 5, (n – т ) = 40 – 6 = 34] оно будет составлять 2,49. Поскольку Fфакт > Fтабл , то гипотеза об отсутствии связи между рентабельностью и исследуемыми факторами отклоняется. Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации: 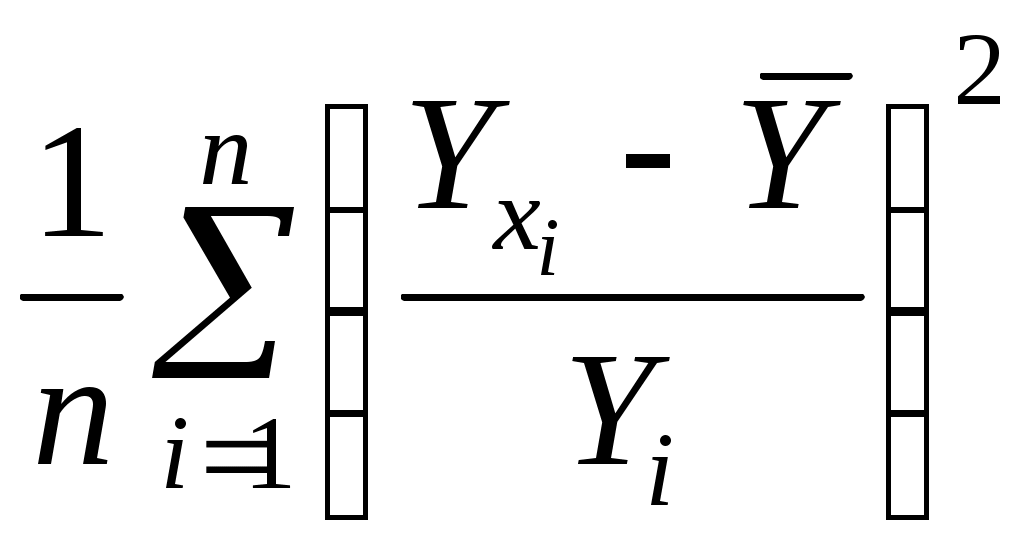 . (7.23) . (7.23)Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64%. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделатьвывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости. С такой же небольшой погрешностью будет делаться и прогноз уровня рентабельности по данному уравнению. О полноте связи можно судить также по величине множественных коэффициентов корреляции и детерминации. В нашем примере на последнем шаге R = 0,92, a D = 0,85. Это значит, что вариация рентабельности на 85% зависит от изменения исследуемых факторов, а на долю других факторов приходится 15% вариации результативного показателя. Значит в корреляционную модель рентабельности удалось включить наиболее существенные факторы. Следовательно, данное уравнение можно использовать для практических целей: а) оценки результатов хозяйственной деятельности; б) расчета влияния факторов на прирост результативного показателя; в) подсчета резервов повышения уровня исследуемого показателя; г) планирования и прогнозирования его величины. Оценка деятельности предприятия по использованию имеющихся возможностей проводится сравнением фактической величины результативного показателя с теоретической (расчетной), которая определяется на основе уравнения множественной регрессии. В нашем примере (см.табл. 7.5) на предприятии №1 материалоотдача (х1) составляет 2,4 руб., фондоотдача (х2) — 80 коп., производительность труда (х3) — 8 тыс. руб., продолжительность оборота оборотных средств (х4)— 25 дней, удельный вес продукции высшей категории качества (х5) — 25%. Отсюда расчетная величина рентабельности составит: Yх= 0,49 + 3,65 × 2,4 × 0,09 × 80 + 1,02×8 - 0,122 × 25 +0,052 × 25 = 22,86%. Она превышает фактическую на 0,36%. Это говорит о том, что данное предприятие использует свои возможности несколько хуже, чем в среднем все исследуемые предприятия. Влияние каждого фактора на прирост (отклонение от плана) результативного показателя рассчитывается следующим образом: В связи с тем что план был недовыполнен по всем факторным показателям (табл. 7.11), уровень рентабельности понизился на 2,095%. Т а б л и ц а 7.11 Расчет влияния факторов на прирост уровня рентабельности
Подсчет резервов повышения уровня рентабельности проводится аналогичным способом: резерв прироста каждого факторного показателя умножается на величину соответствующего коэффициента регрессии: Если предприятие достигнет запланированного уровня факторных показателей (табл. 7.12), то рентабельность повысится на 3,08%, в том числе за счет роста материалоотдачи на 1,09%,"фондоотдачи — на 0,45% и т.д. Так определяют резервы при условии прямолинейной зависимости, когда она отражается уравнением прямой. При криволинейных зависимостях между исследуемыми показателями, которые описываются уравнением параболы, гиперболы и другими функциями, для определения величины резерва роста (снижения) результативного показателя необходимо в полученное уравнение связи подставить сначала фактический уровень факторного показателя, а затем возможный (прогнозный) и сравнить полученные результаты. Например, нужно определить резерв увеличения среднечасовой выработки рабочих, если их средний возраст снизится с 45 до 40 лет. Используя уравнение параболы (см. с. 131), сначала рассчитаем среднюю выработку фактическую: Yф = –2,67 + 4,424 × 4,5 – 0,561 × 4,52 = 5,87 тыс. руб., а затем прогнозируемую: Yn = –2,67 + 4,424 × 4,0 – 0,561 × 4,02 = 6,05 тыс. руб., Сопоставив полученные величины, узнаем резерв роста среднечасовой выработки: Р ↑ Y = Yп – Yф = 6,05 – 5,87 = + 0,18 тыс. руб. Результаты многофакторного регрессионного анализа могут быть также использованы для планирования и прогнозирования уровня результативного показателя. С этой целью необходимо в полученное уравнение связи подставить прогнозный уровень факторных показателей (табл. 7.12). Yпл = 0,49 + 3,65 × 2,7 + 0,09 × 85 + 1,02 × 8,5 – 0,122 × 20 + 0,052 × 33 = 25,95 % Т а б л и ц а 7.12 Подсчет резервов повышения уровня рентабельности
Таким образом, многофакторный корреляционный анализ имеет важную научную и практическую значимость. Он позволяет изучить закономерности изменения результативного показателя в зависимости от поведения разных факторов, определить их влияние на величину результативного показателя, установить, какие из них являются основными, а какие второстепенными. Этим достигается более объективная оценка деятельности предприятия, более точное и полное определение внутрихозяйственных резервов и прогнозного уровня показателей. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
