ТЕСТЫ_МАТ_v_1.2.1_стомат. Гбоу впо тверская гма минздрава России Кафедра физики, математики и медицинской информатики Физика, математика

• Название: Гбоу впо тверская гма минздрава России Кафедра физики, математики и медицинской информатики Физика, математика
• Дата: 16.02.2022
• Размер: 387.5 Kb.
• Имя файла: ТЕСТЫ_МАТ_v_1.2.1_стомат.doc
• Тип: Сборник; #363953
• страница: 1 из 3

ГБОУ ВПО Тверская ГМА Минздрава России

Кафедра физики, математики и медицинской информатики


«Физика, математика»

Модуль: «Математика»

Задания в тестовой форме для рубежного контроля знаний

студентов, обучающихся по специальности

«Стоматология»


Тверь 2014

Авторы-составители: зав.кафедрой физики, математики и медицинской информатики доцент, к.ф.-м.н. В.В. Туровцев, доцент, к.ф.-м.н. В.И. Бахтилов, доцент, к.ф.-м.н. О.М. Корпусов, доцент, к.ф.-м.н. А.Б. Залетов, профессор, д.т.н. Ю.В. Богданов, ст. преподаватель Е.Н. Гординская, ассистент Е.В. Крючкова.
Рецензенты: доцент кафедры химии и биохимии, к.х.н. Н.П. Лопина,

доцент кафедры биологии, к.б.н. Е.А. Харитонова.


Задания для рубежного контроля рекомендованы ЦКМС ТГМА для использования в учебном процессе по специальности 060201 «Стоматология». Сборник тестовых заданий предназначен для самостоятельной подготовки студентов 1 курса к лабораторным и итоговым занятиям по дисциплине «Физика, математика».
Содержание

Предисловие 4

1.Критерии оценки рубежного тестового контроля знаний по модулю «Математика» 5

1.1.Критерии оценки выполнения заданий в тестовой форме: 5

2.Оценочные средства текущего контроля 6

2.1.Задания в тестовой форме 6

2.2.Эталоны правильных ответов к заданиям в тестовой форме 22

Основная литература 23

Дополнительная литература 23

Предисловие
Сборник заданий для рубежного контроля составлен в помощь студентам 1 курса стоматологического факультета при подготовке к лабораторным и итоговым занятиям по дисциплине «Физика, математика». Он включает в себя: характеристику используемых форм рубежного контроля, критерии оценок, а также основные оценочные средства.

Сборник заданий составлен в соответствии с требованиями Федерального ГОС по специальностям 060201 «Стоматология» (Москва, 2011 г.), Типовой учебной программой дисциплины «Физика, математика» (Москва, 2011 г.) и рекомендациями Центра тестирования (Москва, 2006 г.).

1. 
   Критерии оценки рубежного тестового контроля знаний по модулю «Математика»
   
   1. 
      Критерии оценки выполнения заданий в тестовой форме:
      

Студентом даны правильные ответы на задания в тестовой форме (25 тестовых заданий):

70% и менее – оценка «не зачтено»

71% - 100% заданий – оценка «зачтено»

2. 
   Оценочные средства текущего контроля
   
   1. 
      Задания в тестовой форме
      

ЧАСТЬ 1

Инструкция. Выберите один верный ответ или правильно продолжите фразу.

1. 
   Укажите формулу классического определения вероятности случайного события А (n-общее число исходов, m-число благоприятных исходов для события А).
   
   1. 
      
      
   2. 
      
      
   3. 
      
      
   4. 
      
      

2. 
   Как называется случайное событие, вероятность которого равна нулю?
   

3. 
   Как называется случайное событие, вероятность которого равна единице?
   

4. 
   События называют совместными, если:
   
   1. 
      наступление одного из событий в одном опыте не исключает появление другого
      
   2. 
      наступление одного из них в одном опыте обязательно сопровождается наступлением другого
      
   3. 
      в условиях опыта произойдут только эти события и никакие другие
      
   4. 
      если события не могут произойти одновременно в условиях данного опыта
      

5. 
   События называют единственно возможными:
   
   1. 
      если в условиях данного опыта произойдут только эти события и никакие другие
      
   2. 
      если наступление одного из событий в одном опыте исключает появление другого
      
   3. 
      если события не могут произойти одновременно в условиях данного опыта
      
   4. 
      наступление одного из событий в одном опыте не исключает появление другого
      

6. 
   Статистическая вероятность события численно равна (n-общее число исходов, m-число исходов для события А):
   
   1. 
      
      
   2. 
      
      
   3. 
      
      
   4. 
      
      

7. 
   Суммой двух событий A и B является событие C, которое заключается:
   
   1. 
      в появлении либо события А, либо события В
      
   2. 
      в одновременном появлении событий А и В
      
   3. 
      в исключении события А и события В
      
   4. 
      в непоявлении события А и появлении события В
      

8. 
   Произведением двух событий A и B является событие С, которое заключается:
   
   1. 
      в исключении события А и события В
      
   2. 
      в появлении либо события А, либо события В
      
   3. 
      в одновременном появлении событий А и В
      
   4. 
      в непоявлении события А и появлении события В
      

9. 
   Вероятность суммы двух совместимых событий равна:
   
   1. 
      P (A или B) = P(A)+ P(B)- P(A и B)
      
   2. 
      P (A или B) = P(A)+ P(B)+ P(A и B)
      
   3. 
      P (A или B) = P(A)+ P(B)
      
   4. 
      P(A или B) = P(A)+P(B)*P(B/A)
      

10. 
    Вероятность суммы двух несовместимых событий равна:
    
    1. 
       P (A или B) = P(A)+P(B)-P(A)*Р(B)
       
    2. 
       P (A или B) = P(A)+P(B)+P(A)*Р(B)
       
    3. 
       P (A или B) = P(A)+P(B)
       
    4. 
       P(A или B) = P(A)+P(B)*P(B/A)
       

11. 
    Вероятность произведения двух независимых событий равна:
    
    1. 
       P(AиB) = P(A)*P(B)
       
    2. 
       P(AиB) = P(A)+Р(В)*P(B/A)
       
    3. 
       P(AиB) = P(A)*P(B)*P(B/A)
       
    4. 
       P(AиB) = P(A)*P(B)-P(AB)
       

12. 
    Вероятность произведения двух зависимых событий равна:
    
    1. 
       P(AиB) = P(A)*P(B)
       
    2. 
       P(AиB) = P(A)*P(B/A)
       
    3. 
       P(AиB) = P(A)*P(B)*P(B/A)
       
    4. 
       P (AиB) = P(A)* P(B)- P(AB)
       

13. 
    Случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями, называют
    

14. 
    Случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка, называют
    

15. 
    Дисперсия характеризует:
    
    1. 
       наименьшее значение случайной величины
       
    2. 
       среднее значение случайной величины
       
    3. 
       степень рассеяния случайной величины относительно её математического ожидания
       
    4. 
       степень рассеяния случайной величины относительно её моды
       

16. 
    Дисперсия дискретной случайной величины рассчитывается по формуле:
    
    1. 
       
       
    2. 
       
       
    3. 
       
       
    4. 
       
       

17. 
    Дисперсия непрерывной случайной величины рассчитывается по формуле:
    
    1. 
       
       
    2. 
       
       
    3. 
       
       
    4. 
       
       

18. 
    Дискретная случайная величина не подчиняется:
    
    1. 
       распределению Пуассона
       
    2. 
       нормальному распределению
       
    3. 
       биноминальному распределению
       
    4. 
       распределению Бернулли
       

19. 
    Математическим ожиданием случайной величины называется:
    
    1. 
       сумма произведений всех возможных значений случайной величины на соответствующие им вероятности
       
    2. 
       корень квадратный из дисперсии
       
    3. 
       совокупность всех значений этой величины с соответствующими вероятностями
       
    4. 
       сумма квадрата произведений всех возможных значений случайной величины на соответствующие им вероятности
       

20. 
    Математическое ожидание дискретной случайной величины рассчитывается по формуле:
    
    1. 
       
       
    2. 
       
       
    3. 
       
       
    4. 
       
       

21. 
    Математическое ожидание непрерывной случайной величины рассчитывается по формуле:
    
    1. 
       
       
    2. 
       
       
    3. 
       
       
    4. 
       
       

22. 
    Среднее квадратичное отклонение дискретной случайной величины рассчитывается по формуле:
    
    1. 
       
       
    2. 
       
       
    3. 
       
       
    4. 
       
       

23. 
    Среднее квадратичное отклонение непрерывной случайной величины рассчитывается по формуле:
    
    1. 
       
       
    2. 
       
       
    3. 
       
       
    4. 
       
       

24. 
    Установите правильную последовательность следующих этапов статистической работы:1.обработка данных 2.сбор данных 3.выводы, прогнозы.
    
    1. 
       123
       
    2. 
       132
       
    3. 
       231
       
    4. 
       213
       

25. 
    Коэффициент Стьюдента находят из таблицы по значениям:
    
    1. 
       доверительной вероятности и среднего значения
       
    2. 
       уровня значимости и среднеквадратического отклонения
       
    3. 
       доверительной вероятности и объёма выборки
       
    4. 
       доверительной вероятности и уровня значимости
       

26. 
    Зависимость называется функциональной, если:
    
    1. 
       одному значению одной переменной величины соответствует множество значений другой
       
    2. 
       одному значению одной переменной величины соответствует одно значение другой
       
    3. 
       одному значению одной переменной величины соответствует два значения другой
       
    4. 
       одному значению одной переменной величины не соответствует ни одно значение другой
       

27. 
    Если одному значению одной переменной соответствует множество значений другой, то такая зависимость называется:
    
    1. 
       функциональной
       
    2. 
       обратно пропорциональной
       
    3. 
       статистической
       
    4. 
       прямо пропорциональной
       

28. 
    Метод регрессии позволяет установить:
    
    1. 
       зависимость между изменчивостью признаков
       
    2. 
       меру тесноты связи двух переменных
       
    3. 
       количественное изменение среднего значения одной величины по мере изменения другой
       
    4. 
       доверительную вероятность и среднее значение
       

29. 
    Линейный коэффициент корреляции определяется по формуле: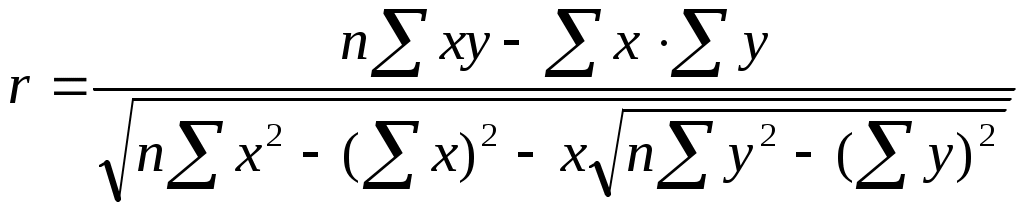
    
    1. 
       
       
    2. 
       
       
    3. 
       
       
    4. 
       
       

30. 
    По формуле находят:
    
    1. 
       дисперсию выборки
       
    2. 
       среднее значение выборки
       
    3. 
       генеральную совокупность
       
    4. 
       среднее квадратическое отклонение
       

31. 
    По формуле 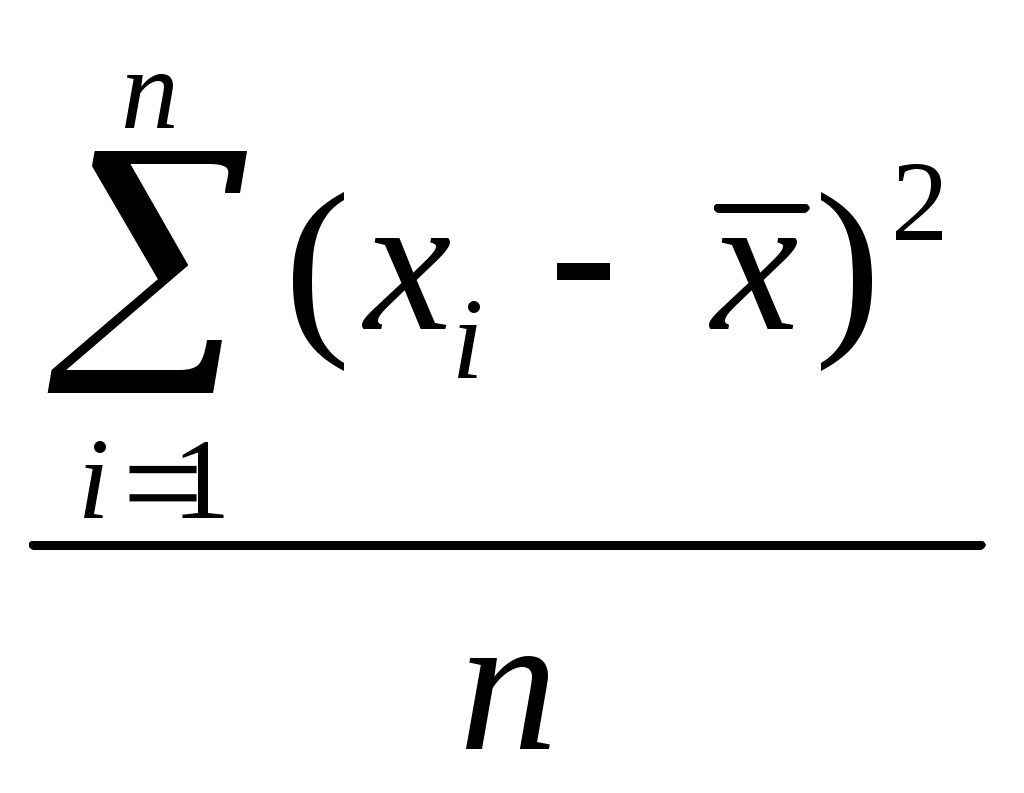находят:
    
    1. 
       среднее значение выборки
       
    2. 
       дисперсию выборки
       
    3. 
       среднее отклонение случайной величины
       
    4. 
       коэффициент корреляции
       

32. 
    Статистическая совокупность, которая включает в себя все изучаемые объекты, называется:
    
    1. 
       представительной выборкой
       
    2. 
       генеральной совокупностью
       
    3. 
       статистическим рядом
       
    4. 
       вариационным рядом
       

33. 
    Статистическая совокупность, которая включает в себя не все изучаемые объекты, а лишь их часть, называется:
    
    1. 
       выборкой
       
    2. 
       генеральной совокупностью
       
    3. 
       статистическим рядом
       
    4. 
       вариационным рядом
       

34. 
    Интервал возможных значений искомого параметра, в котором могут находиться с некоторой вероятностью его значения, называется:
    
    1. 
       доверительным интервалом
       
    2. 
       вариационным интервалом
       
    3. 
       корреляционным интервалом
       
    4. 
       представительным интервалом
       

35. 
    Коэффициент линейной корреляции может принимать значения:
    
    1. 
       от до
       
    2. 
       от до
       
    3. 
       от 0 до 1
       
    4. 
       от до +1
       

36. 
    Коэффициент, характеризующий силу статистической линейной связи между случайными величинами, называется:
    
    1. 
       коэффициентом корреляции
       
    2. 
       коэффициентом регрессии
       
    3. 
       коэффициентом вариации
       
    4. 
       коэффициентом дисперсии