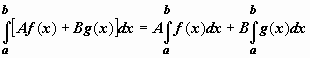Геометрический и механический смысл производной

• Название: Геометрический и механический смысл производной
• Анкор: otvety.doc
• Дата: 19.03.2019
• Размер: 0.63 Mb.
• Имя файла: otvety.doc
• Тип: Документы; #26119

1)Производная. Пусть функция y=f(x) определена на некоторой окрестности точки xₒ. Дадим аргументу xₒ некоторое приращение ∆x(положительное или отрицательное). Тогда функция y=f(x) получит приращение: ∆y=f(xₒ+∆x)-f(xₒ). Рассмотрим отношение : ∆y /∆x=(f(xₒ+∆x)-f(xₒ))/∆x. Определение : Конечный предел отношения приращения ∆y к вызвавшему его приращению ∆x, когда ∆x→0, называется производной функции f(x) в точке xₒ. Этот предел обозначается символом f ‘ (xₒ) :

Геометрический и механический смысл производной: Если функция  имеет конечную производную в точке x₀, то в окрестностиU(x₀) её можно приблизить линейной функциейФункция f_l называется касательной к f в точке x₀. Число  является угловым коэффициентом или тангенсом угла наклона касательной прямой.

2)Дифференцируемость функции в точке : Производная  функции f в точке x₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x₀ тогда и только тогда, когда её производная в этой точке существует и конечна:Для дифференцируемой в x₀ функции f в окрестности U(x₀) справедливо представление при .Критерий дифференцируемости: пусть функция f(x) определена в некотором интервале (а, b) и , тогда функция f(x) дифференцируема в точке  тогда и только тогда, когда у неё в точке  существует производная..Необходимое условие дифференцируемости : Если функция f(x) дифференцируема в точке x₀, то она непрерывна в этой точке.

Из непрерывности самой функции в точке x₀ не следует дифференцируемость ее в этой точке.
3)Арифметические свойства дифференцируемых функций(дифференциал суммы ,произведения и частного) : Если функции f(x) и g(x) дифференцируемы в точке xₒ , то и функции C1f(x) + C2g(x) , где С1 и С2 – постоянные числа, f(x)g(x) дифференцируемы в точке xₒ , причем в этой точке d(C1f(x)+C2g(x))=C1df+C2dg ; d(fg)=gdf+fdg ; d(f/g)=(gdf-fdg) / (g^2).
4)Теорема о производной сложной функции: Если функция u= u(x) имеет в некоторой точке x₀ производную  и принимает в этой точке значениеu₀ = u(x₀), а функция y= f(u) имеет в точке u₀ производную y '_u= f '(u₀), то сложная функция y = f(u(x)) в указанной точке x₀тоже имеет производную, которая равна y '_x= f '(u₀)·u '(x₀), где вместо u должно быть подставлено выражение u= u(x).Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. 
Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:

Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.Отсюда видно, что искомая производная равна

5)Дифференциа́л — линейная часть приращения функции. Дифференциал функции  в точке  может быть определён как линейная функциягде f'(x₀) обозначает производную f в точке x₀.Таким образом df есть функция двух аргументов .Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция  линейно зависящая от h и для которой верно следующее соотношение Свойства дифференциала:1. Постоянный множитель можно вынести за знак дифференциала: 
2. дифференциал алгебраической суммы функций равен алгебраической сумме дифференциалов этих функций 
3. дифференциал произведения 
4. дифференциал дроби (дифференциал частного) 
5. дифференциал сложной функции  
где d g(x), в свою очередь, можно дифференцировать дальше.

6)Локальные экстремумы функций : точка xₒ (в которой функция f(x) непрерывная) называется точкой локального максимума(или минимума) функции f(x), если существует такая окрестность б(xₒ) точки xₒ , что для все x пренадлежащих б(xₒ); f(x) ≤ f(xₒ); (f(x)≥ f(xₒ)). Точки локального максимума и локального минимума называются точками экстремума. Значение функции в этих точках называются экстремумами функции.Необходимое условие локального экстремума : если точка xₒ - точка экстремума функции f(x) ,Ю то в этой точке производная функции f(x) либо равна 0 , либо не существует.

7)Свойства функций ,непрерывных на отрезке: Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее. Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b. Теорема 3 (теорема о промежуточных значениях). Пусть функция y = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C.

Теорема Ро́лля (теорема о нуле производной) утверждает, что если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
8)Теорема Лагра́нжа  Пусть функция f(x )непрерывна на отрезке [a, b]; дифференцируема в интервале (a, b).Тогда существует точка с  (a, b) такая, что f(b) − f(a) = f '(c) · (b − a) .

Теорема Коши : Пусть даны две функции  и  такие, что:1) и  определены и непрерывны на отрезке ;2)производные  и  конечны на интервале ;3)производные  и  не обращаются в нуль одновременно на интервале 4);Тогда , где (Если убрать условие 4, то необходимо усилить условие 3: g'(x) не должна обращаться в ноль нигде в интервале (a,b).) Для доказательства введём функцию Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а  равна как раз необходимому числу.
9)Условия возрастания и убывания дифференцируемой на интервале функции:Пусть функция  дифференцируема на интервале  и  при всех . Тогда  возрастает на . Если же  при всех , то  не убывает на .Аналогично, если  при всех , то  убывает на , а если  при всех , то  не возрастает на . Если дифференцируемая функция не убывает на интервале , то  при всех ; если же функция не возрастает на , то при .


10)Локальный экстремум : Слово «локальный» подчеркивает, что речь идет об экстремуме функции в достаточно малой окрестности рассматриваемой точки. Таким образом, локальный максимум (минимум) – это наибольшее (соответственно наименьшее) значение функции в некоторой достаточно малой окрестности рассматриваемой точки.Заметим, что речь может идти как о функции одного, так и нескольких переменных.Для соответствующих глобальных характеристик вместо слов «экстремум», «максимум», «минимум» обычно употребляют термины «наибольшее значение функции» и «наименьшее значение функции» на соответствующем множестве..
 Достаточные условия экстремума.Пусть функция дифференцируема в некоторой окрестности точки x₀, кроме, быть может, самой этой точки, и непрерывна в точке x₀. Если производная функции меняет знак с минуса на плюс при переходе через эту точку слева направо, то x₀ – точка минимума. Если производная функции меняет знак с плюса на минус при переходе через эту точку слева направо, то x₀ – точка максимума.Пусть  – стационарная точка функции f (x), и существует  Если  то  – точка минимума; если  то  – точка максимума функции f (x).Так, производная функции f (x) = |x| равна –1 при отрицательных x и +1 при положительных x. Функция |x| достигает в точке x₀ = 0 своего минимума.В точке x₀ = 0 первая производная функции f (x) = –x² равна f ′ (x₀) = –2x₀ = 0, а вторая производная f ′′ (x₀) = (–2x)′ = –2 < 0. Функция –x² + 3 достигает в точкеx₀ = 0 своего максимума.

11)Выпуклость графика функции : График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. Достаточное условие выпуклости : Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x)отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.

12) Точка перегиба графка функции : Пусть функция f(x) имеет непрерывную вторую производную f ''(x) и пусть A[x₀ ; f(x₀ )] - точка перегиба кривой y = f(x). Тогда f ''(x₀ ) = 0 или не существует. Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точкиx₀, имеет в x₀ точку перегиба, то . Второе достаточное условие существования точки перегиба: Если в некоторой точке вторая производная функции равна нулю, а третья не равна нулю, то эта точка является точкой перегиба.

13)Правило Лопиталя  :  метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их. Условия:1) или ;2) и  дифференцируемы в проколотой окрестности ;3) в проколотой окрестности ;4)существует ,тогда существует .Пределы также могут быть односторонними. Доказательство: Отношениебесконечно малых.Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида .Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку  теорему Коши. По этой теореме получим:

,но f(a) = g(a) = 0, поэтому .Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим: для конечного предела и для бесконечного,что является определением предела отношения функций.

14) Асимптоты графика функции : Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.  Теорема   Прямая  служит наклонной асимптотой для графика  при  (или при ) в том и только том случае, когда

(7.2)

и

(7.3)

(соответственно, если и 

Таким образом, для нахождения наклонной (или горизонтальной, если получится ) асимптоты достаточно найти два указанных предела  и, затем, . Прямая  будет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.

Общая схема исследования функции и построения графиков

Найти ОДЗ и точки разрыва функции.Найти точки пересечения графика функции с осями координат.Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.Найти асимптоты графика функции: а) вертикальные, b) наклонные.На основании проведенного исследования построить график функции.

Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.

15)Первообра́зной данной функции f называют такую F,производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием. Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .
F(x) - некоторая первообразная функции f(x), то , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.

16)Задача нахождениянеопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю. формулу интегрирования по частям

   или

С помощью формулы интегрирования по частям вычисляется достаточно большой класс неопределенных интегралов. Во многих случаях, применяя данную формулу, это есть единственный способ вычислить интеграл.

Для применения данной формулы, необходимо подынтегральную функцию разбить на произведение двух функций, одна из которых является производной, далее применить формулу интегрирования по частям. Замена переменной : Положив в  , что  , т.е. переменная  является функцией от  , тогда

получим выражения для  и  . Теперь подставим полученные выражения в интеграл, следовательно:

где  --произвольная постоянная и функция  -- обратная функция к . Такое преобразование интеграла называется интегрированием подстановкой (замена переменных).

Замечание. Последнее действие в предыдущем равенстве является обязательным, т.к. интеграл зависит от переменной  , следовательно, ответ должен быть функцией от  . Это операция называется - обратная замена переменных.

Общая замена переменных выглядит следующим образом:

тогда

и, используя эти равенства, добиваемся, чтобы в исходном интеграле, зависящим от  , не было вхождения  , т.е.



Здесь следуя предыдущему замечанию необходимо сделать обратную замену переменных. Отметим, что если изначально, например, интегрировали по  , то ответ не должен содержать других переменных кроме  .

17)Определенный интегралот функции : Предел от суммы  при  , если он существует и конечен, называется определенным интегралом от функции  в пределах от  до  и обозначается:

Свойства определённого интеграла : 1) Линейность. Если функции y = f(x), y = g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и

2) Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то 3) Теорема об интегрировании неравенств. Если в любой точке  выполняется неравенство  , и функции f(x), g(x)интегрируемы по отрезку [a,b], то .

18)Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то . Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) - непрерывно дифференцируемые функции, то . Замена переменной в определённом интеграле. Теорема. Пусть функция  1)определена, непрерывно дифференцируема и монотонна на отрезке ,2),3)функция  непрерывна на отрезке [a, b].Тогда .

Таблица дифференциалов



19)Производная обратной функции : Пусть  - дифференцируемая функция от аргумента x в некотором интервале . Если в уравнении  y считать аргументом, а x - функцией, то возникает новая функция , где  - функция обратная данной.Пример :Дифференцирование функций, заданных параметрически : Пусть задана зависимость двух переменных  и  от параметра , изменяющегося в пределах от  до :

Пусть функция  имеет обратную: . Тогда мы можем, взяв композицию функций  и , получить зависимость  от : . Зависимость величины  от величины , заданная через зависимость каждой из них от параметра  в виде , называется функцией , заданной параметрически.

Производную функции , заданной параметрически, можно выразить через производные функций  и : поскольку  и, по формуле производной обратной функции, , то



где  -- значение параметра, при котором получается интересующее нас при вычислении производной значение .

Заметим, что применение формулы приводит нас к зависимости между  и , снова выраженной в виде параметрической зависимости: , ; второе из этих соотношений -- то же, что участвовало в параметрическом задании функции . Несмотря на то, что производная не выражена через  в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра .

 


20)Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси  и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла  при  называется несобственным интегралом функции f(x) от a до  и обозначается . 
Итак, по определению, . Если этот предел существует и конечен, интеграл  называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся. Формула Ньютона-Лейбница для несобственного интеграла. В приведённых примерах мы сначала вычисляли с помощью первообразной функции определённый интеграл по конечному промежутку, а затем выполняли предельный переход. Объединим два этих действия в одной формуле. Символом  будем обозначать ; символом  - соответственно, ; тогда можно записать , , , подразумевая в каждом из этих случаев существование и конечность соответствующих пределов. Теперь решения примеров выглядят более просто:  - интеграл сходится;  - интеграл расходится.

Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной: ; при замене переменной несобственный интеграл может преобразовываться в собственный. Так, например, вычислим интеграл: . Пусть  , ; если , то ; если  то ; Поэтому  (это уже собственный интеграл) =  .

21)Вычисление площади в декартовых координатах

Если плоская фигура ограничена прямыми x=a, x=b, a , то ее площадь вычисляется по формуле

 (рис. 1).

Аналогично можно рассматривать фигуру относительно оси ОУ.

В некоторых случаях границы х=а и х=b могут вырождаться в точку пересечения кривых  .

В сложных случаях область следует разбить на фигуры, границы которых удовлетворяют указанным соотношениям.

При решении задач удобно придерживаться следующего порядка:

-  построить в декартовых координатах фигуру, площадь которой требуется найти;

-  найти точки пересечения кривых, образующих границу области для определения пределов интегрирования;

-  записать формулу для вычисления и найти площадь.

Вычисление площади в полярных координатах

Пусть фигура представляет собой сектор, заданный в полярной системе координат кривой  , где  - неотрицательная непрерывная кривая на отрезке  . Разобьем угол  на nчастей лучами  <  <…<  и обозначим  

Площадь криволинейного сектора равна сумме n площадей  , заданных разбиением  , i = 1, 2, …, n, .Выберем один из элементов разбиения  , соответствующий сектору  , и зафиксируем на этом промежутке произвольное значение  . Значение функции  в точке  обозначим  и заменим площадь криволинейного сектора круговым сектором радиуса  , площадь которого  . Выполним такую же операцию на каждом участке разбиения  и просуммируем полученные значения.Сумма площадей круговых секторовпредставляет собой интегральную сумму , предел которой, существующий в силу непрерывности функции  , равен определенному интегралу, выражающему площадь фигуры в полярных координатахПри вычислении площади фигуры в полярных координатах рекомендуется придерживаться такого же порядка исследования, что и в декартовых координатах: построение чертежа, вычисление точек пересечения кривых, образующих границу фигуры; запись формулы.

22)Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси  и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла  при  называется несобственным интегралом функции f(x) от a до  и обозначается . Итак, по определению, . Если этот предел существует и конечен, интеграл  называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся. Признаки сравнения для неотрицательных функций. В этом разделе мы будем предполагать, что все подынтегральные функции неотрицательны на всей области определения. До сих пор мы определяли сходимость интеграла, вычисляя его: если существует конечный предел первообразной при соответствующем стремлении ( или ), то интеграл сходится, в противном случае - расходится. При решении практических задач, однако, важно в первую очередь установить сам факт сходимости, и только затем вычислять интеграл (к тому же первообразная часто не выражается через элементарные функции). Сформулируем и докажем ряд теорем, которые позволяют устанавливать сходимость и расходимость несобственных интегралов от неотрицательных функций, не вычисляя их. 



25)Формула Тейлорапоказывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.



, где R_n(x) - остаточный член формулы Тейлора.

ОСТАТОЧНЫЙ ЧЛЕН ФОРМУЛЫ ТЕЙЛОРА

В форме Лагранжа:В форме Коши:

23-24)Вычисление длины дуги кривой.

Пусть в декартовой системе координат на плоскости дана кривая, являющаяся графиком непрерывной дифференцируемой функции y=f(x) с непрерывной производной на отрезке [a,b]. Разобьем отрезок [a,b] произвольным образом на n частей точками . Найдем значения функции f(x) в точках разбиения. Тогда дуга кривой f(x) на [a,b] разобьется на n частей точками

 . Проведем хорды  и обозначим их длины  соответственно. Полученная ломаная имеет длину  .

 Длиной дуги кривой y=f(x) на отрезке [a,b] называется предел, к которому стремится длина вписанной ломаной при стремлении к нулю длины ее наибольшего звена (или, что то же самое, при неограниченном увеличении числа точек деления) .Длина отдельного звена ломаной может быть найдена как длина отрезка  : .Поскольку функция f(x) непрерывна и дифференцируема на всем промежутке [a,b], то, по теореме Лагранжа о дифференцируемых функциях, найдется такая точка  на отрезке  , что .Если обозначить  , то формулу для  можно переписать в видеТаким образом, длина дуги y=f(x) на отрезке [a,b] определяется формулойв силу непрерывности f’(x) и определения интегральной суммы. Выражение   называется дифференциалом  дуги. Если длина кривой существует и конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая.

Если кривая задана уравнением x=f(y), yÎ[a,b], то, рассуждая аналогично, можно получить формулу ,  .Если кривая на плоскости задана параметрически: x=x(t), y=y(t),  ;  , где x(t), y(t) – дифференцируемые функции, имеющие на отрезке   непрерывную производную, то, выполнив замену переменной в предыдущих формулах, получим: , Если задана пространственная кривая параметрическими уравнениями x=x(t), y=y(t), z=z(t),  , где x(t), y(t), z(t) – дифференцируемые на отрезке функции с непрерывной производной, то длина кривой вычисляется по формуле ,  .Пусть в полярных координатах кривая задана уравнением  , где  - дифференцируемая функция с непрерывной на  производной  . Запишем формулы перехода от декартовой системы координат к полярной:  . Если в эти формулы подставить  , то получится параметрическое задание кривой, где параметр  - полярный угол. Тогда по формуле для параметрически заданной функции можно найти длину дуги кривой . ,  .