Основные понятия химической термодинамики. Характеристика равновесного состояния. Теплота и работа. Внутренняя энергия. Термодинамика изучает законы, которые описывают обмен энергией между изучаемой системой и окружающей средой. Химическая термодинамика-это наука, изучающая переход энергии из одной формы в другую при химических процессах и устанавливающая пределы их самопроизвольного протекания и их направленность. Изучаемая система-совокупность химических в-в, мысленно обособленных от окружающей внешней среды. Гомогенная с-ма-части которой различающиеся по св-вам не имеют видимой границы раздела. Если такая граница имеется, то такая с-ма называется гетерогенной (состоит из двух и более фаз). Фаза - гомогенная часть гетерогенной с-мы. Каждое состояние с-мы хар-ется набором параметров состояния (термодинамических параметров состояния). Изменение хотя бы одного параметра может привести к привести к началу хим. реакции. Св-ва с-мы определяются её равновесным состоянием, при котором со временем не изменяются параметры сос-ния. Важнейшими хар-ками состояния с-мы являются теплота и работа. Если между изучаемой с-мой и окружающей внешней средой возможен обмен энергией и работы, то такая сис-ма называеся открытой. Если не возможен обмен – изолированной. Если возможен только энергообмен – замкнутая. Важнейшей хар-кой состояния с-мы является внутренняя энергия (U)-функция состояния с-мы. Внутренняя энергия-величина, хар-ющая весь внутренний запас энергии, который складывается из энергии поступательного и вращательного движения молекул, колебательной энергии атомов и атомных групп, входящих в состав молекул, энергии вращения электронов, ядерная энергия. Абсолютное значение U определить невозможно. Можно определить только ΔU.
Квантово-механическая теория строения атома. Уравнения Планка и Эйнштейна. Диаметр атома равен 10-8 см. Диаметр ядра от 10-13 до 10-14 см. Основу квантовой механики составляют представления о двойственности поведения микрочастиц. Двойственность заключается в следующем: с одной стороны при одних физических условиях микрочастицы ведут себя как в-ва (имеют четкую траекторию движения, массу, импульс), при других условиях они проявляют волновые св-ва: E=hν – ур-е Планка. E=mc2 – ур-е Эйнштейна. Постулаты Бора: 1) Существуют сос-ния атома водорода, при которых возможно движение электрона относительно ядра без выделения или поглощения энергии. 2) При переходе из одного такого сос-ния в другое атом излучает и поглощает квант энергии.
Современная теория строения атома. Теория Луи де Бройля, принцип неопределенности Гейзенберга, уравнение Шрёдингера. В 1924 г. Луи де Бройль выдвинул идею о том, что элементарная частица, движущаяся с определённой скоростью, может рассматриваться не только как частица, но и как волна с определенной частотой колебаний, удовлетворяя условию равенства энергий. Таким образом возник дуализм: частица обладает не только корпускулярными, но и волновыми св-вами. Шрёдингер рассмотрел поведение внутриатомного электрона и описал его уравнением стоячей волны. В отличие от бегущей волны, стоячая волна не перемещается в пространстве и не переносит энергию, а лишь передает её от одних точек струны к другим. Физический смысл имеет квадрат волновой функции (ψ2), который пропорционален вероятности нахождения электрона в том или ином месте внутриатомного пространства. Если мы рассмотрим мысленно проведенную пов-сть, равную электронной плотности, внутри которой расположено 90% заряда – хроничная пов-сть, её формы и размеры принято считать формами и размерами электронного облака. Вместе с ур-ем Шрёдингера в квантовой механике сущ-ет принцип неопределенности Гейзенберга. Невозможно одновременно точно определить координаты и импульс элементарной частицы.
Квантовые числа. S-, p-, d-, f- элементы. Квантовые числа и их пределы вытекают из ур-я квантово-механической теории. Собственные волновые функции описывают состояние электрона в атоме или орбитали. Орбиталь характеризуется определенными значениями квантовых чисел. При n=1 ур-е Шрёдингера имеет только одно решение 1s. Физический смысл квантовых чисел: n – главное квантовое число, определяющее возможные энергетические состояния электрона в атоме. Главное квантовое число определяет на каком энергетическом уровне находится электрон, характеризует энергию электрона и радиус энергетического уровня. Орбитальное квантовое число определяет значение орбитального магнита, кол-во электронов. Магнитное квантовое число характеризует ориентацию облаков в пространстве. Атомные орбитали – совокупность положений электрона. Атомную Орбиталь графически обозначают в виде квантовой ячейки. Спин – собственный момент вращения, который не связан с орбитальным движением электрона.
Многоэлектронные атомы. Принцип наименьшей энергии. Распределение электронов на энергетических подуровнях подчиняется принципу наименьшей энергии: заполнение электронами атомных орбиталей (энергетических подуровней) происходит таким образом: прежде всего заполняются подуровни с наименьшим уровнем энергии, что соответствует максимальной стабильности атома. С учетом этого, а также электростатического взаимодействия и эффекта экранирования, последовательность заполнения происходит по правилу: 1s2s2p3s3p4s3d4p5s4d5p6s5d4f6p7s6d5f7p.
|
Первый закон термодинамики и его применение при условии постоянного объема и постоянного давления. I закон термодинамики: теплота подведенная к с-ме идет на изменению внутренней энергии и совершение работы самой сис-мой. Многие химические процессы протекают либо при постоянном объеме либо про пост. давлении.(V=const; A=pΔV=0 => ΔU=QV)(p=const; QP=(U2-U1)+p(V2-V1)=(U2-pV2)-(U1+pV1). U+pV-теплосодержание с-мы (энтальпия (Н)). ΔН=Н2-Н1=QP
Правило Гунда и правила Клечковского. Правила Клечковского: 1) при увеличении заряда ядра на 1 последовательность заполнения атомных орбиталей происходит от орбитали с наименьшей суммой n+l к орбитали с большим значением этой суммы 2) при одинаковых суммах n+l последовательность заполненияатомных орбиталей происходит в направлении возрастания главного квантового числа. Правило Гунда: на одном и том же энергетическом подуровне прежде всего электроны стремятся занять свободные орбитали с тем, чтобы их суммарный спин был максимальным.
|
Закон Гесса. Следствия закона Гесса. Стандартная энтальпия образования веществ. Тепловой эффект р-ции не зависит от пути её протекания, а зависит от нач. и конеч. сос-ния с-мы, т.е. определяется физико-химическими св-вами исх. веществ и продуктами. Этот закон действует либо при p=const, либо при V=const.
Закон Гесса утверждает, что тепловой эффект р-ций не зависит от числа стадий и пути протекания стадий, а опред. нач. и конеч. сост. Термохимическими ур-ми называтся такие у-ия в которых указан их тепловой эффект. Q>0(экзо)Q<0(эндо) ΔН(=-Q)зависит от агрегатного сост. в-ва.Энтальпия образования в-ва-тепловой эффект образования одного моля данного в-ва из простых в-в. Стандартной энтальпией образ. в-ва называется тепловой эффект образования 1 моля данного в-ва в стандартных условиях из простых в-в, взятых также в стандартных условиях. Следствия закона Гесса:1)тепловой эффект образования простого в-ва равен 0; 2)тепловой эффект химических реакций равен сумме станд. энтальпий образ. в-ва всех продуктов р-ции минус сумма станд. энт. образ. в-ва всех исходных в-в.(ΔН0=ΣnΔH0прод-ΣnΔH0исх)
|
Основные факторы определяющие скорость гомогенных и гетерогенных реакций. Закон действующих масс. Правило Вант-Гоффа. Важнейшими факторами являются: концентрация, температура, давление. Влияние конц-ции: зависимость скорости р-ции от конц-ции определяется законом действующих масс: скорость р-ции прямопропорциональна произведению конц-ции реагирующих в-в, взятых в степени их коэффициентов. v=k[A]a[B]b, k-константа скорости р-ции, которая зависит от природы реагирующих в-в и от температуры. Для определения k необходимо использовать концентрации в-в равные 1моль/л. Влияние давления: давление и объем косвенно влияют на скорость р-цй - при увеличении давления пропорционально увеличиваются конц-ции в-в и, наоборот, при увеличении объема концентрации уменьшаются. Для р-ций, когда взаимодействует более 3-х молекул, необходимо изучать механизм их протекания, т.е. возможные стадии. Для оценки скорости протекающей р-ции необходимо выявить наиболее замедленную стадию, которая контролирует весь процесс в целом. С учетом возможных стадий процесса различают реакции по их молекулярности и порядку. Влияние температуры: зависимость скорости р-ции от температуры определяется правилом Вант-Гоффа: при повышении температуры на каждые 100 скорость р-ции возрастает в 2-4 раза.
|
Второй закон термодинамики. Энтропия. Вычисление энтропии для химических реакций. Самопроизвольными процессами называют процессы, протекающие без подвода энергии от внешнего источника. Все с-мы разделяются на изолированные, замкнутые и открытые. Изолир.- масса и энергия не изменны.
Замкнутая – масса постоянна, энергия изменяется. Открытая – масса и энергия изменяются. II закон термодинамики – это критерий самопроизвольного протекания р-ций. Для хар-ки микросостояния с-мы используют коородинаты каждой частицы и указывают скорость перемещения каждой молекулы по осям x,y,z. Термодинамич. Вероятностью с-мы называют число микросостояний с помощью которых осуществляется данное макросостояние. W-термодин. вероят. сост. с-мы. W1→W2
По теории Больцмана смешанное низкопорядочное сос-ние является более вероятным, чем раздельное, более упорядоченное. В этом случае происходит переход из менее вероятного сос-ния в более вероятное. Движущей силой самопроизвольного процесса смешения является стремление частиц к хаотическому движению, а сис-мы- к переходу от более упорядоченного к менее упорядоченному сос-нию. Энтропия - термодинамическая функция сос-ния сис-мы, количественно хар-ет меру беспорядка частиц в-ва. S=klnW Энтропия – это величина пропорциональная логарифму числа равновероятных микросост., которыми может быть реализовано данное макросостояние сис-мы, k-постоянная Больцмана. II закон термодинамики: любая изолированная сис-ма предоставленная сама себе изменяется в направлении сос-ния обладающего максимальной термодинамической вероятностью, или в изолированной сис-ме самопроизвольно может протекать только такая реакция, которая сопровождается увеличением энтропии.
ΔS=Sпрод-Sисход; ΔS=0-термодинамическое равновесие;ΔS≥0 – в общем случае для изолированных с-тем.
Электронные структуры атомов элементов малых периодов. Малыми периодами называются периоды с 1-го по 3-ий. Они состоят из одного ряда. Вывод: 1) каждый период начинается с заполнения s-подуровня, а начиная с 3-ей группы p-подуровня. 2) максимальное число электронов на s-подуровне-2, на р-подуровне-6, на всем подуровне-8. 3) валентными электронами являются у s-элементов s-электроны, Ур-элементов- s и р-электроны. 4) у эл-ов 3-го периода остается незаполненным 3d подуровень.
Электронные структуры атомов элементов больших периодов. Большими периодами называются периоды с 4 по 7. они состоят из 2-х рядов. 1) каждый период начинается с заполнения s-подуровня. 2)начиная с 3-ей группы в четных рядах происходит заполнение предыдущего d-подуровня, а начиная с 6-го периода происходит заполнение предыдущего f-подуровня. 3)каждый период заканчивается p-элементами.. 4)валентными являются у s-элементом s-электроны, у р-элементов s и р-электроны, у d-элементов s, p, d-электроны, у f-элементов s, p, d, f-электроны.
Свойства атомов. Радиусы нейтральных атомов и ионов. Изменение их по периодам, группам и подгруппам А и Б. В квантовой химии радиусом называется расстояние от ядра до последнего максимума электронной плотности. Атомные радиусы зависят от заряда и положения атома в периодической сис-ме. Чем больше порядковый номер и чем меньше заряд ядра, тем больше радиус. В главных подгруппах сверху вниз радиусы увеличиваются. В побочных группах сверху вниз радиусы увеличиваются незначительно. Это объясняется тем, что у d-элементов заполняется предвнешние орбитали (эффект экранирования). Слева направо в периодах атомный радиус уменьшается, т.к. увеличивается заряд ядра. У ионов аналогично. У катионов радиусы всегда меньше, чем у нейтральных атомов, у анионов наоборот.
|
Законы термохимии. Их значение. Термохимические расчеты. I закон термохимии (Луавуазье и Лаплас):тепловой эффект образования данного соединения в точности равен, но обратен по знаку тепловому эффекту его разложения. Из закона следует невозможность построения вечного двигателя первого рода, использующего энергию химических реакций. II закон термохимии(Гесс):тепловой эффект хим. р-ции не зависит от хар-ра и последовательности отдельных её стадий а опред. только нач. и конеч. продуктами р-ции и их физич. состоянием.(при p=const или V=const). Закон Гесса позволяет производить точные расчеты тепловых эффектов образования целого ряда в-в, опытные данные о которым было получить трудно.
Принцип Паули и его следствия. Распределение электронов на атомных орбиталях подчиняется принципу Паули: в атоме не может быть двух электронов, у которых были бы одинаковыми все квантовые числа. +/-m=2l+1 В тех случаях, когда l может принимать значение, отличное от 0, появляются подуровни p, d, f. Элементы, которые имеют свободные орбитали, могут переходить в возбужденное состояние, за счет распаривания спаренных электронов и их перехода на свободные орбитали.
|
Константа скорости реакции и её зависимость от температуры. Энергия активации и её графическое определение. Уравнение Аррениуса. Поскольку константа скорости пропорциональна скорости р-ции, поэтому влияние температуры на скорость и константу имеет вид Кt2/Кt1=γt2-t1/10. Более точную функциональную зависимость K(t) установил Аррениус k=Ae–Ea/RT.А -  некоторая постоянная величина, Еа-энергия активации, R-газовая постоянная, Т-темпуратура.
Ln k 1/Т.
Д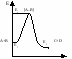 ля образования продуктов р-ции необходимо соблюдение условия соударения молекул. Однако, не всякое соударение приводит к образованию продуктов. Только эффективное соударение приводит к образованию продуктов. Для этого молекулы должны обладать соответствующей энергией. А это значит, что молекулы должны преодолеть некоторый энергетический барьер. [A..B] – состояние активированного комплекса. Чем меньше энергия активации, тем легче протекает реакция, с большей скоростью.
|
Понятие об энтропии. Абсолютная энтропия веществ. Третий закон термодинамики. Наименьшим значение энтропии обладают в-ва с кристаллическим строением. Вывод: энтропия возрастет во всех процессах сопровождающееся усилением беспорядочного движения частиц в-ва и уменьшением порядка в относительном расположении частиц. Во всех процессах , в которых упорядоченность мы возрастает сопровождающихся уменьшением числа частиц, особенно в газообразном состоянии ΔS<0. III закон термодинамики: при абсолютном нуле энтропия кристалла равна нулю.
|
Химическое равновесие. Принцип Ле Шателье и его следствия. Значение этого принципа для интенсификации производственных процессов. Большинство химических реакций, т.е протекают одновременно в прямом и обратном направлениях. В тех случаях, когда прямая и обратная р-ции идут с одинаковой скоростью, наступает химическое равновесие. Химические р-ции в гетерогенной среде протекают на границе раздела между всеми фазами. Состояние хим. равновесия может сохраняться при данных неизменных условиях достаточно длительное время. При зименении условий состояние равновесия нарушается. Принцип Ле Шателье: если на физико-химическую с-му, находящуюся в равновесии, оказывают внешнее воздействие, то оно смещается в направлении того процесса, протекание которого ослабляет внешнее воздействие.
|
Энергия Гиббса и ее применение при химических процессах. Стандартная энергия Гиббса. Направленность химических процессов. Направление в котором самопроизвольно протекает хим. р-ция определяется совместным действием двух факторов: стремление с-мы перейти в состояние с наименьшей энергией (ΔН<0); стремление с-мы перейти в состояние с максимально возможным молекулярным беспорядком (ΔS>0). Суммарный эффект этих двух противоположных тенденций отражает изменение энергии Гиббса. ΔG=ΔH-TΔS для рТ=const. Энергия Гиббса характеризует ту часть полной энергии с-мы, которая может быть превращена в работу при рТ=const: 1)ΔG<0-условие самопроизвольности протекания процесса в прямом направлении при заданных р и Т. ΔGпрод<ΔGисх 2)ΔG=0-предел самопроизвольного протекания процесса; ΔG>0-процесс не возможен в прямом направлении при заданных условиях(ΔGпрод>ΔGисх). Энергией Гиббса образования химического соединения называют изменение энергии Гиббса в реакции образования 1 моля хим. соединения из простых в-в при стандартных условиях. При ΔH<0,ΔS>0,ΔG<0 возможно протекание самопроизвольного процесса при любых Т; ΔH>0,ΔS<0,ΔG>0 не возможно протекание самопроизвольного процесса ни при каких Т; ΔH<0,ΔS<0,ΔG<0 возможно протекание самопроизвольного процесса при низких Т;ΔH>0,ΔS>0,ΔG<0 возможно протекание самопроизвольного процесса при высоких Т.
|
Химическое равновесие. Константа равновесия в гомогенных и гетерогенных реакциях. Константа хим. равновесия зависит от природы реагирующих в-в и от температуры и не зависит от давления и концентрации реагентов. Если в гетерогенной р-ции участвуют твёрдые и газообразные в-ва, то в выражение для константы хим. равновесия входят только парциальные давления газообразных компонентов р-ции. Константа равновесия может быть выражена через молярные доли. Однако она допустима лишь для достаточно разряженных с-м, в которых влияние межмолекулярных сил на активность компонентов очень мало. Константа равновесия может быть выражена через парциальные давления: Кр=pАВ/рАрВ, где pАВ, рА, рВ –парциальные давления реагирующих газов в равновесной с-ме. Парциальное давление равно pi=p0Ni, где p0-общее давление газовой смеси. Кр имеет размерность давления и равна Кр=Kfp0Σn, где Σn –сумма коэффициентов р-ции, в которой коэффициенты продуктов идут со знаком плюс, а начальных продуктов-с минусом. Константа равновесия может быть выражена через молярные концентрации С(моль/л). Такой способ удобен для р-ций , идущих при V=const. КC=CАВ/САСВ (размерность концентрации). КС=КР(RT)-Σn, где Σn- сумма коэффициентов продуктов реакции. Если р-ция идет без изменении числа молей и Σn=0, то все выражения констант равновесия будут совпадать, и они будут безразмерные. Константа равновесия для гетерогенной обратимой р-ции KP=pгаза/жидкости=f(T). Выбор параметров, влияющих на равновесие в гетерогенной с-ме, и условия равновесия определяются правилом фаз Гиббса-Коновалова: число степеней свободы в гетерогенной с-ме равно числу компонентов плюс 2 и минус число фаз.
| |
Скачать 206.5 Kb.