ПРимеры практических. 1,2 Очники Примеры практ.. "Гидростатическое давление в жидкости"
 Скачать 2.89 Mb. Скачать 2.89 Mb.
|
Примеры решения задач по теме:“Расчёт сложных трубопроводных систем”Задача 20. Сложная система с водонапорной башней включает кольцевое соединение труб и доставляет воду двум потребителям (рис. 24). Определить отметку уровня воды в водонапорной башне, питающей два потребителя: « А» с расходом QA = 18 л/c и «С» с расходом QC = 32 л/c. Система включает магистральный трубопровод с параметрами d1 = 250 мм, l1 = 600 м; два параллельно проложенных трубопровода с параметрами d2 = 150 мм, l2 = 550 м, d3 = 100 мм, l3 = 400 м и трубопровод d4 = 200 мм, l4 = 720 м, подающий воду потребителю С. Остаточный напор у потребителя С должен быть не менее 10 м; Местные потери напора принять равными 10 % от потерь по длине. Построить пьезометрическую линию. Решение. Руководствуемся методикой расчёта сложных систем с параллельным соединением труб. 1. Распределение расхода (пропускной способности). На каждом участке вводим обозначение расхода с индексом, соответствующим индексу диаметра трубы (рис. 24). Расход на первом участке равен сумме расходов потребителей: Q1 = QA +QC ; Q1 = 50 л/с = 0,05 м3/с. Сумма расходов в параллельных трубопроводах равна расходу потребителя С:Q2 + Q3 = QC ; Q2 +Q3 = 32 л/с = 0,032 м3/с. Пропускная способность четвёртого участка равна расходу потребителя С: Q4 = 0,032 м3/с. 2. Приравняем потери напора по длине в параллельных трубопроводах кольца, чтобы найти распределение расхода в параллельных участках: с учётом формулы: 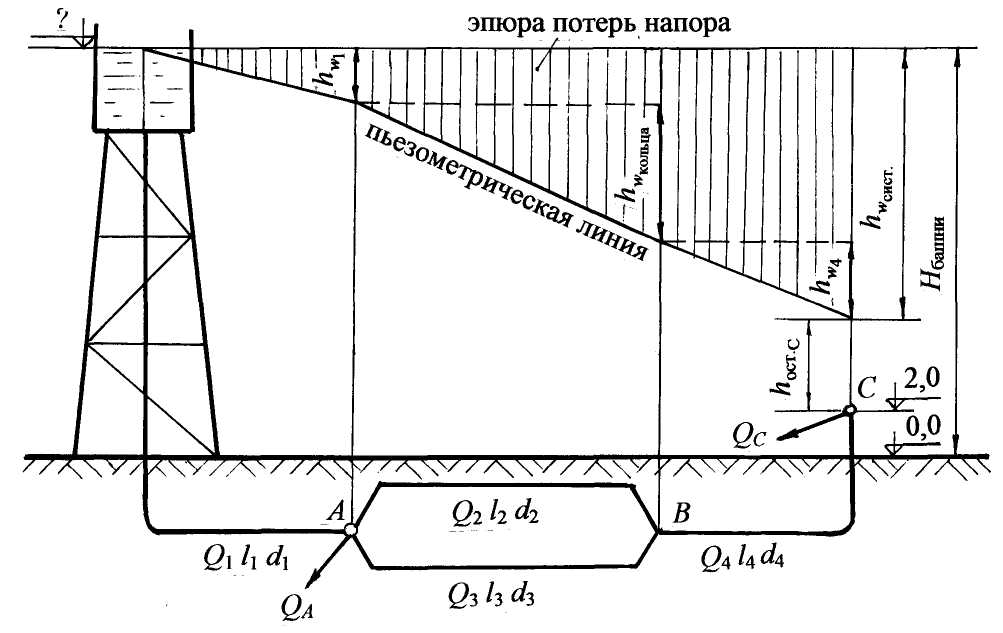 Рис. 24 Выразим Q3 через Q2: Согласно табл. 8 (приложение), для: d2 = 150 мм удельное сопротивление А2 = 31,18 с2/м6; d3 = 100 мм удельное сопротивление А3 =265 с2/м6, тогда Подставим значение Q3, выраженное через Q2, в формулу: Q2 + 0,4 Q2 = 0,032 м3/с, отсюда Q2 = 0,023 м3/c; значит, Q3 = 0,009 м3/c. 3. Геодезическая высота, или отметка уровня воды в водонапорной башне относительно нулевой отметки (рис. 24): Объясним эту формулу для высоты водонапорной башни: отметка воды в водонапорной башне должна быть такой, чтобы поднять воду у потребителя С на высоту 2,0 м, обеспечить остаточный напор не менее 10 м и преодолеть гидравлические сопротивления в системе. 1Рассчитаем потери напора (гидравлические сопротивления) в системе: где 1,1 – поправочный коэффициент на местные сопротивления, т.к. по условию задачи потери напора в местных сопротивлениях составляют 10 % от потерь по длине; Потери напора в системе с учётом формулы (2.42): Рассчитаем потери напора в системе, принимая: А1 = 2,11 с2/м6 для диаметра d1 = 250 мм; А4 = 6,78 с2/м6 для d4 = 200 мм по табл. 8 (приложение): = 3,5 + 10,0 + 5,5 = 19,0 м. Для построения пьезометрической линии учтем потери напора на каждом участке: На рис. 24 откладываем в масштабе потери напора на каждом участке и строим пьезометрическую (напорную) линию. Находим отметку уровня воды в водонапорной башне: Нбашни = 2,0 + 19,0 + 10,0 = 31,0 м. Ответ: отметка уровня воды в водонапорной башне должна быть не менее 31,0 м. Задача 21 Тупиковая водопроводная система имеет пять участков труб, у которых длины и диаметры указаны на рис. 3.15. В системе четыре потребителя с расходами: QA = 10 л/c; QB = 18 л/с; QC = 12 л/c; QD = 8 л/c; на пятом участке равномерная раздача воды с путевым расходом Qпут = 15 л/c. Определить высоту водонапорной башни Н, рассчитать диаметры труб на первом и третьем участках системы при условии, что эксплуатационная скорость υэкс Принять l1 = 500 м; l3 = 450 м; d2 = 150 мм; l2 = 550 м; d4 = 125 мм; l4 = 600 м; d5 = 150 мм; l5 = 700 м. Потери напора в местных сопротивлениях составляют 5 % от потерь по длине. Построить пьезометрическую линию. Решение. Воспользуемся методикой расчёта тупиковых систем и систем с путевым расходом (разделы 3.1.9 и 3.1.10). 1. Обозначимна схеме расходы на каждом участке с соответствующими индексами, найдём их значение и переведем л/с в м3/c (рис. 3.15). Первый участок является магистральным для всех потребителей: Q1 = QA + QB + QC + QD + Qпут = 0,063 м3/с. Третий участок магистральный для потребителей CиD и путевого расхода: Q3 = QC + QD + Qпут = 0,035 м3/с. Для второго и четвёртого участков: Q2 = QB = 0,018 м3/c; Q4 = QC = 0,012 м3/c. 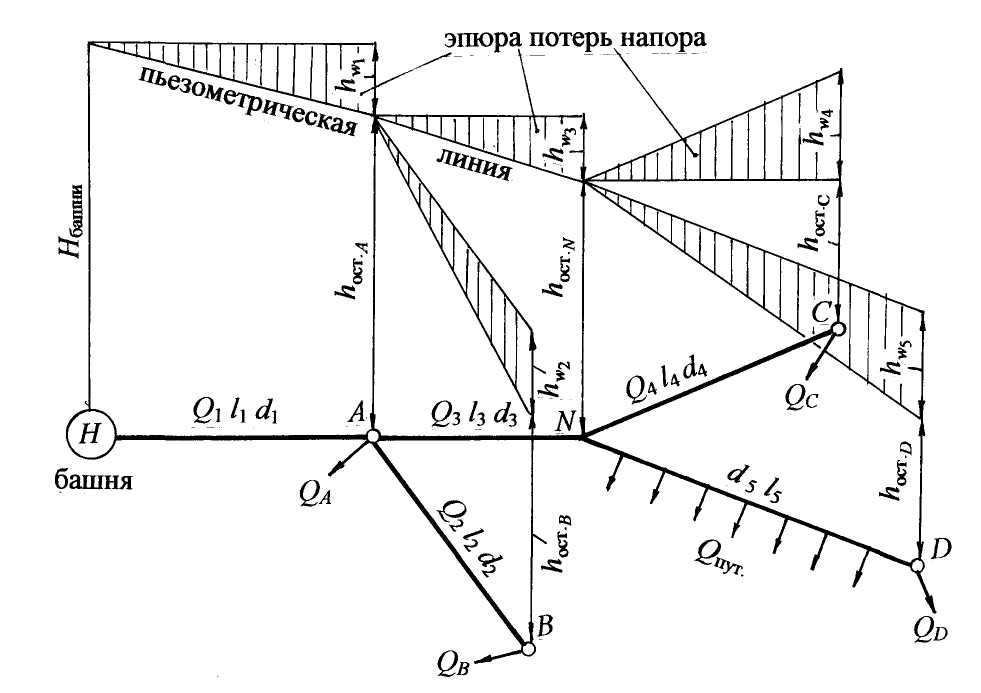 Рис. 3.15 2. Рассчитаем диаметры труб на первом и третьем участках по формуле (3.43): Получим: принимаем d1 = 250 мм; принимаем d3 = 200 мм. 3. Определим потери напора на участках 1–4 с учётом местных сопротивлений по формуле: hw = 1,05 hl = 1,05 AQ2l. Для всех диаметров труб, указанных в условии задачи, выбираем значения коэффициентов удельного сопротивления по табл. 8 (приложение): А1 = 2,11 с2/м6; А2 = 31,18 с2/м6; А3 = 6,78 с2/м6; А4 = 81,6 с2/м6; А5 = 31,18 с2/м6. Получим по аналогии: Потери напора на пятом участке с учётом путевого расхода Qпут и транзитного расхода в виде расхода потребителя D (QD), согласно формуле (3.44) равны: после подстановки численных значений: Рассчитаем потери напора по трём направлениям к потребителям В, С, D, принимая последовательное соединение труб: 4. По формуле (3.42) определим высоту водонапорной башни: В данной задаче остаточный напор у всех конечных потребителей принимаем равным 10 м, поэтому, сравнивая потери напора по всем направлениям, выбираем максимальные, которыми являются потери напора до потребителя С: Таким образом, высота водонапорной башни равна: 5. Строим пьезометрическую линию. Для первого и третьего участков пьезометрическую линию построим в вертикальной плоскости, для других участков пьезометрическую линию представим в изометрии путём параллельного переноса направления трубопровода (рис. 3.15). Построение можно упростить. Чтобы на чертеже не было наложения эпюр потерь напора, можно от остаточного напора в точках A иNоткладывать потери напора на участках втором, четвёртом и пятом, как представлено на рис. 3.15. Из построения пьезометрической линии следует, что остаточные напоры у всех потребителей, кроме потребителя С, больше 10,0 м. Вертикальной штриховкой показана эпюра потерь напора. В примерах решения задач 3.1.11.1 и 3.1.11.2 расчёты сложных систем проведены без составления уравнения Бернулли, т.к. эти расчёты аналогичны расчётам простых систем (раздел 3.2). На примере решения задачи 3.1.11.3 представим расчёт сложной системы путём составления уравнения Бернулли. Задача 22 Из водонапорной башни А, в которой на поверхности воды действует избыточное давление рман, по трём последовательно соединённым трубам подаётся вода для трёх потребителей с расходами: QB = 15 л/с; QC = 8 л/c; QD = 12 л/c. Диаметры и длины участков системы принять: d1 = 200 мм, l1 = 700 м; d2 = 150 мм, l2 = 600 м; d3 = 125 мм, l3 = 500 м. Остаточный (свободный) напор у потребителя D должен быть не менее 10 м ( Н = 15 м считать постоянным (рис. 3.16). Определить, каким должно быть показание манометра рман на поверхности воды в башне для обеспечения водой потребителей при условии, что местные сопротивления составляют 10 % от потерь по длине. Водопроводные трубы нормальные. Построить пьезометрическую линию. Решение. Для расчёта системы (рис. 3.16) воспользуемся уравнением Бернулли по принятой методике (раздел 2.1.12). 1. Выбираем два сечения по свободной поверхности воды в башне: одно сечение – где скорость воды можно считать равной нулю, другое сечение у потребителя D. 2. Сечения нумеруем по направлению движения воды: 1–1 по свободной поверхности воды, где действует манометрическое давление; 2–2 по трубопроводу у потребителя D. 3. В выбранных сечениях учитываем абсолютное давление: р1 = ра + рман; р2 = ра + ρg 4. Плоскость сравнения0–0 совместим с сечением2–2, тогда z1 = H; z2 = 0. 5. Записываем уравнение Бернулли в общем виде и производим подстановку параметров: z1 = H; z2 = 0; p1 =pа + рман; р2 = ра + ρg υ1 = 0; υ2 = υ; α2 = 1,0; После подстановки параметров получим: Как указано в разделе 3.3, скоростным напором Поясним уравнение (3.46): за счёт избыточного напора на поверхности воды в башне и действующего напора происходит преодоление всех сопротивлений в системе и обеспечение остаточного напора у потребителя. 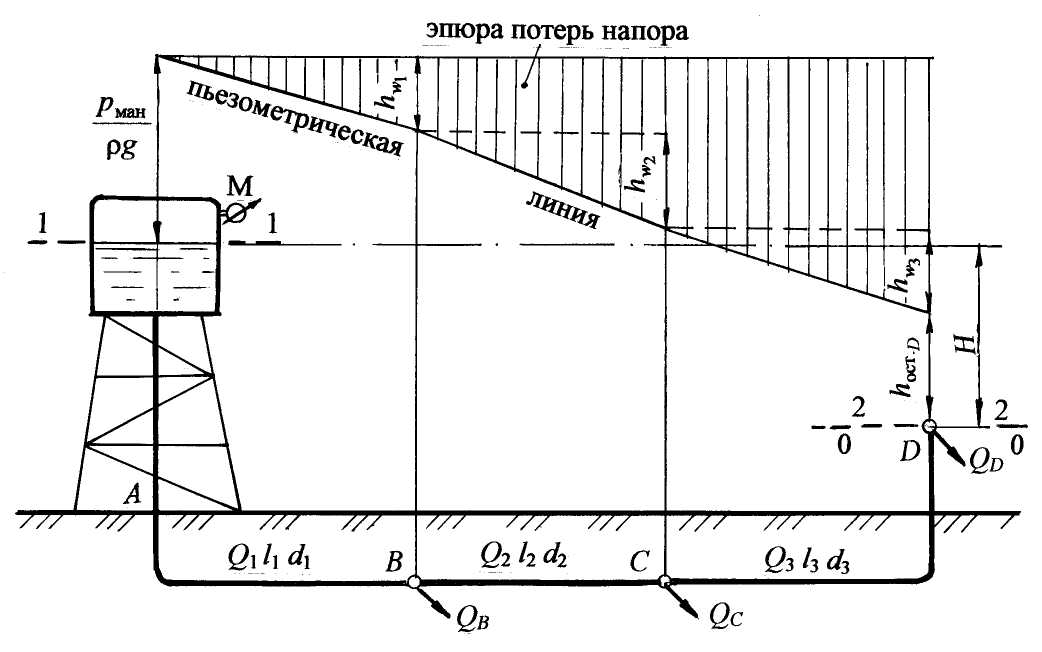 Рис. 3.16 Чтобы рассчитать показание манометра рман в формуле (3.46), следует определить потери напора в системе Воспользуемся методикой расчёта сложных систем (раздел 3.3). 1. Распределение расхода. На каждом участке вводим обозначение расхода с индексом, соответствующим индексу диаметра трубы: Q1;Q2;Q3. Рассчитаем расход на каждом участке через расходы потребителей: Q1 = QB + QC + QD; Q1 = 35 л/c = 0,035 м3/c; Q2 = QC + QD; Q2 = 20 л/c = 0,020 м3/c; Q3 = QD; Q3 = 12 л/c = 0,012 м3/c. 2. Определим потери напора в системе При последовательном соединении труб потери напора на всех участках суммируются (раздел 3.1.7). С учётом поправочного коэффициента на местные сопротивления получим: затем с учётом формулы (2.42): Рассчитаем потери напора в системе, принимая следующие коэффициенты удельных сопротивлений (приложение, табл. 8) для соответствующих диаметров d1, d2, d3, указанных в условии задачи: А1 = 6,78 с2/м6; А2 = 31,18 с2/м6; А3 = 81,60 с2/м6 . Для построения пьезометрической (напорной) линии нужно знать потери напора на каждом участке трубопровода, поэтому формулу (3.47) представим в виде трёх слагаемых: 3. Обратимся к формуле (3.46) для определения показания манометра рман на поверхности воды в водонапорной башне: отсюда рман = 16,1ρg, рман = 16,1·103·9,8 = 157·103 Па = 157 кПа. Показание манометра можно представить в атмосферах, помня, что 1ат = 10м вод.ст. Тогда Ответ: показание манометра рман = 157 кПа или рман = 1,61 ат. В задачах 3.1.11.1; 3.1.11.2; 3.1.11.3 при расчёте сложных систем необходимо было определить уровень воды в водонапорной башне, высоту водонапорной башни, показание манометра на поверхности воды в водонапорной башне, т.е. определить параметры, связанные с давлением или напором. В задаче 3.1.11.4 предлагается определить: расход воды (т.е. пропускную способность) в магистральном трубопроводе, распределение расхода в параллельных участках трубопроводной системы, а также показания манометров в определённых точках системы. Задача 23 Из водонапорной башни А с отметкой горизонта НА= 24,0 м вода подаётся в напорный бак В с отметкой горизонта воды НВ = 12,0 м. Система трубопроводов имеет закольцованный участок CD. В узлах разветвления C и D выведены манометры М1 и М2 (рис. 3.17). Диаметры и длины участков трубопроводов: d1 = 250 мм, l1 = 600 м; d2 = 150 мм, l2 = 400 м; d3 = 125 мм, l3 = 360 м; d4 = 200 мм, l4 = 500 м. Трубы проложены на одном горизонте. Определить расход воды в системе Q= Q1, а также распределение расхода воды в параллельных участках Q2 иQ3. Рассчитать показания манометров Потери напора в местных сопротивлениях составляют 10 % от потерь напора по длине. 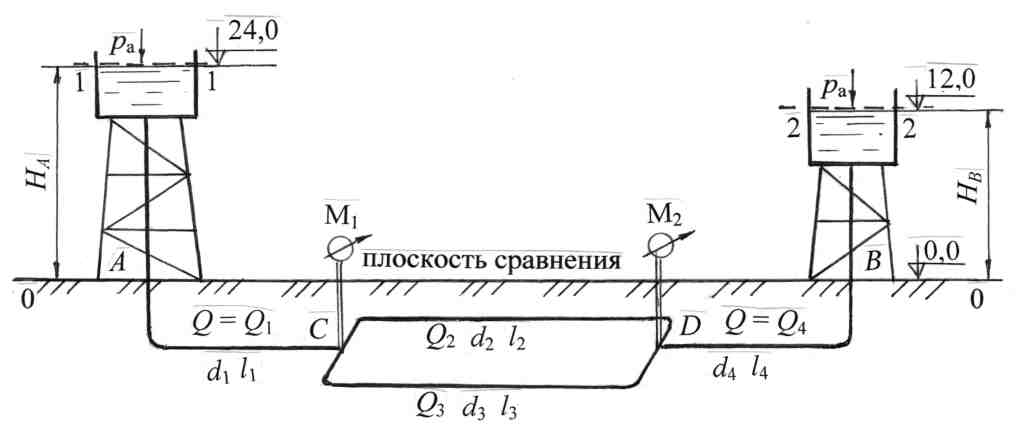 Рис. 3.17 Для расчёта данной системы воспользуемся уравнением Бернулли (2.15) по принятой методике. Выбираем два сечения: одно по свободной поверхности в напорной башне А, второе – по свободной поверхности в напорном баке В. Сечения нумеруем по направлению движения воды: 1–1 и 2 – 2. В выбранных сечениях учитываем абсолютное давление, равное атмосферному давлению, т.к. резервуары открыты: р1 = ра; р2 = ра. Скорости в выбранных сечениях, т.е. на свободной поверхности, равны нулю: υ1 = υ2 = 0. Плоскость сравнения 0 – 0 совместим с нулевой отметкой. 5. Записываем уравнение Бернулли в общем виде и подставляем параметры: z1 = НА, z2 = НВ, p1 = pа , р2 = ра , υ1 = υ2 = 0, После преобразований получим: НА – НВ = Формула (3.48) аналогична формуле (3.6) расчёта простой системы при истечении под уровень: действующий напор затрачивается на преодоление гидравлических сопротивлений в системе Проводим расчёт системы, согласно принятой методике (раздел 3.3): 1. Распределение расхода. Обозначим расход на каждом участке с индексом, соответствующим индексу диаметра: Q1, Q2, Q3, Q4. В трубопроводной системе отсутствуют промежуточные потребители, значит, расходы на первом и четвёртом участках как магистральных равны общему расходу в системе: Q = Q1; Q = Q4. 2. Потери напора в системе из потерь напора на первом участке 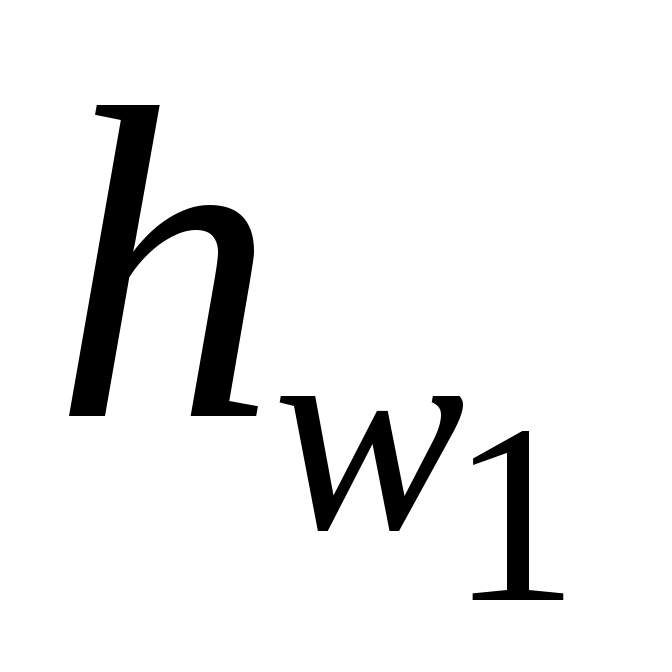 ; в кольце ( ; в кольце (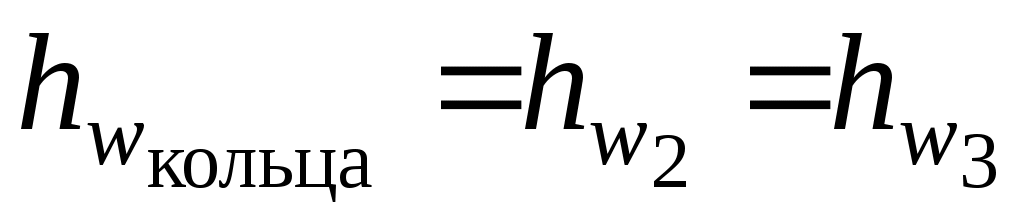 ), согласно формуле (3.32) и на четвёртом участке ), согласно формуле (3.32) и на четвёртом участке 3. Выразим расходыQ2 и Q3 через общий расходQ в системе: Q = Q2 + Q3 . (3.50) Приравняем потери по длинена втором и третьем участках трубопроводов, согласно формуле (3.33): т.е. в соответствии с формулой (2.42) имеем: А2 где А2 и А3 – коэффициенты удельного сопротивления: А2 = 31,18 с2/м6 для d2 = 150 мм; А3 = 81,6 с2/м6 для d3 = 125 мм (приложение, табл. 8). Выразим расход Q3 через расход Q2: Полученный расход Q3 подставим в формулу (3.50): Q = Q2 + 0,652 Q2 = 1,652 Q2, отсюда Q2 = 0,605Q . 4. Определим потери напора в системе Введём поправочный коэффициент на местные сопротивления, равный 1,1 (местные сопротивления составляют 10 % от потерь по длине), формула (3.26): Потери напора по длине в кольце приравняем к потерям напора на втором участке: Учтем в расчётах расход на каждом участке (формула 2.42): =1,1 Q2( A1l1 + 0,366 A2l2 + A4l4). Значение коэффициентов А1 и А4 принимаем по табл. 8 (приложение): А1 = 2,11 с2/м6 для d1 = 250 мм; А4 = 6,78 с2/м6 для d4 = 200 мм, тогда Из формулы (3.48) определим потери напора в системе Рассчитываем общий расход в системе: Q = Расходы на втором и третьем участках системы равны: Q2 = 0,605Q = 20,8 л/с; Q3 = 0,652Q2 = 13,6 л/с. Проверим: Q2 + Q3 = Q; 20,8 + 13,6 = 34,4 л/с. Расчёты верны. Рассчитаем потери напора на каждом участке трубопроводной системы: Проверка: Расчёты расходов и потерь напора на всех участках системы верны. 5. Определим показание первого манометра Воспользуемся логическими рассуждениями, т.е.: напор в месте установки первого манометра равен разности напоров в водонапорной башне и потерь напора на первом участке: Напор в месте установки второго манометра должен быть таким, чтобы преодолеть гидравлические сопротивления на четвёртом участке и поднять воду в напорный бак на высоту НВ: Можно сделать ещё одну проверку: разность напоров в местах установки первого и второго манометров равна потерям напора в кольце, т.е. действительно, Проведены все проверки. Расчёты верны. Ответ: расход воды в системе Q = 34,4 л/с; расход на втором участке Q2 = 20,8 л/с; расход на третьем участке Q3 = 13,6 л/с; показание первого манометра показание второго манометра |
