ПРимеры практических. 1,2 Очники Примеры практ.. "Гидростатическое давление в жидкости"

• Название: "Гидростатическое давление в жидкости"
• Анкор: ПРимеры практических
• Дата: 07.05.2022
• Размер: 2.89 Mb.
• Имя файла: 1,2 Очники Примеры практ..doc
• Тип: Задача; #516168
• страница: 1 из 8

Примеры решения задач по теме:

“Гидростатическое давление в жидкости”

При решении задач по определению давления в покоящейся жидкости следует пользоваться следующей методикой.

1. Выбрать плоскость уровня 0 – 0 (плоскость равного давления), для которой давление в любой точке плоскости имеет постоянную величину, т.е.

р = const.

Такой плоскостью является горизонтальная плоскость в однородной покоящейся жидкости, находящейся в поле действия только сил тяжести.

Возможно, для решения задачи потребуется провести не одну, а две плоскости.

2. Пронумеровать плоскости уровня и составить условия равенства давления для выбранных плоскостей. Записать выражения для давлений в соответствии с основным уравнением гидростатики.

3. Решить совместно полученные выражения для определения необхо-димых параметров. Все расчёты вести в системе СИ.

Задача 1.

К закрытому резервуару (рис. 1), заполненному водой, на глубине

h =1,0 м подсоединён чашечный ртутный манометр. Понижение уровня ртути в чашке прибора, называемое поправкой прибора, равно а= 100 мм.

Показание чашечного манометра h_рт = 120 мм. Над ртутью налито масло, высота уровня масла h_м = 80 мм, плотность масла ρ_масл = 900 кг/м³.

Определить абсолютное давление на поверхности воды в резервуаре р_абс, а также указать, каким прибором следует измерять величину давления на поверхности воды. Принять плотность воды ρ = 10³ кг/м³; плотность ртути ρ_рт = 13,6·10³ кг/м³; атмосферное давление р_а = 730 мм рт. ст.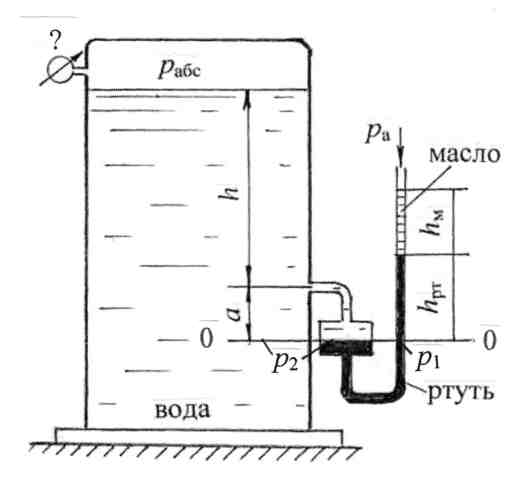




Рис. 1

Решение.
Решение ведём с учётом атмосферного давления, т.к. по условию задачи требуется определить абсолютное давление воды на поверхности в резервуаре.

Согласно методике по определению давления в жидкости, восполь-зуемся понятием плоскости уровня.

Выберем плоскость уровня 0–0 на разделе жидкостей «вода – ртуть». Плоскость уровня 0–0 пройдёт по ртутному прибору и может быть продолжена в резервуаре с водой.

Составим условие равенства давления, приравняв давления в правом р₁ и левом колене р₂ чашечного ртутного манометра:

p₁ = p₂;

p₁ =p_a + ρ_маслgh_м + ρ_ртgh_рт;

p₂ = p_абс + ρg(h +a).

Приравняем давление в правом и левом колене чашечного ртутного манометра: p_a + ρ_маслgh_м + ρ_ртgh_рт = р_абс +ρg(h +a),

отсюда абсолютное давление на поверхности воды в резервуаре:

р_абс = р_а + ρ_маслgh_м + ρ_ртgh_рт – ρg(h + a).

Рассчитаем атмосферное давление в системе СИ:

р_а = 730 мм рт. ст. = 730·133,3 = 97309 Па.

Абсолютное давление на поверхности воды в резервуаре:

р_абс = 97309 + 900·9,8·0,08 +13,6·10³·9,8·0,12 -10³·9,8·1,1 =103228 Па;

р_абс > р_а, значит давление на поверхности воды избыточное, или манометрическое: р_ман = р_абс – р_а = 103,2 – 97,3 = 5,9 кПа,
Ответ: р_абс = 103,2 кПа. Показание манометра на поверхности воды р_ман = 5,9 кПа или в технических атмосферах р_ман = 0,06 ат.
Задача 2.
К резервуару (рис. 2), заполненному бензином плотность которого равна ρ_бенз.= 700 кг/м³, присоединён U–образный ртутный манометр, показание которого h_рт = 0,1 м; уровень масла над ртутью h_м = 0,2 м.

Определить абсолютное давление паров на поверхности бензина р_абс и показание пружинного манометра р_ман, установленного на крышке резервуара, а также возможную высоту уровня бензина h_p в пьезометре, выведенном на глубине H = 1,1м, при условии, что h= 0,75 м; а = 0,15 м.

Принять плотность ртути ρ_рт = 13,6·10³ кг/м³; плотность масла

ρ_масл = 820 кг/м³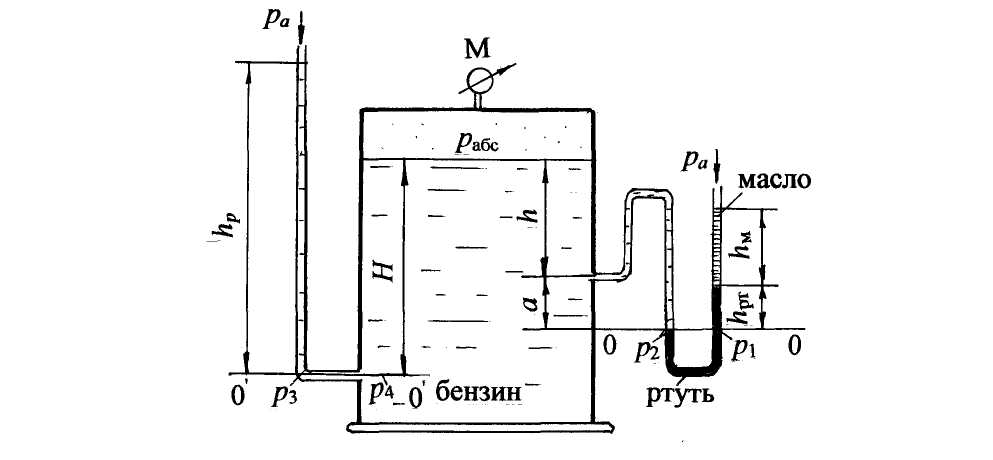


Рис. 2

.
Решение.
Решение ведём с учётом атмосферного давления, т.к. по условию задачи требуется определить абсолютное давление паров бензина.

Для решения задачи выберем плоскость уровня 0–0 на разделе жидкостей «бензин–ртуть» и составим условие равенства давления, приравняв давления в правом (р₁₎ и левом колене (р₂₎U–образного манометра: p₁ = p₂;

p₁ =p_a + ρ_маслgh_м + ρ_ртgh_рт;

p₂ = p_абс + ρ_бензg(h +a).

Приравняем давление в правом и левом колене U–образного манометра:

p_a + ρ_маслgh_м + ρ_ртgh_рт = р_абс +ρ_бензg(h +a),

отсюда абсолютное давление паров бензина равно:

р_абс = р_а + ρ_маслgh_м + ρ_ртgh_рт – ρ_бензg(h + a).

Принимая атмосферное давление p_a = 98·10³ Па = 98 кПа, получим:

p_абс= 98·10³ + 820·9,8·0,2 +13,6·10³·9,8·0,1 – 700·9,8·0,9 = 106,76 ·10³ Па.

Показание манометра, установленного на крышке бака, можно определить так:

р_ман = р_абс – р_а = ρ_маслgh_м + ρ_ртgh_рт – ρ_бензg(h +a) = 8,76 кПа = 0,089 ат.

Для определения возможной высоты бензина в пьезометрической трубке h_p составим условие равновесия жидкости относительно плоскости уровня 0^'–0^', в этом случае расчёты можно вести по избыточному (манометрическому) давлению. Для плоскости уровня 0^'–0^' запишем равенство давлений: р₃ = р₄:

ρ_бензgh_p = p_ман + ρ_бензgH,

отсюда = 2,38 м.

Ответ: р_абс = 106,76 · 10³ Па = 106,76 кПа; p_ман = 8,76 кПа; h_p = 2,38 м.

Задача 3.

Определить показание U–образного ртутного манометра h_рт ( рис. 3), подключённого к закрытому резервуару с бензином. На поверхности бензина действует давление р₀. Уровень ртути находится на расстоянии h₁ = 1,0 м от свободной поверхности. На глубине h = 1,5 м установлен вакуумметр, показание которого р_вак = 49,8 кПа.

Вакуумметр на рис 3 обозначен буквой В.

Принять плотности жидкостей: бензина r_бенз = 720 кг/м³; ртути

ρ_рт = 13,6·10³ кг/м³.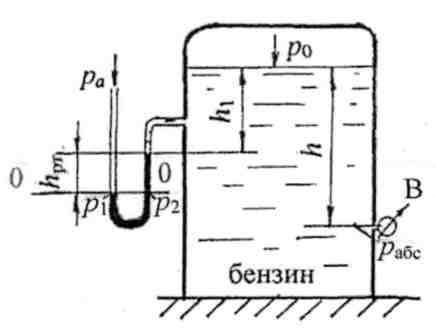




Рис. 3
Решение.
При решении задачи следует помнить, что вакуумметрическим называется давление,недостающее до атмосферного, и при расчётах это давление принимается со знаком минус.

В месте установки вакуумметра абсолютное давление равно:

р_абс = р_а – р_вак.

Расчёты можно провести без определения р₀.

С одной стороны, проведем плоскость уровня 0–0 по U–образному манометру, для которой р₁ = р₂; р₁ = р_а;

р₂ = р₀ + ρ_бензgh₁ + ρ_ртgh_рт;

отсюда р₀ = р_а – ρ_бензgh₁ – ρ_ртgh_рт.
С другой стороны,

р₀ = р_абс – ρ_бензgh = р_а – р_вак – ρ_бензgh.

Приравняем выражения для р₀, сократим р_а, получим:

ρ_бензgh₁ + ρ_ртgh_рт = р_вак + ρ_бензgh,

отсюда ;

.

Ответ: показание U–образного ртутного манометра равно: h_рт= 0,4 м.

Задача 4.
Два резервуара А и В, линии центров которых находятся на одном горизонте, заполненные водой и бензином, соединяются двухколенным ртутным манометром (рис. 4). Пространство между уровнями ртути в манометре заполнено маслом плотностью ρ_масл = 900 кг/м³.

Определить, в каком резервуаре на уровне оси давление больше и на какую величину, если высоты уровней жидкостей соответственно равны:

h₁ = 250 мм; h₂ = 120 мм; h₃ = 80 мм; h₄ = 50 мм.

Принять плотность бензина ρ_бенз =720 кг/м³, ртути ρ_рт=13,6×10³ кг/м³.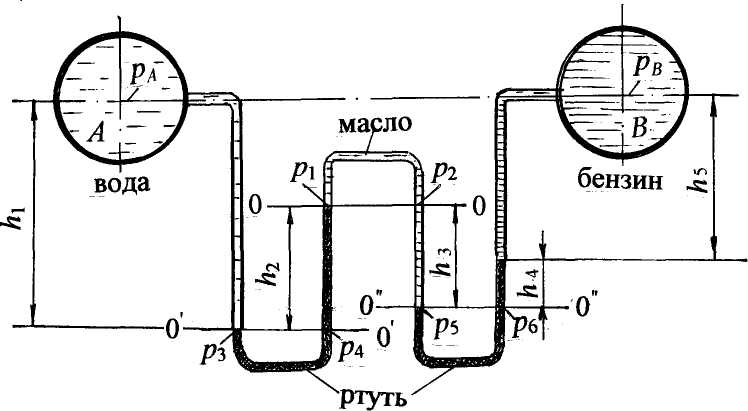





Рис. 4


Решение.
Резервуары закрыты, поэтому давление будем рассчитывать по избыточному давлению без учёта атмосферного давления. Обозначим давление на уровне центра в левом резервуаре р_А , в правом – р_В.

Покажем положение плоскостей уровня для данной равновесной системы: это плоскости 0–0; 0^'–0^'и0^"–0^".

Эти горизонтальные плоскости проводятся по однородной жидкости: плоскость 0–0 по маслу, две другие по ртути. Для этих плоскостей запишем условие равенства давлений:

p₁ =p₂; p₃ =p₄;p₅ =p₆.

Плоскость 0–0 является основной плоскостью равновесного состояния, для которой: р₁= р₂ .

Согласно основному уравнению гидростатики, чтобы определить давление р₁, нужно к давлению в центре резервуара А (р_А) прибавить давление столба воды ρgh₁, в результате получим давление р₃ = р₄.

Если из давления р₄ вычесть давление столба ртути ρ_ртgh_2, в результате получим давление р₁:

p₁ = p_A + ρgh₁ – ρ_рт gh₂.

Аналогично определим давление р₂:

Для этого к давлению в центре резервуара В (р_В) прибавим давление столба бензина ρ_бензgh₅ и давление столба ртути ρ_ртgh₄ , в результате получим давление р₆= р₅.

Затем от плоскости 0^"– 0^" поднимемся вверх до плоскости 0–0, т.е. вычтем давление столба масла ρ_масл gh₃ и получим давление р₂:

р₂ = р_В +ρ_бензgh₅ + ρ_ртgh₄ – ρ_маслgh₃.

В соответствии с рисунком высота столба бензина равна

h₅ = h₁ – h₂ + h₃ – h₄ = 160 мм.

По распределению уровня ртути в дифференциальном манометре предполагаем, что давление по центру резервуара А больше, чем давление в центре резервуара В.

Определим эту разность:

Δp = p_A– p_B= ρ_бенз gh₅ + ρ_рт gh₄ – ρ_мас gh₃ – ρgh₁ + ρ_рт gh₂

При подстановке численных значений следует перевести высоты уровней жидкости в метры.
Ответ: Δp = p_A–p_B =20,63 кПа. Т.к. ответ получился положительным, следовательно, давление в резервуаре Абольше.


Задача 5.
Определить, какое давление – манометрическое р_мв или вакуумное показывает мановакуумметр МВ (рис. 5), установленный по оси резервуара В с керосином, если показание манометра по центру резервуара Ас водой р_ман =0,12 ат. Между резервуарами подключён U–образный ртутный манометр, показание которого h_рт=200 мм; расстояние от уровня ртути в левом колене до оси резервуара А равно h = 300 мм.

Оси центров резервуаров находятся на одной линии.

Принять плотность керосина равной: ρ_кер = 820 кг/м³; ртути равной

ρ_рт = 13,6·10³ кг/м³.


Рис. 5
Примечание. Мановакуумметр – это прибор для измерения как манометрического, так и вакуумметрического давления, имеющий шкалу

измерения со знаком «+» (манометрическое давление) и со знаком «–» (вакуумметрическое давление).

Решение.
В предыдущих задачах подробно изложена методика определения давления путём составления условия равенства давления относительно плоскости уровня.

Выводы из этих задач:

Во-первых, по плоскости уровня можно перейти в любую точку однородной жидкости и давление не изменится.

Во-вторых, при расчёте весового давления жидкости ρgh, в случае увеличения глубины (отсчёты вниз), давление увеличивается и учитывается со знаком «+», в случае уменьшения глубины (поднимаемся вверх) давление уменьшается и учитывается со знаком «–».

В данной задаче (рис. 5) основной плоскостью уровня для всей системы является плоскость 0–0, которая в левой части проходит по уровню воды, в правой – по уровню ртути U образного манометра.

Для этой плоскости имеем р₁ = р₂ = р₃.

В другой плоскости 0^'–0^', проведённой в керосине, имеем р₄ = р₅. Задачу будем решать без учёта атмосферного давления.

Значит, если рассчитанное давление на уровне установки мановакуумметра МВ получится положительным, прибор работает как манометр, если давление получится отрицательным, т.е. вакуумметрическим, прибор работает как вакуумметр.

Запишем давление на уровне установки мановакуумметра путем следующих рассуждений.

Пусть имеем манометрическое давление р_ман по оси резервуара А. Поднимаемсядо плоскости уровня 0–0, т.е. вычитаем давление столба воды ρgh, получаем давление р₁, по плоскости уровня 0–0, далее переходим в левое колено U–образного манометра, где р₁ = р₂.

Затем переходим в правое колено манометра, где р₃=р_2; поднимаемся к плоскости 0^'–0^', т.е. вычитаем давление столба ртути ρ_рт gh_рт, получаем давление р₄;переходим по плоскости уровня 0^'–0^' к давлению р₅ = р₄.

В третьих, к полученному давлению р₅ прибавляемдавление столба керосина ρ_кер g(h+h_рт), т.к. опускаемся вниз до оси резервуара В.

Таким образом, получили давление по оси резервуара с керосином, т.е. давление по мановакуумметру.

Представленные рассуждения запишем следующим образом:

р_ман– ρgh – ρ_рт gh_рт +ρ_кер g( h+h_рт)= р_мв.

Подставим численные значения:

р_мв = 0,12·98·10³ – 10³·9,8·0,3 –13,6·10³·9,8·0,2 + 820·9,8·0,5 =

= 9,8·10³ · (1,2–0,3–2,72+0,41) = –1,41·9,8·10³ Па = –13,82 кПа.

Знак «–» свидетельствует о том, что мановакуумметр работает как вакуумметр. Показание вакуумметра р_вак = 13,82 кПа = 0,14 ат (в такой записи индекс «вак» заменяет знак «–»).
Ответ: мановакуумметр работает как вакуумметр и показывает вакуумметрическое давление р_вак=0,14 ат.
Определим зависимость между давлением и напором:

т.к. давление p = ρgh, отсюда напор .

Напор определяется по открытой вертикальной стеклянной трубке малого диаметра, которая называется пьезометром.

Давление,_превышающее_атмосферное,_называется_манометрическим_(избыточным),_которое_измеряется_манометрами_М.'>Давление, превышающее атмосферное, называется манометрическим (избыточным), которое измеряется манометрами М.

Манометрическое давление (р_ман) при решении задач учитывается со знаком «+».

Манометрический напор равен: .

Чтобы представить этот напор нужно вывести пьезометрическую трубку (рис.6, пунктирные линии), отложить вверх h_ман от свободной поверхности жидкости с манометрическим давлением (рис. 6, а), или от места установки манометра М на резервуаре (рис.6,б), или на трубопроводе (рис. 6, в).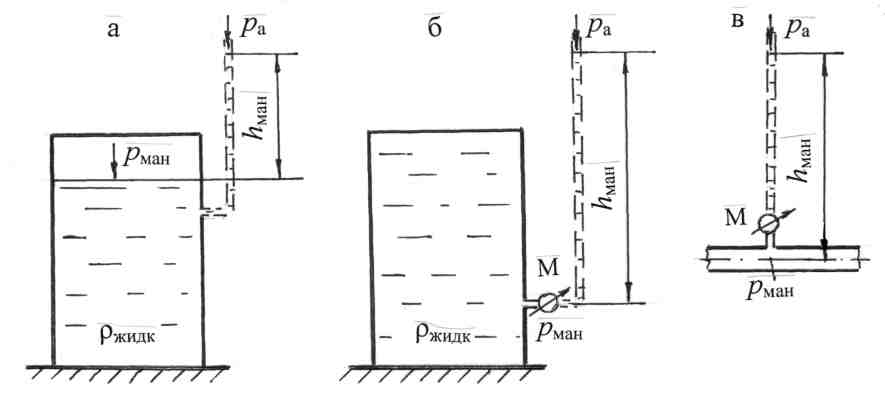


Рис. 6
Давление, недостающее до атмосферного, называется вакууметри-ческим, которое измеряется вакуумметром В. Вакуумметрическое давление при решении задач учитывается со знаком «–».

Вакуумметрический напор равен: .

Чтобы представить этот напор нужно вывести пьезометрическую трубку и отложить вниз h_вак от свободной поверхности с вакууметрическим давлением (рис.7,а) или от уровня установки вакуумметра В (рис.7,б).

Иногда пьезометрическую трубку следует заменить U–образной трубкой (рис. 7,в).

Такой способ перехода от давления к напору (т.е. замена величины давления в жидкости давлением столба жидкости по пьезометру) широко используется при решении задач, как в гидростатике, так и в гидродинамике.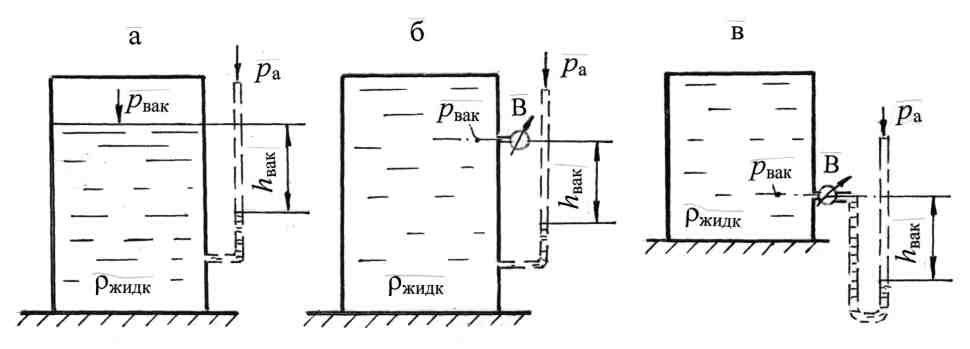


Рис. 7