ПРимеры практических. 1,2 Очники Примеры практ.. "Гидростатическое давление в жидкости"
 Скачать 2.89 Mb. Скачать 2.89 Mb.
|
Примеры решения задач по теме:“Расчёт силы давления жидкости на криволинейные поверхности”Задача 11. Определить величину, угол наклона к горизонту и глубину центра давления для силы давления воды на криволинейную стенку АВ (рис. 15) длиной L = 3,5 м в плоскости, перпендикулярной плоскости чертежа, удерживающую напор Н = 2,1 м. Криволинейная стенка представляет часть цилиндрической поверхности с секторным углом j = 600. Решение. На рис. 15,а показан общий вид криволинейной поверхности, удерживающей напор воды Нс открытой свободной поверхностью. Решение и геометрические построения представлены на рис. 15,б в виде плоского вертикального сечения криволинейной поверхности. Для точности решения чертёж выполнен в масштабе. На примере этой задачи применим методику расчётасилы давления жидкости на криволинейную поверхность; геометрического положения силы, т.е. линии действия силы; глубины погружения центра давления yD (точки приложения силы) и угла наклона α силы давления к горизонту. 1. Выберем два направления – xи y, по которым определим составляющие силы давления Rx и Ry и рассчитаем силу полного давления: а 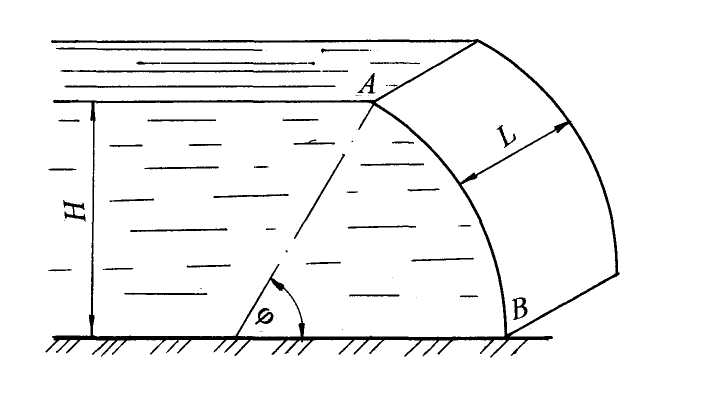 б 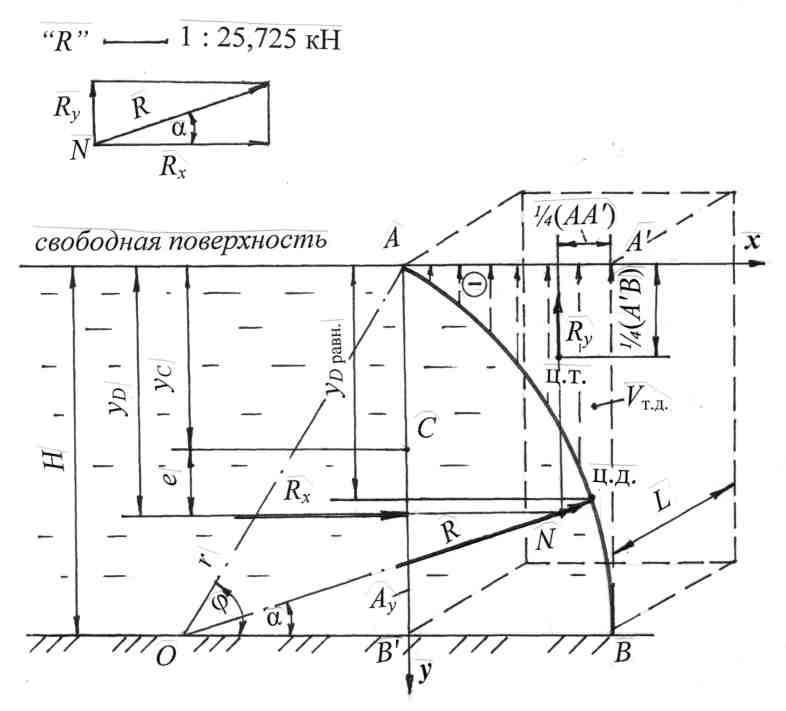 Рис. 15 Для рассматриваемой части цилиндрической поверхности АВ достаточно двух направлений, т.к. поверхность имеет ось симметрии. Ось x, как правило, проводят по свободной поверхности и направляют по линии действия жидкости на криволинейную поверхность. Начало координат примем в т. А, ось x направим вправо. Ось y направим вертикально вниз, т.к. положительное значение координат yC и yD отсчитывается от свободной поверхности по вертикали вниз. 2. Определим горизонтальную составляющую Rx по формуле: Rx = ρgyCAy. Чтобы определить горизонтальную составляющую Rx, спроектируем криволинейную поверхность жидкости на вертикальную плоскость. Получим вертикальную проекцию АВ′ (рис.15,б) в виде прямоугольника высотой Н и шириной (или длиной) L. Найдём силу давления на полученную вертикальную проекцию – это горизонтальная составляющая Rx. Площадь вертикальной проекции равна: Ay = HL. Обозначим на чертеже координату центра тяжести вертикальной проекции – точка С : yC= H/2 = 1,05 м. Рассчитаем горизонтальную составляющую: Определим линию действия горизонтальной составляющей Rx и точку её приложения. Сила Rx действует от жидкости на вертикальную проекцию и приложена в центре давления вертикальной проекции на глубине yD. Глубину погружения центра давления рассчитаем по формуле: где IC– центральный момент инерции вертикальной проекции криволинейной проекции относительно горизонтальной оси, проходящей через центр тяжести С. Момент инерции для прямоугольника: После подстановки данных получим: yD = Эксцентриситет е, т.е. смещение центра давления относительно центра тяжести вертикальной проекции равен: Покажем на рис. 15,б координату (глубину) центра давления yD, эксцентриситет е и положение горизонтальной составляющей Rx. 3. Определим вертикальную составляющую Ry. Вертикальная составляющая силы давления на криволинейную поверхность равна силе тяжести жидкости в объёме тела давления определяется по формуле:Ry = ρgVт.д . Необходимо рассчитать объём тела давления Vт.д. Воспользуемся следующей методикой: чтобы определить объём тела давления и его вид (положительное или отрицательное), из контура криволинейной поверхности проведём вертикальные линии до продолжения свободной поверхности. Заштрихованная часть АА′ВАявляется основанием тела давления. Тело давления представляет криволинейную призму с основанием АА′ВАи высотой, равной длине L криволинейной поверхности. Тело давления построено на несмоченной части криволинейной поверхности, не заполнено водой, поэтому оно считается отрицательным (рис. 15,б). Для отрицательного тела давления основание заштриховано пунктирными линиями со стрелками, направленными вверх. Определим объём тела давления (площади геометрических фигур обозначим буквой S): Vт.д = Sосн. АА′ВА L, где Sосн. АА′ВА – площадь основания тела давления: Sосн. АА′ВА = Sтрап. ОАА′В – Sсект. АОВ; где Sтрап. ОАА′В – площадь трапеции: Sтрап. ОАА′В = Обозначим r = ОА = ОВ– радиус криволинейной поверхности: r = H/sin 60º; r = 2,1/0,866 = 2,42 м, тогда Sтрап. ОАА′В = Sтрап. ОАА′В = 0,75· 2,42· 2,1 = 3,81 м2. Sсект. АОВ – площадь сектора АОВ: Sсект. АОВ = Площадь основания тела давления равна: Sосн. АА′В = 3,81 – 3,06 = 0,75 м2. Рассчитаем объём тела давления и вертикальную составляющую силы давления воды: Vт. д = 0,75 · 3,5 = 2,625 м3; Ry = ρgVт..д; Ry = 103 · 9,8 · 2,625 = 25,725 · 103 Н = 25,725 кН. Покажем на рис. 15,б направление и точку приложения вертикальной составляющей: сила Ry направлена вертикально вверх, т.к. тело давления отрицательное, и она приложена в центре тяжести (ц.т.) тела давления. Центр тяжести основания тела давления (АА′ВА) в вертикальной проекции находится на пересечении линий, проведённых на расстоянии ¼(АА′) и ¼(А′В) (рис. 15,б). 4. Определим величину и положение равнодействующей давления воды R: а) аналитически R = б) геометрическое сложение составляющих сил: Продолжим силы Rx и Ry по линии действия до взаимного пересечения в точке N, через которую пройдёт равнодействующая. Для удобства геометрического сложения сил точку N вынесем за пределы чертежа (рис. 15,б). Из точки N по линии действия отложим горизонтальную составляющую Rx в масштабе и аналогично вертикальную составляющую Ry. Сложение сил проведём по правилу параллелограмма, получим величину силы R в масштабе и её линию действия. Обозначим через α угол наклона равнодействующей к горизонту. Чтобы найти положение центра давленияи координату центра давления для равнодействующей (yDравн), силу R по линии действия параллельно перенесём в точку N на основной чертёж (рис. 15,б) и продолжим её до пересечения с криволинейной поверхностью. Таким образом, точка пересечения силы R с криволинейной поверхностью является центром давления (ц.д.) для равнодействующей. Равнодействующая должна проходить через точку пересечения составляющих (точкаN) и через центр кривизны (точка О), т.е. направлена радиально. Обозначим на рис. 15,б угол α наклона равнодействующей к горизонту. Находим угол α наклона равнодействующейR из параллелограмма сложения составляющих: Рассчитаем координату (глубину) центра давления для равнодействующей: yDравн = Н – rsinα; yDравн = 2,1 – 2,42 · 0,32 = 1,33 м. На рис. 15,б покажем yDравн. Проверим построение в выбранном масштабе. Построение верно. Ответ: равнодействующая давления воды на криволинейную поверхность R = 79,885 кН действует радиально под углом α = 18º47′ к горизонту на глубине yDравн = 1,33 м. Задача 12. Цилиндрический затвор диаметром D = 0,6 м перекрывает прямоугольное отверстие в вертикальной стенке, удерживающей напор воды (рис. 16). Высота отверстия равна диаметру затвора, длина отверстия L = 2,0 м. Уровень воды над верхней кромкой затвора h = 0,2 м. Затвор может поворачиваться относительно горизонтальной оси и, перемещаясь горизонтально, открывать отверстие. Определить величину и угол наклона к горизонту силы давления воды на цилиндрический затвор. Решение. На рис. 16,а показан общий вид затвора. Решение представим для вертикального сечения затвора, при этом длина затвора L перпендикулярна плоскости чертежа (рис. 1.27,б). Для наглядности и лучшего понимания чертёж выполнен в удобном для построения масштабе. В соответствии с теоретическими положениями раздела 1.3.1 применим методику расчёта силы давления жидкости на криволинейные поверхности. .1. Выбираем два направления xиy, по которым определим составляющие силы давления жидкости. Сила полного давления R равна: Для данной цилиндрической поверхности достаточно двух направлений, т.к. цилиндр имеет ось симметрии. Ось x направляем по свободной поверхности вправо по направлению действия жидкости. Ось y направляем вертикально вниз, т.к. положительное значение координат (глубин) отсчитывается от свободной поверхности вниз (рис. 16,б). 2. Определяем горизонтальную составляющую Rx по формуле: Rx = ρgyCAy . Криволинейную поверхность АВспроектируем в жидкости на вертикальную плоскость. Получим вертикальную проекцию Рассчитаем силу давления воды на эту вертикальную проекцию – это горизонтальная составляющая Площадь вертикальной проекции равна: Ay = DL. Координата, или глубина погружения центра тяжести точки С этой проекции: yC = h + D/2 = 0,5 м. Покажем на чертеже yC . Рассчитаем горизонтальную составляющую: Rx = ρg (h + D/2)DL; Rx= 103·9,8·0,5·0,6·2,0 = 5,88·103 Н = 5,88 кН. Определяем глубину погружения центра давления yD для горизонтальной составляющей, т.е. глубину точки приложения силы Rx по формуле: где IC - центральныймомент инерции относительно горизонтальной оси, проходящей через центр тяжести С вертикальной проекции криволинейной поверхности. Момент инерции для прямоугольника: После подстановки данных получим: Покажем на чертеже yD, эксцентриситет еи положение силы Rx. Горизонтальную составляющую Rx можно определить также графо-аналитическим методом, согласно формуле: Rx = Sэп L. Определим давление воды в точках Построим эпюру гидростатического давления. Эпюра представляет собой призму с основанием в виде трапеции и высотой L. Площадь трапеции обозначим через S. Тогда: Получили формулу, соответствующую формуле (1.23). Находим графически положение центра давления. Глубина погружения центра давления совпадает с положением центра тяжести эпюры в виде трапеции (рис. 16, в). Находим координату центра тяжести эпюры: 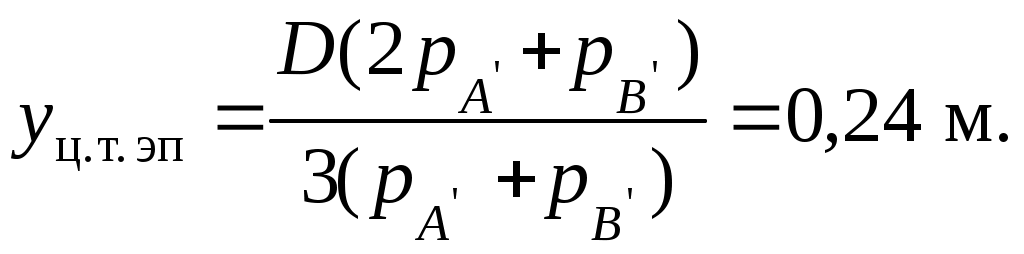 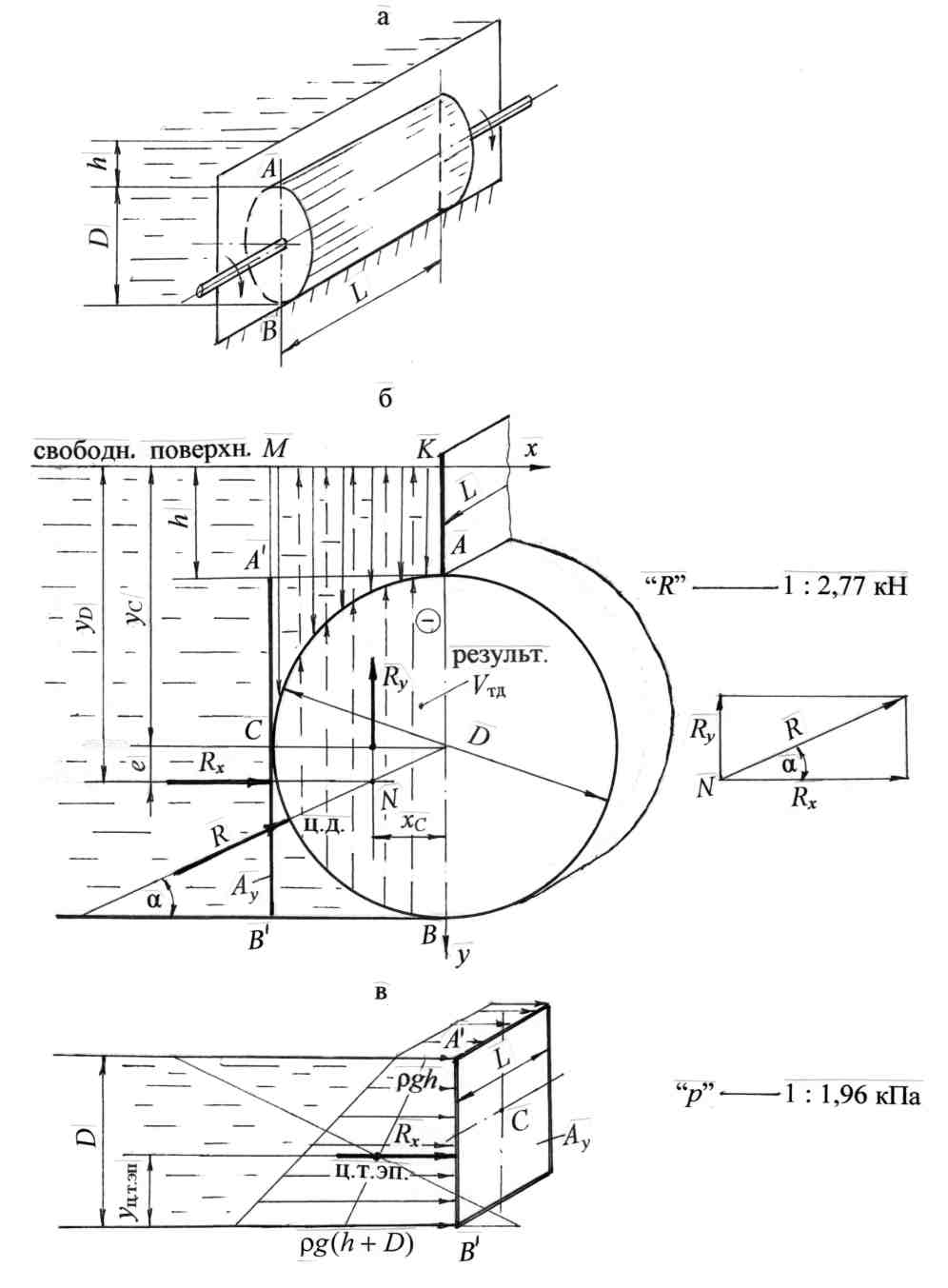 Рис. 16 Центр тяжести трапеции можно определить геометрическим построением. На рис. 16,в покажем yц.т.эп, получим yD = h+D – yц. т. эп = 0,56 м. Расчёты горизонтальной составляющей Rx и глубины погружения центра давления yD аналитическим и графоаналитическим методами совпали. 3. Определяем вертикальную составляющую Ry силы давления воды на цилиндрическую поверхность по формуле: Ry = ρgVт. д. Криволинейная поверхность имеет две части – АС иСВ. Строим тело давления для части АС. Из контура криволинейной части АС проводим вертикальные линии до свободной поверхности жидкости, получим реальное (положительное) тело давления в виде криволинейной призмы с основанием АКМСА, построенное на смоченной поверхности АСи заполненное водой. Стрелки в эпюре тела давления направляем вниз. Для части криволинейной поверхности СВ снова проводим вертикальные линии до свободной поверхности, получим отрицательное тело давления в виде криволинейной призмы с основанием ВСМКВ, т.к. оно построено на несмоченной поверхности и не заполнено жидкостью. Стрелки в эпюре тела давления покажем пунктиром и направим вверх. Анализ построения двух тел давления показывает, что в объёме АКМСА два тела давления взаимно уничтожаются (сокращаются, компенсируются). Результирующее тело давления отрицательное в виде полуцилиндра объёмом равным: Вертикальная составляющая Ry равна: Показываем линию действия и точку приложения Ry. Вертикальная составляющая сила приложена в центре тяжести тела давления и направлена вверх. Центр тяжести полуцилиндра находится на расстоянии от оси цилиндра: xC = 4r/3π = 0,13 м. Показываем на чертеже расстояние xC - центр тяжести полуцилиндра и направление силы Ry (рис. 16,б). 4. Определяем величину равнодействующей силы давления воды на цилиндрический затвор: Чтобы найти линию действия, направление и точку приложения равнодействующейсилыR, по линии действия продолжим силы Rx и Ry до взаимного пересечения, получим точку N. Геометрическое сложение сил проведём вне чертежа. Вынесем точку N и покажем сложение сил в масштабе. Параллельно по линии действия силу R перенесём в точку N на основном чертеже и продолжим её до пересечения с криволинейной поверхностью. Равнодействующая сила Rдолжна пройти через точку пересечения составляющих и центр криволинейной поверхности. Точка пересечения равнодействующей силы с цилиндрической поверх-ностью является центром давления. Угол α наклона равнодействующей силы R найдём через tg α : |
