ПРимеры практических. 1,2 Очники Примеры практ.. "Гидростатическое давление в жидкости"

• Название: "Гидростатическое давление в жидкости"
• Анкор: ПРимеры практических
• Дата: 07.05.2022
• Размер: 2.89 Mb.
• Имя файла: 1,2 Очники Примеры практ..doc
• Тип: Задача; #516168
• страница: 2 из 8

Примеры решения задач по теме:

“Расчёт силы давления жидкости на плоские поверхности”

Задача 6
Прямоугольная крышка АВ (рис. 8), расположенная под углом

α = 60⁰ к горизонту, перекрывает патрубок закрытого резервуара с водой. Высота патрубка h = 600 мм, ширина b = 400 мм.

Крышка может поворачиваться вокруг цилиндрического шарнира А. Высота уровня воды над шарниром а = 200 мм.

Давление на поверхности воды соответствует показанию U–образного ртутного манометра h_рт = 80 мм.

Определить силу натяжения троса Т для удержания крышки АВ в закрытом положении. Угол натяжения троса β = 45⁰. Принять плотность воды ρ = 10³ кг/м³.

Решение.

Чтобы рассчитать силу натяжения троса Т для удержания крышки АВ в закрытом положении, нужно определить силу от внешнего давления R₀и силу давления воды R_ж.

Рассмотрим аналитический способ расчёта силы давления и глубины погружения центра давления.

Методика расчёта силы давления:

– рассчитывается сила давления жидкости и сила от внешнего давления, при этом на чертеже обозначаются центральные оси плоской стенки и глубина погружения центра тяжести стенки от свободной поверхности h_С;

– определяются точки приложения сил, на чертеже обозначается точка приложения силы давления жидкости, т. е. центр давления, и глубина погружения центра давления h_D;

– показывается линия действия и направление сил.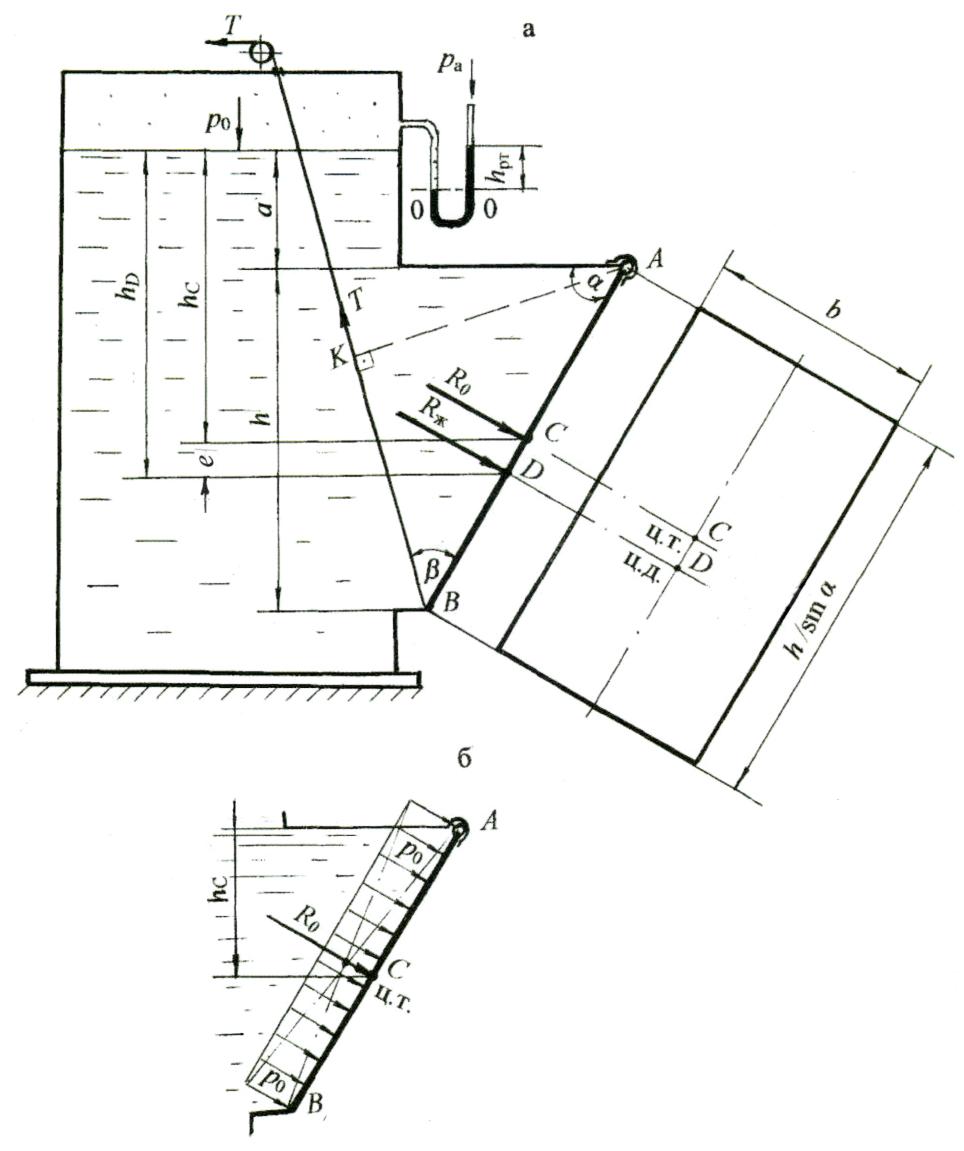

Рис. 8

Известно, что сила давления жидкости всегда направлена по внутренней нормали к поверхности.

1. Определим силу от внешнего давления R₀.

Значение давления р₀ по показанию U–образного манометра получим из условия равновесия жидкости относительно плоскости уровня 0–0.

Давление р₀ является избыточным:

р₀ = ρ_ртgh_рт;р₀= 13,6×10³×9,8×0,08 = 10,66×10³ Па = 10,7 кПа.

Значение р₀ можно получить другим способом, а именно перевести показание манометра 80 мм рт. ст. в Па:

p₀ = 80×133,3 = 10,66×10³ Па = 10,7 кПа.

Сила от внешнего давления равна:

R₀ = p₀ A,

где А – площадь крышки, м².

Для наглядности крышку совместим с плоскостью чертежа, тогда ширина крышки равна b, а высота равна:

h/sin α = h/sin60⁰ = 0,693 м.

Площадь крышки равна: А = bh/sin 60⁰.

Сила от внешнего давления

R₀= 10,7×0,4×0,693 =2,97 кН.

Покажем линию действия и точку приложения силы R₀.

Эпюра давления р₀ представляет равномерно распределённую прямоугольную нагрузку, равнодействующая от такой нагрузки R₀ проходитчерез центр тяжести эпюры и приложена в центре тяжести стенки на глубине h_С (рис. 8,б).

Сила R₀ направлена по нормали от жидкости на стенку, как сила внешнего, избыточного давления.

2. Определим силу давления жидкости R_ж по формуле:

R_ж = ρgh_CA,

где h_C=(a + h/2) = 0,5 м; глубину погружения центра тяжести стенки в жидкость (h_C ) отсчитываем от свободной поверхности (рис. 8, а).

Подставим значения:

R_ж=ρg(a + h/2) hb/sin α ;

R_ж = 10³ × 9,8 × 0,5 × 0,693 × 0,4 = 1,36 × 10³ H = 1,36 кН.
Чтобы показать геометрическое положение силы давления жидкости R_ж, рассчитаем глубину погружения центра давления h_D, т.е. точки приложения силы R_ж по формуле:



где – центральный момент инерции прямоугольной крышки относительно горизонтальной оси, проходящей через центр тяжести крышки С определяется по формуле:



Подставив все параметры, и сделав сокращения, получим глубину погружения центра давления h_D:

h_D= h_C + h²/12h_C = 0,5 + 0,06 = 0,56 м.

Эксцентриситет равен е = h²/12h_C ,

т.е. понижение центра давления относительно центра тяжести равно:

е = 0,06 м = 60 мм.

Покажем на чертеже (рис. 1.10,а) величины h_D и е.

Сила давления жидкости R_ж приложена в центре давления (точка D) на глубине h_D, действуетпо нормали из жидкости на крышку.

3. Рассчитаем силу натяжения троса Т.

Составим уравнение равновесия механики – сумма моментов сил относительно шарнира А равна нулю: ΣM_A = 0.

От каждой силы R₀,R_жи Т берётся момент относительно точки А:

R₀× AC + R_ж× AD – T × AK = 0;



После преобразований получим: Т = 3,25 кН.
Ответ: для удержания крышки АВ в закрытом положении необходима сила натяжения троса Т 3,25 кН.
Рассмотрим другой вариант в условии задачи 6, когда показание

U–образного манометра будет представлено так, что уровень ртути в левом колене манометра будет выше, чем в правом на величину h_рт (рис. 9).

Из условия равенства давления относительно плоскости уровня 0–0 (рис. 9) запишем:

р_0абс + ρ_ртgh_рт = р_а или р_а – р_0абс = ρ_ртgh_рт;

р_а – р_0абс = р_вак, значит, р_вак = ρ_ртgh_рт .
На поверхности воды действует вакуумметрическое давление.

Это значит, что сила от внешнего вакуумметрического давления будет приложена в центре тяжести стенки, но направлена по нормали внутрь жидкости (рис. 10).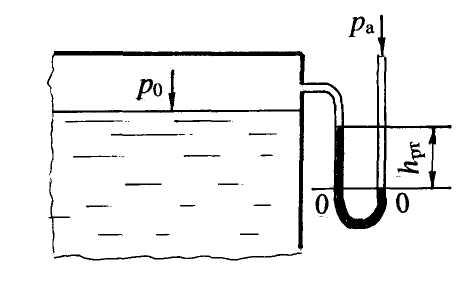




Рис. 9
В уравнении моментов сил относительно точки А момент от силы R₀ нужно учитывать со знаком минус, как и момент от силы Т:

R_ж× AD – R₀× АC – T ×AK = 0.

Возможно, получится такой случай, когда не потребуется трос, а момент от силы давления жидкости будет равен или меньше момента от внешней вакуумметрической силы.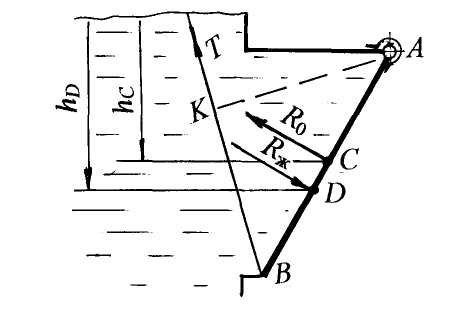



Рис. 10


Под действием вакуумметрического давления на поверхности воды крышка будет в закрытом положении, в этом случае

R_ж×AD = R₀×AC.

Из предыдущего расчёта имеем:

R_ж = 1,36 кН.

Можно рассчитать предельный вакуум для удержания крышки в закрытом положении.

Из приведённого равенства следует:

R₀ = 1,632 кН.

Зная, что R₀ = p_вак А, определим р_вак:

p_вак = R₀/A; A = bh/sin60° = 0,2772 м²; тогда р_вак = 5,89 кПа.

Рассчитаем высоту столба ртути h_рт вманометре при котором крышка будет в закрытом положении под действием вакуума на поверхности воды (рис. 10): р_вак = r_рт gh_рт, отсюда h_рт = 0,044 м = 44 мм.


Задача 7.
В торцевой стенке цистерны, заполненной бензином, предусмотрена плоская круглая крышка диаметром d= 1,6 м, укреплённая при помощи болтов (рис. 11). На поверхности бензина действует вакуумметрическое давление р_вак = 0,2 ат. Принять плотность бензина r_бенз =720 кг/м³

Определить силу давления бензина на крышку и точку приложения силы, если высота уровня бензина над нижней кромкой крышки H = 2,0 м.

Для определения равнодействующей силы давления воспользуемся аналитическим методом.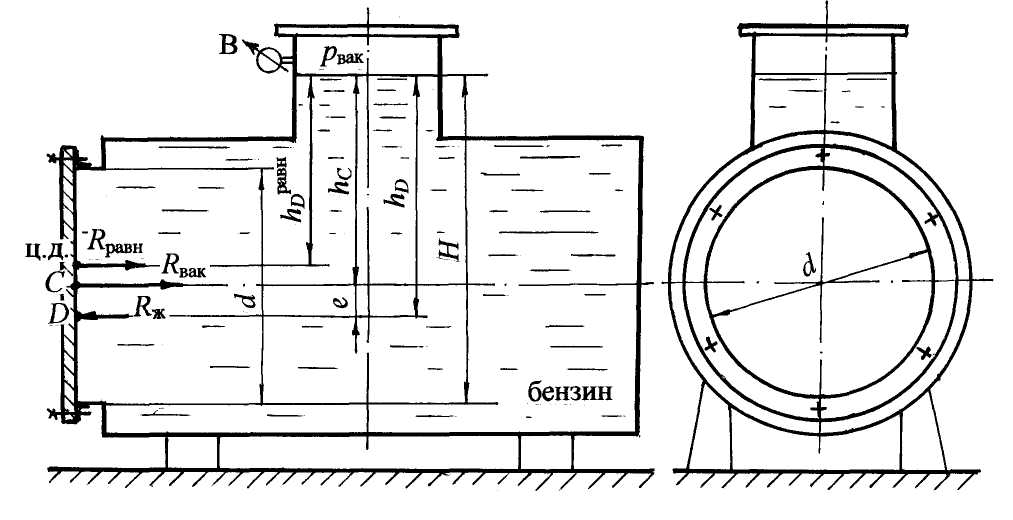


Рис. 11

Решение.
Равнодействующая сила, т.е. сила полного давления равна:

R_равн = р₀ А + rgh_C А или

1. Определим силу от внешнего, вакуумметрического давления:

R₀ = R_вак = р_вак А,

где А – площадь крышки; А = pd²/4 = 3,14×1,6²/4 = 2,0 м².

R_вак = 0,2×98×10³×2,0 = 39,4×10³ Н = 39,4 кН.

Покажем линию действия R_вак. Эта сила приложена в центре тяжести крышки (т. С) и направлена по нормали внутрь жидкости, как сила вакуумметрического давления (сила со знаком минус).

2. Рассчитаем силу давления бензинаR_ж на круглую крышку по формуле: R_ж = r_бенз gh_CA,

где h_С– глубина погружения центра тяжести крышки в жидкость, отсчитанная от свободной поверхности.

Определяем h_C по чертежу (рис. 11):

h_C= H – d/2 = 1,2 м; R_ж = 720·9,8·1,2·2,0 = 16,9·10³ Н = 16,9 кН.

Покажем линию действия силы давления бензина R_ж и точку приложения силы.

Сила давления жидкости R_ж приложена в центре давления на глубине h_Dи направлена по нормали из жидкости.

Глубина погружения центра давления равна:



где α = 90˚; sin α = 1,0 для вертикальной крышки;

I_C– центральный момент инерции круглой крышки относительно горизонтальной оси, проходящей через центр тяжести крышки С



После подстановки данных в выражение h_D получим:

h_D = 1,2 + 0,13 = 1,33 м.

Эксцентриситет е = 0,13 м. Покажем на чертеже величины h_D, e и R_ж.

3. Определим величину и положение равнодействующей силы R_равн (или силы полного давления) путём векторного сложения сил R_вак и R_ж:



R_равн = R_вак – R_ж = 22,5 кН.
Положение равнодействующей силы можно определить, пользуясь теоремой Вариньона: момент равнодействующей силы равен сумме составляющих моментов сил.

Составим сумму моментов сил относительно оси, проходящей по свободной поверхности бензина.

Введём обозначение: пусть – глубина погружения центра давления для равнодействующей силы, тогда

M_{R равн} = M_{R вак} + М_Rж ,

R_равн h_D^равн = R_вакh_C – R_жh_D,

отсюда h_D^равн = (R_вакh_C – R_жh_D)/R_равн .

После подстановки численных значений получим h_D^равн = 1,1 м.
Покажем на чертеже глубину погружения h_D^равн, центр давления для равнодействующей силы и линию действия равнодействующей R_равн по нормали внутрь жидкости.
Ответ: R_равн= 22,5 кН; h_D^равн = 1,1 м.

Задача 8.
Квадратный затвор АВ (рис. 12) со стороной а=1,2м, перекрывающий выход воды из зумпфа, укреплён шарнирно и может поворачиваться относительно оси, проходящей через центр затвора.

Определить силу F, которую нужно приложить на расстоянии 0,1а от нижнего края затвора, чтобы удерживать затвор в закрытом положении при глубине воды перед затвором h = 1,5 м.

Решение.
Слева от затвора имеем открытую свободную поверхность с атмосферным давлением, справа – щит, который также находится под действием атмосферного давления, поэтому при определении силы давления будем учитывать только силу давления жидкости (силу от атмосферного давления в таком случае не учитывают).

Решение задачи проводим аналитическим и графоаналитическим методами.

1. 
   Аналитический метод расчёта:
   

а) Рассчитаем силу давления воды по формуле:

R_ж = ρgh_C A,

где А – площадь затвора: A = a² = 1,44 м²;

h_C – глубина погружения центра тяжести затвора:

h_C= h – a/2 = 0,9 м;

покажем h_C на чертеже.

R_ж = 10³·9,8·0,9·1,44 = 12,7·10³ Н = 12,7 кН;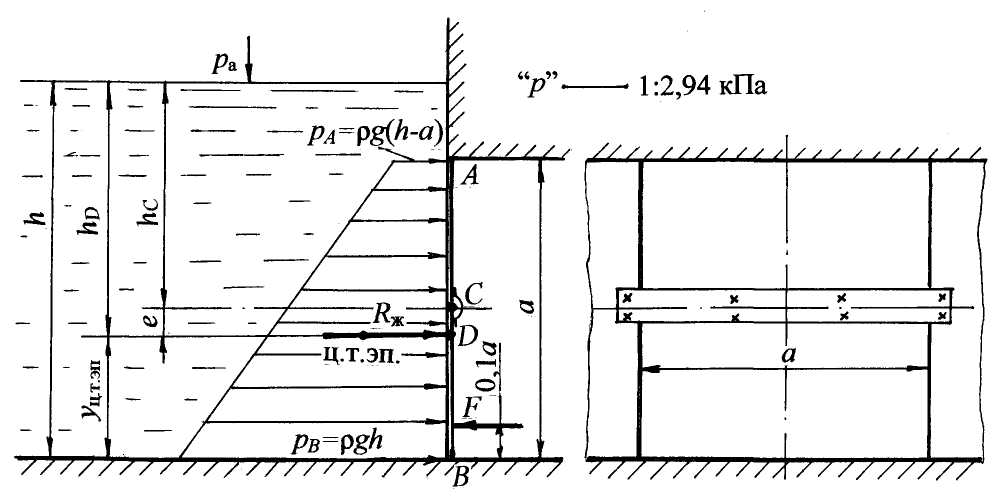



Рис. 12
б) Определим глубину погружения центра давленияh_D, т.е. точку приложения силы давления R_ж по формуле (1.11):



где α = 90˚; sin α = 1,0; I_C– центральный момент инерции относительно горизонтальной оси, проходящей через центр тяжести С ;

для квадратного затвора: I_C= a⁴/12 .

После подстановки всех значений в выражение h_D и соответствующих сокращений получим: ; h_D = 0,9 + 0,13 = 1,03 м.

Эксцентриситет е =0,13 м.

Покажем на чертеже величины h_D, e, силу R_ж , приложенную в центре давления (т. D).

в) Определим силу Fдля удержания затвора в закрытом положении, т.е. в состоянии равновесия, составив уравнение равновесия механики, т.е. cумма моментов сил относительно шарнира С равна нулю:

ΣМ_С = 0; R_ж е – F·0,4а = 0, отсюда F= 3,44 кН.

2. 
   Графоаналитический метод расчётасилы давления воды R_ж и глубины погружения центра давления h_D.
   

а) Определим давление воды в точках Аи В:
р_А = ρg(h–a); р_А = 10³·9,8·0,3 = 2,94·10³ Па = 2,94 кПа;

р_В = ρgh; р_В = 10³·9,8·1,5 = 14,7 кПа.
б) Строим эпюру гидростатического давления воды.

Для построения эпюры по нормали к стенке откладываем в масштабе величину давления р_Аи р_В; соединяем полученные значения наклонной прямой, т.к. закон изменения давления по глубине линейный и заштриховываем полученную площадь горизонтальными штриховыми линиями; стрелками обозначим направление действия давления.

Получим эпюру давления воды в виде трапеции в вертикальной плоскости, в объёмном представлении эпюра является трапециевидной призмой.

в) Рассчитаем силу давления воды R_ж .
Сила давления равна объёму трапециевидной призмы и проходит через центр тяжести этой призмы, согласно формуле:

R_ж = S_эп а;



После подстановки данных получим: S_эп = 10,6 кПа·м; R_ж = 12,7 кН.

г) Определим положение центра давления.

В соответствии с графоаналитическим методом, сила давления жидкости проходит через центр тяжести эпюры гидростатического давления.

Положение центра тяжести эпюры в виде трапеции определяется по формуле: .

В соответствии с рисунком, глубина погружения центра давления h_D

равна: h_D = h –y_ц.т.эп = 1,5 – 0,47 = 1,03 м.
Таким образом, аналитический и графоаналитический методы расчёта силы давления R_ж и глубины погружения центра давления h_D дают одинаковые значения.
Ответ: сила F 3,44 кН.
Задача 9.
Определить равнодействующую давления воды и положение центра давления на грани плотины АВС(рис. 13), удерживающей следующие напоры: Н₁ = 3,0 м; Н₂ = 2,0 м.

Угол наклона к горизонту наклонной грани плотины α = 60˚.

Длина плотины в плоскости, перпендикулярной плоскости чертежа,

l = 10 м. Решение выполнить графоаналитическим методом.
Решение.
Графоаналитический метод решения предусматривает выполнение чертежа в масштабе. Представим в выбранном масштабе сечение плотины и действующие напоры.

Равнодействующая давления воды на грани плотины определится путём векторного сложения сил, действующих на наклонную R_АВ и вертикальную R_ВС грани плотины:



Расчёт силы давления на плоские поверхности проводим графоаналитическим методом по следующей методике.

1. Определяем давление воды в точках плотины А, В, С:

р_А = 0; р_В = ρgH₁; р_С =ρg (H₁ + H₂);

р_В = 10³·9,8·3,0 = 29,4·10³ Па = 29,4 кПа;

р_С= 10³·9,8·5,0 = 49,0·10³ Па = 49,0 кПа.

2. Строим эпюры гидростатического давления воды.

Известно, что давление действует нормально к плоской поверхности (рис. 13).

В выбранном масштабе откладываем величину давления в точках А, В, С. Эпюра давления на наклонную грань плотины представляет треугольную нагрузку.

Основание треугольника соответствует величине давления:

р_В = ρgH₁,

т.е. давлению в точке В, отложенному по нормали к наклонной грани.

При построении эпюры давления на вертикальную грань давление в точке В откладываем также по нормали к вертикальной грани плотины.

В точке Соткладываем давление по нормали к вертикальной грани плотины: р_С = ρg (H₁ + H₂).

Для вертикальной грани эпюра давления представляет нагрузку в виде трапеции (рис. 13).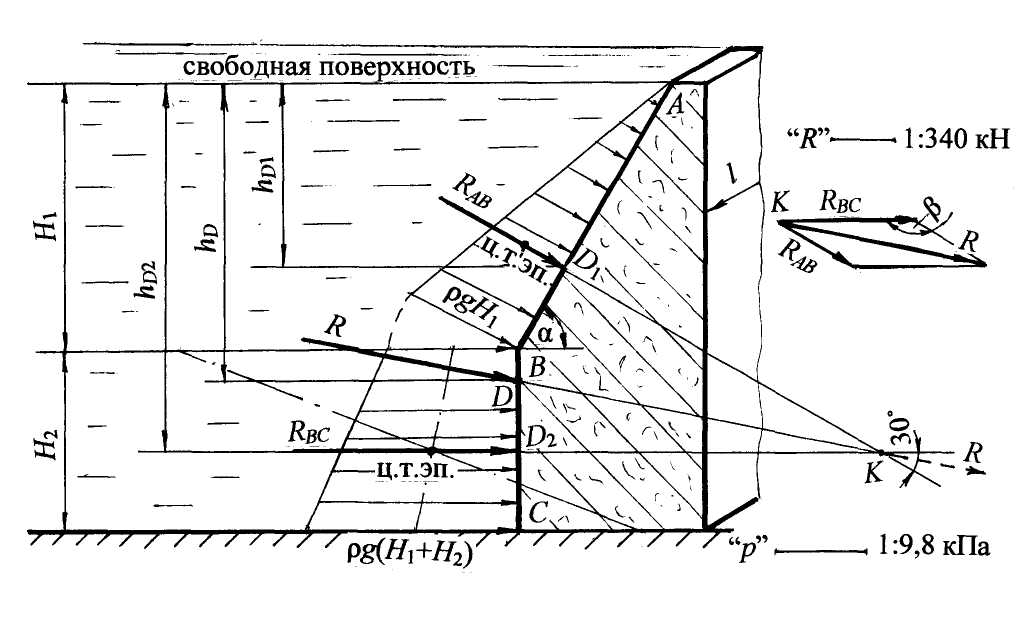

Рис. 13

1. 
   Рассчитаем силы давления воды на грани плотины согласно формуле (1.16):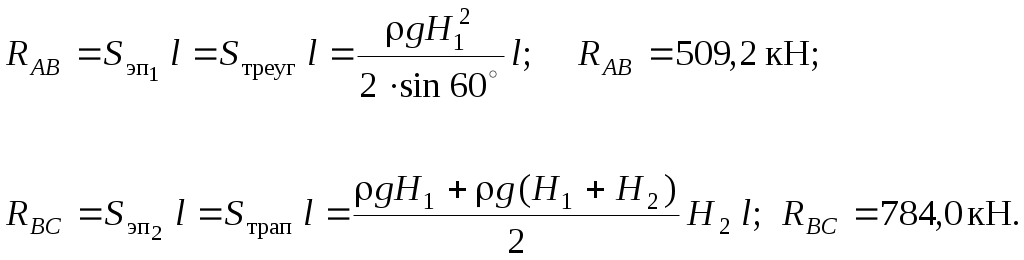
   

3. 
   Показываем линию действия сил R_AB и R_BC .
   

Сила давления жидкости проходит через центр тяжести эпюры гидростатического давления.

Центр тяжести эпюры в виде треугольной нагрузки расположен на расстоянии 2/3 высоты треугольника, т.е.

2/3AB= 2/3·(H₁ /sin 60˚).

Находим в масштабе центр тяжести треугольника и показываем линию действия силы R_AB.

Эта сила проходитчерез центр тяжести треугольника и приложена нормально к наклонной грани плотины в центре давления (точка D₁). Показываем на чертеже глубину погружения центра давления:

h_D1 = 2/3 Н₁= 2,0 м.

Для определения положения центра тяжести эпюры в виде трапеции можно воспользоваться табл. 3 (приложение).

Поскольку метод решения задачи графоаналитический, рассмотрим геометрический способ определения центра тяжести трапеции (рис. 13) построение показано тонкими штрихпунктирными линиями):

а) к меньшему основанию трапеции на его продолжении в любую сторону прибавляем большее основание трапеции;

б) к большему основанию трапеции в противоположную сторону прибавляем меньшее основание;

в) соединяем полученные две точки прямой линией;

г) через середины оснований трапеции проводим вторую линию;

д) точка пересечения двух линий построения является центром тяжести эпюры давления в виде трапеции.

Показываем центр тяжести трапеции и через эту точку проводим силу R_BCпо нормали к вертикальной грани. Учитывая масштаб действующих напоров, находим величину h_D2 = 4,1 м.

5. Определяем величину и линию действия равнодействующей силыR путём векторного сложения силR_ABиR_BC.

Продлим линии действия силы до взаимного пересечения в точке К.

По линии действия откладываем величины сил в удобном принятом масштабе и складываем их по «правилу треугольника» или по «правилу параллелограмма».

Может быть вариант, когда точка пересечения составляющих сил расположена так, что её следует вынести за пределы чертежа, как представлено в данном решении, и далее произвести сложение векторов сил. Затем по линии действия равнодействующую R параллельно перенести в точку пересечения составляющих и определить точку пересечения равнодействующей с плоской поверхностью.

В данной задаче (рис. 13) силу R, найденную путём векторного сложения, переносим параллельно в точку пересечения составляющих К, силу R продолжаем по линии ее действия до пересечения с гранью плотины в точке D.

Точка D является центром давления для равнодействующей R.Глубину погружения центра давления h_D следует определить по масштабу. Величину равнодействующей силы определим по принятому масштабу при сложении сил.

По масштабу глубина погружения центра давления h_D = 3,5 м.

Проверим значение силы Rаналитическим расчётом, пользуясь теоремой косинусов.

Угол между силами R_AB и R_BC при их сложении по «правилу треугольника» равен β = 150˚ (рис. 1.15).

Определим равнодействующую давления воды:

;

cos 150˚= – cos 30˚= – 0,866;



Проверив значение силы Rпо масштабу, получим c допустимой точностью такое же значение.

Ответ: Сила давления воды на напорную грань плотины R=1251,2 кН. Глубина погружения центра давления h_D= 3,5 м.
Задача 10.

Определить величину, направление и точку приложения силы давления воды на наклонную стенку АВ(рис. 14), удерживающую напоры: слева напор Н = 4,5 м, справа напор h =1,5 м. Длина стенки в плоскости, перпендикулярной плоскости чертежа,l= 5,0 м. Угол наклона стенки к горизонту α = 45˚. Применить графоаналитический метод решения.

Решение.

Методика расчёта силы давления на плоские прямоугольные поверхности графоаналитическим методом рассмотрена в задаче 9. Решение данной задачи будет представлено более кратко.

Равнодействующую давления воды определим путём построения результирующей эпюры гидростатического давления.

1. Определяем давление воды в характерных точках:

слева р_А = 0; р_В^сл = ρgН= 10³·9,8·4,5 = 44,1·10³ Па = 44,1 кПа;

справа р_N = 0; р_В^спр = ρgh =10³·9,8·1,5 = 14,7 ·10³ Па =14,7 кПа.

2. Строим эпюры давления воды слева и справа.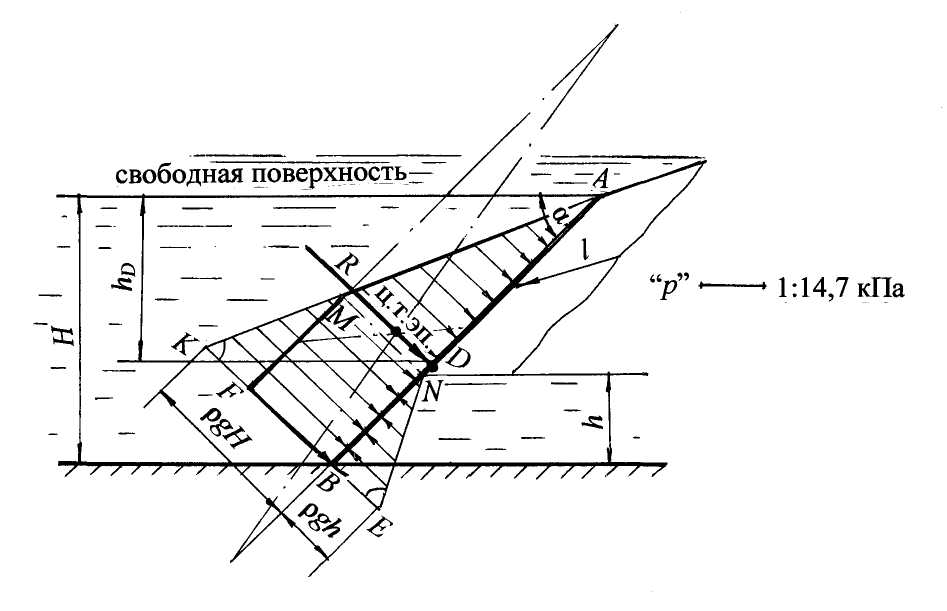



Рис. 14
Слева эпюра давления представляет нагрузку в виде прямоугольного треугольника АВК с основанием равным:

КВ = р_В^сл = ρgH.

Это давление откладываем в масштабе по нормали к стенке АВ; стрелками показываем направление давления из жидкости на стенку.

Справа эпюра давления также представляет нагрузку в виде прямоугольного треугольника NВE с основанием равным:
ВЕ = р_В^спр = = ρgh.
Давление справа является противодавлением, поэтому направление давления соответственно показано стрелками навстречу давлению слева, по аналогии из жидкости на плоскость.

Углы наклона эпюр одинаковые, т.к. слева и справа находятся жидкости одинаковой плотности, т.е. вода.

Из построенных эпюр следует, что из эпюры давления слева (из треугольника АВК) можно вычесть эпюру давления справа (треугольник NВE). Результирующая эпюра давления представляет трапецию FMAВ (рис. 14).

3. Рассчитываем равнодействующую давления воды по формуле:

.

При построения эпюр имеем:

AB = H/sin α = H/sin 45˚ = 6,36 м;

FM = NB = h/sin α = h/sin 45˚ = 2,15 м;

FB = p_В^сл – р_В^спр = ρg (H–h) = 29,4 кПа.

.

4. Показываем линию действия равнодействующей R.

Сила проходит через центр тяжести эпюры в виде трапеции.

В задаче рассмотрено геометрическое определение центра тяжести трапеции.

Путём геометрических построений покажем центр тяжести трапеции и через него проведём равнодействующую R по нормали к стенке АВ.

Точка пересечения линии действия равнодействующей с плоской стенкой является центром давления т. D.

Глубину погружения центра давления h_D = 2,87 м можно определить: либо по масштабу; либо вычислитьпо формуле; либо через координаты центров тяжести сложной фигуры, состоящей из прямоугольника и треугольника.

В данном учебном пособии такой метод будет представлен при определении силы давления на криволинейные поверхности.
Ответ: равнодействующая давления воды R = 625,5 кН, глубина погружения центра давления h_D = 2,87 м.

При расчёте силы давления жидкости на плоские, а в дальнейшем и на криволинейные поверхности, могут быть случаи, когда резервуар закрыт и находится под напором; кроме того, отсутствует свободная поверхность жидкости, но известно показание прибора для измерения давления на определённом уровне.

Такими приборами могут быть пьезометр, манометр механический или жидкостный, вакуумметр, мановакуумметр.

В этом случае рациональным считается метод расчёта силы давления и её положения, при котором производится перевод давления из ат, бар, мм рт. ст. и т. п. в давление столба жидкости по пьезометру.

Пьезометр – это открытая стеклянная трубка, в которой по уровню жидкости можно определить положение условнойсвободной поверхности, от которой отсчитываются глубина погружения центра тяжести плоской поверхности и центра давления для силы давления жидкости.

Пример такого расчёта силы давления жидкости представлен в задаче 11.