ПРимеры практических. 1,2 Очники Примеры практ.. "Гидростатическое давление в жидкости"

• Название: "Гидростатическое давление в жидкости"
• Анкор: ПРимеры практических
• Дата: 07.05.2022
• Размер: 2.89 Mb.
• Имя файла: 1,2 Очники Примеры практ..doc
• Тип: Задача; #516168
• страница: 5 из 8

Ответ: сила давления воды на цилиндрическую поверхность R = 60,5 кН радиально направлена под углом α = 39˚, приложена на глубине


Рассмотрим случай определения силы давления жидкости на криволинейную поверхность в виде полусферы на примере решения задачи 15.
Задача 15.
Определить силу давления нефти на цилиндрическую поверхность АВ (рис. 19), а также угол наклона силы к горизонту, если слева уровень нефти H₁ = D =1,2 м, справа – H₂ = D/2 = 0,6 м.

Длина цилиндрической поверхности в плоскости, перпендикулярной плоскости чертежа, L=4,0 м. Принять плотность нефти ρ_нефт = 900 кг/м³.
Решение.
На рис. 19,а представлен общий вид цилиндрической поверхности длиной L, воспринимающей давление нефти с двух сторон.

В случае действия жидкости с двух сторон целесообразно определить составляющую R_x как геометрическую сумму горизонтальных сил слева и справа , и вертикальную составляющую R_y через объём результирующего тела давления, затем геометрически сложить R_xи R_y и получить результирующую силу давления Rи её положение.

Рассчитать силу давления жидкости на криволинейную поверхность сначала слева, затем справа, геометрически сложить эти составляющие для определения равнодействующей силы и её положения более трудоёмко, как аналитически, так и геометрически.
Применим методику расчёта силы давления на криволинейную поверхность, используя более рациональный способ решения.
1. Покажем два направления x и y(рис. 19,б), по которым определим составляющие силы давления с последующим их геометрическим сложением:

2. Определим величину и положение горизонтальной составляющей R_x. Расчёт проведём графоаналитическим методом:

Определим силу давления нефти слева .

Криволинейную поверхность АВ спроектируем на вертикальную плоскость в жидкости; получим вертикальную проекцию в виде прямоугольника высотой H₁ и длиной (шириной) L (рис. 19,б).
Давление нефти в точках и равно:

р_А′ = 0; р_В′ = ρ_нефт gН₁;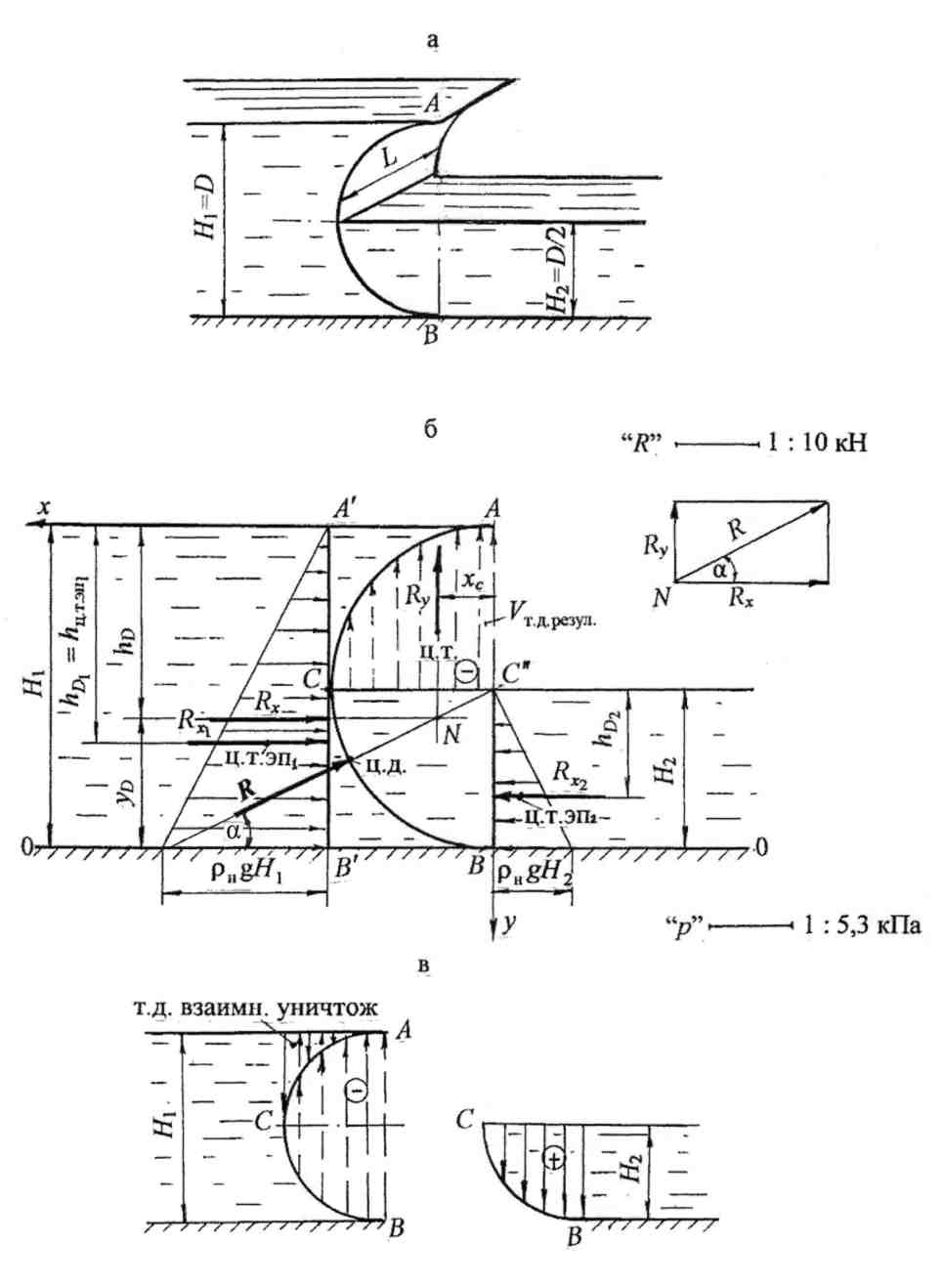

.



Рис. 19.

Строим эпюру давления слева. Откладываем по нормали к вертикальной проекции величину давления в характерных точках в масштабе и соединяем полученные точки наклонной прямой.

Эпюра давления представляет треугольную призму с основанием в виде треугольника и высотой, равной L. Заштриховываем эпюру, стрелками показываем направление давления нефти слева направо (рис. 19,б)

Силу рассчитаем по формуле (1.16):

Покажем линию действия силы . Сила проходит через центр тяжести эпюры, т.е. через центр тяжести треугольника.

Глубина погружения центра давления для силы :



На чертеже (рис. 19,б) покажем глубину и линию действия силы .

Сила направлена по нормали к вертикальной проекции слева направо (из жидкости на вертикальную проекцию).

Определим силу давления нефти справа

Криволинейную поверхность СВ проектируем на вертикальную плоскость жидкости, получим вертикальную проекцию в виде прямоугольника высотой H₂ и длиной L.

Рассчитаем силу Давление в характерных точках:


По аналогии строим эпюру давления нефти справа. Эпюра давления также представляет нагрузку в виде треугольной призмы.

Стрелками покажем направление действия нефти на вертикальную проекцию справа налево.

Рассчитаем силу



Покажем линию действия силы . Сила проходит через центр тяжести второй эпюры на глубине и направлена по нормали к вертикальной проекции справа налево (рис. 19,б).

Определим горизонтальную составляющую R_x путём геометрического сложения составляющих и :





Положение силы определим, пользуясь теоремой Вариньона: момент от равнодействующей равен сумме моментов составляющих сил и относительно той же оси, например 0–0, совмещённой с дном.

Обозначим через y_D расстояние от оси 0–0, на котором приложена сила R_x(расстояние y_D обозначаем без учёта направления оси y):



На расстоянии y_D от дна покажем линию действия и точку приложения горизонтальной силы R_x (рис. 19,б).

Глубина погружения центра давления для горизонтальной составляющей равна h_D = H₁ – y_D = 1,2 – 0,47 = 0,73 м.

Сила R_x направлена по нормали слева направо на вертикальную проекцию криволинейной поверхности.

3. Определим величину, направление и точку приложения вертикальной составляющей R_y.

Согласно формулы имеем:

R_y = ρgV_{т. д}.

Найдём положение результирующего тела давления.

На рис. 19,в представлено построение тела давления для левой и правой частей криволинейной поверхности согласно принятой методике.

Для левой части получаем отрицательное тело давления в виде полуцилиндра (см. аналогию построения тела давления в задаче 14):



Для правой части тело давления положительное; объём тела – в виде четверти цилиндра:

При геометрическом сложении объёмов двух тел давления –положительного и отрицательного, т.е. при наложении объёмов тела давления, получим результирующее тело давления отрицательное в виде четверти цилиндра (рис. 19,б).

Вертикальная составляющая R_y равна:



Из центра тяжести результирующего тела давления, т.е. из центра тяжести цилиндра, направлена вверх вертикальная составляющая R_y.

Центр тяжести четверти цилиндра так же, как центр тяжести полу-цилиндра, находится на расстоянии (приложение, табл. 3):

x_c = 4r/3π;



На рис. 19,б покажем величинуx_c и положение вертикальной составляющей R_y.

4. Находим величину равнодействующей силы R:



Чтобы найти положение и точку приложения равнодействующей силы давления нефти R, продолжим составляющие силы R_x и R_yдо взаимного пересечения, получим точку N (рис. 19,б).

Вынесем точку N вне чертежа и проведём геометрическое сложение сил (см. аналогичные построения в задачах 13 и 14).

Равнодействующую силу R по линии действия перенесём параллельно в точкуN, т.е. в точку пересечения составляющих сил на основном чертеже и найдём точку пересечения силы R с криволинейной поверхностью.

Эта точка является центром давления для результирующей сил давления нефти.

Равнодействующая сила R должна быть направлена по радиусу к криволинейной поверхности. Действительно, сила R проходит через центр цилиндрической поверхности, т.е. построение верно.

Угол наклона равнодействующей найдём через tg α :



Ответ: сила давления нефти на цилиндрическую поверхность R = 21,5 кН, действует радиально под углом
В задачах представлены аналитический и графоаналитический методы определения горизонтальной составляющей силы давления жидкости на криволинейную поверхность, а также расчёт вертикальной составляющей силы через объём результирующего тела давления.

В этих задачах объём тела давления представлен простыми геометрическими фигурами, положение центра тяжести которых определяется по таблице.

На примере решения задачи 16 рассмотрим определение центра тяжести тела давления для сложной геометрической фигуры.
Задача 16.
Определить силу давления воды на четверть цилиндрической поверхности АВоткрытого резервуара, угол наклона силы к горизонту и глубину погружения центра давления, если глубина заполнения резервуара

Н= 1,6 м, радиус цилиндрической поверхности r = 0,8 м, длина резервуара

L = 5,0 м (рис. 20).

Решение.
На рис. 20,а дан общий вид резервуара с цилиндрической поверхностью в изометрии.

Согласно принятой методике, проводим следующие расчёты.

1. Выберем направления x и y, по которым определим составляющие силы давления с последующим их геометрическим сложением:



Начало координат выберем на свободной поверхности.

Ось x направим вправо по направлению действия жидкости, ось y – вертикально вниз.

2. Определим горизонтальную составляющую R_x по формуле:

R_x = ρgy_CA_y .

Спроектируем цилиндрическую поверхность AB на вертикальную плоскость. Получим в проекции прямоугольник высотой и шириной, равной длине резервуара L. Площадь вертикальной проекции четверти цилиндра A_y = rL.

Находим координату (глубину погружения) центра тяжести вертикальной проекции y_C, которая отсчитывается от свободной поверхности жидкости:



Покажем координату y_C на чертеже (рис. 20,б).

Рассчитаем горизонтальную составляющую силы R_x:





Покажем направление и точку приложения силыR_x.

Сила приложена в центре давления по нормали к вертикальной проекции на глубине y_D. По формуле определим:



где I_C – центральный момент инерции вертикальной проекции криволинейной поверхности относительно горизонтальной оси, т.е. момент инерции прямоугольника, который равен:



Подставим значения всех параметров:



Эксцентриситет е, т.е. понижение центра давления относительно центра тяжести вертикальной проекции равен:





На чертеже (рис. 20,б) покажем координату центра давления y_D, эксцентриситет е, направление и точку приложения силы R_x.

Сила направлена слева направо по направлению действия воды.

3. Определим вертикальную составляющую силы R_y по формуле:

R_y =ρgV_{т. д,}

т.е. вертикальная составляющая равна силе тяжести жидкости в объёме тела давления.

Чтобы найти объём тела давления, построим эпюру тела давления.
Из контура цилиндрической поверхности проведём вертикальные линии до продолжения свободной поверхности.

Тело давления ограничено самой криволинейной поверхностью АВ, вертикальными проектирующими плоскостями и горизонтальной проекцией криволинейной поверхности АВ на продолжение горизонта свободной поверхности.

Очерченное тело давления построено на несмоченной части криволинейной поверхности АВ, не заполнено жидкостью, поэтому оно считается отрицательным. Стрелки на эпюре тела давления направлены вверх (сила R_y будет также направлена вверх).

Тело давления представляет криволинейную призму с основанием А и высотой, равной L.

Площадь основания тела давления можно рассматривать как разность площадей двух геометрических фигур:

прямоугольника

и четверти круга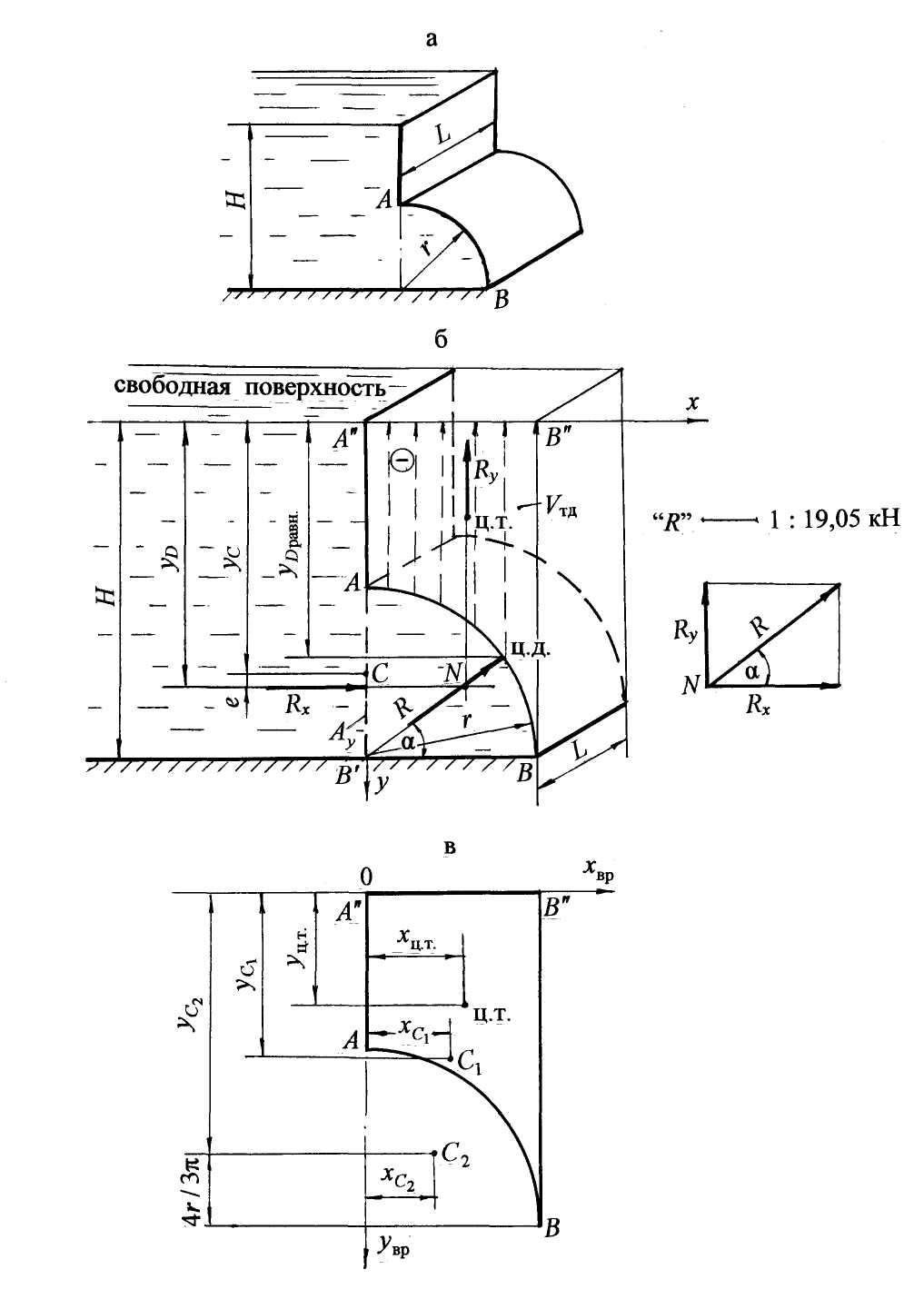



Рис. 20.


Тогда объём тела давления равен:

_.

Вертикальная составляющая R_y равна:





Переходим к определению направления и точки приложения вертикальной составляющей R_y.

Сила R_y из центра тяжести тела давления будет направлена вверх, т.к. тело давления отрицательное.

Нужно найти положение центра тяжести тела давления, т.е. центра тяжести основания тела давления А.

Положение центра тяжести составной фигуры определим, пользуясь понятием статического момента площади.

Согласно формулам, изучаемым в курсе сопротивления материалов, в данной задаче вычислим координаты центра тяжести сложной фигуры:



где S₁ – площадь прямоугольника ; S₂ – площадь четверти круга;

x₁ и x₂ ; y₁ и y₂ – координаты центров тяжести прямоугольника и четверти круга относительно временных осей x _вр , y _вр.

На рис. 20,в представлено основание тела давления

Временные оси x _вр и y _вр для удобства расчётов совпадают с направлением осей xи y на основном чертеже (рис.20,б).

Для расчёта координат центра тяжести x _{ц. т} и y _{ц. т} фигуры имеем:







Откладываем значения координат центра тяжести тела давления x_ц.т и y_ц.т на рис. 20,в.

В соответствующем масштабе переносим положение центра тяжести тела давления на основной чертёж (рис. 20,б); покажем линию действия и точку приложения вертикальной составляющей R_y.

Как было указано выше, эта сила приложена в центре тяжести тела давления и направлена вертикально вверх.

4. Определим величину равнодействующей сил давления воды R на цилиндрическую поверхность АВ по формуле:


Находим положение силыR.

Геометрически сложим составляющие силы R_x и R_y; для этого продолжаем силы по линии их действия до взаимного пересечения, получаем точку N, через которую пройдёт равнодействующая R.

Для удобства построения точку N вынесем за пределы чертежа и покажем сложение сил.

Чтобы найти положение центра давления для равнодействующей силы R, эту силу по линии действия параллельно перенесём в точку N на основной чертеж (рис. 20,б) и продолжим её до пересечения с криволинейной поверхностью АВ.

Итак, центр давления – это точка пересечения линии действия силы R с цилиндрической поверхностью АВ.

Равнодействующая сила R должна быть направлена по радиусу и проходить через точку N пересечения составляющих сил R_x и R_y , т.к. сила давления всегда действует по нормали или радиально к поверхности.

Проверим построение в масштабе. Построение верно.

Определим угол α наклона равнодействующей к горизонту через tg α:



Глубину погружения центра давления для равнодействующей силы R рассчитаем по формуле:



Покажем глубину погружения центра давления для равнодействующей ( ) на основном чертеже (рис. 20,б).

Ответ: сила давления воды на цилиндрическую поверхность R = 60,5 кН радиально направлена под углом α = 39˚, приложена на глубине


Рассмотрим случай определения силы давления жидкости на криволинейную поверхность в виде полусферы на примере решения задачи 17.

Задача 17.
Определить силу давления бензина на полусферическую крышку закрытого резервуара (рис. 21).

На поверхности бензина действует избыточное давление паров бензина р_ман = 0,03 ат. Крышка перекрывает круглое донное отверстие радиусом r = 0,3 м. Глубина заполнения резервуара Н = 0,9 м. Принять плотность бензина ρ_бенз = 750 кг/м³.


Решение.
На рис. 21,а представлен общий вид резервуара с бензином в вертикальном разрезе.

Прежде чем приступать к решению задачи, следует определиться с методикой учёта избыточного давления на поверхности бензина при расчёте силы давления на полусферическую поверхность.
Здесь могут быть выбраны два варианта.

Во-первых, рассчитать отдельно составляющую силу от внешнего, манометрического давления, а затем суммировать её с силой давления жидкости и найти равнодействующую сил давления.

Во-вторых, манометрическое давление на поверхности жидкости можно перевести в давление столба бензина, условно заменив манометр пьезометром, найти пьезометрическую высоту и положение условной свободнойповерхности.

Такая методика расчёта рассмотрена в задачах 11; 12; 13. Эта методика расчёта позволит сразу определить равнодействующую сил давления жидкости и манометрического давления.

Выберем второй вариант решения.

Рассчитаем пьезометрический напор по показанию манометра, пользуясь формулой:



На уровне свободной поверхности в резервуаре (рис. 21, б) пунктиром покажем пьезометр, высота столба жидкости в котором соответствует .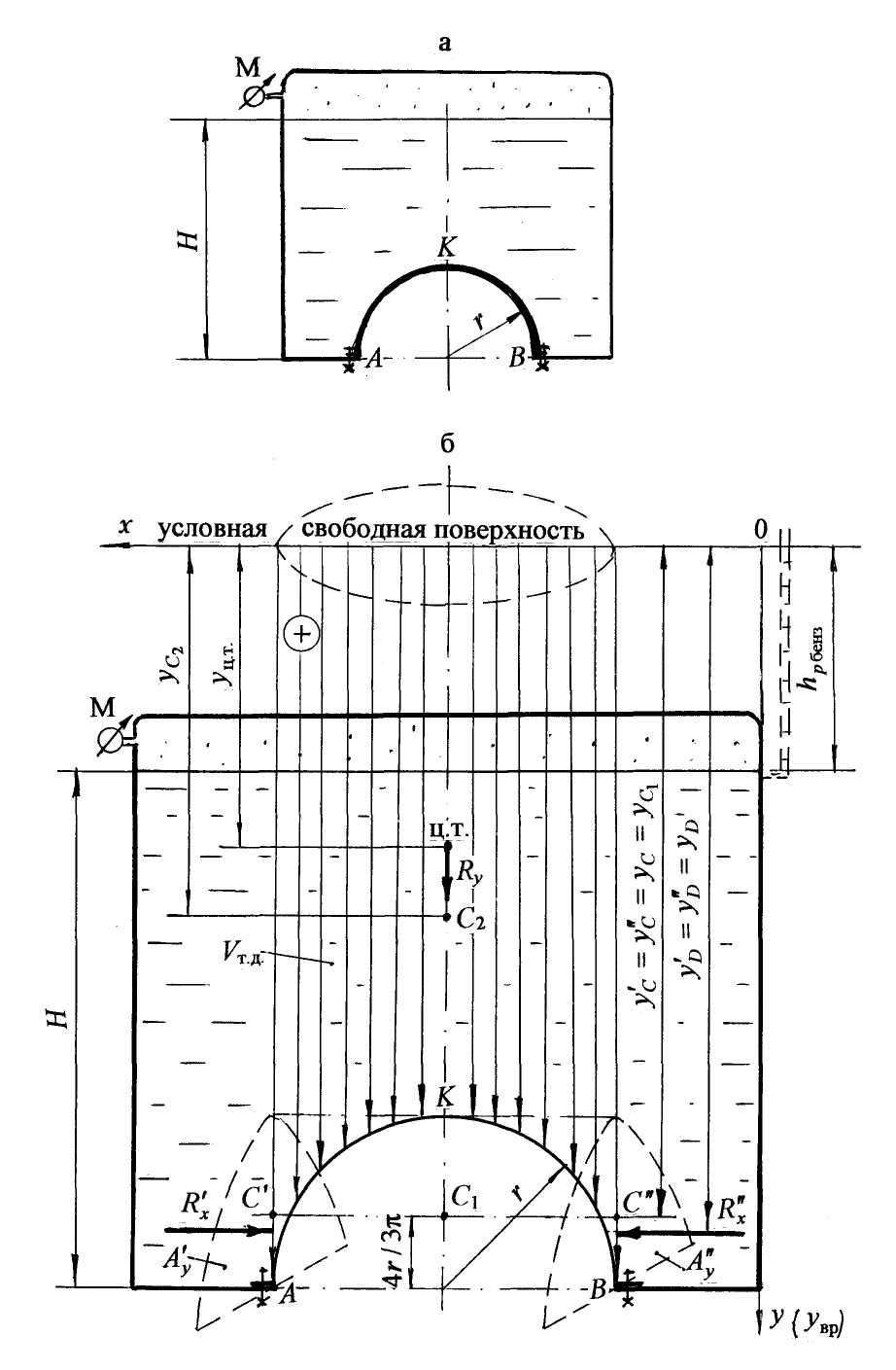



Рис. 21


По уровню жидкости в пьезометре покажем условную свободную поверхность, от которой будем отсчитывать координаты центров тяжести фигур и центра давления.

Дальнейший расчёт силы давления бензина на полусферическую поверхность проводим по принятой методике:

1. Выберем два направления – x и y (рис. 21,б), по которым определим составляющие силы давления с последующим их геометрическим сложением.

2. Определим горизонтальную составляющую R_x по формуле:

R_x= ρ _бенз gy_CA_y.

Полусферическая поверхность АКВ имеет две части: часть АК – с действием бензина слева и часть КВ – с действием бензина справа.

Чтобы определить горизонтальную силу на левую часть полусферы, спроектируем часть АК в жидкость на вертикальную плоскость.

В проекции получим полукруг площадью .

Проекция показана пунктирными линиями.
Затем спроектируем правую часть полусферы в жидкости и получим точно такую же проекцию в виде полукруга площадью

.

Находим координаты центров тяжести этих проекций:

.

Покажем координаты центров тяжести проекций на чертеже (рис. 21,б).

Получим формулы для горизонтальных сил слева и справа:





Силы и равны по величине, но противоположно направлены.

Поскольку координаты центров тяжести проекций равны, то равны и координаты центров давления слева и справа:

На глубине y_D покажем силы и , которые противоположно направлены.

Таким образом, при геометрическом сложении сил и получим:



Горизонтальная составляющая силы давления жидкости на полусферическую поверхность равна нулю.

3. Определим вертикальную составляющую силы давления на полусферическую поверхность R_y по формуле: R_y = ρ_бенз g V_т.д .

Чтобы построить тело давления, из контура полусферы проведём вертикальные линии до условной свободной поверхности.

Получим эпюру тела давления. Тело давления построено на смоченной части полусферы, заполнено жидкостью, значит, оно действительное или положительное.

Стрелками, направленными вниз, покажем действие бензина на полусферическую крышку (сила R_y также будет направлена вниз).

Горизонтальная проекция полусферы на условную свободную поверхность представляет круг.

Таким образом, объём тела давления – это объём цилиндра высотой равной , за вычетом объёма полусферы:

;

.

Вертикальная составляющая R_y:





Линия действия силы совпадает с геометрической осью полусферической поверхности и цилиндра.

Необязательно находить точку приложения силы R_y, т.к. силу по линии действия можно перемещать.

В соответствии с методикой расчёта определим положение центра тяжести тела давления.

Требуется определить координату центра тяжести тела давления y_ц.т, т.е. центра тяжести геометрической фигуры, представляющей вертикальное сечение закрытого резервуара (см. расчёт в задаче 16).

По уровню жидкости в пьезометре покажем условную свободную поверхность, от которой будем отсчитывать координаты центров тяжести фигур и центра давления.

Дальнейший расчёт силы давления бензина на полусферическую поверхность проводим по принятой методике:

1. Выберем два направления – x и y (рис. 21,б), по которым определим составляющие силы давления с последующим их геометрическим сложением.

2. Определим горизонтальную составляющую R_x по формуле:

R_x= ρ _бенз gy_CA_y.

Полусферическая поверхность АКВ имеет две части: часть АК – с действием бензина слева и часть КВ – с действием бензина справа.

Чтобы определить горизонтальную силу на левую часть полусферы, спроектируем часть АК в жидкость на вертикальную плоскость.

В проекции получим полукруг площадью .

Проекция показана пунктирными линиями.
Затем спроектируем правую часть полусферы в жидкости и получим точно такую же проекцию в виде полукруга площадью

.

Находим координаты центров тяжести этих проекций:

.

Покажем координаты центров тяжести проекций на чертеже (рис. 21,б).

Получим формулы для горизонтальных сил слева и справа:





Силы и равны по величине, но противоположно направлены.

Поскольку координаты центров тяжести проекций равны, то равны и координаты центров давления слева и справа:

На глубине y_D покажем силы и , которые противоположно направлены.

Таким образом, при геометрическом сложении сил и получим:



Горизонтальная составляющая силы давления жидкости на полусферическую поверхность равна нулю.

3. Определим вертикальную составляющую силы давления на полусферическую поверхность R_y по формуле:

R_y = ρ_бенз g V_т.д .

Чтобы построить тело давления, из контура полусферы проведём вертикальные линии до условной свободной поверхности.

Получим эпюру тела давления. Тело давления построено на смоченной части полусферы, заполнено жидкостью, значит, оно действительное или положительное.

Стрелками, направленными вниз, покажем действие бензина на полусферическую крышку (сила R_y также будет направлена вниз).

Горизонтальная проекция полусферы на условную свободную поверхность представляет круг.

Таким образом, объём тела давления – это объём цилиндра высотой равной , за вычетом объёма полусферы:

;

.

Вертикальная составляющая R_y:





Следует показать линию действия и точку приложения вертикальной силы R_y. Линия действия силы совпадает с геометрической осью полусферической поверхности и цилиндра. Необязательно находить точку приложения силы R_y, т.к. силу по линии действия можно перемещать.

В соответствии с методикой расчёта определим положение центра тяжести тела давления.

Требуется определить координату центра тяжести тела давления y_ц.т, т.е. центра тяжести геометрической фигуры, представляющей вертикальное сечение закрытого резервуара (см. расчёт в задаче 16).

Покажем линию действия и точку приложения вертикальной силы R_y.

Временную ось y _вр совместим с осью y, тогда

,

где – площадь полукруга (вертикальное сечение полусферы);

– площадь прямоугольника;

– координата центра тяжести С₁полукруга

(рис.1.30,б);

– координата центра тяжести С₂ прямоугольника.

Для расчётов принимаем:



Получим y_ц.т = 0,54 м.

Покажем на чертеже y_ц.т и положение центра тяжести тела давления (ц.т.).

Из центра тяжести тела давления вертикальную силу R_y направим вниз. Поскольку горизонтальная сила давления равна нулю (R_x = 0), то на полусферическую поверхность действует только вертикальная сила, и равнодействующая сила R= R_y.
Ответ: на полусферическую крышку резервуара по оси полусферы действует сила R= R_y =2,29 кН.
Во всех приведённых выше примерах по определению силы давления на криволинейную поверхность учитывалось давление жидкости, а также избыточное давление по показанию манометра р_ман..

В практике расчётов силы давления на криволинейную поверхность может быть условие, когда на поверхности жидкости или на определённом уровне в закрытом резервуаре известно вакуумметрическое давление р_вак..

Рассмотрим пример решения задачи с учётом вакуумметрического давления р_вак по показанию вакуумметра В.
Задача18.
В закрытом резервуаре, заполненном водой, в боковой плоской стенке сделано отверстие, которое перекрывается полусферической крышкой радиусом r = 0,6 м (рис. 22).

Крышка укреплена с помощью шарнира в точке А.

На расстоянии h =1,4 м от шарнира установлен вакуумметр В, показание которого р_вак = 0,05 ат.

Определить силу F для удержания крышки в закрытом положении. Принять плотность воды ρ = 10³ кг/м³.

На рис. 22,а представлен общий вид закрытого резервуара.

Прежде чем приступить к решению задачи, следует произвести предварительные расчёты, а именно: определить вакуумметрический напор h_вак, соответствующий показанию вакуумметра:

;



Вакуумметрический напор меньше напора жидкости hна уровне шарнира А равен: h_вак < h.

Это значит, что можно выбрать рациональный метод решения, т.е. вывести пьезометр на любом удобном уровне, например по оси полусферы, показать h_вак и условную свободную поверхность (рис. 22,б).

Вакуумметрический напор (h_вак), как отрицательная величина, откладывается вниз от уровня установки вакуумметра.

Решение.
Воспользуемся теоретическими положениями и методикой расчёта сил давления на криволинейную поверхность.

1. Выберем два направления x и y, по которым определим горизонтальную и вертикальную силы давления.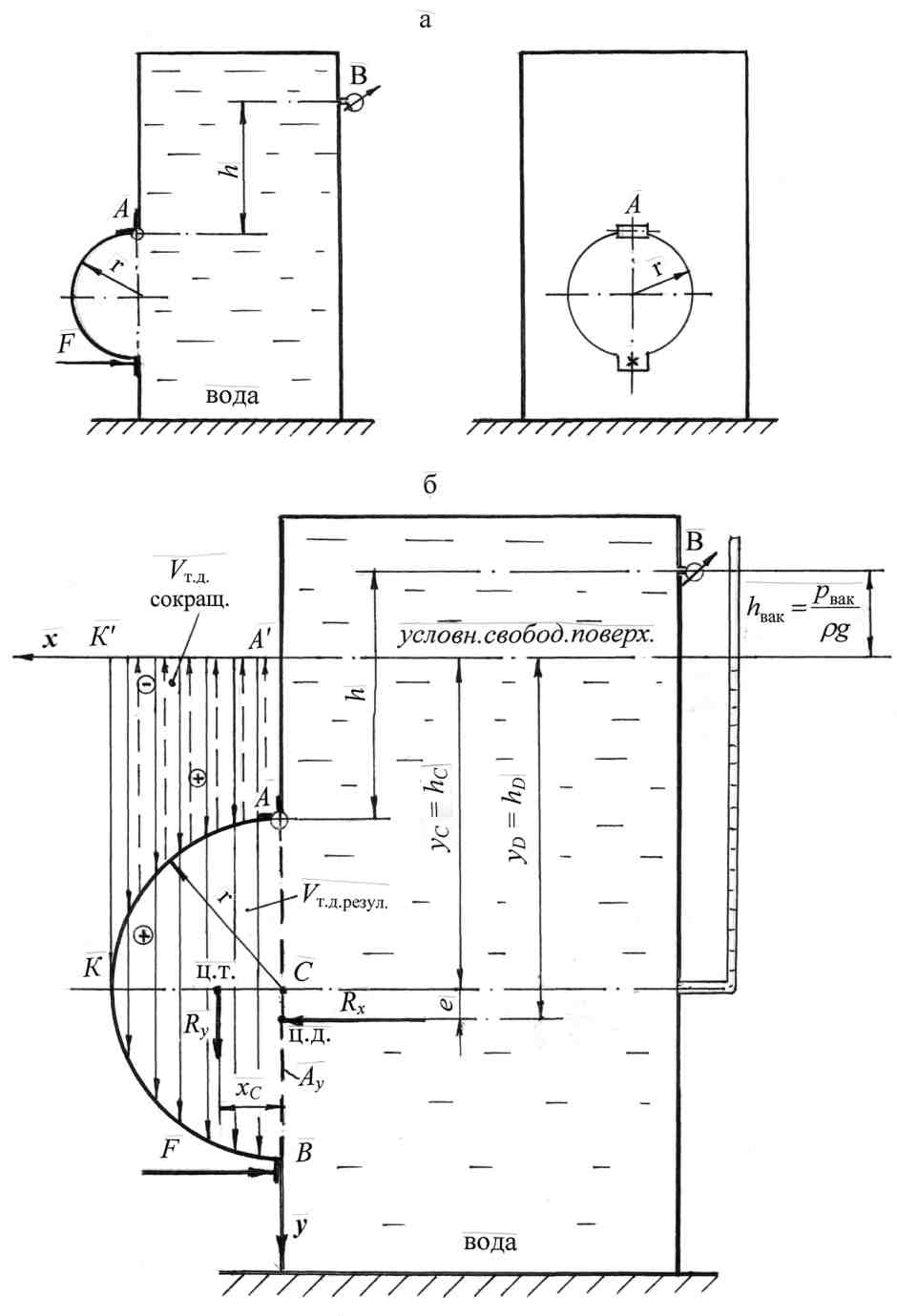


Рис. 22

Ось x проведём по условной свободной поверхности справа налево по направлению действия жидкости, ось y проведем вертикально вниз

(рис. 22,б).

2. Рассчитаем горизонтальную силу давления R_x. Спроектируем полусферу на вертикальную плоскость. Вертикальная проекция полусферы представляет собой круг ( пунктирная линия на рис. 22,б).

Согласно формуле:

R_x = ρgy_CA_y .

Можно считать координату центра тяжести вертикальной проекции y_C, равной глубине погружения центра тяжести круга h_С, отсчитанной от условной свободной поверхности:

y_C = h_С.
ТогдаR_x = ρgh_CA_y,

где h_С = h – h_вак + r ; h_С = 1,4 – 0,5 + 0,6 = 1,5 м;

A_y – площадь вертикальной проекции криволинейной поверхности

A_y= πr²; A_y = 3,14·0,6² = 1,13 м²;

R_x = ρg(h – h_вак + r) πr²;

R_x = 10³·9,8·1,5·1,13 = 16,61·10³ Н = 16,61 кН.

Определяем линию действия, направление и глубину точки приложения горизонтальной силы R_x.

Сила направлена из жидкости на вертикальную проекцию и приложена в центре давления на глубине, равной

h_D = y_D



где I_C – центральный момент инерции вертикальной проекции (круга) относительно горизонтальной оси:

; ; h_D = 1,5 + 0,1 = 1,6 м;

эксцентриситет м.

Покажем на рис. 22,б эксцентриситет е, глубину погружения центра давления h_D и горизонтальную силу давления R_x.
3. Рассчитаем вертикальную силу R_y по формуле:

R_y = ρgV_{т. д}.

Определим объём тела давления V_{т. д}.

Из контура верхней части полусферы АК проведём вертикальные линии до условной свободной поверхности, получим криволинейный объём с основанием АА′К′КА в вертикальном сечении (рис. 22,б).

Т.к. тело давления построено на несмоченной части криволинейной поверхности и не заполнено жидкостью, то оно считается отрицательным (пунктирные линии, стрелки направлены вверх).

При аналогичных построениях для нижней части полусферы получим тело давления с основанием ВКК′А′В.

Если тело давления построено на смоченной части криволинейной поверхности и заполнено жидкостью, то оно считается положительным. Эпюра тела давления заштрихована стрелками, направленными вниз (рис. 22,б).

В объёме АА′К′КА два объёма тел давления сокращаются (взаимно уничтожаются).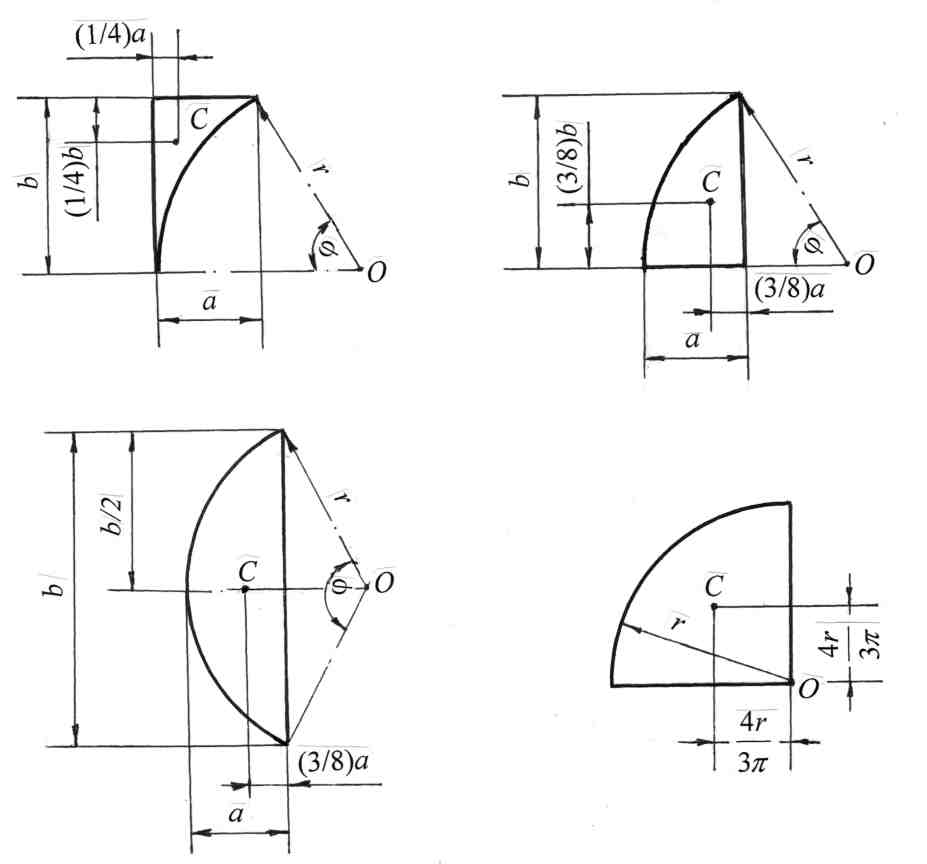



Результирующий объём тела давления получается положительным в виде полусферы: V_{т. д. резул} = V_полусф = .

Вертикальная сила давления R_y:

R_y = ρg ; R_y = 4,43·10³ Н = 4,43 кН.

Сила R_y направлена вертикально вниз, приложена в центре тяжести полусферы на расстоянии (табл. 3, приложение): ; x_C = 0,25 м.

Покажем на рис. 22,б координату центра тяжести (ц.т.) полусферы x_C и вертикальную силу R_y.

По условию задачи не требуется определять результирующую от сил давления и её положение.

4. Рассчитаем силу F для удержания полусферической крышки в закрытом положении.

Воспользуемся уравнением механики: сумма моментов относительно шарнира А равна нулю: ΣМ_А = 0; F·2r+ R_y· x_C – R_x (r +e) = 0;

;

кН.
Ответ: для удержания полусферической крышки в закрытом положении необходимо приложить силу F кН.