ПРимеры практических. 1,2 Очники Примеры практ.. "Гидростатическое давление в жидкости"

• Название: "Гидростатическое давление в жидкости"
• Анкор: ПРимеры практических
• Дата: 07.05.2022
• Размер: 2.89 Mb.
• Имя файла: 1,2 Очники Примеры практ..doc
• Тип: Задача; #516168
• страница: 6 из 8

Пример решения задачи по теме:

“Расчёт простых трубопроводных систем”

Задача 19.
С помощью насоса по трубе диаметром d= 50 мм и длиной l = 70 м нефть подаётся в закрытый резервуар на высоту Н = 15 м.

Считать H = const (рис. 23).

Определить показание мановакуумметра (рмв), установленного на поверхности нефти в закрытом резервуаре, если показание манометра после насоса равно рман = 1,3 ат.

Расход нефти Q = 1,2 л/c, плотность нефти ρн = 900 кг/м3, относительная вязкость по Энглеру ˚Е=4,0. В системе установлен пробковый кран с коэффициентом сопротивления ζ_кр = 17,4 и два колена с коэффициентом сопротивления ζ_кол = 0,8 (рис. 23).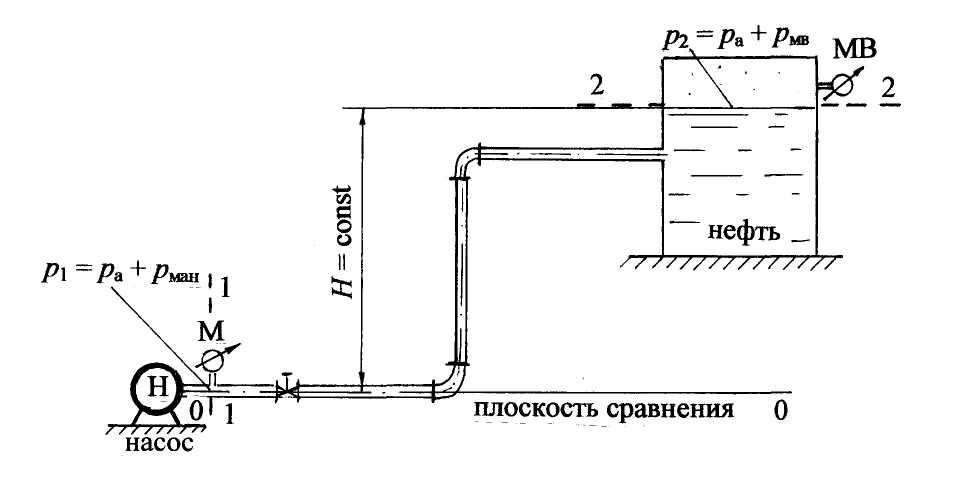



Рис. 23
Решение.
Представленная трубопроводная система относится к первому типу простых систем.

Напомним, что мановакуумметр – это прибор, который может измерять как манометрическое (избыточное) давление, так и вакуум.

При решении задачи давление на поверхности нефти обозначим р_мв. Если при решении задачи давление получится положительным, значит, мановакуумметр работает как манометр; отрицательное значение давления показывает, что мановакуумметр работает как вакуумметр.

Для определения показания мановакуумметра воспользуемся уравнением Бернулли.

Применим методику по составлению уравнения.

1. Выбираем два сечения:

одно сечение – в месте установки манометра; это сечение проводим перпендикулярно к направлению движения жидкости, где скорость равна скорости движения нефти в трубе υ;

другое сечение – по свободной поверхности в резервуаре, где давление определяется по мановакуумметру, а скорость равна нулю.

2. Сечения 1–1 и 2–2 нумеруем по направлению движения жидкости так, чтобы в уравнении потери напора в гидравлических сопротивлениях учитывались со знаком «плюс».

3. В выбранных сечениях принимаем абсолютное давление (с учётом атмосферного): р₁ = р_а + р_ман; р₂ = р_а + р_мв.

4. Плоскость сравнения 0–0 проводим через ось первого сечения:

z₁ = 0; z₂ = H.

5. Записываем уравнение Бернулли в общем виде и производим подстановку всех параметров:

;

z₁ = 0; z₂ = H;

p₁ = p_а + р_ман; р₂ = р_а + р_мв;

υ_{1 сеч} = υ; α₁ = 2,0; υ_{2 сеч} = 0.
Движущаяся жидкость – нефть относится к вязким жидкостям, поэтому предполагаем ламинарный режим (коэффициент α₁ = 2,0).

В процессе решения задачи режим движения нефти будет проверен.

Подставляем все параметры в уравнение Бернулли:

.

После сокращений и преобразования уравнения Бернулли получим:

.

Рассчитаем все слагаемые в уравнении:

.

Скорость движения нефти в трубе υ рассчитываем через расход Q:

;

расход Qи диаметр d равны:

Q= 1,2 л/с = 1,2 · 10^-3 м³/с; d= 0,05 м; ;

скоростной напор равен: (малая величина).

Рассчитаем потери напора в гидравлических сопротивлениях по формуле:

h_w = Σh_r + h_l ;

потери напора в местных сопротивлениях по формуле:

,

где Σζ – сумма коэффициентов местных сопротивлений.
Учитываем потери напора в двух коленах и в пробковом кране:

Σ_ζ = 2 ζ_кол + ζ_кр + ζ_вых ;

по табл. принимаем:

ζ_кр = 17,3 при угле закрытия α = 40˚, ζ_вых =1,0;

тогда: Σζ = 2 · 0,8 + 17,4 + 1,0 = 20,0;

получим: Σh_r= 20,0 · 0,019 = 0,38 м.

Потери напора по длине определяем согласно формуле:

.

Для выбора расчётной формулы коэффициента гидравлического сопротивления λ (рис. 23) определим режим движения жидкости по критерию Рейнольдса: .

В эту формулу входит коэффициент кинематической вязкости ν.

Для расчёта этого коэффициента воспользуемся значением относительной вязкости в градусах Энглера (˚Е) (см. физические свойства жидкости). По формуле Уббелоде:

;

; ν = 0,277·10^-4 м²/c.

Получим: .

Т.к. число Re меньше критического значения, следовательно, имеет место ламинарный режим движения нефти.

Принятое значение коэффициента α₁ = 2,0 верно.

Для ламинарного режима коэффициент гидравлического сопротив-ления λ рассчитывается по формуле:

.

Рассчитаем потери напора по длине:

; .

Потери напора в гидравлических сопротивлениях:

h_w = 0,38 + 1,54 = 1,92 м.

Подставим значение всех слагаемых в преобразованное уравнение Бернулли (3.10): .

Получили отрицательное значение, значит, мановакуумметр работает как вакуумметр.

Величина вакуума равна:

р_вак = 2,44 · ρ_н g = 2,44·900·9,8 = 21521 Па или р_вак = 0,22 ат.
Ответ. Показание мановакуумметра соответствует вакуумметри-ческому давлению: р_мв = р_вак = 0,22 ат.