Разработка мехатронной аддитивной установки для изготовления песчаных и гипсовых литейных форм и исследования путей повышения то. ШАШКОВ_ДИПЛОМ. Государственное бюджетное профессиональное образовательное учреждение московский государственный образовательный комплекс
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
|
Размер частиц, мкм Форму песчинок 1K1O101 исследовали с помощью оптического микроскопа (рис. 2.4.9). Как упоминалось выше, увеличение угловатости и отклонения сферичности частиц песка снижает плотность заряда частицы. Вышеуказанные параметры порошковой системы из кварцевого песка влияют на плотность упаковки и, следовательно, на отклонение фактических размеров от номинальных.  Рисунок 2.4.9 – Частицы кварцевого песка. Описание метода решения задачи исследования структуры стопки частиц. Для моделирования случайной структуры упаковки порошковых систем используются следующие методы: 1. Алгоритм «сжатия» Любачевского-Стиллингера; 2. Алгоритм "отталкивания" Жодре-Тори; 3. Алгоритм прокатки частиц по методу «drop-and-roll»; 4. Метод дискретных элементов. Наиболее интересен метод дискретных элементов как преимущественно дискретный метод, основанный на применении законов Ньютона и контактной механики. В непрерывных моделях нет недостатков, которые могли бы возникнуть, когда материя непрерывна или когда внутренняя структура дискретна. Высокая эффективность этого метода обусловлена его универсальностью по сравнению с относительно невысокой стоимостью компьютерных экспериментов, естественными и практически неограниченными возможностями диагностики моделируемых явлений. Гранулированный материал представляет собой набор из N изолированных сферических упругих частиц с радиусом Ri (рисунок 2.4.10.a). Согласно законам классической механики Ньютона, движение каждой i-й частицы полностью определяется координатами ее центра тяжести xi и углом поворота Ri вокруг центра тяжести как твердого тела (i = 1,. .., N). Система уравнений движения для каждого элемента в прямоугольной декартовой системе координат выглядит следующим образом 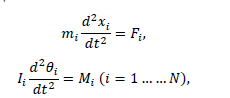 Здесь t - время, mi - масса частицы, Ii - момент инерции, векторы Fi - сумма сил, действующих на контакты i-й и j-й частиц (включая гравитацию): 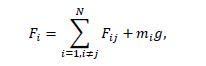 Вектор Mi - это момент сил Fij относительно центра i-й частицы: Поверхностные силы Fij состоят из сил отталкивания Fn, ij и сил трения Fi. Сила отталкивания возникает между частицами при условии δi> 0 (рисунок 2.4.10.a) и направлена по нормали nij к центру i-й частицы (рисунок 2.4.10.б). Чтобы определить это, мы выбрали вязкоупругую модель столкновения: 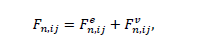  Согласно Дж. Герцу, упругая часть силы Fn,ij равна 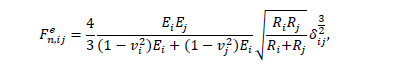 где vi –Пуассонов коэффициент, Ei – Модуль упругости частиц. Если частица сталкивается с прямой границей, достаточно установить один из радиусов в формуле равным бесконечности. 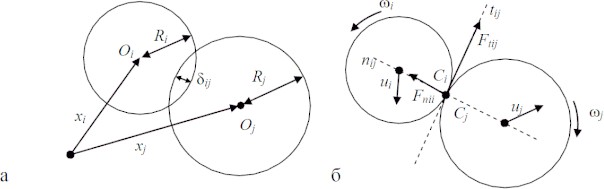 Рисунок 2.4.10 – При настройке параметров для описания контакта δij - степень перекрытия частиц: геометрия модели (а); Силы, действующие при контакте (б) Вязкая составляющая силы отталкивания определяется из соотношения: где Mij - приведенная масса частиц, un, ij - проекция относительной скорости Точки удара на оси nij, γn представляют собой коэффициент демпфирования, который имеет большое влияние на коэффициент восстановления скорости после удара. Сила трения Ft, ij направлена против движения i-й частицы относительно j-й частицы, и ее величина определяется соотношением: где ut,ij – проекция скорости точки контакта Ci относительно скорости точки Cj на оси tij, φt - угол контактного трения между частицами. Таким образом, система дифференциальных уравнений второго порядка (1-2) для неизвестных xi, θi и соотношений (3-7) полностью определяет движение и столкновение набора упругих частиц, моделирующих дискретную среду. Одной из самых известных методических программ для дискретных элементов является программа EDEM от DEM Solution.  Структурное моделирование выбранного самотечного резервуара 9 мм3 было выполнено без уплотнения другими способами, такими как вибрация. Размер емкости был выбран по двум критериям: статистическая достоверность результата и минимальное время, затрачиваемое на расчет с доступными вычислительными средствами (разумное время расчета на персональном компьютере). Процесс моделирования занял 59 часов в реальном времени. Во время моделирования было сгенерировано 2096 сферических частиц с соответствующим гранулометрическим составом отобранного образца песка 1K1O101. Окончательный результат моделирования пучка частиц показан на рисунке 2.4.11. Физико-механические параметры частиц приведены в таблице 2.4.1 Структурное моделирование выбранного самотечного резервуара 9 мм3 было выполнено без уплотнения другими способами, такими как вибрация. Размер емкости был выбран по двум критериям: статистическая достоверность результата и минимальное время, затрачиваемое на расчет с доступными вычислительными средствами (разумное время расчета на персональном компьютере). Процесс моделирования занял 59 часов в реальном времени. Во время моделирования было сгенерировано 2096 сферических частиц с соответствующим гранулометрическим составом отобранного образца песка 1K1O101. Окончательный результат моделирования пучка частиц показан на рисунке 2.4.11. Физико-механические параметры частиц приведены в таблице 2.4.1 Рисунок 2.4.11 – Результат моделирования упаковки частиц методом дискретных Рисунок 2.4.11 – Результат моделирования упаковки частиц методом дискретныхэлементов. Таблица 2.4.1. – Параметры песка, использованные при моделировании.
В результате моделирования объем частиц, заполнивших контейнер, составил 5,27 мм3, что составляет 58,5% от насыпной плотности и 1550 кг / м3. По экспериментальным данным фактическая насыпная плотность составляет 56,6% или 1500 кг / м3. Следовательно, ошибка моделирования составляет 1,9%. Показанная ошибка связана с тем, что фактическая форма частиц отличается от сферической формы. Математическая модель практически полностью соответствует экспериментальной и поэтому позволяет с большой достоверностью анализировать влияние гранулометрического состава песка на точность получаемого продукта. Для определения отклонения линейного размера от номинального использовалась встроенная программа EDEM. На фиг. 2.4.12 показывает естественное перекрытие частиц линиями номинального размера. После использования режущего инструмента эти линии удаляли частицы, центры которых находились за пределами указанного диапазона и, следовательно, имели слабую связь с частицами продукта. Это создало границу продукта (рис. 2.4.13), состоящую из частиц, которые имеют достаточно большое количество контактов и образуют прочную связь. 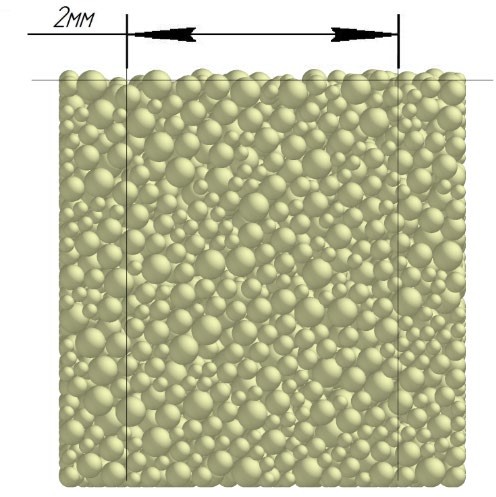 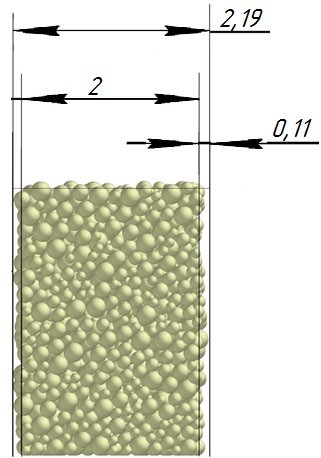 Рисунок 2.4.12 – Естественная упаковка частиц по номинальным размерам продукта. Рисунок 2.4.12 – Естественная упаковка частиц по номинальным размерам продукта.Рисунок 2.4.13 – Разница между фактическим размером и номиналом. Максимальное отклонение от номинального размера составило + 0,19 мм, максимальное отклонение в сторону составило 0,11 мм или половину максимального диаметра частиц в исследуемой дисперсной системе. В этом случае отклонение не зависит от номинального значения крупности, а определяется только гранулометрическим составом используемой в технологии дисперсной системы. Это означает, что при производстве деталей необходимо правильно выбирать соотношение сырья в зависимости от габаритов изделий и требуемой точности. Например, для изделия размером 500 х 500 х 200 мм и при использовании описанной выше тонкой системы отклонения составляют 9 баллов, что для данной технологии является достаточно высоким показателем. 2.5. Расчет параметров мехатронной составляющей установки. Рассчёт гидравлического привода. 2.5.1. Выбор обобщенных параметров привода. Все правила для систем управления перечислены выше. Динамика пневмодвигатея на момент загрузки Мн определяются двумя обобщенными параметрами: максимальной угловой скоростью 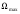 и величина безразмерной нагрузки и величина безразмерной нагрузки 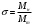 , где , где 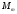 максимальный тормозной момент. Безразмерная нагрузка определяется с использованием критерия минимально необходимого расхода путем решения следующего уравнения: максимальный тормозной момент. Безразмерная нагрузка определяется с использованием критерия минимально необходимого расхода путем решения следующего уравнения: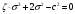 , ,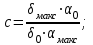 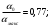 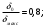 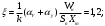 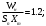 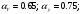 Получим 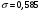 . .Следовательно, 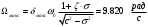 . .Найдём моменты нагрузки для конкретных моментов в шарнирах и максимального тормозного момента. 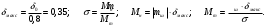 для силы пружины: 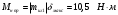 для нагрузки на опрокидывание: 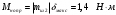 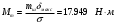 Согласно приведенной выше зависимости, поскольку значение максимальной угловой скорости определялось без учета трения, проанализируем ее с помощью коэффициента трения: 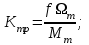 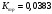 . .Фактическая максимальная угловая скорость с полученными обобщенными параметрами приведена ниже, мы учитываем это при пересчете 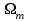 через зависимость: через зависимость: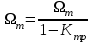 , ,Получаем 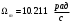 . .С учетом эффекта трения требуемая максимальная скорость увеличивается. 2.5.2 Расчет параметров контура при отрицательном крутящем моменте (усилие пружины) Обычная нагрузка, действующая на выходной вал пневматического двигателя, отличается тем, что она изменяется не только по размеру, но и по характеру во время работы. Поэтому в проектной документации указаны два конкретных момента подвески вместе с предельными значениями для отрицательной (пружина) и положительной (сверхкомпенсированной) нагрузок. Расчет ведется для наихудшего режима работы, т.е., для максимального момента нагрузки. Таким образом, схема разработана в соответствии с частотной характеристикой пружинного инвертора, и громкоговоритель испытывается в двух режимах. Если крутящий момент шарнира отрицательный, динамика пневмодвигателя описывается структурной схемой, показанной на рисунке 2.5.1. Для этой блок-схемы мы находим константы, соответствующие вышеупомянутым общим параметрам привода, а также параметрам процесса. система. ( 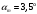 ). ).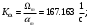 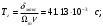 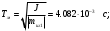 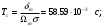 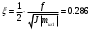 . .Для блок-схемы конструкции записываем частотные характеристики. С этой целью мы создадим ЛАЧХ для передаточной функции.: 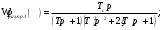 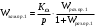 . .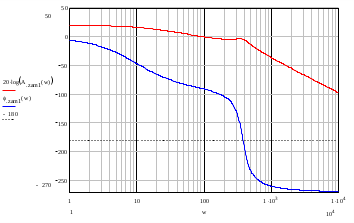 Рис.2.5.1. Частотные характеристики пневмопривода с отрицательным моментом. 2.5.3. Расчет параметров конструкции аддитивной установки Необходимо определить площадь механического преобразователя 1, динамометра и силового цилиндра 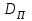 , величина свободного хода привода. При определении заплечика l необходимо определить отношение свободного хода поршня к его диаметру. , величина свободного хода привода. При определении заплечика l необходимо определить отношение свободного хода поршня к его диаметру.Благодаря компактности разработанной конструкции силового цилиндра передаточное отношение было: 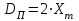 . .При перемещении 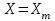 максимальный крутящий момент, создаваемый приводом, должен быть в максимальный крутящий момент, создаваемый приводом, должен быть в 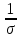 кратный максимальному крутящему моменту: кратный максимальному крутящему моменту: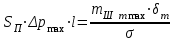 . .Учитывая принятое соотношение 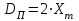 получаем зависимость из последнего равенства: получаем зависимость из последнего равенства: 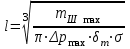 . .Максимальный перепад давления в полостях силового цилиндра это зависит от величины 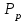 , характер и соотношение геометрических размеров ГРУ, а также интенсивность теплообмена в полостях. При расчете значения можно приблизительно принять для приводов с соплово-демпферным типом ГРУ , характер и соотношение геометрических размеров ГРУ, а также интенсивность теплообмена в полостях. При расчете значения можно приблизительно принять для приводов с соплово-демпферным типом ГРУ 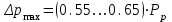 . .При расчете величины 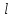 величина величина 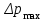 должен соответствовать 1-му режиму работы преобразователя частоты. Если выполнить все расчеты для вышеуказанных зависимостей, мы получим следующие результаты: должен соответствовать 1-му режиму работы преобразователя частоты. Если выполнить все расчеты для вышеуказанных зависимостей, мы получим следующие результаты: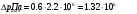 ; ; 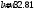 . .Для относительно малых значений угла 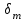 : :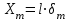 ; ; 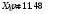 ; ;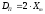 ; ; 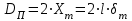 ; ; 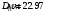 . .Определите объем рабочей полости с учетом предположений, сделанных ранее: 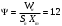 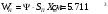 . .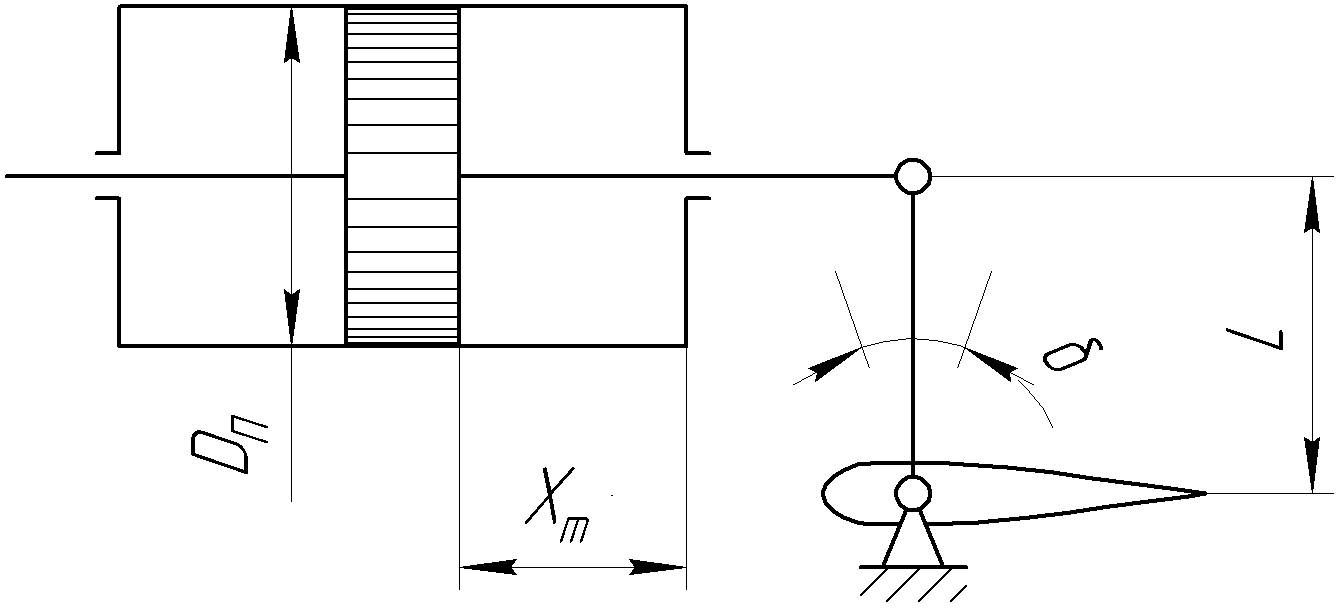 Рис. 2.5.2. |
