Графический метод в комбинации с методом замены переменной при решении уравнений

• Название: Графический метод в комбинации с методом замены переменной при решении уравнений
• Дата: 22.03.2022
• Размер: 0.59 Mb.
• Имя файла: elibrary_36981064_70105874.doc
• Тип: Документы; #409509
• страница: 4 из 4

Решение. Для подстановки используем гиперболические функции. Как известно, они определя- ются следующим образом: гиперболический синус

sh x :=

_ex _{− e}−x



2

и гиперболический косинус
Эти функции удовлетворяют тождеству
ch x :=
_ex _{+ e}−x



.

2

ch² x − sh² x = 1.

Сделаем подстановку x = sh y. Уравнение приводится к системе

�
x = sh y, e^x= sh y+

^J1+ sh² y.

Правая часть второго уравнения преобразуется к виду





sh y + ✓1+ sh² y = sh y + ✓ch² y = sh y + ch y = e^y.


≥

≥
Получаем уравнение e^x= e^y, откуда x = y. Тогда из первого уравнения получаем y = sh y. Оно имеет решение y = 0. Других решений нет. Для обоснования этого используем графическое представление. Аргументом считаем переменную y, функцией x. Графики функций x= yи x= sh y касаются в начале координат. Первый график — прямая, второй при y 0 — кривая, выпуклая вниз. Следовательно, других точек пересечения при y 0 нет. При y < 0 симметричная картина в силу нечетности функций. Следовательно, единственное решение исходного уравнения x = 0.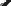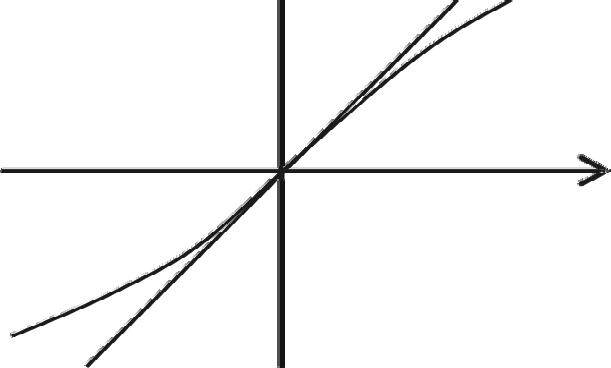






Приведенные примеры наглядно показывают возможности описанного метода. Метод вполне можно изучать со школьниками на факультативных и кружковых занятиях.

Уравнения для самостоятельного решения

1. 
   
   − −
   Решите уравнение x² + ln² x−ln x² −1 = 0.
   
2. 
   
   2
   Решите уравнение x² + log² x log₂ x⁴ 1 = 0.
   
3. 
   
   
   
   
   
   π
   Решите уравнение cos(x)+ sin(x) = 1.
   

4. 
   
   
   
   1+x²
   Решите уравнение ^√1+x
   

Ответы к уравнениям

1. 1.

2. 1; 2.


∈
3. 2πn, n Z. 4. 1.

= ^√2 ^{( 4} arctg x ³.

Литература

1. 
   Игнатов Ю.А. Всероссийские студенческие турниры математических боёв. Тула, 2002 – 2015. В 2-х ч. Часть I / Игнатов Ю.А., Шулюпов В.А., Реброва И.Ю. и др. - Тула: Изд-во ТГПУ им. Л.Н. Толстого, 2016. - 148 с.
   
2. 
   Игнатов Ю.А. Комбинация метода подстановки с графическим методом при решении уравне- ний / В сб. Модернизация методического обеспечения и организационного сопровождения учебно- го процесса в контексте нового закона “Об образовании в Российской Федерации”: Материалы XL учебно-методической конференции ППС, аспирантов, магистрантов, соискателей ТГПУ им. Л.Н. Тол- стого. - Тула: Изд-во Тул. гос. пед. ун-та им. Л.Н. Толстого, 2013. - С. 75-78.
   

Игнатов Юрий Александрович, доцент кафедры алгебры, математического анализа и геометрии Тульского государственного педагогического университета

им. Л.Н. Толстого, кандидат физ.-мат. наук. E-mail: [e-mail]