11 класс.функции.егэ. График функции. Исследование функций и построение их графиков элементарными методами
 Скачать 216 Kb. Скачать 216 Kb.
|
|
Алгебра и начала анализа.11класс Тема: График функции. Исследование функций и построение их графиков элементарными методами. Форма урока: Урок обобщающего повторения материала. Цели и задачи урока: Обучающие: Обобщить и систематизировать понятие функции, основные свойства функций; сформировать умение применять эти свойства при решении упражнений базового и повышенного уровней сложности; сформировать умение строить графики любой функции с помощью преобразований и проводить их исследование по схеме. Отработать в интерактивном режиме элементарных базовых умений и тем самым повысить уровень возможностей учащихся в овладении умениями комплексного характера при закреплении темы «Функции». Воспитательные: Воспитывать ответственность за достигнутый результат, сознательное отношение к учебе и предмету, воспитать в учениках целеустремлённость в достижении положительного результата и прочного познавательного интереса к математике. Развивающие: Обеспечить развитие конструкторско-практической деятельности учащихся на уровне, соответствующем уровню уже сформированных у них знаний, направленной на формирование наглядно-образного мышления, внимания, воображения и творчества. Ожидаемый результат: Сформировать у учащихся прочные знания, умения и навыки по основным понятиям темы «Функции». Ход урока: I. Организационный момент: подготовка рабочего места учащегося, проектор с выводом изображения на экран II.Мотивация целей урока: На прошлом уроке мы с вами работали с понятием функция и ее свойства. Как показывает практика, одной из проблемных тем ЕГЭ является тема: «Свойства функций» Сегодня мы постараемся обобщить все знания по этой теме. В ЕГЭ встречаются задания на нахождение чётных-нечётных и периодических функций, область определения и область значения. Поэтому более подробно остановимся именно на этих моментах, но и повторим все остальные свойства. III. Математический диктант (с самопроверкой) Устная работа. Найти соответствия между формулами и графиками функций 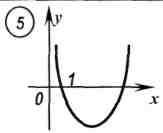 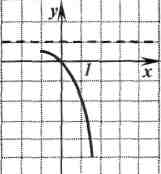  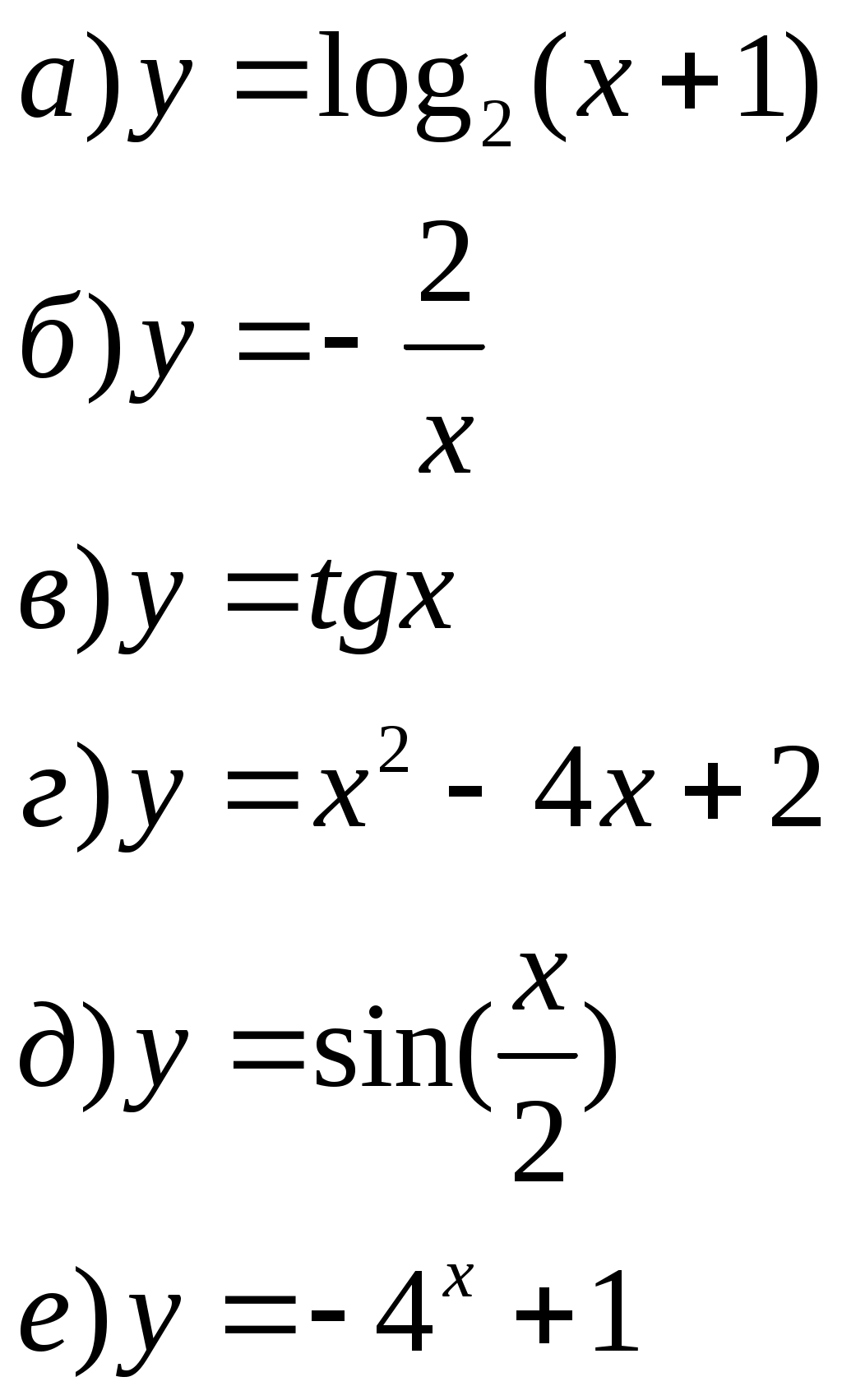 IV. Повторение теоретического материала: Что такое Функция? Определение 1. Зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у, называется функцией. Определение 2. Соответствие f между двумя множествами Х и У, при которой каждому элементу множества Х ставится в соответствие единственный элемент множества У, называется функцией у = f(х) Посмотрите на графики и найдите график(графики), не являющиеся графиками функции и почему? (Приложение 1. график № 10 ) Перечислите, какими свойствами может обладать функция? Общая схема исследования функции: Область определения функции Область значений функции Определение точек пересечения графика функции с осями координат Исследование функции на чётность Исследование функции на периодичность Определение промежутков знакопостоянства Исследование функции на монотонность Исследование функции на экстремум Исследование поведения функции на границах области определения Комментарий учителя: Теперь, двигаясь по пунктам схемы, будем вспоминать необходимые определения, и демонстрировать соответствующие свойства функции на графиках. I пункт: Область определения функции Определение: Область определения функции – это множество значений независимой переменной, при которых функция имеет смысл. Перед вами графики функций. Для каждого графика назовите область определения соответствующей функции. (слайды) II пункт: Область значений функции Определение: Областью значения функции называется множество, в которое входят все значения, которые может принимать функция на своей области определения. Перед вами графики функций. Для каждого графика назовите область значения соответствующей функции. (слайды) Комментарий учителя: По графикам функций найти область определения и область значения достаточно просто . Давайте попробуем найти их аналитически. Найдите область определения функций: (Решаем вместе, у доски ученики проговаривают ) а) Ответы а) Найдите область значения функций: (Решаем вместе, у доски ученики проговаривают ) а) Ответы а) III пункт: Определение точек пересечения графика функции с осями координат Определение: а) если х=0 € D(f), то по определению функции точка пересечения с осью Оу единственная и имеет координаты (0; f(0)) б) если f(х)=0, то число решений равно количеству точек пересечения графика функции с осью Ох. Комментарий учителя: Заметим, что в некоторых случаях ось абсцисс является касательной к графику функции. В этих случаях их общую точку будем считать точкой пересечения (12 пример). График функции может совпасть с осью Ох (3 пример). В этом случае график и ось имеют бесконечно много общих точек. IVпункт: Исследование функции на чётность Определение: Если область определения функции симметрична относительно оси Оу и для любого х из области определения выполняется равенство f (-x)= f(x), то функция чётная, а если область определения функции симметрична относительно нуля и для любого х из области определения выполняется равенство f(-x) = -f (x), то функция нечётная, если не выполняется ни одно из равенств, то функция ни чётная, ни нечётная. Комментарий учителя: Обратите внимание на функцию № 3 она и чётная и нечётная Vпункт: Исследование функции на периодичность Комментарий учителя: Свойством периодичности обладают не все функции. Определите графики периодических функций и укажите их период (слайды) Определение: Если существует такое число t #0, что для любого х из области определения функции у = f(х) числа х+t и х- t принадлежат области определения и f(х+t)=f(х-t)=f(х), то функция называется периодической, а число t – периодом функции. Комментарий учителя: Принято определять, если это возможно, наименьший положительный период T. VI пункт: Определение промежутков знакопостоянства Определение: Множество Х, на котором функция не меняет свой знак, называется промежутком знакопостоянства функции. Определите промежутки знакопостоянства данных функций (слайды) VII и VIII пункт: Исследование функции на монотонность и на экстремум Эти два пункта исследования функции тесно связаны между собой. Рассмотрим их вместе. Определение1: Если для любых х1 и х2 € Х и таких, что х1>х2, выполнено условие f(х1)>f(х2), то функция у=f(х) называется монотонно возрастающей на Х. Если f(х1) Определение2: Если в некоторой точке х0 значение функции не меньше значений функции вблизи этой точки, то точка х0 называется точкой максимума, а f(х0) – максимум функции. Если в некоторой точке х0 значение функции не больше значений функции вблизи этой точки, то точка х0 называется точкой минимума, а f(х0) – минимум функции. Максимум функции и минимум функции называются экстремумами функции, а точки минимума и максимума – точками экстремумов. Комментарий учителя: Определение промежутков монотонности и экстремумов функции можно провести с помощью графика производной данной функции. Определите промежутки монотонности и экстремумы данных функций (слайды) Таким образом, мы с вами вспомнили все свойства, которыми может обладать функция. Чтобы убедиться в продуктивности потраченного времени проведём не большую самостоятельную работу VI.Самостоятельная работа (обучающегося характера по материалам ЕГЭ): На рисунке изображён график функции y = f(x) . Точки a, b, c, d и e задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной. 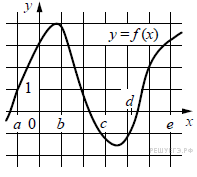
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1]. ГРАФИКИ 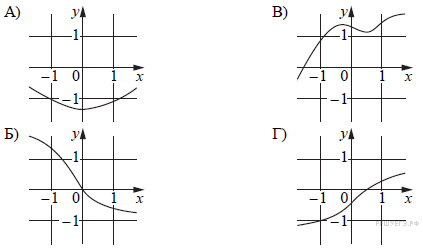 ХАРАКТЕРИСТИКИ 1) Функция принимает отрицательное значение в каждой точке отрезка [−1; 1]. 2) Функция возрастает на отрезке [−1; 1]. 3) Функция принимает положительное значение в каждой точке отрезка [−1; 1]. 4) Функция убывает на отрезке [−1; 1]. Найдите наименьшее значение функции Найдите точку минимума функции VII. Рефлексия: И так давайте подведём итоги: что нового вы сегодня узнали, чему научились? (Следуют ответы учащихся) VIII. Домашнее задание: п. 1.5 прочитать, выучить правила. Построить график функции и исследовать ее по алгоритму (см. п. 1.5) №1.55(б,г) Памятка Что такое Функция? Определение 1. Зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у, называется функцией. Определение 2. Соответствие f между двумя множествами Х и У, при которой каждому элементу множества Х ставится в соответствие единственный элемент множества У, называется функцией у = f(х) Iпункт: Область определения функции Определение: Область определения функции – это множество значений независимой переменной, при которых функция имеет смысл. IIпункт: Область значений функции Определение: Областью значения функции называется множество, в которое входят все значения, которые может принимать функция на своей области определения. IIIпункт: Определение точек пересечения графика функции с осями координат Определение: а) если х=0 € D(f), то по определению функции точка пересечения с осью Оу единственная и имеет координаты (0; f(0)) б) если f(х)=0, то число решений равно количеству точек пересечения графика функции с осью Ох. IVпункт: Исследование функции на чётность Определение: Если область определения функции симметрична относительно оси Оу и для любого х из области определения выполняется равенство f (-x)= f(x), то функция чётная, а если область определения функции симметрична относительно нуля и для любого х из области определения выполняется равенство f(-x) = -f (x), то функция нечётная, если не выполняется ни одно из равенств, то функция ни чётная, ни нечётная. VI пункт: Определение промежутков знакопостоянства Определение: Множество Х, на котором функция не меняет свой знак, называется промежутком знакопостоянства функции. VII и VIII пункт: Исследование функции на монотонность и на экстремум Определение1: Если для любых х1 и х2 € Х и таких, что х1>х2, выполнено условие f(х1)>f(х2), то функция у=f(х) называется монотонно возрастающей на Х. Если f(х1) Определение2: Если в некоторой точке х0 значение функции не меньше значений функции вблизи этой точки, то точка х0 называется точкой максимума, а f(х0) – максимум функции. Если в некоторой точке х0 значение функции не больше значений функции вблизи этой точки, то точка х0 называется точкой минимума, а f(х0) – минимум функции. Максимум функции и минимум функции называются экстремумами функции, а точки минимума и максимума – точками экстремумов. Приложение 1 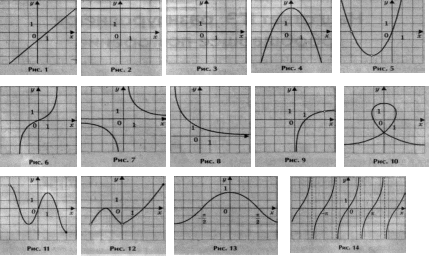 |
