Биоразнообразие 1 ч.. I. Биологическое разнообразие и методы его оценки Введение

• Название: I. Биологическое разнообразие и методы его оценки Введение
• Анкор: Биоразнообразие 1 ч..doc
• Дата: 05.03.2018
• Размер: 1.52 Mb.
• Имя файла: Биоразнообразие 1 ч..doc
• Тип: Анализ; #16277
• страница: 18 из 24

5.4. Индексы биоразнообразия

В настоящее время предложено более 40 индексов, которые предназначены для оценки биоразнообразия. Индексы, применяемые в анализе разнообразия сообществ, должны удовлетворять следующим требованиям [Песенко, 1982]:

1) разнообразие сообщества тем выше, чем больше в нем количество видов;

2) разнообразие сообщества тем выше, чем выше его выравненность.

Большинство различий между индексами, измеряющими биоразнообразие, заключается в том, какое значение они придают выравненности и видовому богатству.

5.4.1. Индексы видового богатства

Важной мерой оценки разнообразия для ограниченного в пространстве и во времени сообщества, для которого точно известно число составляющих его видов и особей, является видовое богатство. Однако в большиинстве случаев исследователь имеет дело с выборкой, не располагая полным списком видов сообщества. В этом случае необходимо использовать «нумерическое видовое богатство», т. е. число видов на строго оговоренное число особей или на определенную биомассу, и видовую плотность.

Видовая плотность (например, на 1 м²) – наиболее распространенный показатель видового богатства, особенно среди ботаников и почвенных зоологов.Показатель «нумерическое видовое богатство» используется реже, хотя более популярно его применение при исследовании водных объектов. Например, при исследовании экологических воздействий на сообщества рыб можно использовать показатель число видов на 1000 рыб.

Не всегда можно добиться равного размера всех выборок. Но следует всегда помнить, что при увеличении объема выборки число видов всегда растет.

Различные сочетания S (число выявленных видов) и N (общее число особей всех S видов) лежат в основе простых показателей видового разнообразия:

индекса видового богатства Маргалефа:

;

индекса видового богатства Менхиника:

.

Например, 5 октября 1997 года в Театральном парке г. Ростова-на-Дону в результате экскурсии была получена выборка, которая насчитывала 17 видов птиц, представленных 149 особями. Разнообразие будет составлять: по индексу Маргалефа – D_Mg = 3,2 , по индексу Менхиника – D_Mn = 1,4.

Достоинство этих индексов – легкость расчетов. Большая величина индекса соответствует большему разнообразию.

Для оценки видового богатства Кемптоном и Тейлором в 1976 году был предложен индекс Q, учитывающий распределение видовых обилий, но не требующий соответствия какой-либо модели.

Этот индекс представляет собой меру межквартильного наклона кривой накопленного видового обилия и обеспечивает измерение разнообразия сообщества, не отдавая предпочтения ни очень обильным, ни очень редким видам. Несколько ранее индекс, основанный на сходной идее, был предложен Уиттекером, однако он учитывал всю кривую видовых обилий и давал ошибки на обоих концах распределения.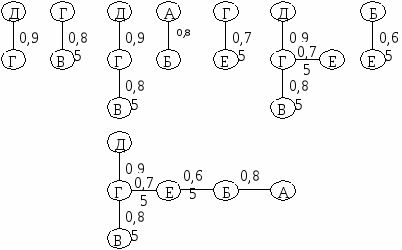



Рис. 5.4.1. Графическая интерпретация индекса Q
Индекс Q рассчитывается по эмпирическим данным.

,

где n_r – общее число видов с обилием R;  – общее число видов в выборке; R1, R2 – нижний и верхний квартили; n_R1– число особей в классе, соответствующем R1; n_R2– число особей в классе, соответствующем R2 (рис. 5.4.1).

По оси абсцисс откладывается обилие видов в логарифмическом масштабе (log₁₀), а по оси ординат – накопленное число видов. Индекс Q – наклон Q между двумя квартилями. Если выборки малы, индекс Q может смещаться. Однако эта ошибка невелика, если в выборку попадает более 50% всех видов. Некоторые ученые находят, что Q =  логарифмического распределения. Для лог-нормальной модели Q = 0,371 S/.

5.4.2. Индексы, основанные на относительном обилии видов

Эту группу индексов называют индексами неоднородности, так как они учитывают одновременно и выравненность, и видовое богатство. Индексы, основанные на относительном обилии видов, относятся к непараметрическим, поскольку они не требуют никаких предположений о распределениях. Их применение углубляет оценки биоразнообразия по сравнению с индексами видового богатства, которые опираются лишь на один параметр.

Выделяются две категории непараметрических индексов:

1) индексы, полученные на основе теории информации (информационно-статистические);

2) индексы доминирования.

Индекс Шеннона – Уивера. Макартур [1955] и Маргалеф [1957] впервые применили для оценки к исследованию видовой устойчивости и разнообразия сообщества теорию информации. Теория информации основывается на изучении вероятности наступления цепи событий. Результат выражается в единицах неопределенности, или информации. Шеннон в 1949 году вывел функцию, которая стала называться индексом разнообразия Шеннона. Расчеты индекса разнообразия Шеннона предполагают, что особи попадают в выборку случайно из «неопределенно большой» (т. е. практически бесконечной совокупности) генеральной совокупности, причем в выборке представлены все виды генеральной совокупности. Неопределенность будет максимальной, когда все события (N) будут иметь одинаковую вероятность наступления (p_i= n_i/N). Она уменьшается по мере того, как частота некоторых событий возрастает по сравнению с другими, вплоть до достижения минимального значения (нуля), когда остается одно событие и есть уверенность в его наступлении.

Индекс Шеннона рассчитывается по формуле:

H’= - p_i ln p_i,,

где величина p_i – доля особей i-го вида.

В выборке истинное значение p_i неизвестно, но оценивается как n_i/N.

Причины ошибок в оценке разнообразия с использованием этого индекса заключаются в том, что невозможно включить в выборку все виды реального сообщества.

При расчете индекса Шеннона часто используется двоичный логарифм, но приемлемо также использовать и другие основания логарифма (десятичный, натуральный)

Индекс Шеннона обычно варьирует в пределах от 1,5 до 3,5, очень редко превышая 4,5.

Дисперсию индекса Шеннона (VarH’) рассчитывают по формуле: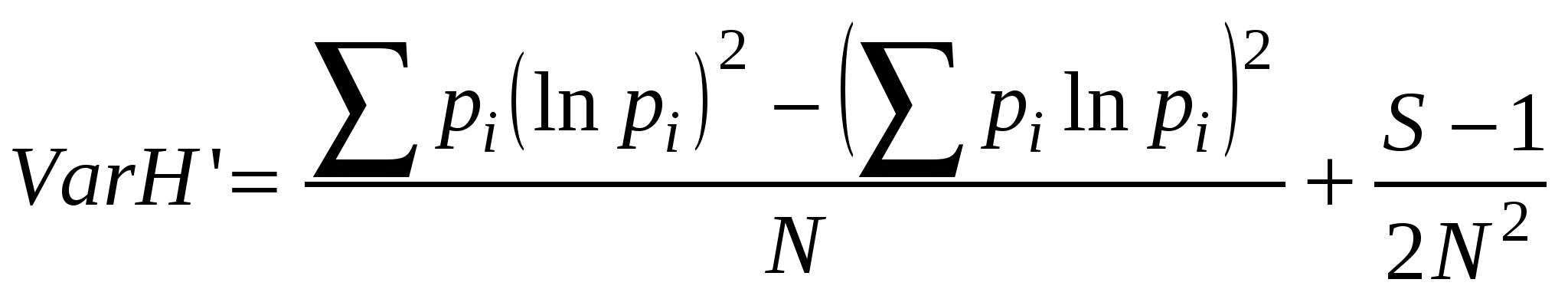

.

Если значения индекса Шеннона рассчитать для нескольких выборок, то полученное распределение величин подчиняется нормальному закону. Это свойство дает возможность применять мощную параметрическую статистику, включая дисперсионный анализ. Применение сравнительных параметрического и дисперсионного анализа полезно при оценке разнообразия различных местообитаний, когда есть повторности.

Для проверки значимости различий между выборочными совокупностями значений индекса Шеннона Хатчесон предложил использовать параметрический критерий Стьюдента: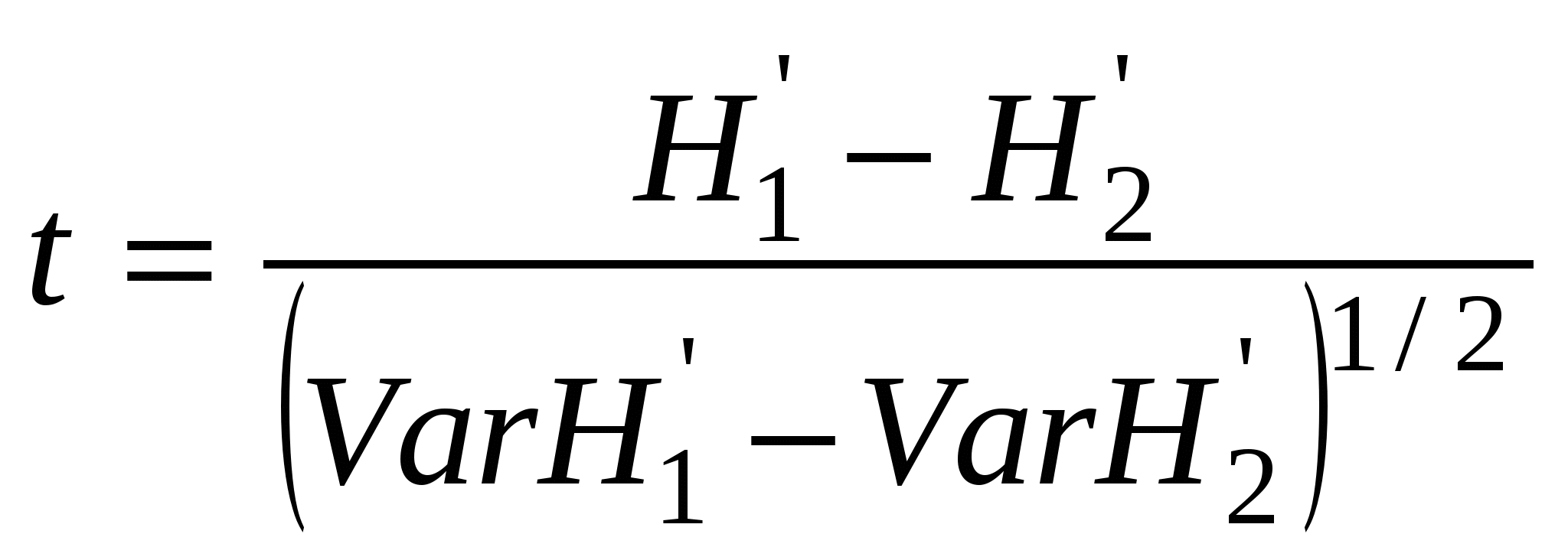

.

Число степеней свободы определяется по уравнению: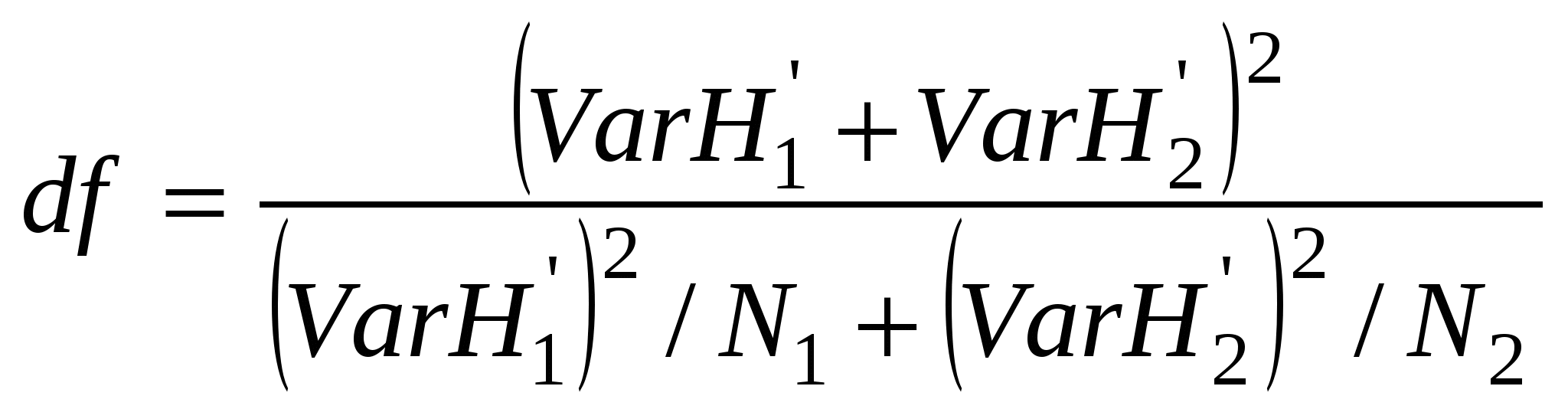

,

где N₁ и N₂ – общее число видов в двух выборках.

На основе индекса Шеннона можно вычислить показатель выравненности Е (отношение наблюдаемого разнообразия к максимальному):



E [0,1], причем E= 1 при равном обилии всех видов.

Индекс Шеннона оказался самым популярным в оценке данных по разнообразию и применяется чаще других.

Индекс Бриллуэна. Не всегда исследователи способны гарантировать случайный отбор объектов в выборочную совокупность или учесть все виды сообщества. Это происходит обычно из-за несовершенных методов отлова животных. Нельзя обеспечить случайность попадания объектов в выборку при отлове насекомых на свет (привлекаются виды, активные только ночью, и выпадают из списка видов формы с дневной активностью). Очень разнятся списки видов паукообразных, приносимых в гнезда большой синицей и собранных в биотопе традиционными методами, рекомендуемыми при сборе беспозвоночных. Подходящей формой информационно-статистического индекса в таких случаях может быть индекс Бриллуэна, определяемый по формуле:

.

Индекс Бриллуэна дает сходную с индексом Шеннона величину разнообразия, редко превышая 4,5. Однако при оценке одного и того же массива данных его величина ниже индекса Шеннона. Это объясняется тем, что в нем нет неопределенности, свойственной индексу Шеннона.

Выравненность определяется по формуле:

,

,

где [N/S] – целая часть отношения N/S, а r=N–S^.[N/S].

Этим индексом мало пользуются, так как он трудно вычисляется, и, если выборка мала, – приводит к неверным выводам. Однако этот индекс рекомендуется использовать, если оценивается коллекция, а не случайная выборка, и если известен полный состав сообщества.

Меры доминирования уделяют основное внимание обилию самых обычных видов, а не видовому богатству. Лучшим среди индексов доминирования считается индекс Симпсона. Его иногда называют «индекс Юла», поскольку он напоминает меру, разработанную Юлом для оценки словарного запаса.

Индекс Симпсона описывает вероятность принадлежности любых двух особей, случайно отобранных из неопределенно большого сообщества, к разным видам формулой:

D = p_i², где p_i – доля особей i-го вида.

Для расчета индекса используется формула, соответствующая конечному сообществу: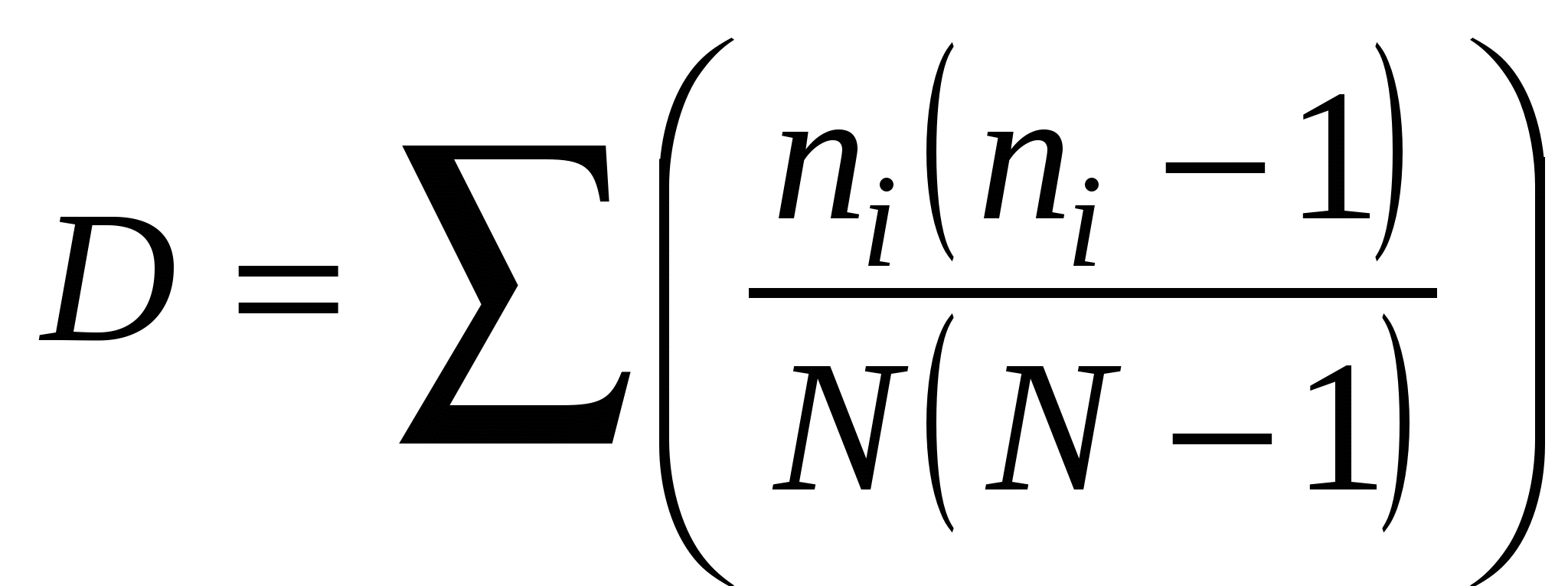

,

где n_i – число особей i-го вида, а N – общее число особей.

По мере увеличения D разнообразие уменьшается. Поэтому индекс Симпсона часто используют в форме (1– D). Эта величина носит название «вероятность межвидовых встреч» и варьирует от 0 до 1. Он очень чувствителен к присутствию в выборке наиболее обильных видов, но слабо зависит от видового богатства. Высокая или низкая величина индекса определяется типом распределения видовых обилий для случаев, когда число видов превышает 10. Многие авторы считают, что наилучшая мера – это «индекс полидоминантности»:

S_= 1/ D,

S_= ,

где i = 1,2,3,.... S ; S_[1; ].

Мера разнообразия Макинтоша. В 1967 году. Макинтош предложил рассматривать сообщество как точку в S-мерном гиперпространстве с координатами (n₁, n_2, ..., n_s). Тогда евклидово расстояние такого сообщества от начала координат можно использовать как меру его разнообразия:

.

Индекс Макинтоша U сам по себе не является индексом доминирования, однако, используя его, можно рассчитать меру разнообразия D, или доминирования, которая независима от объема выборки:

,

в дальнейшем можно рассчитать выравненность

.

Индекс Бергера – Паркера – одна из мер доминирования. Его достоинство – простота вычисления. Индекс Бергера-Паркера выражает относительную значимость наиболее обильного вида:

,

где N_max – число особей самого обильного вида.

Увеличение величины индекса Бергера – Паркера, как и индекса Симпсона, означает уменьшение разнообразия и увеличение степени доминирования одного вида. Поэтому обычно используется величина обратная индексу Бергера – Паркера 1/d.

Этот индекс независим от количества видов, но на него влияет объем выборки. Некоторые ученые считают этот индекс лучшей мерой разнообразия.