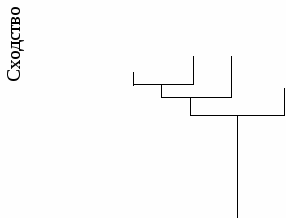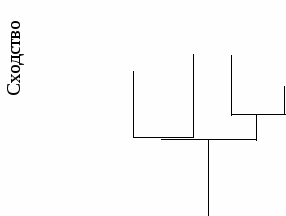Биоразнообразие 1 ч.. I. Биологическое разнообразие и методы его оценки Введение

• Название: I. Биологическое разнообразие и методы его оценки Введение
• Анкор: Биоразнообразие 1 ч..doc
• Дата: 05.03.2018
• Размер: 1.52 Mb.
• Имя файла: Биоразнообразие 1 ч..doc
• Тип: Анализ; #16277
• страница: 21 из 24

5.8. Графический анализ бета-разнообразия

Группирование и классификация выборок является следующим этапом в анализе бета-разнообразия. Эти процедуры выполняются на основе преобразования матриц, каждый элемент которой – это показатель сходства между двумя выборками.

5.8.1. Неориентированные и ориентированные графы

Для эффективного выделения скоплений объектов существу­ют методы сетевого анализа. Сетевой анализ матрицы оценок сходства между объектами заключается в построении некоторых типов графов, т.е. диаграмм, где объекты изображены в виде то­чек (кружков) – вершин графа, которые соединяются или не со­единяются линиями, называемыми ребрами графа. Степень соот­ветствия между объектами отражается в графах или характером взаимного расположения точек, или длиной и другими особенно­стями линии, соединяющих точки.

При анализе матриц сходства обычно используются «неориен­тированные графы», в которых линии, соединяющие вершины графа, не имеют направления. Реже применяются «ориентированные графы», в которых вершины соединены стрелками.

Дендрит – один из типов неориентированного графа. Он может быть двух типов: минимальное древо (матрица включает оценки различий между объектами) или максимальное древо (использу­ются меры сходства).

Дендрит – это ломаная линия, которая может ветвиться, но не содержит циклов. Построение дендрита заключается в нахож­дении для каждого объекта наиболее сходного с ним объекта и со­единении их линией. В результате получается ряд отрезков, в том числе и разветвленных.

Построить дендрит (рис. 5.8.1) можно с помощью матрицы сход­ства выборочных совокупностей, например (A–Е), вычисленной на основе индекса сходства Жаккара (табл. 5.8.1). Для этого после­довательно соединяем две наиболее сходные выборки Г и Д (0,90) отрезком. Следующая по силе величина сходства 0,85 обнаружена между выборками Г и В. Поэтому выборку В можно присое­динить отрезком к уже построенной ветке Д – Г и т. д.

Таблица 5.8.1

Матрица сходства выборочных совокупностей

	А	Б	В	Г	Д	Е
А	–	0,80	0,20	0,40	0,50	0,60
Б	0,80	–	0,30	0,55	0,45	0,65
В	0,20	0,30	–	0,85	0,15	0,10
Г	0,40	0,55	0,85	–	0,90	0,75
Д	0,50	0,45	0,15	0,90	–	0,25
Е	0,60	0,65	0,10	0,75	0,25	–

Основной недостаток этого графика – потеря информации, заключенной в матрице оценок сходства, в результате использования только немногих (максимальных для каждого объекта) значений показателя соответствия.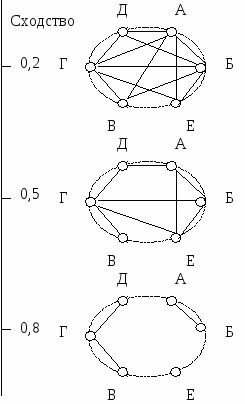



Рис. 5.8.1. Последовательные этапы построения дендрита на ос­нове матрицы сходства выборок

5.8.2. Плеяды Терентьева

Одним из видов графического анализа сходства выборок может быть построение плеяд Терентьева. Этот тип графика, в отличие от дендрита, учитывает всю матрицу сходства.

Плеяды Терентьева (рис. 5.8.2) также можно построить с помощью матрицы фаунистического сходства, вычисленной на основе индекса сходства Жаккара (табл. 5.8.1).

Этот тип графика является неориентированным графом. На нем все объекты могут быть соединены линиями, отражающими связи и меру сходства объектов. Толщина или характер линий соответ­ствуют определенному интервалу значений индекса сходства.

	1,0		Д	Г	В	Е	А	Б
	0,8
	0,6
	0,4
	0,2
	0

Рис. 5.8.2. Один из типов неориентированного графа – плеяд Терентьева, построенный на основе матрицы сходства выборок, где величины индекса сходства: 1 – [0,7: 0.9]; 2 – [0,4; 0,7]; 3 – [0,2: 0,4]
Другой графический вариант плеяд Терентьева показывает вза­имосвязи между выборками на разных уровнях сходства: 0,8, 0,5 и 0,2 (рис. 5.8.3).

	1,0		Д	Г	В	Е	А	Б
	0,8
	0,6
	0,4
	0,2
	0

Рис. 5.8.3. Один из типов плеяд Терентьева. Взаимосвязи между объектами показаны на уровнях сходства 0,8. 0,5 и 0,2
На уровне сходства 0,8 есть взаимосвязь между объектами Г и В, Г и Д, а также А и Б. На уровне сходства 0,5 прибавляются взаи­мосвязи между объектами Д и А, Г и Е, Г и Б, А и Е, Б и Е и т. д.

5.8.3. Дендрограмма (кластерный анализ)

Если сравнивать несколько участков, хорошее представление о бета-разнообразии может дать кластерный анализ.

Кластерный анализ – один из методов многомерного анализа, сущность которого состоит в иерархической классификации объек­тов в разделении множества объектов на однородные группы. Гра­фически иерархическая классификация отображается в виде дендрограммы (дерева).

Внутри каждой группы, получаемой в результате разбиения объектов на кластеры (группы), объекты более сходны, чем с объек­тами из других групп. Кластерный анализ начинается с составле­ния матрицы сходства для каждой пары сравниваемых объектов. Затем проводится последовательное объединение объектов в груп­пы по степени их сходства, пока все они не будут включены в одну группу. Поскольку интерпретация результатов кластерного анали­за зависит от визуальной оценки дендрограммы, лучше всего ис­пользовать этот прием для малых массивов данных.

В качестве примера рассмотрим кластеризацию выборок на ос­нове матрицы индексов сходства (табл. 5.8.1). Простейшие методы кластерного анализа, применяемого в биоценологии, биогеографии и числовой таксономии разными авторами, описаны Ю. А. Песенко [1982]. Эти методы могут быть с успехом использованы и в эколо­гических исследованиях при анализе бета-разнообразия.

	1,0		Д	Г	В	Е	А	Б
	0,8
	0,6
	0,4
	0,2
	0

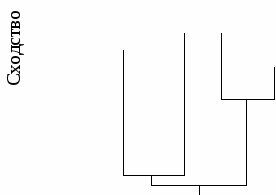
Рис. 5.8.4. Дендрограмма кластерного анализа шести объектов, построенная методом одиночного присоединения (ближайшего соседа)

В наиболее простых случаях процесс группировки начинается с нахождения в матрице индексов сходства пары наиболее сходных объектов. Самыми близкими объектами в примере, рассмотренном в табл. 5.8.1, являются Г и Д (0,90). Эти объекты отображаются на гра­фике двумя соседними точками (рис. 5.8.4).

Отходящие от точек параллельные линии соединяются отрез­ком на уровне величины сходства и объединяются в один кластер. Затем в матрице индексов сходства находится второй по величине индекс сходства. Если он связывает два других, еще не объединен­ных в группу объекта, то их соединяют так же, как и первые два, но отдельно от них на соответствующем уровне сходства. В нашем примере вторая по силе связь имеется между объектами Г и В (0,85), при этом один из этих объектов уже объединен в кластер. В этом случае присоединение связанного с ним нового объекта может быть произведено тремя разными способами: одиночным, полным и сред­ним присоединением.

Одиночное присоединение называют также «методом ближнего соседа». Метод впервые использован Серенсеном в 1948 году. Соеди­нение групп производится по максимальному значению сходства между объектами из каждой группы. Следуя этому методу, объект В присоединяется к объектам ДГ, уже объединенным в кластер. Следующее по величине сходство – между объектами А и Б (0,80). Они объединяются в отдельный кластер на уровне сходства. Следующий шаг – присоединение объекта Е к группе из объединен­ных ранее объектов ДГВ, так как между объектами Е и Г сходство равно 0,75. На последнем этапе объединяются два сформирован­ных ранее кластера ДГВЕ и АБ в один на уровне 0,60. Результаты объединения показаны на рис. 5.8.4.

Полное присоединение называется также «методом дальнего соседа». Метод был впервые предложен Снитом в 1957 году Соглас­но этому правилу, после формирования кластеров ДГ и АБ к груп­пе АБ присоединяется объект Е, так как минимальное сходство этого объекта с объектами этого кластера равно 0,60. Объект В присоединяется к группе ДГ только на уровне 0,15 (минимальное сходство с каждым из объектов группы). Этот объект нельзя при­соединить к кластеру ЕАБ, так как минимальное сходство объек­та Е с объектами этой группы всего 0,1. Результаты объединения показаны на рис. 5.8.5.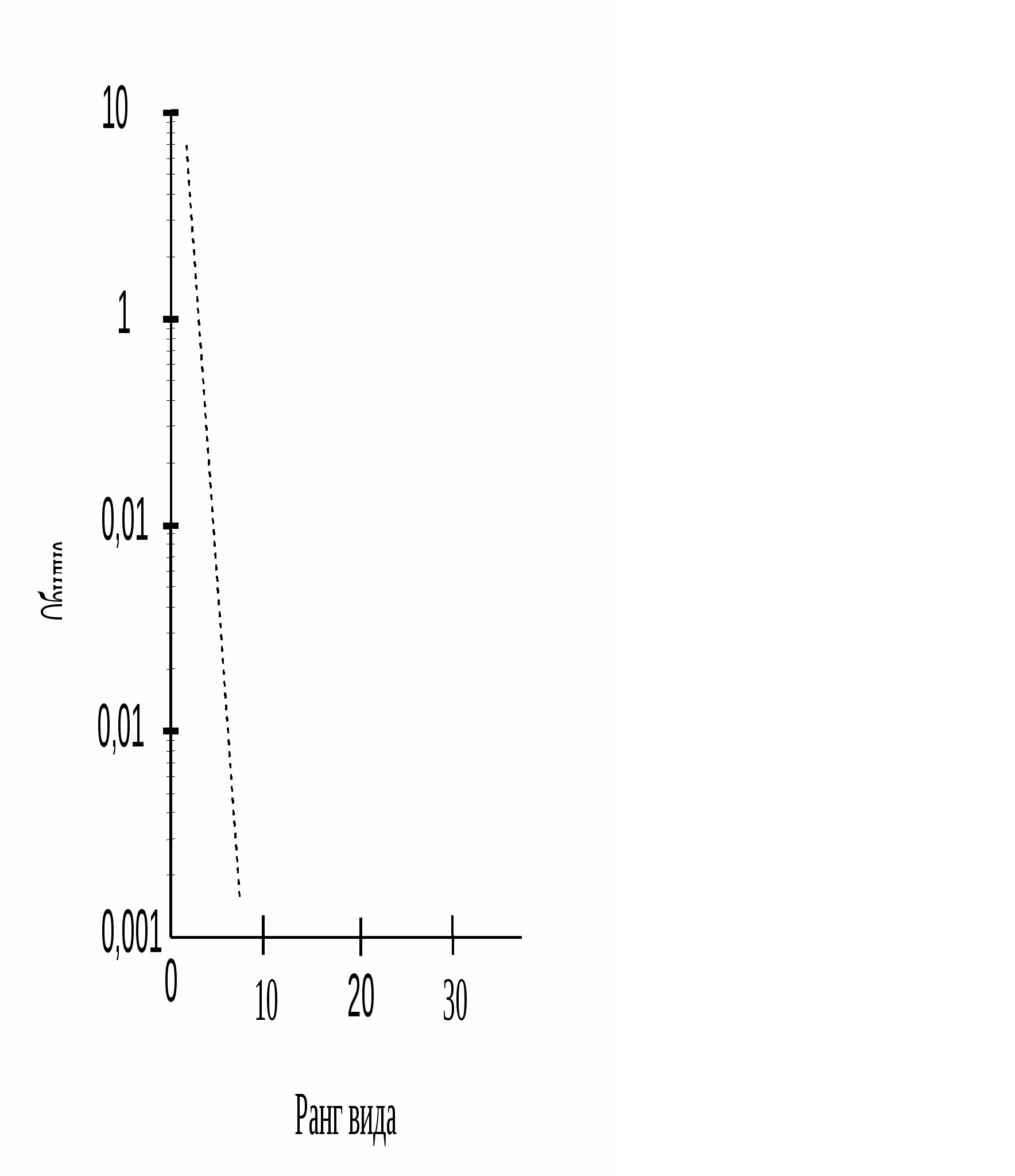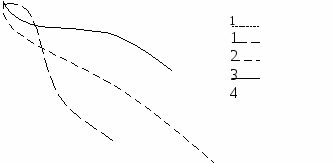



Рис. 5.8.5. Дендрограмма кластерного анализа шести объектов, построенная методом полного присоединения (дальнего соседа)
С
1
2

3

4


реднее присоединение.Этот метод включает несколько вари­антов. Он был предложен в 1958 году Сокалом, Майченером и Олсоном, Миллером одновременно. Один из самых простых вариан­тов этого вида кластерного анализа заключается в использовании средних арифметических невзвешенных значений сходства при­соединенного объекта со всеми объектами группы. Соединяются кластеры, среднее сходство между объектами которых выше. Со­гласно этому методу, после формирования кластеров ДГ и АБ к группе АБ присоединяется объект Е, так как среднее сходство этого объекта с объектами этого кластера (0,6 + 0,65)/2 = 0,625. Этот объект нельзя присоединить к кластеру В (сходство всего 0,10) или кластеру ДГ (среднее сходство равно 0,50). На следующем шаге к группе ДГ присоединяется объект В, так как среднее сход­ство его с объектами данного кластера равно 0,5, а с группой ЕАБ – лишь 0,20. Последний шаг – объединение двух групп ДГВ и ЕАБ в один кластер на уровне 0,49, так как эта величина пока­зывает среднюю связь между объектами в двух группах. Резуль­таты объединения показаны на рис. 5.8.6.



Рис. 5.8.6. Дендрограмма кластерного анализа шести объектов, построенная методом среднего присоединения
Более сложные и разнообразные методы кластерного анализа реализуются с помощью вычислительной техники. Разработано множество статистических пакетов программ, таких как Statgraphics, Statistica, STADIA и другие, которые выполняют кластерный анализ.