I и ii порядка Введение. Исследование
 Скачать 4.42 Mb. Скачать 4.42 Mb.
|
|
3. Дифференциальное уравнение первого порядка с разделяющимися переменными. Определение. Дифференциальное уравнение первого порядка  называется уравнением с разделяющимися переменными, если оно может быть представлено в виде 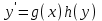 или или 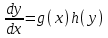 . .Разнося переменные x и y и их дифференциалы в разные стороны такого уравнения, оно может быть записано в виде 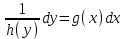 (отсюда происходит название данного типа уравнения). (отсюда происходит название данного типа уравнения).Можно следующую интерпретацию происхождения данного уравнения. Пусть величина Z является с одной стороны функцией величины y, т.е. z=M(y). С другой стороны величина Z является функцией величины x, т.е. z=g(x). Например, если Z-объем выпуска продукции, то с одной стороны z зависит от величины y – объема основных фондов, с другой стороны z может рассматриваться зависимой от величины x – объема затрачиваемых трудовых ресурсов. Таким образом, через соотношения z=H(y) и z=G(x) одна из величин y или x представляется функцией другой величины x или, соответственно, y. Исходное дифференциальное уравнение отображает эту функциональную связь через дифференциалы функций H(y) и G(x), уравнивая их, т.е. dz=dH(y)=dG(x). Отсюда можно считать, что 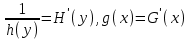 . .Таким образом, чтобы найти эту функциональную связь в виде y=y(x),x=x(y) или f(x,y)=0, надо проинтегрировать каждую из частей дифференциального уравнения, получая 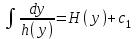 , , 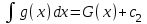 и затем приравнять их H(y)+c1=G(x)+c2 (имея в виду z=H(y)+c1, z=G(x)+c2, и затем z исключается). Вместо двух постоянных c1 и c2 обычно берется одна c=c2-c1, и тогда общее решение дифференциального уравнения записывается в виде и затем приравнять их H(y)+c1=G(x)+c2 (имея в виду z=H(y)+c1, z=G(x)+c2, и затем z исключается). Вместо двух постоянных c1 и c2 обычно берется одна c=c2-c1, и тогда общее решение дифференциального уравнения записывается в видеH(y)=G(x)+c. Если это возможно, из него одна из величин может быть представлена явно функцией другой y=y(x) или x=x(y). Пример 1. Рассмотрим дифференциальное уравнение получаемое при моделировании процесса распространения информации о новом товаре   . .Данное уравнение, очевидно, относится к уравнению с разделяющимися переменными. Разнеся переменные x и t и их дифференциалы по разные стороны, уравнение запишем в виде 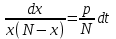 или или 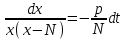 . .Проинтегрируем каждую из сторон этого уравнения: 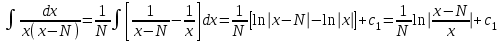 , , 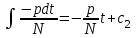 . .Приравнивая найденные интегралы получаем 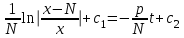 или или 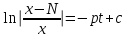 , ,где c=N(c1-c2). Отсюда далее 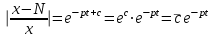 , где , где 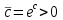 . Так как по смыслу задачи . Так как по смыслу задачи 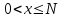 , то , то 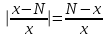 , и тогда , и тогда 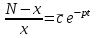 . Окончательно общее решение дифференциального уравнения получает вид . Окончательно общее решение дифференциального уравнения получает вид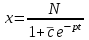 , где , где 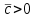 . .Нетрудно проверить, что дискретной и огибающей кривых дифференциальное уравнение не имеет. Однако беря крайние значения для 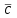 равные равные 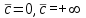 , получаем кривые x=N и x=0, являющиеся решениями уравнения, но не особыми. , получаем кривые x=N и x=0, являющиеся решениями уравнения, но не особыми.Пример 2. Возьмем дифференциальное уранение  или или 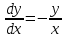 , ,геометрическая иллюстрация решений которого рассматривается в параграфе 2. Данное уравнение является с разделяющимися переменными> Разнося переменные в разные стороны, записываем уравнение в виде 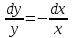 . .Интегрирование левой и правой частей уравнения, дает общее решение вида 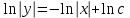 , где постоянная взята в виде lnc,c>0. Далее несложно преобразовать данное уравнение к виду , где постоянная взята в виде lnc,c>0. Далее несложно преобразовать данное уравнение к виду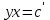 или или 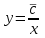 , где постоянная , где постоянная 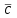 уже не имеет ограничений на знак. уже не имеет ограничений на знак.Как видно получилось семейство гипербол. Пусть из данного семейства интегральных кривых (гипербол) необходимо выделить кривую (решение) проходящую через точку M(1,1), т.е. выделить решение, удовлетворяющее начальному условию y(1)=1. Для этого в общее решение уравнения подставим значения x=1, y=1, и найдем, отвечающее искомой кривой, значение постоянной 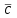 . Очевидно, это значение равно . Очевидно, это значение равно 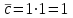 . Следовательно, искомое частное решение определяется уравнением . Следовательно, искомое частное решение определяется уравнениемYx=1 или 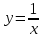 . .Пример 3. Рассмотрим уравнение  , приведенное в параграфе 3. Разрешая его относительно y/, получаем два уравнения y/=1 и y/=-1 или , приведенное в параграфе 3. Разрешая его относительно y/, получаем два уравнения y/=1 и y/=-1 или 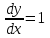 и и 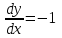 . .Оба являются с разделяющимися переменными и приводятся к виду dy=dx и dx=-dx. Интегрирование левых и правых частей уравнений дает следующие их общие решения y=x+c и y=-x+c. Пример 4. Следующим уравнением возьмем уарвнение 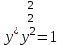 из примера в параграфе 4. из примера в параграфе 4.Разрешая его относительно y/ получаем 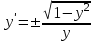 или или 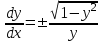 . .Разделяя переменные имеем 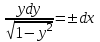 . .Найдем интегралы от левой и правой частей уравнения: 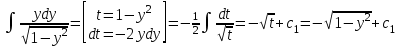 . .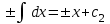 . .Приравнивая интегралы и заменяя две постоянных на одну получаем следующий вид общего решения уравнения 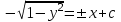 . .Возводя в квадрат обе части данного уравнения, получаем окончательный вид общего решения (x-c)2+y2=1. Пример 5. Решить дифференциальное уравнение 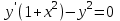 , ,Найти его частное решение при условии 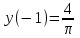 . .Разрешая уравнение относительно y/, видим, что оно является уравнением с разделяющимися переменными 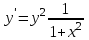 . .Разнося переменные по разные стороны уравнения получаем 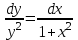 . .Интегрируя каждую из частей этого уравнения, получаем следующее общее решение исходного дифференциального уравнения 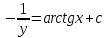 или или 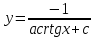 . .Используя начальное условие 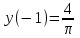 , определяем значение константы c для искомого частного решения , определяем значение константы c для искомого частного решения 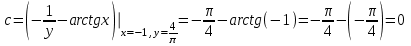 . Искомое частное решение дается уравнением . Искомое частное решение дается уравнением 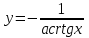 . .4. Однородное дифференциальное уравнение первого порядка. Функция f(x,y) называется однородной степени m, если 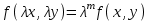 . .Функция f(x,y) называется однородной нулевой степени, если 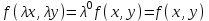 . .Например, функция 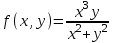 является однородной второй степени. Действительно, является однородной второй степени. Действительно, 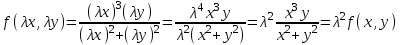 . Функция . Функция 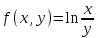 однородная нулевой степени, так как однородная нулевой степени, так как 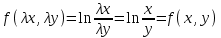 . .Всякая однородная функция нулевой степени может быть представлена в виде функции от отношения y/x (или отношения x/y). Действительно, пусть f(x,y) – однородная функция нулевой степени, тогда, взяв в качестве 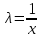 , имеем , имеем 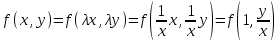 , где , где 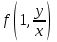 может рассматриваться как функция отношения y/x, т.е. может рассматриваться как функция отношения y/x, т.е. 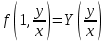 . .Определение. Дифференциальное уравнение первого порядка F(x,y,y/)=0, называется однородным, если оно может быть представлено в виде y/=f(x,y) или  ., где f(x,y) – однородная функция нулевой степени. ., где f(x,y) – однородная функция нулевой степени.Решение однородного дифференциального уравнения сводится к решению уравнения с разделяющимися переменными заменой y/x=u или y=ux, где u-функция от x. Подставляя в исходное уравнение 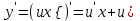 и и 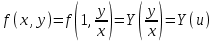 , получаем уравнение вида , получаем уравнение вида 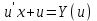 или или 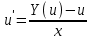 , являющиеся с разделяющимися переменными. Если u=g(x,c) или Ф(x,u,c)=0 является его общим решением, то y=xg(x,c) или Ф(x,y/x,c)=0 будет общим решением исходного уравнения. , являющиеся с разделяющимися переменными. Если u=g(x,c) или Ф(x,u,c)=0 является его общим решением, то y=xg(x,c) или Ф(x,y/x,c)=0 будет общим решением исходного уравнения.Пример 1. Рассматривается уравнение (x2-y2)dx+2xydy=0. Перепишем его в виде 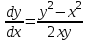 . Справа стоит функция однородная нулевой степени. Действительно, . Справа стоит функция однородная нулевой степени. Действительно, 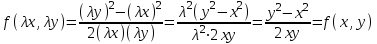 . Итак, преобразованное уравнение является однородным дифференциальным уравнением. Решаем его заменой y=ux. Получаем . Итак, преобразованное уравнение является однородным дифференциальным уравнением. Решаем его заменой y=ux. Получаем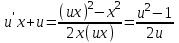 или или 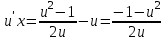 , т.е. , т.е. 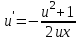 . .Разделяя переменные приходим к уравнению 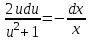 . .Интегрируем левую и правую части этого уравнения: 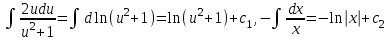 . .Приравнивая найденные интегралы, получаем общее решение вспомогательного дифференциального уравнения относительно переменных x и u 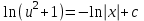 или или 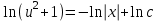 , где c>0. , где c>0.Потенциируя последнее выражение, общее решение получает вид 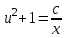 , где c – произвольная постоянная. , где c – произвольная постоянная.Заменяя u=y/x, получаем общий интеграл исходного дифференциального уравнения 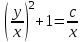 или y2+x2=cx, или y2+x2=cx,Последнее выражение приводится к виду 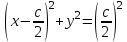 . .Таким образом, семейством интегральных кривых исходного уравнения является семейство окружностей с центрами в точках 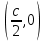 , лежащих на оси x, и радиусами , лежащих на оси x, и радиусами 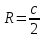 . Очевидно, все эти окружности касаются оси y в точке начала координат. На рис. 6 изображено семейство этих окружностей. . Очевидно, все эти окружности касаются оси y в точке начала координат. На рис. 6 изображено семейство этих окружностей.Пример 2. Требуется найти частное решение уравнения 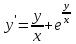 , ,Удовлетворяющих начальному условию y(1)=0. Нетрудно видеть (убедиться), что справа стоит однородная функция нулевой степени. Итак, исходное дифференциальное уравнение является однородным. Выполняя замену y=ux, приводим его к виду 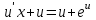 или или  . .Разделяем переменные, получаем 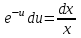 . .Интегрируя обе части этого уравнения, получаем общее решение вспомогательного дифференциального уравнения 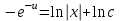 или или 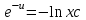 . .Подставим в него 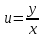 и получим и получим 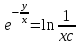 . Логарифмируя обе части этого уравнения получаем . Логарифмируя обе части этого уравнения получаем 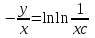 и далее и далее 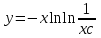 . .Последнее соотношение дает общее решение исходного дифференциального уравнения. Чтобы найти частное решение, воспользуемся начальными условиями x=1,y=0. Подставим их в общее решение 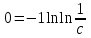 , отсюда , отсюда 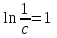 и и 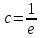 . .Таким образом, искомое частное решение имеет вид 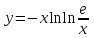 . .5. Линейное дифференциальное уравнение первого порядка. Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида y/+g(x)y=h(x). Такое название ему дано в связи с тем, что относительно переменных y и y/ его можно рассматривать как линейное. Если 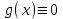 , то уравнение принимает простой вид y/=h(x), и сводится к нахождению неопределенного интеграла , то уравнение принимает простой вид y/=h(x), и сводится к нахождению неопределенного интеграла 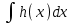 . Его общее решение тогда имеет вид . Его общее решение тогда имеет вид 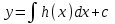 . .Если 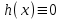 , то уравнение называется однородным линейным. Оно приобретает вид , то уравнение называется однородным линейным. Оно приобретает вид 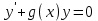 , и, как нетрудно видеть, сводится к решению уравнения с разделяющимися переменными , и, как нетрудно видеть, сводится к решению уравнения с разделяющимися переменными  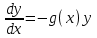 и далее и далее 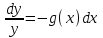 . .Его общее решение имеет вид 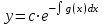 , где , где 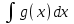 - некоторая первообразная для функции g(x). - некоторая первообразная для функции g(x).Предположим теперь, что 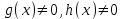 , функции g(x) и h(x) являются непрерывными. Пусть y=f(x,c) – искомое общее решение линейного дифференциального уравнения. , функции g(x) и h(x) являются непрерывными. Пусть y=f(x,c) – искомое общее решение линейного дифференциального уравнения.Представим исходное уравнение в виде 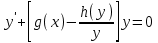 , ,и подставим в выражение, стоящее в квадратных скобках, 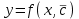 , т.е. как бы полагая в общем решении , т.е. как бы полагая в общем решении 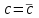 . Тогда вышеприведенное уравнение примет вид . Тогда вышеприведенное уравнение примет вид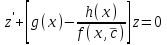 , ,являясь линейным однородным дифференциальным уравнением (в нем вместо y взята для удобства переменная z, чтобы не возникло путаницы решений этого уравнения с исходным). Общее решение этого уравнения, как уже отмечалось ранее, может быть представлено в виде 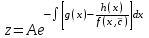 , ,где A – произвольная постоянная. Очевидно, 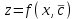 является его частным решением, и, следовательно, может быть получено при некотором значении является его частным решением, и, следовательно, может быть получено при некотором значении 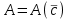 , т.е. , т.е.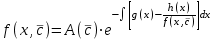 . .Если теперь освободиться от условия фиксирования постоянной 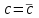 , то получаем, что общее решение исходного уравнения имеет вид , то получаем, что общее решение исходного уравнения имеет вид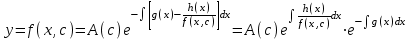 . .В нем второй множитель функция 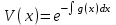 является, как нетрудно видеть, частным решением при c=1 однородного линейного уравнения является, как нетрудно видеть, частным решением при c=1 однородного линейного уравнения 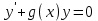 . Первый множитель функция . Первый множитель функция  представляет общее решение дифференциального уравнения u/v(x)=h(x). представляет общее решение дифференциального уравнения u/v(x)=h(x).Действительно, подставляя в это уравнение u/x(x,c), получаем тождество 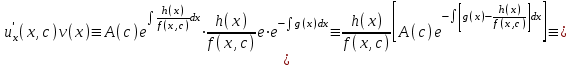 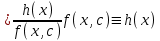 . .Таким образом, показано, что общее решение линейного дифференциального уравнения 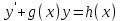 Представляется в виде y=u(x,c)v(x), где v(x) – частное решение однородного уравнения 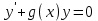 , решаемое при c=1, u(x,c) – общее решение уравнения u/v(x)=h(x). , решаемое при c=1, u(x,c) – общее решение уравнения u/v(x)=h(x).Нетрудно видеть, что в обоих случаях приходится решать уравнение с разделяющимися переменными. Заметим, что хотя при решении однородного уравнения 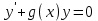 бралось частное решение V(x) однородного уравнения v/+g(x)v=0, бралось частное решение V(x) однородного уравнения v/+g(x)v=0,Являющегося уравнением с разделяющимися переменными. На втором этапе определяется решение u(x,c) дифференциального уравнения u/v(x)=h(x), Также являющегося уравнением с разделяющимися переменными. После их решений общее решение исходного линейного уравнения представляется в виде Y=u(x,c)v(x). Пример 1. Решить уравнение Y/+2y=sinx. Сначала решаем однородное уравнение v/+2v=0. Из него получаем 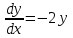 или или 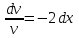 . .Интегрируя его левую и правую части, получаем его общий интеграл (решение) вида 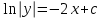 . .Полагая в нем c=0 и потенциируя его, получаем следующее его нетривиальное частное решение 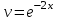 . .Далее решаем уравнение вида 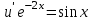 или или 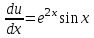 . .Разнося переменные в разные части уравнения и интегрируя их, получаем общее решение этого уравнения 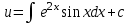 . .Вычислим интеграл: 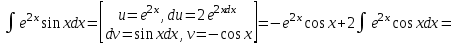 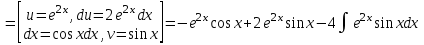 . .Рассматривая данное уравнение, как уравнение относительно интеграла, находим его вид 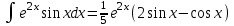 . .Следовательно, 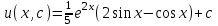 . .Тогда общее решение исходного уравнения будет 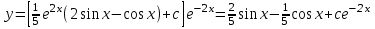 . .Предположим теперь, что требуется выделить частное решение, проходящее через точку M(0,0), т.е. решение, удовлетворяющее начальному условию y(0)=0. Для этого подставим значения x=0, y=0 в общее решение и найдем соответствующее значение постоянной c: 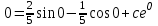 , отсюда , отсюда 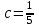 . .Искомым частным решением является 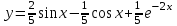 . .Пример 2. Решить уравнение 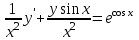 , ,являющееся линейным дифференциальным уравнением. На первом этапе найдем решение соответствующего линейного однородного уравнения 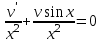 , или , или 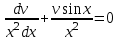 . .Разделяя переменные по разные стороны уравнения, имеем 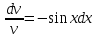 . .Интегрируя обе части данного уравнения, получаем следующее его частное решение 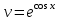 . .На втором этапе решаем уравнение вида 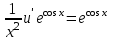 . .Делая замену 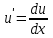 , сокращая обе части уравнения на , сокращая обе части уравнения на 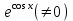 и разделяя переменные, имеем du=x2dx. и разделяя переменные, имеем du=x2dx.Интегрируя правую и левую части уравнения, получаем его общее решение 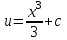 . .Общее решение исходного дифференциального уравнения имеет вид 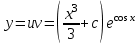 . . |
