Теплофикация и тепловые сети. И тепловые

• Название: И тепловые
• Анкор: Теплофикация и тепловые сети
• Дата: 27.03.2022
• Размер: 2.4 Mb.
• Имя файла: Теплофикация и тепловые сети.docx
• Тип: Учебник; #420164
• страница: 34 из 101

Рис. S.2. Кольцевая тепловая сеть от трех ТЭЦ

тания (рис. 5.2). В такую же систему могут быть в ряде случаев объединены тепловые сети ТЭЦ и крупных районных или про­мышленных котельных.

Объединение магистральных тепловых сетей нескольких источников теплоты на­ряду с резервированием теплоснабжения позволяет уменьшить суммарный котель­ный резерв на ТЭЦ и увеличить степень ис­пользования наиболее экономичного обо­рудования в системе за счет оптимального распределения нагрузки между источника­ми теплоты.

Блокирующие связи между магистраля­ми большого диаметра должны иметь дос­таточную пропускную способность, обес­печивающую передачу резервирующих по­токов воды. В необходимых случаях для увеличения пропускной способности бло­кирующих связей сооружаются насосные подстанции.

Независимо от блокирующих связей ме­жду магистралями целесообразно в городах с развитой нагрузкой горячего водоснабже­ния предусматривать перемычки сравни­тельно небольшого диаметра между смеж­ными распределительными тепловыми се­тями для резервирования нагрузки горячего водоснабжения.

При диаметрах магистралей, отходящих от источника теплоты, 700 мм и менее обычно применяют радиальную (лучевую) схему тепловой сети с постепенным умень­шением диаметра по мере удаления от стан­ции и снижения присоединенной тепловой нагрузки (рис. 5.3). Такая сеть наиболее де­шевая по начальным затратам, требует наи­меньшего расхода металла на сооружение и проста в эксплуатации. Однако при ава­рии на магистрали радиальной сети прекра­щается теплоснабжение абонентов, присое­диненных за местом аварии. Например, при аварии в точке а на радиальной магистрали 1 прекращается питание всех потребителей, расположенных по направлению трассы от ТЭЦ после точки а. Если происходит ава-



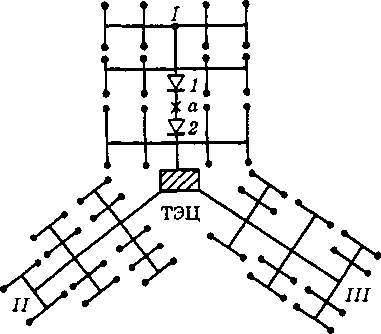
Рис. 5.3. Радиальная тепловая сеть

рия на магистрали вблизи станции, то пре­кращается теплоснабжение всех потребите­лей, присоединенных к магистрали. Такое решение допустимо, если время ремонта трубопроводов диаметром не менее 700 мм удовлетворяет вышесказанному условию.¹

2. 
   ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ
   

Уравнение Бернулли для установивше­гося движения по трубопроводу несжимае­мой жидкости, выражающее, отнесенный к единице массы, энергетический баланс этой жидкости без учета ее энтальпии, может быть записано в виде (рис. 5.4)



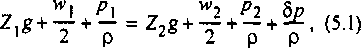
' Примечание научного редактора. Вопрос о том, при каких диаметрах теплопроводов какую схему тепловых сетей (радиальную или кольце­вую) следует применять в системах централизо­ванного теплоснабжения, должен решаться ис­ходя из конкретных условий, диктуемых надеж­ностью теплоснабжения потребителей теплоты допускают они перерыв в подаче теплоносителя или нет, каковы затраты на резервирование и т.п. Поэтому в условиях рыночной экономики указанная выше регламентация диаметров и схем тепловых сетей не может считаться един­ственно правильным решением.


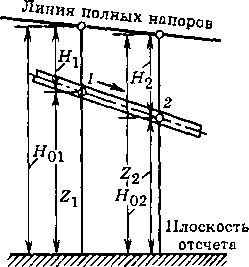
Рис. 5.4. Схема движения жидкости по трубо-
проводу

где Z, и Z₂ — геометрическая высота оси трубопровода в сечениях 1 и 2 по отноше­нию к горизонтальной плоскости отсчета, м; Wj и гг₂ — скорости движения жидкости в сечениях 7 и 2, м/с; p_t и р₂ — давления жидкости, измеренные на уровне оси трубо­провода в сечениях 7 и 2, Па; 8р — падение давления на участке 7—2; р — плотность жидкости, кг/м³; g — ускорение свободного падения, g = 9,81 м/с .

Первый член в (5.1)Zg— удельная энер­гия высоты в данном сечении, (отнесенная

к единице массы жидкости), Дж/кг; w /2 — удельная кинетическая энергия жидкости в данном сечении, Дж/кг; р/р — удельная потенциальная энергии жидкости в данном сечении, Дж/кг; 8р /р — удельная потеря потенциальной энергии жидкости из-за тре­ния и местных сопротивлений на участке трубопровода 7—2, Дж/кг, которая перехо­дит в теплоту, что приводит к увеличению удельной энтальпии жидкости в процессе ее движения по трубопроводу.

Наряду с удельной энергией в гидравли­ческом расчете тепловых сетей широко ис­пользуется другой параметр — напор, м,

Н_п = Z+^-+2 = Z + + 77, (5.2)

⁰ 2g у 2g

гдер—давление в трубопроводе, Па; р/у - Н— пьезометрический напор, м; у — удельный вес жидкости, Н/м³.

При гидравлическом расчете тепловых сетей, как правило, не учитывают отноше­ние w²/2g, представляющее собой скорост­ной напор потока в трубопроводе, так как он составляет сравнительно небольшую до­лю полного напора и изменяется по длине сети незначительно. Обычно принимают

Н^ = Z + р!"{-Z + Н, (5.3)

т.е. считают полный напор равным сумме пьезометрического напора и высоты распо­ложения оси трубопровода над плоскостью отсчета. Под пьезометрическим напором понимается давление в трубопроводе, вы­раженное в линейных единицах (обычно в метрах) столба той жидкости, которая пе­редается по трубопроводу.

Из (5.3) следует, что Н = 77_О - Z. Пьезо­метрический напор равен разности между полным напором и геометрической высо­той оси трубопровода над плоскостью от­счета. Падение давления и потеря напора в сети, или располагаемый перепад (раз­ность напоров), в сети связаны следующи­ми зависимостями:

877 = 8р/у = Sp/gp ; (5.4)

А = 7?/у = 7?/(gp), (5.5)

где 87/ — потеря напора или располагаемый напор, м; 8р — падение давления, или рас­полагаемый перепад давления, Па; A, R — удельная потеря напора (безразмерная ве­личина) и удельное падение давления, Па/м.

Падение давления в трубопроводе мо­жет быть представлено как сумма двух сла­гаемых: линейного падения и падения в ме­стных сопротивлениях

5р ^{= 8}Рл + ⁵Р_М> »⁶)

где 5р_;] — линейное падение давления; 8р_м — падение давления в местных сопро­тивлениях.

<— Рис. 5.5. Зависимость коэф-
фициента трения гладких труб
от числа Рейнольдса

Т Рис. 5.6. Разрез шероховатой
стенки трубы

Линейное падение 8р_л представляет со­бой падение давления на прямолинейных участках трубопровода. Падение давления в местных сопротивлениях 8р_м — это паде­ние давления в арматуре (вентилях, задвиж­ках, кранах и т.д.) и других элементах обо­рудования, размещенных неравномерно по длине трубопровода (коленях, шайбах, пе­реходах и т.п.).

Линейное падение давления. В трубо­проводах, транспортирующих жидкость или газы,

8р_л = /?_л/, (5.7)

где 8р_л — линейное падение давления на участке, Па; /?_л — удельное падение давле­ния, т.е. падение давления, отнесенное к единице длины трубопровода, Па/м; I — длина трубопровода, м.

Исходной зависимостью для определе­ния удельного линейного падения в трубо­проводе является уравнение Дарси

2 _г2 ? = 0.812Х-^-, (5.8)

^{2 d} ?р

где X — коэффициент гидравлического тре­ния (безразмерная величина); w— скорость

среды, м/с; р — плотность среды, кг/м³; d—внутренний диаметр трубопровода, м; G — массовый расход, кг/с.

Коэффициент гидравлического трения X зависит от состояния стенки трубы (гладкая или шероховатая) и режима движения жид­кости (ламинарное или турбулентное).

Поскольку гладкие трубы в техник транспортировки теплоты имеют ограни ченное применение (в основном в теплооб менных аппаратах), ниже приведены фор мулы для расчета коэффициента трени гладких труб без их подробного анализа:

Re < 2300 (ламинарное
движение), X = 64/Re,
2300< Re< 10⁴.

X = 0,3164/Re^0>25;
ReS 10⁴,

X = 1/(1,82 lgRe- 1,64)²;
Re > 10⁵,

X = 0,0032 + 0,221/Re^0,237.

На рис 5.5 показана зависимость коэф- фициента гидравлического трения гладки³¹ труб от числа Re.

Основное применение для транспорти­ровки теплоты имеют шероховатые сталь­ные трубы.

Шероховатую поверхность можно пред­ставить состоящей из ряда элементарных выступов к (рис. 5.6). В качестве первого характеристического параметра шерохова­тости принимают высоту выступа шерохо­ватости, называемую абсолютной шерохо­ватостью стенки. У большинства работаю­щих стальных трубопроводов она составля­ет в зависимости от технологии изготовле­ния труб и условий эксплуатации от 0,05

до 2 мм. В качестве второго характеристи­ческого параметра принимают отношение абсолютной шероховатости к радиусу тру­бопровода к/г, называемое относительной шероховатостью.

Как показывают исследования стальных труб, проведенные Г. А. Муриным в лабо­ратории теплофикации ВТИ, при малых числах Re коэффициент гидравлического трения X имеет максимальное значение. С увеличением числа Re коэффициент гид­равлического трения монотонно уменьша­ется и при некотором значении Re_np прак­тически достигает минимального значения. При дальнейшем увеличении числа Re ко­эффициент гидравлического трения остает­ся постоянным [66].

С достаточной для практических расче­тов точностью принимают, что в так на­зываемой переходной области, т.е. при 2300 < Re < Re_np, коэффициент гидравли­ческого трения зависит как от эквивалент­ной относительной шероховатости Х_э/г, так и от числа Re, а при Re > Re_np коэффи­циент гидравлического трения зависит только от к_э/г и не зависит от числа Re.

Под эквивалентной относительной ше­роховатостью реального трубопровода по­нимается искусственная относительная равномерная шероховатость цилиндриче­ской стенки, коэффициент гидравлического трения которой в области Re > Re_|]p такой же, как и в данном реальном трубопроводе.

Полученная опытным путем зависи­мость коэффициента гидравлического тре­ния стальных труб от числа Re и относи­тельной шероховатости хорошо описывает­ся универсальным уравнением, предложен­ным А.Д. Альтшулем [1],

X = 0,ll(X₃/rf+68/Re)°’²⁵. (5.9)

При &_э= 0 формула Альтшуля переходит в формулу Блазиуса. При Re = °° формула

Альтшуля переходит в формулу Б.Л. Шиф- ринсона [145]

X = 0,11(А_э/²⁵. (5.10)

Поскольку с увеличением числа Re зна­чение второго слагаемого в скобках в (5.9) резко уменьшается, то при больших числах Re расхождение между значениями X, най­денными по формулам Шифринсона и Альтшуля, получается незначительным.

Принимая допустимое расхождение в ко­эффициенте гидравлического трения по формулам Альтшуля и Шифринсона равным 3 %, из условия Хд/Хщ - 1 = 0,03 получаем

Re„_p = 568«//Х_э, (5.11)

где Х_А и Х,„ — значения X, рассчитанные по

9. 
   и (5.10). Поэтому при Re < 568<У/А_э ко­эффициент гидравлического трения должен определяться по (5.9), а при Re > Re_np > > 568сУ /А_э — по более простой формуле
   
10. 
    Б.Л. Шифринсона. Чем меньше отно­сительная шероховатость, тем больше зна­чение Re_np. При Re > Re_[ip практически имеет место квадратичная зависимость па­дения давления в трубопроводе от расхода.
    

На основе имеющихся материалов гид­равлических испытаний тепловых сетей и водопроводов в СНиП 2.04.07-86 рекомен­дуются следующие значения абсолютной эквивалентной шероховатости, м, для гид­равлического расчета тепловых сетей [130]:

Паропроводы 0,2*10 ³

Водяные сети в условиях

нормальной эксплуатации 0,5 ■ 10^-3

Конденсатопроводы и сети горячего водоснабжения 1 ■ КГ³

В тепловых сетях обычно Re > Re_np, по­этому тепловые сети, как правило, работа­ют в квадратичной области.

Формулу (5.8) для линейного падения давления в квадратичной области можно привести к виду, более удобному для прак­тических расчетов.

дены в табл. 5.1. В приложении 9 приведе­ны основные физические константы воды при температуре 0—200 °C.

Местное падение давления. При нали­чии на участке трубопровода ряда местных сопротивлений суммарное падение давле­ния во всех местных сопротивлениях, Па, определяется по формуле

² Г²

ьр_м = 20 ⁼ °’⁸¹²^—> <⁵-¹⁸)

рс?

где Ж — сумма коэффициентов местных сопротивлений, установленных на участке;

— безразмерная величина, зависящая от характера сопротивления.

Если представить прямолинейный тру­бопровод диаметром d, линейное падение давления на котором равно падению давле­ния в местных сопротивлениях, то длина та­кого участка трубопровода, называемая эк­вивалентной длиной местных сопротивле­ний, может быть найдена из равенства 190

5_Рм = /?_л/_э; (5.1

откуда эквивалентная длина местных с противлений, м,

/_э = (5.20

При подстановке в (5.20) коэффициен гидравлического трения по Шифринсш формула для эквивалентной длины мес ных сопротивлений приводится к виду

/_э = Я/2^¹’²⁵. (5.20<

Как видно из (5.206), эквивалентная дл1 на местных сопротивлений пропорционал: на сумме коэффициентов местных сопр< тивлений в первой степени и диаметру тр} бопровода в степени 1,25.

Коэффициенты местных сопротивлений а[ матуры и фасонных частей приведены в прилс жении 10

Коэффициент местного сопротивления зс движек и клапанов можно определить по фор муле [2]

• [(0.67' <⁵²¹

где п — степень сжатия сечения, т е отношени! сжатого сечения потока к площади поиеречногс сечения трубопровода:

При открытой задвижке	... п=1,	$ = о
При 50 %-ном открытии	... я = 0,5,	£ = 4,4
При 10 %-ном открытии	... я = 0,1,	£, = 235
При закрытой задвижке	... я = 0,	£ = ОО

Сопротивления муфтовых, фланцевых и сварных соединений трубопроводов при правильном выполнении незначительны, по­этому их надо рассматривать в совокупности с линейными сопротивлениями. Рекомендо­ванные выше значения абсолютной шерохо­ватости учитывают эти сопротивления.

Отношение падения давления в местных сопротивлениях трубопровода к линейному падению в этом трубопроводе представляет

где А_а = 5,1 /^’¹⁹ .

Для удобства уравнение (5.23) записыва­ется в следующем приближенном виде:




В пределах изменения а от 0 до 1 с по­грешностью ± 6 % можно принять

При транспортировке жидкости, в част­ности воды,

= Я_л/(1 + а) = /?.,(/ + /_э), (5.25)

откуда

Я_л = 5р/[/(1 +«)]. (5.26)

В табл. 5.1 приведены коэффициенты А, входящие в (5.12)—(5.24).

4. 
   ПОРЯДОК ГИДРАВЛИЧЕСКОГО РАСЧЕТА
   

При гидравлическом расчете трубопроводов обычно заданы расход теплоносителя и суммар­ное падение давления на участке. Требуется определить диаметр трубопровода. Расчет со­стоит из двух этапов: предварительного и прове­рочного.

Гидравлический расчет упрощается при ис­пользовании номограмм (рис. 5.7—5.9).

Предварительный расчет.

1. 
   Задаются долей местных потерь или вы­числяют ее по формуле (5.24).
   
2. 
   Находят удельное линейное падение дав­ления по (5.26).
   
3. 
   Определяют среднюю плотность теплоно­сителя на участке по формуле
   

Рср

(Рнач ⁺ Pko>J/2. (5.27)

Индексы «нач» и «кон» относятся к началу и концу участка. Если теплоноситель — жидкость, то принимают р_нач = р_кон = р_ср.

4. 
   Определяют диаметр трубопровода и? предположения его работы в квадратичной об­ласти по (5.13) или (5.16).
   

Проверочный расчет.

1. 
   Предварительно рассчитанный диаметр округляют до ближайшего по стандарту. Табли­ца стандартных диаметров труб, применяемых при транспортировке воды и водяного пара, при­ведена в приложении 11.
   
2. 
   Определяют число Re, сравнивают его с предельным Re_np, рассчитанный по (5.11). Уста­навливают расчетную область, в которой работа­ет трубопровод.
   

Когда трубопровод работает в квадратичной области, линейное удельное падение давления определяют по (5.12) и (5.15), эквивалентную длину местных сопротивлений — по (5.20), сум­марное падение давления — по (5.25).

Если трубопровод работает в переходной об­ласти, то по (5.9) вычисляют коэффициент гид­равлического трения X, находят по (5.8) удель-