Теплофикация и тепловые сети. И тепловые
 Скачать 2.4 Mb. Скачать 2.4 Mb.
|
|
Рис. 6.19. Принципиальная схема двухтрубной водяной тепловой сети с двумя статическими зонами (а) н пьезометрический график этой сети (б) 1 — обратный затвор; 2 — насосы на ТЭЦ; 3 — регулятор давления «до себя»; 4 — подпиточный насос верхней зоны; 5 — регулятор подпитки верхней зоны Эта задача решается с помощью уста новленных на дроссельной подстанции ре гулятора давления «до себя» 3 на обратно! линии и обратного клапана или затвора 1 н; подающей линии тепловой сети. При гидростатическом режиме системь теплоснабжения, т.е. когда сетевой насос 1 выключен, утечка сетевой воды из верхнег зоны восполняется водой из нижней зонь с помощью подпиточного насоса 4 и регулятора подпитки 5, установленных на подстанции. При гидродинамическом режиме обратный клапан или затвор 1 открыт, а регулятор 3 поддерживает за счет дросселирования заданный напор Нв в конце обратной линии верхней зоны района. На рис. 6.20, а показана схема двухтрубной водяной тепловой сети с насосной подстанцией 3 на обратной линии. Задача подстанции заключается в снижении давления в обратной линии у абонентов группы II, расположенных на значительном расстоянии от ТЭЦ и присоединенных к концевым участкам тепловой сети. Без насосной подстанции в обратной линии устанавливается давление, превышающее допустимое для отопительных установок, присоединенных к тепловой сети по зависимой схеме. Когда насосы на подстанции выключены, вода проходит по обратной линии между точками 5 и б через обратный клапан или затвор 2, установленный на обратной линии, минуя насосы. При включении в работу насосов 3 на подстанции возникает разность давлений между точками 6 и 5, равная перепаду давлений, развиваемому насосами. Под действием этой разности давлений закрывается обратный клапан или затвор 2, установленный на обратной линии, и весь поток воды проходит от точки 5 через подстанцию к точке 6. На рис. 6.20, бив приведены пьезометрические графики этой сети для двух вариантов: наличия регуляторов расхода у абонентов и отсутствия таковых. 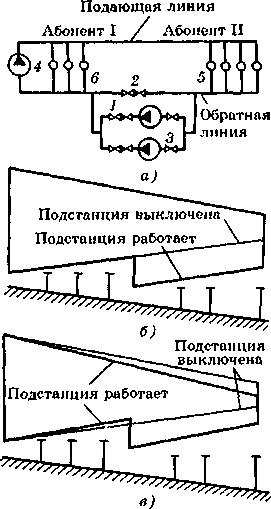 Рис. 6.20. Принципиальная схема двухтрубной водяной тепловой сети с насосной подстанцией на обратной линии и пьезометрический график этой сети а — принципиальная схема; б — пьезометрический график при автоматизированных вводах; в — то же при неавтоматизированных вводах; I — обратный затвор на насосной подстанции; 2 — обратный затвор на обратной линии; 3 — насосы на подстанции; 4 — насосы на ТЭЦ Если ГТП или абонентские вводы оснащены регуляторами расхода, поддерживающими постоянный расход сетевой воды через абонентские установки, то включение в работу насосной подстанции 3 не вызывает изменения расхода воды в тепловой сети. Полный напор во всех точках обратной магистрали перед насосной подстанцией уменьшается на значение полезного напора, развиваемого подстанцией. Если абонентские вводы не автоматизированы, то включение в работу насосной подстанции приводит к уменьшению суммарного сопротивления тепловой сети, поскольку насосная подстанция является отрицательным сопротивлением (6.22). Поэтому суммарный расход воды в тепловой сети возрастает. При этом в сети происходит разрегулировка. У абонентов, расположенных между ТЭЦ и насосной подстанцией, уменьшаются располагаемые напоры и расходы воды, а у абонентов, расположенных между насосной подстанцией и концевой точкой сети, располагаемые напоры и расходы воды возрастают. Задача расчета гидравлического режима такой тепловой сети заключается в опоеде- лении расходов воды в сети и располагаемых напоров в отдельных ее узлах после включения насосной подстанции. Известными являются сопротивления всех участков тепловой сети и абонентских систем, а также напоры насосов ТЭЦ и подстанции. Определение расходов воды проводится методом последовательных приближений, так как сопротивление насосной подстанции заранее неизвестно. Задаются предварительно расходом воды через насосную подстанцию, определяют сопротивление (отрицательное) насосной подстанции, подсчитывают суммарное сопротивление сети, определяют суммарный расход воды в тепловой сети и расход воды на отдельных ее участках, в том числе и через насосную подстанцию. Если предварительно выбранный расход воды через насосную не совпадает с полученным по расчету, то задаются другим, более близким к полученному расходом и расчет повторяют вновь до тех пор, пока предварительно выбранный расход воды через насосную подстанцию не совпадает с полученным по расчету. Значительно проще решается обратная задача, когда задан гидравлический режим сети при работе насосной подстанции и требуется рассчитать гидравлический режим сети при выключении подстанции. В этом случае сопротивление насосной подстанции известно, поскольку известен напор, развиваемый насосной подстанцией, и расход воды через нее. Задача сводится I\ p вой сети без насосной подстанции и к однозначному определению суммарного расхода в тепловой сети и расхода воды у отдельных абонентов по формулам (6.20) и (6.23). 6.7. РАСЧЕТ ПОТОКОРАСПРЕДЕЛЕНИЯ В КОЛЬЦЕВЫХ СЕТЯХ Тепловые сети современных крупных городов образуют многокольцевые системы. Расчет потокораспределения в таких системах — задача сложная, решаемая с помощью электронно-вычислительной техники или методами физического моделирования [39, 70, 136]. Принцип расчета потокораспределения в многокольцевых сетях основан на уравнениях Кирхгофа. В зависимости от оснащенности системы теплоснабжения авторегуляторами на практике встречаются два различных условия расчета (рис. 6.21). При наличии на групповых или местных подстанциях регуляторов расхода сетевой воды расчет заключается в определении расходов воды по отдельным участкам магистральной кольцевой сети по заданным сопротивлениям этих участков sK и заданным расходам воды Ку абонентов. При отсутствии на групповых или местных подстанциях регуляторов расхода расчет заключается в определении расхода сетевой воды в системе теплоснабжения и его распределения по участкам кольцевой сети по заданному перепаду давлений Др0 или располагаемому напору Но в узле 0 под- 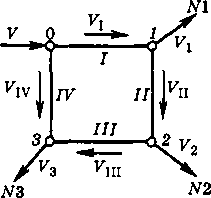 Рнс. 6.21. Схема однокольцевой сети распределению по участкам сети. Расчет потокораспределения в кольцевой сети с регуляторами расхода. На рис. 6.21 показана схема сети, состоящей из одного кольца. Вода поступает со станции в узел 0 и распределяется по участкам I—IV магистрали между абонентами 1,2 м3. Расходы воды К), К2 и К3 у абонентов заданы и поддерживаются постоянными с помощью регуляторов расхода. Суммарный расход воды К = = К] + К2 + Vy Требуется рассчитать распределение расходов воды по участкам магистрали. Условимся: а) приток воды в узел считать положительным, а сток воды из узла — отрицательным; б) потерю напора потока, протекающего в контуре по часовой стрелке, считать положительной, а потока, протекающего в контуре против часовой стрелки, — отрицательной. При вышеуказанных условиях можно следующим образом сформулировать уравнения Кирхгофа в применении к тепловой сети. Первое уравнение Кирхгофа. Алгебраическая сумма расходов воды в любом узле равна нулю: ZK=0. (6.44) Второе уравнение Кирхгофа. Алгебраическая сумма потерь напора для любого замкнутого контура равна нулю: ЬИ2=0. (6.45) Зададимся произвольным распределением расходов воды по участкам, удовлетворяющим первому уравнению Кирхгофа, И=И + Ий Hi = И + Ип; Hv = Hi - Ин. (6.46) (индекс римскими цифрами обозначает расход на участке магистрали, арабскими — на ответвлениях к абоненту). По второму уравнению Кирхгофа определим невязку потерь напора (перепада давления) в кольце 1-11-I1I-IV 8р=ЕгГ2=51Г12+5„Г2 +5ШК2, -s,vr2v> (6-47) где jj, slv — сопротивления соот ветствующих участков магистрали тепловой сети. Положительная невязка показывает, что перегружены участки, в которых расход направлен по часовой стрелке, и недогружены участки, в которых расход направлен против часовой стрелки. В данном случае применительно к рис. 6.21 положительная невязка потерь напора (перепада давлений), т.е. 8р > 0, означает, что Л/?] + А/?], + ДрП1 > Др1У или ДЯ] + ДЯ„ + ДЯц] > ДЯ|у (Дрр Дрп, АРпр Др,У — потери давления, а ДЯ,, Д#ц, А7/,„, ДН[У — падение напора на участках 1—IV магистральной кольцевой сети). При указанных условиях пьезометрический график магистральной кольцевой сети имеет вид, показанный на рис. 6.22 штриховой линией. Как видно из рис. 6.22, располагаемый напор в узле 3 кольцевой сети (см. рис. 6.21) в потоке, движущемся по часовой стрелке, т.е.в положительном потоке, = Но -МЦ- 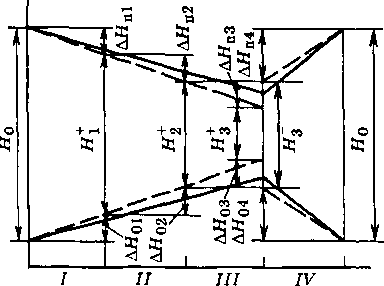 Рис. 6.22. Пьезометрический график кольцевой сети при предварительном распределении расхода воды; после учета увязочного расхода - ДЯ2 - Д#з меньше располагаемого напора в этом же узле кольцевой сети в отрицательном потоке, т.е. потоке, движущемся против часовой стрелки, = Hq- &Н4. Для того чтобы в точке водораздела располагаемые напоры в положительном и отрицательном потоках совпали, необходимо снизить в положительном потоке расход воды на какую-то величину 8 К называемую увязочным расходом, и прибавить на такую же величину 8К расход воды в отрицательном потоке. Увязочный (поправочный) расход может быть определен по уравнению (6.47), если принять в нем 8р = 0 и ввести значение увязочного расхода в правую часть уравнения. В этом случае уравнение принимает вид *,(И, - 8И)2 + ^,(И„ - 8И)2 + *И1(Ии - 5И2 - -slv(K,v + 8 И)2 = 0. (6.48) Решая это уравнение и пренебрегая чле- 2 нами, содержащими 8К как относительно малыми, получаем 8r=8p/(2£iP). (6.49) где ZsV - SjVj + 5цК|, + 5|||К|ц + sIVKIV; XsV— всегда величина положительная, поэтому в (6.49) знак Завсегда равен знаку 8р. Определив значение 8К уточняют расходы на участках и вновь проводят проверочный расчет. Обычно вполне удовлетворительные результаты получаются после второй поправки. После введения поправки пьезометрический график кольцевой сети принимает вид, показанный на рис. 6.22 сплошной линией. При большом значении увязочного расхода 8Г может измениться и предварительно принятая точка водораздела. Так, если в рассмотренном примере 8 V> VIU, то точка водораздела может переместиться из узла 3 в узел 2. Расчет потокораспределения в многокольцевых сетях с регуляторами расхода. На рис. 6.23 показана схема трехкольце- 237 Электронная библиотека http://tgv.khstu.ru/ |
