Теплофикация и тепловые сети. И тепловые

• Название: И тепловые
• Анкор: Теплофикация и тепловые сети
• Дата: 27.03.2022
• Размер: 2.4 Mb.
• Имя файла: Теплофикация и тепловые сети.docx
• Тип: Учебник; #420164
• страница: 60 из 101

Рис. 9.23. Схема напряжений в сгенках трубопро­вода под действием внутреннею давления
а₄ — под действием собственного веса трубопровода, веса тепловой изоляции и ве­са теплоносителя. В надземных теплопро­водах возможен также изгиб под действием скоростного напора ветра;

о₅ — под действием термической дефор­мации в гнутых компенсаторах и на участ­ках естественной компенсации.

Напряжения о₄ и о₅ возникают в плос­кости, нормальной к оси трубы, и векторы напряжений направлены по образующим цилиндра.

При термической деформации простран­ственных трубопроводов возникает в ряде случаев напряжение кручения т.

Перейдем к расчету усилий и напряже­ний, действующих в трубопроводах тепло­вой сетей.

Введем следующие условные обозначе­ния: р — внутреннее давление в трубопро­воде, Па; Р — осевая сила, Н; М— изгибаю­щий момент, Н • м (1 Н • м = 10,2 кгс • см); М_к — крутящий момент, Н • м; d_H — наруж­ный диаметр трубы, м; е/_в — внутренний диаметр трубы, м; 8 — толщина стенки тру­бы, м; /_т = п(₈ + 8)8 — площадь торцевого сечения трубы, м ; Е — модуль продольной упругости, для стали £= 19,6 • Ю¹⁰ Па; G— модуль сдвига, для стали G = 7,85 • 10¹⁰ Па; J - 0,05(б/⁴ _ j^) — экваториальный момент

инерции трубы, м⁴; W= 0,1 (o'⁴- d⁴)/_H — экваториальный момент сопротивления тру­бы, м³; J_n = 0,1 (⁴ - ⁴) — полярный момент

инерции трубы, м⁴; W_n = 0,2(⁴- d^)/d_H — полярный момент сопротивления трубы, м³; о — наряжение, Па.

При одновременном действии всех ви­дов деформации — при растяжении, изгибе и кручении — приведенное максимальное напряжение

% = Л²р ⁺ °и ⁺ ^²> (⁹-3)

где ст_р — суммарное напряжение растяже­ния от внутреннего давления; ст_и — суммар­ное напряжение от изгиба.

Приведенное напряжение не должно превосходить допускаемое для наиболее опасного сечения трубопровода, которым является сварной стык.

Следовательно,

ст_пр < ф [ст], (9.4)

где [ст] — допускаемое напряжение; ф — ко­эффициент прочности сварного стыка.

Напряжение растяжения в трубопроводе под действием внутреннего давления опре­деляется следующим образом. Осевая сила внутреннего давления, действующая в тор­цевой плоскости, нормальной к оси трубы

Р, =рПб/²_в/4. (9.5)

Напряжение растяжения в торцевой плоскости с вектором, направленным по об­разующей цилиндра,

^d_B

ст ₌ ! = _р 5 .(9.6)

¹ л(б/_в + 5)5 4(1 + 5/_в)5

Значение 5 /с/₈ в тепловых сетях изменя­ется от 0,05 для трубопроводов малого диа­метра (б/_в = 50 мм) до 0,01 для трубопроводов большого диаметра (б/_в = 1400 мм). Пренеб­регая 5/ d_B вследствие его малости по сравне­нию с 1, можно расчетное выражение для оп­ределения ст, записать в следующем виде:

ст, =рб/_в/(45). (9.6а)

Следует иметь в виду, что сила Р, дейст­вует не при всех схемах трубопроводов. На участках, где сила Р, = 0, напряжение ст, = 0. Такие условия имеют, например, мес­та на участках прямолинейных трубопрово­дов при установке на них сальниковых ком­пенсаторов (см. схему 1 на рис. 9.29).

Напряжение растяжения в осевой плос­кости с вектором, направленным по дуге ок­ружности, может быть определено по сле­дующей формуле, составленной для участ­ка трубы длиной /:

п₂ = = Pdj/W = pd_B/(2$), (9.7)

где Р₂ -pd_Bl — сила внутреннего давления, действующая в осевой плоскости; f_Q— пло­щадь сечения стенок трубы в осевой плоско­сти: /₀ = 25/.

Напряжение сжатия ст-, = р значительно меньше напряжений ст, и ст₂. Поэтому при расчете трубопроводов тепловых сетей ве­личиной ст₂ обычно пренебрегают.

Суммарное напряжение от растяжения под действием внутреннего давления оп­ределяется по энергетической теории прочности:

/

2 2 pd_a

о_р = 7а,₊о₂-о,о₂ = —.(9.8)

Для участков, на которых Р, = 0, а следо­вательно, ст, = 0,

^сг_р ^{= сг}2=Р^/(28). (9.8а)

Из сравнения (9.8) и (9.8а) видно, что в трубопроводах, испытывающих осевую силу внутреннего давления, напряжения в стенке ст_р на 15 % меньше, чем в трубопро­водах, где эта сила не действует. Такой на первый взгляд парадоксальный вывод объ­ясняется тем, что потенциальная энергия деформации формы, являющаяся по энерге­тической теории мерой прочности материа­ла, получается меньше, когда напряжение растяжения действует в двух взаимно пер­пендикулярных плоскостях, а не в одной плоскости.

Формулы (9.5)—(9.8) относятся к усло­виям, при которых давление в трубопрово­де постепенно возрастает от 0 до р.

В некоторых случаях, например при гид­равлическом ударе (см. § 6.8), давление в трубопроводе возрастает на величину р_у практически мгновенно.

Возникающие при этом напряжения в трубопроводе вдвое больше, чем при по­степенном повышении давления. Это объ­ясняется тем, что при мгновенном возник­новении нагрузки потенциальная энергия деформации вдвое больше, чем при посте­пенном повышении нагрузки.

Если до гидравлического удара давление в трубопроводе было равно р_н и в результа­те гидравлического удара давление повыси­лось на р_у, то при расчете напряжений в трубопроводе на растяжение ст,, ст₂ и ст_р по (9.5)—(9.8) следует принимать расчетное давление в трубопроводе

Р ⁼ Рн ^{+ 2}Ру <⁹-⁹)

Суммарное напряжение от изгиба

= J⁰* ^{+ ст}5 • (^9Л°)

Крутящие моменты возникают только в пространственных трубопроводах. В пло­скостных трубопроводах крутящие момен­ты равны нулю.

В этом случае приведенное максималь­ное напряжение

% = ⁺ (^9П)

Так как ^ст_р + ст„ < ст_р + ст_и, то из (9.11)

следует, что приведенное напряжение при одновременном действии растяжения и из­гиба меньше арифметической суммы напря­жений, возникающих в трубопроводе при раздельном действии этих деформаций.

3. 
   ОПОРЫ
   

Опоры являются ответственными дета­лями теплопровода. Они воспринимают усилия от трубопроводов и передают их на несущие конструкции или грунт. При со­оружении теплопроводов применяют опо­ры двух типов: свободные и неподвижные.

Свободные опоры воспринимают вес трубопровода и обеспечивают его свобод­ное перемещение при температурных де­формациях.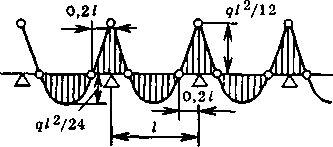



Рис. 9.24. Эпюра изгибающих моментов миогоиро- летиого трубопровода

Неподвижные опоры фиксируют поло­жение трубопровода в определенных точ­ках и воспринимают усилия, возникающие в местах фиксации под действием темпе­ратурных деформаций и внутреннего давления.

При бесканальной прокладке обычно от­казываются от установки свободных опор под трубопроводами во избежание неравно­мерных просадок и дополнительных изги­бающих напряжений. В этих теплопрово­дах трубы укладываются на нетронутый грунт или тщательно утрамбованный слой песка.

При расчете изгибающих напряжений и деформаций трубопровод, лежащий на свободных опорах, рассматривается как многопролетная балка. На рис. 9.24 приве­дена эпюра изгибающих моментов много­пролетного трубопровода.

Рассмотрим усилия и напряжения, дейст­вующие в трубопроводах. Примем следую­щие обозначения: М — силовой момент, Н • м; Q_B, Q_r — усилия вертикальное и гори­зонтальное, Н; q_B, q_r— удельная нагрузка на единицу длины вертикальная (учитывающая вес трубопровода с теплоносителем и тепловой изоляцией) и горизонтальная (учитывающая ветровое усилие), Н/м; 7V — горизонтальная реакция на опоре, Н.

При одинаковой длине пролета между свободными опорами максимальный изги­бающий момент в многопролетном трубо­проводе возникает на опоре:

M₀ = q/²/12, (9.12)

где q — удельная нагрузка на единицу дли­ны трубопровода, Н/м, / — длина пролета между опорами, м

Удельная нагрузка

Я = и ⁺ Я²_г> (9 13)

где q_r— горизонтальная удельная нагрузка, учитывающая ветровое усилие,

<7_r = *(w_B/2)pcf_H, (9 14)

Здесь w_B — скорость ветра, м/с, р — плот­ность воздуха, кг/м³, d_H — наружный диа­метр изоляции трубопровода, м, к — аэро­динамический коэффициент, в среднем рав­ный 1,4—1,6

Ветровое усилие должно учитываться только в надземных теплопроводах откры­той прокладки

Изгибающий момент, возникающий в середине пролета,

М_п =

На расстоянии 0,21/ от опоры изгибаю­щий момент равен нулю

Максимальный прогиб имеет место в се­редине пролета

Стрела прогиба трубопровода, м,

Т ⁼ <у/⁴/(384£7) (9 16)

Пролет между свободными опорами оп­ределяется с помощью (9 12)

М_о = ₄ W, (9 17) откуда длина пролета, м,

/ = jYla^W/q (9 17а)

Предварительную оценку расстояния между опорами можно произвести на осно­ве (9 17а), принимая напряжение от изгиба о₄ равным 0,4—0,5 допускаемого напряже­ния о₄ = Рф [о], где Р = 0,4—0,5

В приложениях 11 и 25 приведены ос­новные данные для расчетов нагрузок на опоры и размеры пролетов между свобод­ными опорами

-а-Ц 1