Теплофикация и тепловые сети. И тепловые

• Название: И тепловые
• Анкор: Теплофикация и тепловые сети
• Дата: 27.03.2022
• Размер: 2.4 Mb.
• Имя файла: Теплофикация и тепловые сети.docx
• Тип: Учебник; #420164
• страница: 63 из 101

Рнс. 9.38. Коэффициент жесткости гладких кривых труб

гнутых гладких отводов зависит от геомет­рической характеристики отвода, опреде­ляемой по формуле

А = 5Л/г²_ср, (9.38)

где 5 — толщина стенки трубы; г_ср — радиус изгиба оси трубы; (с/_н — 8)/2 — средний ради­ус трубы; — наружный диаметр трубы.

При h < 1 коэффициент жесткости вы­числяется по формуле Кларка и Рейснера

к = hl 1,65; (9.39)

при h > 1 — по формуле Кармана

п. — . \⁷ '^а)

10 + 12 А²

Кривая коэффициентов жесткости глад­ких труб приведена на рис 9.38.

Для прямой трубы R = оо, А = оои£ = 1. С увеличением диаметра трубы уменьша­ются коэффициент жесткости гладких отво­дов h и коэффициент жесткости трубы к. Если жесткость прямого участка трубопро­вода равна EJ, Па, то жесткость кривого участка равна kEJ, Па. Поправочный ко­эффициент напряжения для гнутых глад­ких труб

ш = 0,9/(й^2/3) (9.40)

и учитывается только при m > 1, т.е при А <0,85.

Для определения напряжений и компен­сирующей способности симметричных кон­фигураций трубопроводов, в которых пря­мая, соединяющая смежные неподвижные

опоры, совпадает с осью трубопровода, удобно пользоваться следующим упрощен­ным методом, основанным на теории изги­ба кривого бруса [78]. По этой теории зави­симость между действующим усилием и де­формацией трубопровода может быть пред­ставлена следующим выражением:

\EJ

s 2

(У tb

где Р — сила, вызывающая деформацию [направление действия силы определяется прямой, соединяющей неподвижные конце­вые точки трубопровода (рис. 9.39)]; Д — деформация по направлению действующей силы, м; у — расстояние от середины эле­ментов участка трубопровода до направле­ния действующей силы, м; dr — длина эле­мента участка, м.

При сложных конфигурациях трубопро­вода, когда аналитическое определение ry²d5

К— встречает затруднения, можно ис-

к

пользовать графический метод.

Вычерчивают а масштабе контур трубо­провода и делят периметр его на равные по длине отрезки (рис. 9.39). Длина каждого участка равна ds, а расстояние по перпенди­куляру от середины каждого участка до прямой, соединяющей неподвижные опоры трубопровода, равно _у. Значение к опреде­ляется для каждого участка по (9.39);

„ г у² ds

принимают равной I- .

к к

Изгибающий момент, возникающий в отдельных элементах трубопровода, мо­жет быть найден как произведение силы на расстояние от данного элемента до направ­ления действия силы: М = Р_у.

Возникающие в трубопроводе напряже­ния от продольного изгиба

= (9.42)

где т — поправочный коэффициент напря­жения (9.40).

После соответствующих преобразова­ний выражение для напряжения от продоль­ного изгиба в элементах трубопровода при­водится к виду

с ₌ “Л2! ₍₉

2,

2f^

^J к

где d — наружный диаметр трубопровода.

Максимальное напряжение возникает в элементе трубопровода, находящемся на наибольшем расстоянии от направления действия силы, т.е. у = у_тах.

При заданном значении допускаемого напряжения можно на основании (9.43) по­лучить выражение для компенсирующей способности компенсатора

2ст}^ о ^к

Д = —² . (9.44)

^Edm_maxy

Допускаемое напряжение для расчета компенсирующей способности определяют для конкретных схем и режимов работы трубопроводов из условия, что приведен­ное суммарное напряжение от всех видов деформаций в опасном сечении не превос­ходило допускаемого значения ф [ст].

Предварительно можно принимать до­пускаемое напряжение изгиба от естествен­ной компенсации ст = (0,3—0,4) [ст].

Компенсирующая способность компен­саторов может быть увеличена вдвое при предварительной растяжке их во время мон­тажа на величину, равную половине тепло­вого удлинения трубопровода.

На основе вышеизложенной методики получены уравнения для расчета макси­мального изгибающего напряжения и ком­пенсирующей способности симметричных компенсаторов различного типа.

Расчет П-образных компенсаторов. Мак­симальное изгибающее напряжение в П-образ- ном компенсаторе (рис 9 40)

a = EEdlmlA, (9 45)

где

Л = 2{ 1/Jfc[3,14/? /²-2,28R²l + 1,4/?³] +

+ 0,67/³ + /,/² - 4/?/² + 2/?²/- 1,33/?³}

Это максимальное изгибающее напряжение возникает в так называемой спинке компенсато­ра (участок 4—5), так как она находится на мак­симальном расстоянии от направления дейст­вующей силы Р (у_тах = /)

При предварительной растяжке компенсато­ра на половину теплового удлинения трубопро­вода компенсирующая способность

Д = 2стЛ / (Edlm) (9 46)

При установке на компенсаторе жестких свар­ных (негнутых) отводов, в которых сплющивание сечения при изгибе не имеет места, к = 1, т = 1

Расчет S-образных компенсаторов. Макси­мальное изгибающее напряжение в S-образном компенсаторе (рис 9 41), а также компенсирую­щая способность при предварительной растяжке на половину теплового утлннення трубопровода определяются по формулам (9 45) и (9 46) Для этих компенсаторов коэффициент Л определяет­ся по формуле

А = 2{ \!к [6,28/? Z² - 4,56/?²/ + 2,1 /?³] + 1.3З/³ +

+ Z,/²-8/?Z² + 4/?²Z-2/?³} (9 47)

Расчет П-образных компенсаторов. Мак­симальное изгибающее напряжение в П-образ- ном компенсаторе (рис 9 42)

При предварительной растяжке П-образного компенсатора на половину теплового удлинения теплопровода его компенсирующая способность вычисляется как

Д= 18,8ст/?/(£ЛпД) (9 49)

Расчет несимметричных конфигураций.

Для расчета максимального изгибающего напря­жения, возникающего в трубопроводе с угловой конфигурацией (рис 9 43), А П Сафоновым предложена формула [92]

1,5Д£

,² в I cosf)

где Д — удлинение короткого плеча, Z — длина короткого плеча, п = 1_ХП — отношение длины длинного плеча к длине короткого, Р = ф - 90 ⁰

При ф = 90 ⁰ или р = 0

ст= 1,5ДЕб/(л+I)//² (9 51)

Максимальное напряжение возникает в коротком плече в месте защемления у непод­вижной опоры

Приведенные формулы не учитывают сни­жения жесткости из-за сплющивания сечения и сопротивления свободных опор

При несимметричных конфигурациях трубо­проводов длины прямолинейных участков обыч­но значительно превышают радиусы гнутья отводов, поэтому неучет коэффициента Кармана не приводит к существенным погрешностям

Пространственные трубопроводы. В пространственных трубопроводах кроме деформаций растяжения и изгиба, имею­щих место в плоскостных трубопроводах, возникают деформации кручения.

На рис. 9.44 показана схема пространст­венного трубопровода. При нагревании тру­бопровода в плече АВ возникает деформа­ция кручения, вызываемая термическим уд­линением плеча CD. Аналогичная деформа­ция кручения возникает и в плече CD, вы­званная термическим удлинением плеча АВ.

Максимальное напряжение кручения возникает в концевых сечениях трубопро­водов (сечения у отвода В и С), на которые передаются крутящие моменты. Это напря­жение определяется по формуле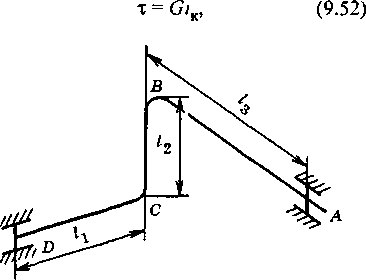



Рис. 9.44. Схема простраиствеииого трубопровода
где G — модуль сдвига, /_к — относительное кручение,

i_K = 4>r/l, (9.53)

здесь ф — угол поворота сечения трубопро­вода, рад; г — наружный радиус трубы, / — длина плеча трубопровода

Так, если при нагревании трубопровода (см рис. 9 44) участок /₃ удлинится на Д₃, то угол поворота крайнего сечения участка DC составит ф = Д₃//₂, а относительное круче­ние сечения участка DC (вблизи отвода С)

/_к = гД₃/(/,/₂). (9.54)

Аналогично относительное кручение для сечения В участка АВ

где Д| — термическое удлинение участка /,.

Как видно из (9 52) и (9 53), напряжение кручения не зависит от толщины стенки трубопровода

Крутящий момент

М_к = т(У_п, (9 56)

где W_n — полярный момент сопротивле­ния трубы.

Контрольные вопросы и задания

1. 
   В чем заключаются основные требования к конструкциям современных теплопроводов⁹
   
2. 
   Назовите современные методы защиты подземных теплопроводов от наружной коррозии
   

3. Каковы основные методы защиты подзем­ных теплопроводов от коррозии под дейст­вием блуждающих токов⁹

4. 
   Сравните подземные теплопроводы в про­ходных каналах, непроходных и бесканаль- ных Назовите преимущества и недостатки каждого типа теплопровода и основные об­ласти их целесообразного применения
   
5. 
   По каким мотивам ограничен максимальный диаметр бесканальных теплопроводов преж-
   

них конструкций? При каких условиях воз­можен отказ от такого ограничения?

6. 
   Каковы основные требования к теплоизоля­ционным конструкциям теплопроводов?
   
7. 
   Дайте характеристику бесканальных тепло­проводов с монолитной оболочкой из ячеи­стого полимерного материала типа пенопо­лиуретана с замкнутыми порами и инте­гральной структурой.
   
8. 
   В чем заключается особенность интеграль­ной структуры теплоизоляционного слоя из ячеистого полимерного материала?
   
9. 
   Каковы основные требования к трубам для теплопроводов?
   
10. 
    В чем состоит метод суммирования напря­жений в стенке трубопровода при одновре­менном действии деформаций растяжения, изгиба и кручения?
    
11. 
    Приведите расчетную формулу для опреде­ления результирующего усилия, действую­щего на неподвижную опору теплопровода.
    
12. 
    Какие усилия и напряжения возникают в за­щемленном участке трубопровода при изме­нении температуры?
    
13. 
    В чем состоит особенность компенсации те­пловых деформаций бесканальных тепло­проводов?
    
14. 
    Укажите зависимость между действующим усилием и компенсирующей способностью симметричных конфигураций трубопрово­дов. Приведите расчетную формулу и объяс­ните значения входящих в нее величин.
    

ГЛАВА ДЕСЯТАЯ

ТЕПЛОВОЙ РАСЧЕТ

1. 
   ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ
   

В задачу теплового расчета входит ре­шение следующих вопросов:

1. 
   определение тепловых потерь тепло­провода;
   
2. 
   расчет температурного поля вокруг теплопровода, т.е. определение температур изоляции, воздуха в канале, стен канала, грунта.
   
3. 
   расчет падения температуры теплоно­сителя вдоль теплопровода;
   
4. 
   выбор толщины тепловой изоляции теплопровода.
   

Количество теплоты, проходящей в еди­ницу времени через цепь последовательно соединенных термических сопротивлений, вычисляется по формуле

q = (x-t₀)/R, (10.1)

или

т -1₀ = qR\ (10.2)

Л = (т-1₀)/₉, (Ю.З)

где q—удельные тепловые потери теплопро­вода; т — температура теплоносителя, °C; /₀— температура окружающей среды, °C; R— суммарное термическое сопротивле­ние цепи теплоноситель — окружающая среда (термическое сопротивление изоля­ции теплопровода).

При тепловом расчете тепловых сетей приходится обычно определять тепловые потоки через слои и поверхности цилиндри­ческой формы.

Удельные тепловые потери q и термиче­ские сопротивления R относят обычно к единице длины теплопровода и измеряют их соответственно в Вт/м и м • К/Вт.

В изолированном трубопроводе, окру­женном наружным воздухом, теплота должна пройти через четыре последова­тельно соединенных сопротивления: внут­реннюю поверхность рабочей трубы, стен­ку трубы, слой изоляции и наружную по­верхность изоляции. Так как суммарное со­противление равно арифметической сумме последовательно соединенных сопротивле­ний, то

R = Л_в + Я_тр + Л_и + R_H, (10.4)

где /?_в, /?_тр, /?_и и R_H — термические сопро­тивления внутренней поверхности рабочей трубы, стенки трубы, слоя изоляции и на­ружной поверхности изоляции.

В изолированных теплопроводах основ­ное значение имеет термическое сопротив­ление слоя тепловой изоляции.

В тепловом расчете встречаются два ви­да термических сопротивлений:

а) сопротивление поверхности, в рас­смотренном примере R_B и /?_н;

б) сопротивление слоя, в рассмотренном примере Я_тр и Я_и.

Термическое сопротивление поверх­ности. Как известно из курса «Теплопере­дача» [46, 133, 134], термическое сопротив­ление цилиндрической поверхности

Д=1/(я<Ах), (10.5)

где nd— площадь поверхности 1 м длины

теплопровода, м²; а — коэффициент тепло­отдачи от поверхности

Для определения термического сопротив­ления поверхности теплопровода необходи­мо знать две величины: диаметр теплопрово­да и коэффициент теплоотдачи поверхности. Диаметр теплопровода при тепловом расчете является заданным. Коэффициент теплоот­дачи от наружной поверхности теплопрово­да к окружающему воздуху представляет со­бой сумму двух слагаемых — коэффициента теплоотдачи излучением а_л и коэффициента теплоотдачи конвекцией а_к:

а=а_л + а_к. (10.6)

Коэффициент теплоотдачи излучением а_л может быть подсчитан по формуле Сте­фана—Больцмана:

/Г + 273Э Эо ^{+ 273}Э

,1 100 ) I 100 J где С — коэффициент излучения; t — тем­пература излучающей поверхности, °C.

Коэффициент излучения абсолютно черного тела, т.е. поверхности, которая по­глощает все падающие на нее лучи и ниче­го не отражает, С = 5,7 Вт/(м² • К⁴) =

= 4,9 ккал/(ч • м² • К⁴).

Коэффициент излучения «серых» тел, к которым относятся поверхности неизоли­рованных трубопроводов, изоляционных конструкций и т.п., имеет значение 4,4—

5,0 Вт/(м² • К⁴) = 3,8—4,3 ккал/(ч • м² • К⁴). Коэффициент теплоотдачи от горизонталь­ной трубы к воздуху при естественной кон-

векции, Вт/(м • К), можно определить по формуле Нуссельта

а_к = 1,16 ^(/-г^/с/, (Ю.8)

где d— наружный диаметр теплопровода, м; /, г₀ — температуры поверхности и окру­жающей среды, °C.

При вынужденной конвекции воздуха или ветра коэффициент теплоотдачи

а_к = 4,65w°’⁷/c/°’³, (10.9)

где w — скорость воздуха, м/с.

Формула (10.9) действительна при w > 1 м/с и d> 0,3 м.

Для вычисления коэффициента теплоот­дачи по (10.7) и (10.8) необходимо знать температуру поверхности. Так как при оп­ределении тепловых потерь температура поверхности теплопровода обычно заранее неизвестна, задача решается методом по­следовательных приближений. Предвари­тельно задаются коэффициентом теплоот­дачи наружной поверхности теплопровода а, находят удельные потери q и температу­ру поверхности t, проверяют правильность принятого значения а.

При определении тепловых потерь изо­лированных теплопроводов проверочного расчета можно не проводить, так как терми­ческое сопротивление поверхности изоля­ции невелико по сравнению с термическим сопротивлением ее слоя Так, 100 %-ная ошибка при выборе коэффициента теплоот­дачи поверхности приводит обычно к ошиб­ке в определении теплопотерь 3—5 %.

Для предварительного определения ко­эффициента теплоотдачи поверхности изо-

лированного теплопровода, Вт/(м • К), ко­гда температура поверхности неизвестна, может быть рекомендована формула

а = 11,6 + 7Vw, (10.10) где w — скорость движения воздуха, м/с.

Коэффициенты теплоотдачи от теплоно­сителя к внутренней поверхности трубо­провода весьма высоки, что определяет столь малые значения термического сопро­тивления внутренней поверхности трубо­провода, которыми при практических рас­четах можно пренебречь.

Термическое сопротивление слоя. Вы­ражение для термического сопротивления однородного цилиндрического слоя легко

выводится из уравнения Фурье, которое имеет вид

1 ^2

R = — In—, (10.11) 2лЛ

где X — теплопроводность слоя; rfj, t/₂ — внутренний и наружный диаметры слоя.

Для теплового расчета существенное зна­чение имеют только слои с большим терми­ческим сопротивлением. Такими слоями яв­ляются тепловая изоляция, стенка канала, массив грунта и т.п. По этим соображениям при тепловом расчете изолированных тепло­проводов обычно не учитывается термиче­ское сопротивление металлической стенки рабочей трубы.

Термическое сопротивление изоляци­онных конструкций надземных тепло­проводов. В надземных теплопроводах ме­жду теплоносителем и наружным воздухом включены последовательно следующие термические сопротивления: внутренняя поверхность рабочей трубы, ее стенка, один или несколько слоев тепловой изоляции, на­ружная поверхность теплопровода.

Первыми двумя тепловыми сопротивле­ниями в практических расчетах обычно пренебрегают. При учете только двух по­следних термических сопротивлений теп­ловые потери надземного теплопровода оп­ределяются по формуле
Термическое сопротивление многослой­ной изоляции равно арифметической сум­ме термических сопротивлений последова­тельно наложенных слоев: R,, = /?_и1 + R₁₎₂+ +... + R_lw.

Термическое сопротивление цилиндри­ческой изоляции увеличивается с увеличе­нием отношения ее наружного диаметра к внутреннему. Поэтому в многослойной изоляции первые слои целесообразно укла­дывать из материала, имеющего более низ­кую теплопроводность, что приводит к наиболее эффективному использованию изоляционных материалов.

К такому же выводу приводит диффе­ренциальный анализ термического сопро­тивления многослойной (например, двух­слойной) изоляции.

Если изоляционная оболочка заданным на­ружным диаметром D_H выполнена из двух раз­личных теплоизоляционных материалов с тепло­проводностями Xi и Л₂, то тепловое сопротивле­ние такой изоляционной оболочки

D_H

In—, (10 14) D,


1

л * 2л₂
где D_T, /2,, Z2_H — наружные диаметры соответст­венно трубопровода, первого слоя изоляции, изоляционной оболочки.

Первая производная термического сопротив­ления по диаметру первого слоя

«и ^{+ Л}н


(10.12)


dR ₌ 1 П _ 1

dD, 2 л/2, U, Х₂.


(10.15а)

Если теплопровод не изолирован, то Л_и = 0. В этом случае

₉ = (t-Z₀)/R_h. (10.13)

Иногда тепловую изоляцию выполняют многослойной, исходя из различных допус­тимых температур для применяемых изоля­ционных материалов или из экономических соображений с целью частичной замены дорогих материалов изоляции более де­шевыми.
Как видно из (10.15а), приХ| <Х₂ dR/dD_t >0.

Это значит, что при выполнении первого слоя изоляции из материала с более низкой теплопро­водностью термическое сопротивление изоля­ционной конструкции увеличивается с ростом толщины этого слоя Наоборот, при выполне­нии первого слоя из материала с более высокой теплопроводностью (X, > Х₂) термическое со­противление изоляционной конструкции снижа­ется с ростом толщины первого слоя, так как в этом случае dR /dD_t < 0.

При замене бесконечно малых величин ко­нечными уравнение (10 15а) можно представить в следующем виде.


изоляции. Уравнение теплового баланса имеет вид


AR


^А£>1 J_ М _ J_ D, 2л vXj Л₂-


(10.156)


И|


откуда


Из (10 156) следует, что при выполнении в двухслойной изоляции первого слоя из материа­ла с более низкой теплопроводностью (X, < Л₂) абсолютный прирост термического сопротивле­ния изоляционной оболочки прямо пропорциона­лен относительному увеличению диаметра пер­вого слоя и разности обратных значений тепло­проводности (1 /Х| - 1/Х₂).