Практическая работа. Информационные ресурсы общества. Образовательные информационные ресурсы. Работа с программным обеспечением
 Скачать 5.79 Mb. Скачать 5.79 Mb.
|
|
Основные источники (ОИ): Таблица 2б
Дополнительные источники (ДИ): Таблица 2в
Практическая работа №8 Тема: Построение и разработка алгоритмов. Цель работы: усвоить понятия алгоритма, как фундаментальное понятие информатики, способы описания, основные типы алгоритмов, освоить принципы решения задач с использованием основных алгоритмических конструкций. Студент должен знать: -1- определение алгоритма и основные конструкции алгоритмов; уметь: -1- принципы решения задач с использованием основных алгоритмических конструкций. Теоретическое обоснование. Понятие алгоритма - фундаментальное понятие. Слово "алгоритм" происходит от имени выдающегося математика средневекового Востока Мухаммеда аль- Хорезми. Им были предложены приёмы выполнения арифметических вычислений с многозначными числами. Позже в Европе эти приёмы назвали алгоритмами от латинского написания имени аль-Хорезми. В наше время понятие алгоритма понимается шире, не ограничиваясь только арифметическими вычислениями. Термин "алгоритм" стал достаточно распространённым не только в информатике, но и в быту. Под алгоритмом понимают описание какой-либо последовательности действий для достижения заданной цели. В этом смысле, например, алгоритмами можно назвать инструкцию по использованию кухонного комбайна, кулинарный рецепт, правила перехода улицы и пр. Для использования понятия алгоритма в информатике требуется более точное определение, чем данное выше. Алгоритмом называется организованная последовательность действий допустимая для некоторых исполнителей. Исполнителем может быть человек, группа людей, робот, станок, компьютер, язык программирования и т.д. Одно из принципиальных обстоятельств состоит в том, что исполнитель не вникает в смысл того, что он делает, но получает необходимый результат. В таком случае говорят, что исполнитель действует формально, т.е. отвлекается от содержания поставленной задачи и только строго выполняет некоторые правила, инструкции. Это важная особенность алгоритмов. Наличие алгоритма формализует процесс решения задачи, исключает рассуждение исполнителя. Использование алгоритма даёт возможность решать задачу формально, механически исполняя команды алгоритма в указанной последовательности. Целесообразность предусматриваемых алгоритмом действий обеспечивается точным анализом со стороны того, кто составляет этот алгоритм. Алгоритм - это: точное и полное описание метода решения задачи, составленное из инструкций; совокупность правил, определяющих эффективную процедуру решения любой задачи; точное предписание, определяющее последовательность действий, обеспечивающих получение требуемого результата из исходных данных; набор инструкций, описывающих порядок действия исполнителя для достижения результата решения задачи за конечное число действий. Алгоритм можно представить с помощью: графического описания (блок-схемы); словесного описания; в виде таблицы; последовательности формул; алгоритмического языка. В настоящее время четко определен перечень свойств алгоритма: дискретность - свойство, отражающее упорядоченность четко разделенных друг от друга предписаний, образующих прерывистую структуру. понятность - свойство, отражающее ориентацию составления алгоритма на исполнителя; определенность - свойство, заключающееся в том, чтобы инструкции были просты, понятны и однозначны для любого выполняющего алгоритм; результативность - свойство, заключающееся в том, чтобы за определённое (конечное) число шагов достичь желаемого результата; массовость - свойство, заключающееся в том, что алгоритм решает класс задач, различающихся только исходными данными, а не одну конкретную задачу. Наиболее понятно структуру алгоритма можно представить с помощью блок- схемы, в которой используются геометрические фигуры (блоки), соединенные между собой стрелками, указывающими последовательность выполнения действий. Приняты определенные стандарты графических изображений блоков. Например, команду обработки информации помещают в блок, имеющий вид прямоугольника, проверку условий - в ромб, команды ввода или вывода - в параллелограмм, а овалом обозначают начало и конец алгоритма. Структурной элементарной единицей алгоритма является простая команда, обозначающая один элементарный шаг переработки или отображения информации. Простая команда на языке схем изображается в виде функционального блока. Данный блок имеет один вход и один выход. Из простых команд и проверки условий образуются составные команды, имеющие более сложную структуру и тоже один вход и один выход. Структурный подход к разработке алгоритмов определяет использование только базовых алгоритмических структур (конструкций): следование, ветвление, повторение, которые должны быть оформлены стандартным образом. 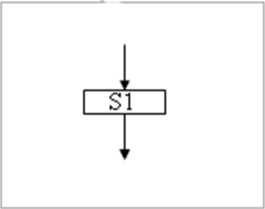  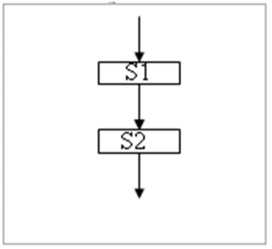 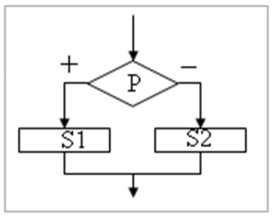 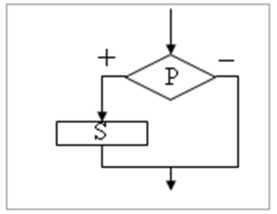 Рассмотрим основные структуры алгоритма. Команда следования состоит только из простых команд. На рисунке простые команды имеют условное обозначение S1 и S2. Из команд следования образуются линейные алгоритмы. Примером линейного алгоритма будет нахождение суммы двух чисел, введенных с клавиатуры. Команда ветвления - это составная команда алгоритма, в которой в зависимости от условия Р выполняется или одно S1, или другое S2 действие. Из команд следования и команд ветвления составляются разветвляющиеся алгоритмы (алгоритмы ветвления). Примером разветвляющегося алгоритма будет нахождение большего из двух чисел, введенных с клавиатуры. Команда ветвления может быть полной и неполной формы. Неполная форма команды ветвления используется тогда, когда необходимо выполнять действие S только в случае соблюдения условия P. Если условие P не соблюдается, то команда ветвления завершает свою работу без выполнения действия. Примером команды ветвления неполной формы будет уменьшение в два раза только четного числа. 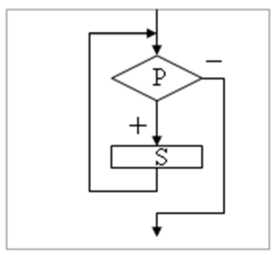 Команда повторения - это составная команда алгоритма, в которой в зависимости от условия Р возможно многократное выполнение действия S. Из команд следования и команд повторения составляются циклические алгоритмы (алгоритмы повторения). На рисунке представлена команда повторения с предусловием. Называется она так потому, что вначале проверяется условие, а уже затем выполняется действие. Причем действие выполняется, пока условие соблюдается. Пример циклического алгоритма может быть следующий. Пока с клавиатуры вводятся положительные числа, алгоритм выполняет нахождение их суммы. Команда повторения с предусловием не является единственно возможной. Разновидностью команды повторения с предусловием является команда повторения с параметром. Она используется тогда, когда известно количество повторений действия. В блок-схеме команды повторения с параметром условие записывается не в ромбе, а в шестиугольнике. Примером циклического алгоритма с параметром будет нахождение суммы первых 20 натуральных чисел. В команде повторения с постусловием вначале выполняется действие S и лишь затем, проверяется условие P. Причем действие повторяется до тех пор, пока условие не соблюдается. Примером команды повторения с постусловием будет уменьшение положительного числа до тех пор, пока оно неотрицательное. Как только число становится отрицательным, команда повторения заканчивает свою работу. С помощью соединения только этих элементарных конструкций (последовательно или вложением) можно "собрать" алгоритм любой степени сложности. Линейный алгоритм - это такой алгоритм, в котором все операции выполняются последовательно одна за другой. Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. Алгоритмы циклической структуры. Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла. Циклические алгоритмы подразделяют на алгоритмы с предусловием, постусловием и алгоритмы с конечным числом повторов. В алгоритмах с предусловием сначала выполняется проверка условия окончания цикла и затем, в зависимости от результата проверки, выполняется (или не выполняется) так называемое тело цикла. Задание 1. Определить площадь трапеции по введенным значениям оснований (а и b) и высоты (h). Запись решения задачи на алгоритмическом языке: алг трапеция вещ a,b,h,s нач ввод f,b,h s:=((a+b)/2)*h вывод s кон  Запись алгоритма в виде блок-схемы (рис. 1): 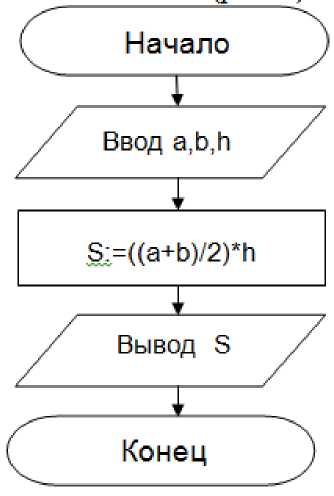 Рисунок 1. Блок-схема линейного алгоритма Задание 2. Определить среднее арифметическое двух чисел, если a положительное и частное (a/b) в противном случае. Запись решения задачи на алгоритмическом языке: алг числа вещ a,b,c нач ввод a,b если a>0 то ^=(a+b)/2 иначе ^=a/b все вывод с кон Запись алгоритма в виде блок-схемы (рис. 2):  Рисунок 2. Блок-схема алгоритма с ветвлением Задание 3. Составить алгоритм нахождения суммы целых чисел в диапазоне от 1 до 10. Запись решения задачи на алгоритмическом языке: алг сумма вещ a,s нач S:=0; A:=1; нц пока a<=10 S:=S+a; A:=a+1; кц вывод S кон Запись алгоритма в виде блок-схемы (рис. 3): 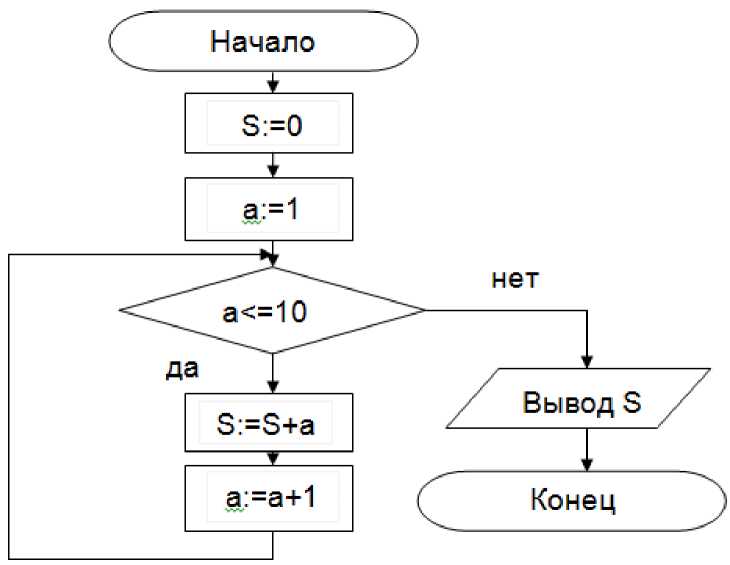 Рисунок 3. Циклический алгоритм с предусловием В алгоритме с постусловием сначала выполняется тело цикла, а затем проверяется условие окончания цикла. Решение задачи нахождения суммы первых десяти целых чисел в данном случае будет выглядеть следующим образом: алг сумма вещ a,s нач S:=0; A:=1; нц S:=S+a; A:=a+1; пока a<=10 кц вывод S кон Запись алгоритма в виде блок-схемы (рис. 4):  Рисунок 4. Циклический алгоритм с постусловием Ход работы: Изучить теоретическое обоснование. Выполнить практические задания. Оформить отчет. Ответить на контрольные вопросы. Практические задания: Задание №1. Составить алгоритм приготовления напитка на выбор. Нарисовать блок схему. Исходные данные: чайник с чаем; кофейник с кофе; молочник с молоком; чашка; ложка; сахарница с сахаром. Задание №2. Два мальчика и двое взрослых должны переправиться на другую сторону реки на плоту, который выдерживает либо двух мальчиков, либо одного мальчика и одного взрослого. Как осуществить переправу? Найдите несколько способов решения этой задачи. Алгоритм решения задачи:
Обозначения: 1м- один мальчик, 2м - два мальчика, 1в - один взрослый. Задание №3. Задан треугольник со сторонами a, b и с. Составить блок-схему алгоритма вычисления радиуса описанной окружности. Решение. Опишем алгоритм решения данного задания на словесном уровне. Входные данные: стороны а, b, с треугольника АВС. Переменная S используется для площади треугольника, р - для полупериметра треугольника, R - для радиуса описанной окружности. Для вычисления используются формулы: (а+Ь+с) р = — полупериметр треугольника; S = ^р(р — а)(р — Ь)(р — с)- формула Герона для вычисления площади треугольника; аЬс к = радиус описанной окружности треугольника. 4.S Вывод R. Задание №4. Составить блок-схему вычисления функции знака ( 1, если х > 0 0, если х = 0 — 1, если х < 0 где x - заданное вещественное число. Решение. Опишем алгоритм решения данного задания на словесном уровне. Входные данные: переменная х. Проверяется введенное значение переменной х. В зависимости от введенного значения функция F принимает одно из значений: 0, 1 или -1. При вводе неверного значения (буква, слово) программа выдает сообщение «это слово». Вывод значения. Задание №5. Составить блок-схему вычисления и вывода на печать значения а" функции у = вводится с клавиатуры при выполнении программы. Решение. Опишем алгоритм решения данного задания на словесном уровне. Входные данные: переменная a. Перед первым выполнением цикла необходимо задать необходимо, задать начальное значение аргумента х, равное 0. Вычислить значение у и вывести его на печать. При каждом новом выполнении цикла необходимо изменять аргумент на величину шага, равного 0,1. Чтобы процесс не был бесконечным, необходимо задать условие повторения (х<3) или окончания цикла (х>3). Контрольные вопросы. Что такое алгоритм? Свойства алгоритма. Способы записи алгоритма. Основные элементы блок-схемы. Виды алгоритмов. Отличительные особенности алгоритмов с предусловием и постусловием. Содержание отчета: Название и цель работы. Результат выполнения практических заданий. Ответы на контрольные вопросы. Литература. Основные источники (ОИ): Таблица 2б
Дополнительные источники (ДИ): Таблица 2в
Практическая работа№9 Тема: Разработка линейного алгоритма (программы). Цель: знакомство со средой программирования Pascal; изучить структуру программы, стандартные функции, оператор присваивания и процедуры ввода-вывода; научиться создавать программы на языке Pascal с использованием стандартных функций. Студент должен знать: -1- формат линейной алгоритмической структуры; -1- базовые понятия языка программирования Pascal; -1- форматы операторов ввода вывода и присваивания; уметь: -1- составлять простую программу линейной алгоритмической структуры. Теоретическое обоснование. Алфавит языка При записи программ разрешены символы: буквы латинского алфавита А-Z (в любом регистре), а также знак подчеркивания _; буквы русского алфавита А-Я; цифры 0-9; специальные символы > < = + - / * [ ] ( ) { } . , : ; Л @ ’ $ # пары символов (их нельзя разделять пробелами) < > <= >= := (* *) (. .) пробелы (рассматриваются как ограничители идентификаторов, констант, чисел, зарезервированных слов). Идентификаторы Неделимые последовательности символов алфавита образуют слова - идентификаторы, используемые для обозначения констант, переменных, процедур, функций и т.д. Идентификатор должен начинаться с буквы или символа подчеркивания, не должен содержать пробелов и специальных символов. Константы В качестве констант могут использоваться числа, логические константы, символы и строки символов. Целые числа записываются со знаком или без него по обычным правилам и могут иметь значение от -2147483648 до +2147483647. Вещественные числа записываются со знаком или без него с использованием десятичной точки и/или экспоненциальной части. Экспоненциальная часть начинается символом е или Е, за которым могут следовать знаки «+» или «-» и десятичный порядок. Символ е (Е) означает десятичный порядок и смысл «умножить на 10 в степени». Например, запись 3.14Е5 означает 3,14 • 105 ,а запись -17е-2 - это -17- 10-2. Выражения Выражение задает порядок выполнения действий над элементами данных и состоит из операндов (констант, переменных, функций, круглых скобок и знаков операций). Действия в выражении выполняются слева направо с соблюдением старшинства (в порядке убывания): * (умножение), / (деление), div (целочисленное деление), mod (целочисленное деление с остатком по модулю), and (логическая операция “И”); + (сложение), - (вычитание), or (логическая операция “ИЛИ”); операции отношений: = (равно), <> (не равно), < (меньше), > (больше), < = (меньше или равно), > = (больше или равно). Для изменения порядка выполнения действий используются круглые скобки. Число открывающихся скобок равно числу закрывающихся. Любое выражение в скобках вычисляется раньше, чем выполняется операция, предшествующая скобкам. В выражение могут входить функции. Наиболее часто употребляемые функции называют стандартными. Для работы с ними не надо ни заказывать библиотеку, ни описывать их предварительно в программе. Примеры стандартных математических функций: ABS(x) - модуль х ( | х |); SQR(x) - квадрат числа х (х 2) ; SQRT(x) - квадратный корень из х (VX); LN(x) - натуральный логарифм от х ( Inх); LG(X) - LN(x)/ LN(10) EXP(x) - е в степени х (е); SIN(x) - синус х (sinх); COS(x) - косинус х (cosх); EXP(x*ln(k)) - k в степени х (kх); Аргумент этих функций может быть как вещественным, так и целым. Результат - всегда вещественный. Типы данных Любые данные, т.е. константы, переменные, значения функций или выражения в Турбо Паскале характеризуются своими типами. Тип определяет множество допустимых значений, которые может иметь тот или иной объект, а также множество допустимых операций, которые применимы к нему. Все типы данных разделяются на две группы - простые и составные. К простым (скалярным) типам относятся: INTEGER - данные этого типа могут принимать только целые значения (положительные, отрицательные, 0) в диапазоне от -32768 до +32767; REAL - величины этого типа могут принимать только вещественные значения (числа с дробной частью, целая часть от дробной отделяется точкой); Структура программы Структура программы должна быть такой: <Заголовок программы> {Блок описаний} BEGIN {Раздел исполняемых операторов} END. Заголовок программы В заголовке указывается имя программы. Общий вид заголовка: program n; здесь n -имя программы. Заголовок программы необязателен, его можно опускать без каких-либо последствий для программы. Блок описаний В блоке описаний объявляются идентификаторы типов, констант, переменных, а также метки, процедуры и функции. Блок описаний может состоять из пяти разделов, которые должны следовать в строго определенном порядке: раздел меток (label); раздел констант (const); раздел типов (type); раздел переменных (var); раздел процедур и функций. |
