Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
Глава 11 Создание полигонов Тиссена довольно просто концептуально, но может стать запутанным, если количество точек велико. Чтобы понять, как их строить, давайте вначале разберемся, что эти фигуры должны представлять. Если у нас есть несколько точечных объектов, таких как города (опять же, одного размера), мы можем представить себе, что каждая точка окружена одиночным неправильным многоугольником. Но многоугольник имеет одно важное свойство - любая точка внутри него находится ближе к очерченной точке, чем любая другая точка покрытия. И наоборот, каждая точка вне полигона ближе к некоторой иной, нежели к очерченной. Другими словами, граница каждого полигона дает окружаемой точке наименьшую возможную область влияния. Каждая точка покрытия будет иметь свой собственный полигон Тиссена, показывающий область исключительно ее влияния [Clarke, 1990]. Теперь давайте подумаем, как мы могли бы сделать это. Возьмем простой набор точек (Рисунок 11.3). Образование полигонов Тиссена можно представить как результат роста мыльных пузырей с центром в каждой из точек. В конце концов границы пузырей превращаются в прямые линии, а сами пузыри - в многоугольники. Стороны этих многоугольников ориентированы перпендикулярно линиям, соединяющим соседние точки. Причем длины двух отрезков, получившихся с обеих сторон границы, одинаковы. 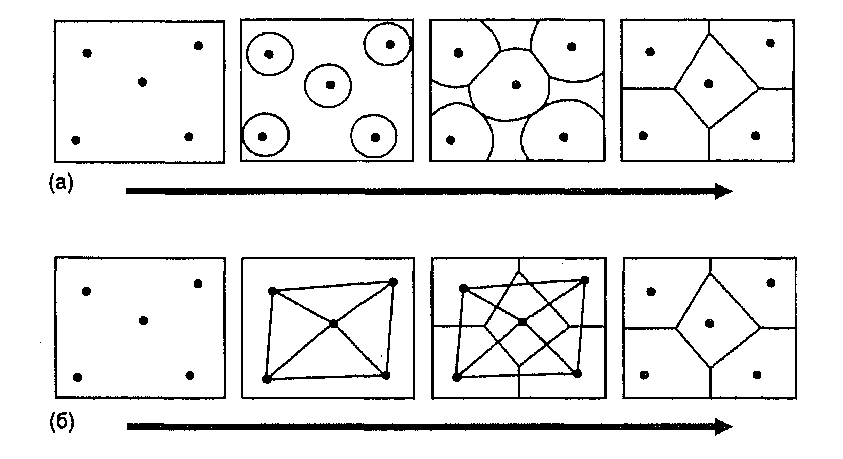 Рисунок 11.3. Создание полигонов Тиссена. а) расположение точек; b) построение связанных с ними полигонов Тиссена. Алгоритмы создания полигонов Тиссена разрабатывались на протяжении десятилетий как для систем компьютерной картографии, так и для ГИС, как векторных [Brassel and Reif, 1979], так даже и на структуре данных Пространственные распределения квадродерева [Mark, 1987]. Зачем же нужны полигоны Тиссена? Они названы в честь климатолога Тиссена (А.Н. Thiessen), который пытался проинтерполировать сильно неравномерные распределения климатических данных. Иначе говоря, он пытался описывать и анализировать точечные данные с помощью площадных символов и аналитических методов. Таким образом, если у нас есть несколько разбросанных точек, и мы хотим охарактеризовать регионы, основанные на этих точках, то используем полигоны Тиссена. Поскольку мы считаем, что в каждом полигоне влияние очерченной точки абсолютно, мы можем обращаться с этими данными как с полигональным покрытием. Большинство случаев применения полигонов Тиссена связано с определением влияния точечных данных, представляющих торговые центры, фабрики или другие объекты экономики. Если мы изменим положение общей границы смежных полигонов в зависимости от размера или иного параметра очерчиваемых ими точек, то полученное разбиение будет еще лучше представлять реальное влияние объектов на окружающее пространство. Имея такую информацию, специалист по экономическому размещению может определить, например, какая часть населения города (на основе близости) скорее всего будет регулярно посещать планируемый торговый центр. Полигоны Тиссена используется не только в экономической географии, но и, например, при выявлении пространственных распределений растительности [Hutchings and Discombe, 1986]. На самом деле, использование этой методики скорее всего будет расти с расширением функциональных возможностей ГИС и известности среди пользователей. РАСПРЕДЕЛЕНИЯ ПОЛИГОНОВ Мы можем начать анализировать распределения областей во многом подобно тому, как мы делали это с точками - через определение плотности полигонов на единицу площади нашей области изучения. Однако, при определении меры плотности полигонов мы должны вначале измерить площадь полигонов каждого класса, из тех, что интересуют нас. Затем мы делим суммарную площадь каждого типа полигонов (т.е. каждого региона) на общую площадь покрытия. Это дает относительную долю полигонов, а не число их на единицу площади. Возможно, конечно, подсчитать число полигонов (или групп ячеек растра) на единицу площади, но из-за возможности широкого варьирования их размеров данный подход вряд ли будет полезен. Опять же, помимо плотности полигонов, нас может интересовать расположение и формы распределений, создаваемые группами полигонов, которые могут подсказать причины таких расположений. Примерами потенциально взаимодействующих полигонов могут быть усовершенствования в методах вспашки в некоторых хозяйствах, города, поселки и перемещение товаров и услуг внутри них и между ними, и даже водные источники, распределенные по территории, которая могла бы предоставить хорошие места для зимовки птиц. Но перед тем, как рассматривать взаимодействия полигональных объектов, мы должны узнать кое-что о том, как они могут быть расположены. Как и точки, области могут быть сгруппированы, рассеяны (регулярно), или случайным образом разнесены по отношению друг к другу (см. Рисунок 2.8). Кроме этого, площадные объекты могут быть соединены друг с другом, или удалены на некоторые определимое расстояние. Статистик соединений При работе с полигональными покрытиями мы будем нередко создавать бинарные карты (binary maps), т.е. такие, на которых имеются только две категории полигонов, - чаще всего таких, которые характеризуют некоторый показатель как хороший или плохой для искомого решения. Например, могут быть плохие и хорошие почвы для пропашных культур, хорошие и плохие уклоны для строительства, хорошие и плохие аспекты для установки солнечных батарей. Возможность определения распределений некоторых из этих показателей может пригодиться, возможно, потому, что мы должны размещать дома, растения или солнечные батареи одной большой группой (что характерно для кластерных распределений), а не разрозненно. Мы можем также интересоваться выявлением распределения объектов определенной области, таких как размытые поверхности, сорная растительность или типы заселения для выяснения какой-нибудь возможной причины образования наблюдаемых примеров. Мы уже познакомились с понятием непосредственной окрестности на основе смежности, определяемой как условие контакта полигональных объектов друг с другом (Глава 9). Но, хотя простая мера смежности может быть полезна для рассмотрения размеров соединенных полигонов одного типа, она мало что говорит нам о распределении, образуемом этими региональными полигонами. Для этого применяется статистический показатель (статистик) соединений (общих границ). Он не связан только лишь с бинарными картами, но так как они лучше его иллюстрируют, и относительно просто перейти от многокатегориальных карт к бинарным [McGrew and Monroe, 1993] (что является обычной практикой), мы ограничимся только случаем бинарных полигональных карт. Соединение - это общая граница двух смежных полигонов. Статистик соединений подсчитывает количество соединений в полигональном распределении и характеризует структуру соединений каждого покрытия [McGrew and Monroe, 1993]. Посмотрите на Рисунок 11.4а, показывающий область с пятнадцатью полигонами, и имеющимися между ними соединениями. 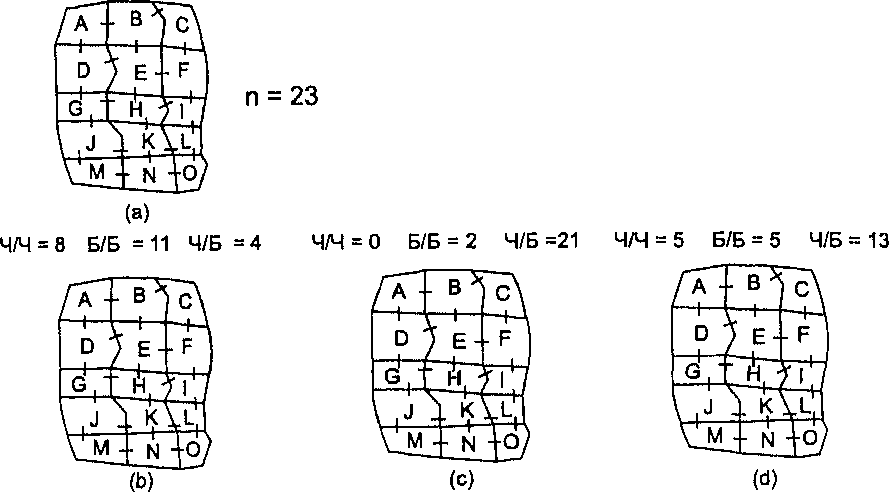 Рисунок 11.4. Статистик соединений для области из 15 полигонов: а) 23 возможные соединения, b) кластерное распределение, с) разреженное распределение, d) случайное распределение. Всего между полигонами имеются 23 соединения (т.е. общих участков границ). На Рисунке 11.4b среди них: 8 соединений между заштрихованными полигонами, 11 - между белыми и 4 - между заштрихованными и белыми. Эти числа показывают, что между заштрихованными и белыми полигонами имеется мало соединений, большинство белых полигонов соединены друг с другом, и большинство заштрихованных полигонов соединены друг с другом. Другими словами, полигоны сгруппированы, подобно тому, что мы прежде наблюдали с точками. Рисунок 11.4с показывает совершенно другой набор чисел; здесь большинство соединений (21 из 23) - между полигонами разных классов, т.е. мы имеем разреженное распределение. Рисунок 11.4d -промежуточный случай: оба числа соединений однородных полигонов низки, но не так, как на Рисунке 11.4с. Число разнородных соединений также не настолько высоко, как в случае разреженного распределения. Таким образом, здесь мы имеем дело со случайным распределением. Теперь обратимся к вопросу об использовании результатов Данного вида анализа. Мы определили числа однородных и неоднородных соединений и можем выделить три различных класса распределений. Но как в действительности сравнить результаты анализа одной БД с тем, что можно было бы ожидать при кластерном, разреженном и случайном распределениях? Главным образом, нас интересует случайность, она говорит о том, что расположение полигонов скорее всего не зависит от какой-либо причины. И наоборот - в двух других случаях такая причина наверняка существует. При анализе точечных распределений для оценки случайности мы обращались к критерию х2. Но этот показатель подразумевает, что мы знаем, каким должно быть ожидаемое распределение в условиях случайности. Если бы мы знали подобные распределения для полигонов (на основе числа соединений), то могли бы сравнивать их точно таким же способом. Но как мы узнаем ожидаемое случайное распределение соединений, с которым могли бы сравнить имеющиеся значения? Имеются два подхода к решению этой задачи. Первый, называемый свободным отбором (free sampling), предполагает, что мы можем определить ожидаемую частоту соединений внутри категорий и между ними либо на основе теоретического знания моделируемой ситуации, либо исходя, из известных распределений для больших областей исследования. В первом случае, например, мы могли бы знать, что вследствие определенных зональных установлений в городе, торговые центры или объекты промышленности встречаются с определенной регулярностью по сравнению с другими типами землепользования. И тогда мы могли бы сравнить эти распределения с регулярностью торговых областей в другом городе, чтобы увидеть, используется такое же зонирование или другое, приводящее к существенно другому распределению торговых центров и объектов промышленности по сравнению с другими типами землепользования. Во втором случае, т.е. при использовании известного распределения на большей изучаемой области, могут быть выполнены подобные же сравнения. Скажем, нам известно распределение полигональных соединений нашего округа из анализа сельхозкультур. Тогда мы могли бы рассмотреть распределение их в отдельном пригородном районе и сравнить число соединений в этой подобласти с числом соединений для всего округа, чтобы увидеть, имеется ли сходство. Второй подход, называемый несвободным отбором (nonfree sampling), применяется более часто. Он не делает теоретических предположений о распределении и не полагается на сравнение чисел соединений подобласти и всей области. В нем сравниваются числа соединений оценочного случайного распределения с числом соединений наблюдаемого распределения полигонов. Другими словами, мы создаем случайное распределение, исходя только из самих полигонов. Тогда мы можем сравнить имеющиеся результаты со случайным распределением, имея в виду отклонения от случайности, говорящие о действии некоторого причинного механизма. Как свободный, так и несвободный отбор могут дать понимание распределения, но эти вычисления выполняются чаще опытными пользователями ГИС, нежели новичками. Поэтому мы не будем здесь рассматривать детали вычислений сравнительных показателей. Впрочем, вы можете обратиться, например, к исследованиям, показывающим, как это делается по отношению к губернаторским местам Республиканцев и Демократов в восточной части США [McGrew and Monroe, 1993]. Другие меры распределений полигонов Анализ распределений полигонов может быть весьма сложным, и связи ГИС с другим программным обеспечением дают возможность выполнять его [Baker and Cai, 1992; McGarigal and Marks, 1994]. Ландшафтные экологи часто используют эти методы, обычно рассматривая полигоны как островки (patches), особенно по отношению к большему, более однородному окружению (background), так называемой матрице (matrix). Вы можете в дальнейшем обратиться к соответствующей книге [Forman and Godron, 1986} за обзором некоторых из этих методов. В общем случае вы найдете меры полигональной изолированности (polygonal isolation), меры доступности (accessibility), взаимодействий полигонов (polygon interactions) и рассредоточенности (dispersion). Поскольку многие из этих мер заимствованы из литературы по географии, биогеографии, экологии, лесоводства и других дисциплин, примеры будут достаточно разнообразны, чтобы дать вам представление о возможностях использования этих дополнительных мер. РАСПРЕДЕЛЕНИЯ ЛИНИЙ Мы встречаем линейные паттерны постоянно, но часто и пропускаем их. Улицы и шоссе образуют узнаваемый паттерн, который мы относим к сетям, создаваемым человеком для перемещения людей и вещей между пространственно распределенными точками, называемыми городами. Нам встречаются ограждения, также имеющие определенные конфигурации и количества в зависимости от размеров полей, участков, форм полигонов, которые они окружают [Simpson et al., 1994]. Полосы на открытых участках коренной породы показывают параллельные линии перемещения камней под ледником, проходившем тысячи лет назад. Механизмы, вызвавшие образование каждого из этих линейных паттернов, лучше всего могут быть поняты, если мы прежде определим конкретные параметры соответствующих распределений. Плотность линий Поскольку линии в отличие от точек имеют пространственную протяженность, анализ их распределений несколько сложнее. Одни исследователи изучали распределения длин линий [Aitchison and Brown, 1969], другие рассматривали интервалы между линиями [Dacey, 1967; Miles, 1964], во многом подобно анализу ближайшего соседа в точечных распределениях [Davis, 1986]. Мы рассмотрим эти и другие меры распределений линий в последующих параграфах, и начнем с простейшей меры - плотности линий. Мы определили плотность безразмерных точек как отношения их числа кзанимаемой ими площади. Плотность двухмерных полигонов определялась как отношение суммарной площади класса к площади всей карты. Подобным же образом, для определения плотности одномерных линий мы будем использовать отношение суммы их длин к площади покрытия. Выражаться оно может в метрах на гектар или километрах на квадратный километр. За исключением сравнения с аналогичными величинами для других регионов или для того же региона в другие моменты времени, мы мало что можем сделать с этой информацией. Поэтому сейчас мы рассмотрим другие показатели распределений линий, аналогично тому, как было с распределениями точек и полигонов. Ближайшие соседи и пересечения линий Распределение пар линий может быть определено во многом подобно тому, как мы поступали с точками, хотя вычисления несколько усложняются, так как, в отличие от точек, линии имеют размерность. Может показаться, что следует просто выбрать центр каждой линии и провести анализ ближайшего соседа для этих точек. Однако, вследствие того, что линии имеют различные длины, эта процедура не даст нам правдивой картины распределения самих линий. С точки зрения статистики часто считается полезным делать случайную выборку. Следуя этому подходу, нашей первой задачей в анализе ближайших соседей среди линейных объектов будет выбор случайной точки на каждой линии карты (или на каждом сегменте линии, если они - не прямые). Далее, опускается перпендикуляр из этой точки к ближайшей линии (Рисунок 11.5) [Davis, 1986]. Затем мы измеряем эти расстояния и подсчитываем среднее РБС. Как со всеми РБС, мы должны иметь возможность оценить эту величину по отношению к случайному распределению. Дэйси [Dacey, 1967] определил значения для ожидаемых РБС, дисперсии и стандартной ошибки случайного распределения линий. Эти величины позволяют нам сравнить ожидаемое и наблюдаемое и создать статистический показатель, по которому можно протестировать гипотезу о случайности [Davis, 1986]. По указанной ссылке можно найти описание соответствующих формул. Этот критерий работает для большинства распределений линий, будь линии прямыми или изогнутыми, но имеет и некоторые ограничения. Если линии очень извилисты, этот подход - менее чем успешен. 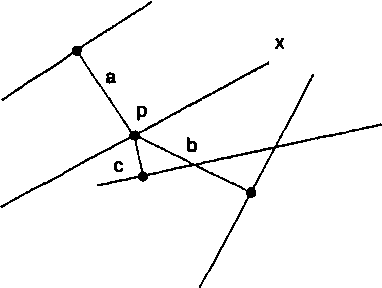 Рисунок 11.5. Расстояние до ближайшего соседа среди линий. Поиск ближайшего соседа между линиями с использованием случайно выбранной точки на одной из них. Кроме того, чтобы критерий был полезен, линии должны быть по меньшей мере в полтора раза длиннее среднего расстояния между ними. Если количество линий в покрытии мало, оценка плотности, используемая в анализе ближайшего соседа должна быть скорректирована весовым коэффициентом (n-1)/n, где n - число линий распределения. То есть, вместо отношения суммы длин на площадь мы используем формулу (n-l)L/nA, где L- сумма длин, а А - площадь. Эта скорректированная плотность линий улучшит качество статистика ближайшего соседа. Методы пересечения линий являются альтернативой при анализе распределения линий. Один простой подход состоит в том, чтобы преобразовать двухмерный паттерн в одномерную последовательность прочерчиванием выборочной линии через карту и учетом пересечений этой линии с линиями покрытия. Существуют по меньшей мере два способа создания таких линий [Getis and Boots, 1978]. Первый - случайно выбрать пару точек и соединить их линией. Второй метод состоит в проведении луча из случайной точки под случайным углом, откладывании случайного расстояния от начальной точки и проведении перпендикуляра к лучу из этой точки [Davis, 1986]. После того, как линия проведена, может быть рассмотрено распределение интервалов между пересечениями ее с линиями покрытия с использованием стандартных методов анализа наборов данных. Альтернативой одиночной линии является зигзагообразная, которая пересекает покрытие два или три раза. Зигзагообразный путь (часто называемый случайным обходом (random walk)) также создаст серию пересечений, расстояния между которыми опять же могут быть проанализированы любым статистическим методом для последовательностей данных (Рисунок 11.6). 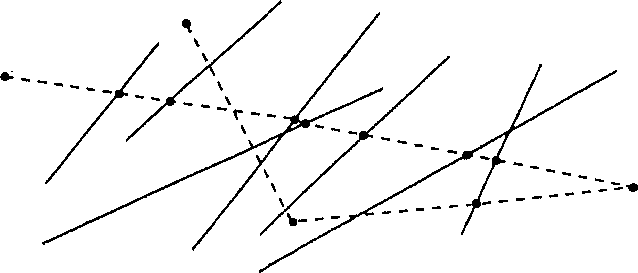 Рисунок 11.6. Метод случайного обхода для оценки распределения линий. Модификация метода пересечений с использованием зигзагообразной линии для получения точек выборки. |
