Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
Глава 10 области исследования. Но так как у нас нет данных с левой стороны границы, алгоритм будет искать соседние точки справа, сверху и снизу от интерполируемой точки на границе, и интерполируемая величина будет подвержена влиянию этих трех направлений. То есть, полученные значения могут оказаться ниже, чем те, которые находятся на смежном листе карты. Следовательно, при выполнении интерполяции появится тенденция недооценки пропущенных значений, что приведет к созданию карты поверхности, вдоль границ которой вычисления уклона, азимута, видимости, маршрута наименьшей стоимости и другие будут ошибочными. Несмотря на очевидные проблемы при выполнении вычислений поверхности в таких условиях, даже опытные пользователи ГИС попадаются в ловушку выбора точек в пределах только исходной области исследования. Иногда эта процедурная ошибка случается из-за того, что данные о поверхности не были частью первоначального замысла, иногда потому, что область исследования выбиралась на основе границ отдельной карты, а иногда из-за недостатка времени. Бывают и другие причины, но результат -тот же: сомнительная база данных (или даже база сомнительных данных;) и некорректные результаты анализа. Решение проблемы так же очевидно, как и она сама. Просто расширьте границы покрытия высот за пределы исходной области исследования (Рисунок 10.14). Нет необходимости расширять саму область исследования, чтобы удовлетворить потребность в большем количестве исходных точек. Достаточно создать покрытие, внешние границы которого шире исходной области исследования, затем провести интерполяцию, после чего опять вернуться к исходным границам, "отрезав" края (модели высот, модели уклона, области видимости и т.д.). Определение размера дополнительной площади покрытия, необходимой для получения приемлемых результатов интерполяции, - дело трудное. Теоретически, было бы полезно выполнить какого-нибудь рода анализ окрестности, возможно подобный анализу в кригинге, для выяснения, насколько далеко должны располагаться точки данных, чтобы гарантировать, что они не оказывают влияния на соседние с ними значения высот, но это требует времени. Наилучший совет -перестраховаться, расширяя область настолько, чтобы гарантировать правильность вычислений. Чаще всего достаточно расширения на 10% в каждую сторону для обеспечения хороших результатов, но при этом следует учитывать и сложность поверхности. Чем более быстро изменяется высота вблизи границ, тем больше они должны быть расширены, - чтобы уравновесить влияние соседних исходных точек, воздействующих на интерполируемые значения. Здесь нет стандартных инструкций, вам понадобится собственный опыт и знание ваших данных. Любое расширение границ улучшит качество анализа и всегда лучше, чем полное отсутствие расширения. 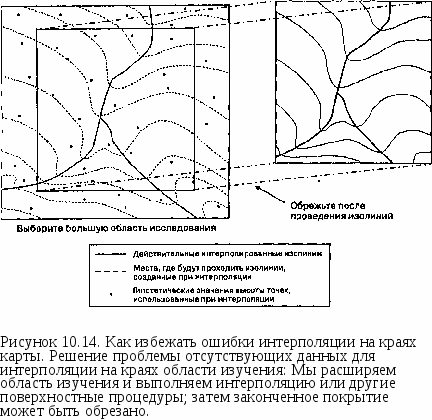 НАРЕЗКА СТАТИСТИЧЕСКИХ ПОВЕРХНОСТЕЙ Как было сказано выше, основным методом отображения информации о поверхности является использование изолиний, которые проводятся через установленные интервалы. Выбранный интервал позволяет передавать форму поверхности, при этом мы полагаем, что высота между контурными линиями изменяется непрерывным образом, так как считаем саму поверхность непрерывной. Мы также полагаем, что интервал выбирается таким, чтобы отобразить форму поверхности наилучшим образом. Большинство растровых и векторных ГИС позволяет изменять этот интервал и даже преобразовывать область каждого интервала в плоскую поверхность. Для простоты мы будем называть эту группу методов нарезкой (slicing) и представлять их выполнение как множественное рассечение поверхности по горизонтали острым ножом. Нарезка может быть просто делом выбора другого контурного интервала, позволяющего по-иному взглянуть на особенности рельефа поверхности (Рисунок 10.15). Например, мы могли бы увеличить интервал между изолиниями, чтобы выявить общую форму объектов без избыточных подробностей. Хорошая визуализация дает представление о тенденциях без необходимости реального вычисления поверхностного тренда, И наоборот, чтобы увидеть больше деталей, мы можем уменьшить вертикальный интервал между изолиниями. Конечно же, сами исходные данные должны быть при этом достаточно подробными. 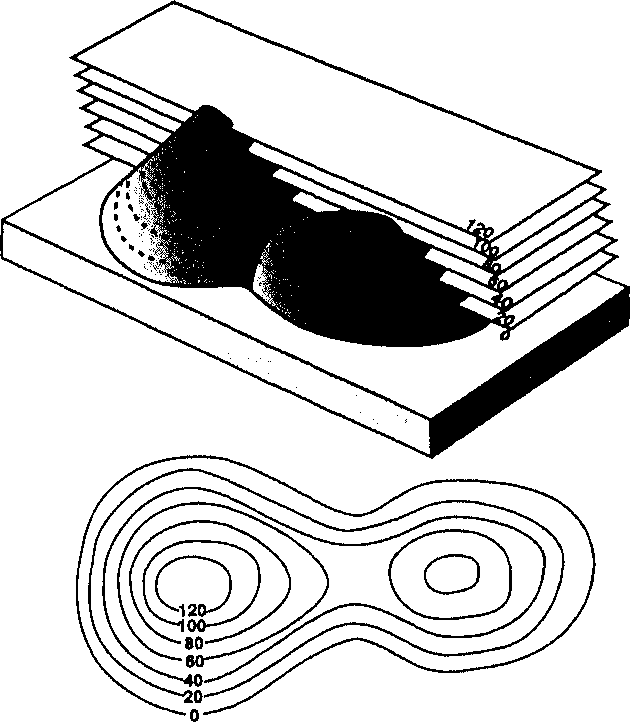 Рисунок 10.15. Нарезка Z-поверхности. В более общем случае функция нарезки могла бы правильнее называться функцией окрестности, как говорилось в Главе 9. Здесь же мы ее рассматриваем потому, что по своему выполнению она тесно связана с интерполяцией. Этот подход подразумевает, что проведением контурных линий на заданных интервалах мы по сути сводим непрерывную поверхность к дискретной, ступенчатой поверхности. Почему же мы низводим наши данные из непрерывных в дискретные? Возможно, следующий пример поможет ответить на этот вопрос. Допустим, вы работаете в консалтинговой фирме с контрактом, заключенным с правительством другой страны. И вас попросили определить подходящие виды землепользования для большого участка земли на основе комбинации характеристик почвы и классов высот. Классы высот выбирались вместо классов уклона отчасти потому, что большинство земельных изысканий учитывают уклон в характеристиках почвы, отчасти потому, что советники клиента по сельскому хозяйству знают, что некоторые растения растут на одних высотах лучше, чем на других. Исходя из требований к высоте различных сельскохозяйственных культур (таковых, скажем, - пять) вы можете разделить поверхность на пять высотных регионов нарезкой четырьмя плоскостями. После выполнения нарезки эти регионы могут быть переклассифицированы по их влиянию на те пять культур. Теперь у вас есть пять групп, основанных на высотных классах с учетом воздействия последних на сельхозкультуры, названные "высоты для культуры 1", "высоты для культуры 2" и т.д. Таким образом, вы преобразовали данные поверхности, представленные в шкале отношений (непрерывные), в данные номинальной шкалы (дискретные), исходя из воздействия высоты на культуры. Как мы увидим в Главе 12, эти результаты могут быть объединены с другими покрытиями для принятия решений о том, где какие культуры должны быть посажены. ОБЪЕМЫ, ОГРАНИЧИВАЕМЫЕ ПОВЕРХНОСТЯМИ Хотя интерполяция полезна для работы с поверхностями, она может также применяться к множеству других задач, связанных с вычислением объемов под объектами на поверхности, или объемов материала, связанного с выемками и заполнением (как, например, при изъятии руды и последующем заполнении для сохранения плоской поверхности). Во всех таких случаях требуется знание двух граничных поверхностей: верхней и нижней. Применив нарезку или методы интегрального исчисления, мы можем определить объем. Давайте посмотрим, как это делается. Если бы мы имели цилиндрический объект с площадью основания, скажем, 150 кв.м и высотой два метра, то его объем составил бы 2 х 150 = 300 кубометров. Но большинство измеряемых объектов имеют сложную форму. Рассмотрим, например, дождевые осадки. Пусть у нас есть 15 измерителей, разбросанных по площади в 100 кв.км (1 ООО ООО кв.м), и после сбора данных мы хотим определить общее количество осадков в каждом месте за целый год. Из-за изменчивости осадков, мы можем получить значения, скажем, от 50 см до 150 см. Взяв среднюю величину осадков (100 см), мы можем представить себе плоскую поверхность, и тогда получим объем в 1 м х 1 000 000 кв.м = 1 000 000 кубометров воды. 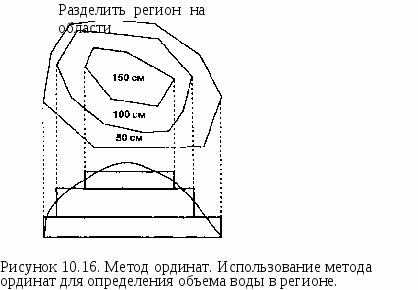 Вычислить площадь каждой области Умножить её на количество осадков Сложить эти произведения для получения общего объема осадков Но допустим, что нам нужно более точное определение объема осадков. Для этого мы можем использовать так называемый метод ординат (method of ordinates) [Muehrcke and Muehrcke, 1992]. Рисунок 10.16 показывает, как он работает. Сначала мы записываем координаты каждого измерителя осадков и создаем матрицу высот, точно так же, как мы поступали бы в случае топографии. Затем мы используем подходящий метод интерполяции для создания поверхности и режем ее на части равной толщины (т.е. проводим изолинии). Если мы примем, что стенки полученных слоев вертикальны, то сможем выполнить тот же простой расчет объема для каждого из них. Сложив эти объемы, мы получим более точное значение объема осадков, чем в прежнем случае, предполагавшим одинаковое среднее количество осадков по всей территории. Поскольку оба этих метода исходят из того, что наши объемы ограничены вертикальными стенками, вычисление объема очень просто как в растровой, так и в векторной модели. Для каждого слоя нарезки мы просто перемножаем значения площади и глубины. Вы можете сами попробовать это на простой БД в своей ГИС. Конечно, желательно иметь возможность определять объем как можно точнее. И увеличив число слоев нарезки, вы можете значительно улучшить точность расчета. Теоретически, можно уменьшать толщину слоев до бесконечности, что и делается в интегральном исчислении. К счастью, нам не нужно самим этим заниматься, так как эти алгоритмы уже встроены в программное обеспечение. Помните, что расчеты объема холма и объема озера по сути одинаковы в том, что одна из ограничивающих поверхностей является плоской. Конечно, это несколько упрощает задачу. Но если вы собираетесь определить объем рудной залежи, то вам придется иметь дело с двумя неровными поверхностями, причем обе - как правило - интерполированы. Тем не менее, вы можете использовать тот же подход, за тем исключением, что теперь вам нужно вычесть значения высот нижней поверхности из соответствующих значений верхней. Объем этой разностной поверхности даст вам искомую величину*. Хотя идея вычисления объема проста, она не всегда реализуется в коммерческих ГИС. Другие же программы специализируются на вычислениях такого рода (обычно, связанные с геологией и горным делом). Как и для других вычислений, здесь вы можете использовать экспорт/импорт данных при отсутствии нужных функций в основной программе. ДРУГИЕ ВИДЫ АНАЛИЗА ПОВЕРХНОСТЕЙ Помимо рассматривавшихся ранее операций существует множество других способов отображения и использования дополнительных покрытий с использованием данных о поверхности. Например, большинство ГИС позволяют отображать дополнительные покрытия наложенными на трехмерный вид поверхности. Эта возможность позволяет показать отношения между высотой и почвами, растительностью или распределением типов землепользования. Большинство программ также могут создавать покрытия из площади поверхности, занимаемой объемными объектами, такими как холмы. Вы также можете найти полезным определение реальной длины дороги, а не ее длины в плоскости, поскольку будет учтена топографическая поверхность. * В общем случае надо использовать модуль разности высот, так как поверхности могут пересекаться, что приведет к отрицательным разностям в некоторых точках и вычитанию соответствующих частичных объемов вместо их прибавления. — прим. перев. Последний метод особенно ценен для дорожно-строительных компаний, работа которых оплачивается по километражу дороги: при определении длины дороги по карте можно недосчитаться некоторой части расстояния и получить недостаточно средств для строительства. Обо всех этих возможностях программ следует справляться в документации, учитывая наличие возможности создания при помощи этих процедур покрытий, которые могут подвергаться дальнейшему анализу вместо простого отображения результатов, по которым нужно сходу принимать решение. ДИСКРЕТНЫЕ ПОВЕРХНОСТИ Как было сказано в начале главы, статистические поверхности могут представляться четырьмя различными способами. Мы уже рассмотрели основные методы представления непрерывных данных с использованием матриц высот, моделей TIN, изолиний. Но данные статистических поверхностей могут также встречаться как дискретные объекты. Для них мы должны рассмотреть некоторые дополнительные методы, как отображения, так и анализа. Карты плотности точек Этот подход чаще всего использует конкретные области, в которых подсчитываются объекты (число птиц на округ, тонн собранного зерна на ферму и т.д.). Другая распространенная форма карт плотности точек не использует отобранные области, а обозначает каждый объект одной точкой. Карты учета растений и животных, помещаемые в исследовательских статьях и книгах, или изыскания, проводимые многими службами биологических наблюдений, являются типичными представителями этого подхода. Когда точка указывает на более чем одно наблюдение, должны быть заданы три взаимосвязанных вопроса [Robinson et al., 1995]: сколько объектов представляется одной точкой, каков размер точки в связи с единицей дискретности, и где мы расположим точки после ответа на первые два вопроса. В то время как эти вопросы важны для картографического представления, их важность не проявляется, пока нам не придется вводить такие карты в ГИС. Чаще всего, когда нам приходится это делать, точки подсчитываются в каждом полигоне и преобразуются в одно значение. Затем они могут представляться посредством картограмм. Позднее мы рассмотрим эти карты подробнее. Кроме того, точки могут рассматриваться как непрерывные данные, и в таком случае мы можем выбрать центроид или центр тяжести для представления значения каждой области в виде одной точки, а затем выполнять операции над всем набором с помощью изолиний. Таким образом мы можем работать подобно тому, как это делалось с непрерывными данными, применяя интерполяцию или другие методы аппроксимации, анализ уклона и экспозиции и т.д. Когда каждая точка показывает некоторое количество объектов, скажем, местоположений гнезд птиц, мы должны полагать, что положения точек точны, и только их размер должен нас беспокоить при вводе подсчитанных объектов в ГИС. Однако, мы видим, что подавляющее большинство точечных карт, особенно те, что были созданы до появления современных технологий GPS и телеметрии, отображают точки в широком диапазоне размеров. Обычное дело - увидеть карты масштаба 1:100 ООО с точками, которые покрывают сотни и даже тысячи метров на земле. Покуда мы не имеем точных координат, мы вынуждены считать, что координаты точек наиболее верно отражаются их центрами. Хотя это и может быть не совсем правильно, у нас нет альтернатив. В некоторых случаях представляют интерес расстояния и группировки отдельных точечных распределений. Большинство ГИС не очень-то приспособлены для выполнения такого анализа, но это мы рассмотрим уже в следующей главе. Иногда мы также обнаруживаем, что каждая точка сопровождается дополнительными данными, записанными в любой из четырех шкал измерения. Но в контексте статистической поверхности мы обращаем внимание только нате, которые представлены в числовых шкалах. Если мы можем принять, что имеется непрерывность для таких величин, как массы птиц или размеры стай млекопитающих, представленные отдельными точками, то сможем выполнять операции с этими точечными данными, как если бы они были точечной выборкой топографической поверхности, особенно если они записаны в шкале интервалов или отношений. Всё же, предположение непрерывности в большинстве из этих случаев неверно, и нам придется рассматривать и сравнивать эти дискретные события по отдельности, либо статистически, либо через сравнения их пространственных отношений. Этот тип анализа мы рассмотрим опять же в следующей главе. Мы также упоминали о преобразовании карт распределения отдельных точек в некоторую форму площадного распределения (Глава 3), особенно в связи с зоокартографией. Как мы заметили, не существует точных инструкций о том, как выполнять эти преобразования, а простые графические методы, которые не связаны с функциями животных или других объектов в их окружении, могут давать ошибочные результаты. Чаще всего, если вас просят выполнить анализ таких распределений, вам нужно знать как можно больше о природе явления, либо из ваших собственных исследований, либо в результате подробных консультаций с вашими заказчиками. Карты хороплет Довольно часто статистические данные записываются для конкретных областей без учета конкретных местоположений. Мы видели, что можем считать такие данные непрерывными и оперировать с ними как с картами изолиний. Хотя это хорошо работает для распределений по большим поверхностям, чаще всего данные собираются для поиска максимумов и минимумов для каждой единичной области или для сравнения единичных областей с другими единицами других покрытий (более подробно в Главе 12). В Главе 3 мы рассматривали идею картограмм (value-by-area mapping), которые мы назвали также картами хороплет. И мы видели, как такие карты могут делаться с использованием выбранных классов или неклассифицированных данных в методе бесклассного картографирования хороплет (classless choropleth mapping). В среде ГИС, где можно создавать широкий спектр выходных карт, нам, скорее всего, нужно иметь исходные данные для каждой области, над которыми и выполняются все эти разнообразные функции ГИС. Здесь, однако, нам нужно пересмотреть классифицированные карты хороплет (classed choropleth map) вследствие той частоты, с которой нам приходится вводить такие карты для последующего анализа. Традиционные классифицированные карты хороплет, основанные на парадигме сообщения, хотя и могут быть введены в ГИС, мало полезны в этом контексте из-за методов их разработки. Обычно для определения того, как полигональные категории помещаются на карту, требуются три параметра: размер и форма областей, количество классов и метод определения границы класса. Как вы могли догадаться, чем больше размеры областей картограммы, тем больше данные обобщаются. Так, например, карта провинций и территорий Канады с лишь двумя классами создаст очень обобщенный набор данных, возможно, мало пригодный для дальнейшего анализа средствами ГИС. И наоборот, если бы показывались отдельные округа, и было бы 15 категорий группировки, мы имели бы больше полезной информации, которая с успехом могла бы быть введена в ГИС для анализа. Традиционные картографы стремятся сохранять формы областей похожими насколько это возможно, но эта практика приводит к модификациям данных, оказывающим влияние на наши возможности их анализа. Кроме того, к статистическим данным могут применяться многие методы численной классификации. Они включают последовательности равных интервалов, систематические неравные классовые интервалы и нерегулярные интервалы. Знание использованного подхода даст вам представление о том, как данные организованы, что может оказаться полезным в последующем анализе. Чаще всего, однако, классифицированные карты хороплет плохо подходят для анализа в ГИС, если только мы не получим больше информации связи областей с другими показателями - метод, называемый дасиметрическим картографированием. Дасиметрическое картографирование Для улучшения качества карт хороплет для использования в ГИС иногда применяется методика, называемая дасиметрическим картографированием. Поскольку карты хороплет, как классифицированные, так и бесклассные, отражают структуру областей сбора данных, они часто плохо показывают сами распределения. Дасиметрическое картографирование пытается разрушить эту искусственную структуру, чтобы выявить скрытые распределения. Вместо привязки к искусственным (нормативным) единицам сбора данных эти карты отображают области относительной однородности статистических данных [Robinson et al., 1995]. Они используют те же данные, но соотносят этот материал с другими сопровождающими данными или информацией из иных источников. Эти сравнения позволяют улучшить качество исходных карт хороплет за счет удаления границ областей первичного сбора данных. Но так как эта работа требует использования вспомогательной информации, мы отложим подробное обсуждение этой очень полезной методики до Главы 12, где будем сравнивать разные покрытия. В ГИС дасиметрическое картографирование чаще всего выполняется в процессе картографического наложения данных из других покрытий, нежели простым добавлением данных к исходной карте. Вопросы
6. Каково различие между регулярной и нерегулярной сетками с точки зрения выборки данных о поверхности? Каковы преимущества и недостатки каждой?
11. Опишите и схематически изобразите использование методов нелинейной интерполяции со взвешиванием. Почему в них иногда включаются барьеры?
17. О каких четырех моментах нужно помнить в любой процедуре интерполяции? Опишите проблему размещения выборки в изоплетном картировании. Что такое проблема седловой точки? Как она может быть решена?
20. Опишите метод ординат для определения объема поверхностного объекта. Объясните, как это делается в растровых и векторных ГИС.
|
