Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
Глава 10 Статистические поверхности Наши цифровые открытия продолжаются, теперь уже с новым пониманием того, что мы можем наблюдать. До сих пор мы концентрировались на точечных, линейных, и площадных объектах, но мы делали частые ссылки также и на поверхностные объекты. Мы видели, как последние могут быть смоделированы в компьютерной среде, и мы только что обнаружили, что они могут использоваться для изменения наших идей о том, что такое окрестность и как она работает. Поверхности часто используются для моделирования импеданса. Они могут представлять уклоны и экспозиции, а также области видимости и конкретные объекты наподобие долин, холмов и водоразделов. Но поверхности, с которыми мы столкнемся, не всегда будут топографическими. Как мы увидим, наш географический фильтр сможет различать поверхности, которые являются непрерывными или дискретными, гладкими или неровными, природными или антропогенными. Другими словами, наше определение поверхностей расширится, чтобы включить данные любого типа, которые либо существуют, либо могут подразумеваться существующими как изменяющиеся величины по всей области. Конечно, топографическая поверхность понимается легко, и в этой главе мы часто будем встречать рельеф местности в качестве классического типа поверхности. Поскольку значения высот существуют для каждой точки Земли, мы говорим, что такая поверхность непрерывна. Однако, когда мы пытаемся записать эту информацию, имея в виду создание обоснованных и количественно определимых описаний, мы обнаруживаем проблему, аналогичную попытке описать все деревья в лесу или все травинки на лугу, - данных так много, что мы просто не можем записать полный набор. Поэтому, как и прежде, мы должны произвести осмысленный отбор значений высоты, из которых мы смогли бы реконструировать топографию с заданной точностью. Имеется большое сходство между топографическими поверхностями и распределениями атмосферного давления, температуры и влажности - это непрерывные поверхности. Их значения также непрерывно распределены, но мы не можем регистрировать их в каждой точке. Вместо этого мы выбираем отдельные точки для представления всего распределения. Мы познакомимся с тем, как это делается, чтобы гарантировать адекватную запись наших наблюдений. В то время как даже непрерывные поверхности представляют определенные проблемы для исследователя, многие другие объекты не распределены непрерывно по всей области исследования; наоборот - они встречаются как дискретные объекты в определенных местоположениях. Но поскольку они встречаются очень часто, или потому что мы хотим регистрировать их на очень большой площади, эти дискретные данные также должны подвергаться частичной выборке. В одних случаях, как с непрерывными данными, мы будем делать отборы в определенных точечных местоположениях; в других мы должны собирать данные на всю площадь сразу. Например, путешествуя по Соединенным Штатам, мы наверняка обнаружили бы разницу в плотности населения в каждом округе. Вместо того чтобы тратить время на объезд всех округов и регистрацию отдельных людей на каждой остановке, мы просто берем число людей для каждого из примерно 3000 округов и используем их в качестве точечных замеров. В обоих случаях мы можем создать карты, которые напоминают изолинии топографической карты, исходя из предположения, что данные присутствуют повсюду. Таким образом, мы можем создать либо карту изолиний или блок-диаграмму, которая показывает форму распределения. И хотя мы знаем, что наши объекты не являются непрерывными, эти методы можно применять ради простоты представления картины распределения. Кроме того, мы увидим, как эти методы могут использоваться для предсказания значений распределений в местах, в которых мы не делали замеров. Время от времени мы будем фиксировать положения отдельных точечных объектов без указания каких-либо числовых атрибутов, так как эти данные представляют только местоположения точек; как следствие, мы не можем представлять их в форме карты изолиний или блок-диаграммы (тем не менее, существуют способы создания регионов на основе этих точечных паттернов, и мы увидим, почему такой выбор делается, и как это реализуется в ГИС.) Независимо от того, являются ли наши данные, представленные поверхностями, дискретными или непрерывными, их важность трудно переоценить. Первые ГИС создавались на основе моделей данных, разработанных для явлений, связанных с поверхностями (как, например, моделирование загрязнений). Современное специализированное программное обеспечение, часто связанное с ГИС, разрабатывалось для выполнения разнообразных операций представления данных, моделирования поверхностей, расчета объемов на основе поверхностей. Сейчас имеются огромные объемы поверхностных данных в форме, совместимой с ГИС, особенно связанные с рельефом и климатом. Со временем объем поверхностных данных будет расти со все большей скоростью по мере того, как будет все более очевидной важность анализа поверхностей. Вследствие высокой важности и доступности поверхностных данных важно рассмотреть данную тему в отдельности, несмотря на ее включение в предыдущие главы. Мы изучим виды данных, которые могут быть использованы в поверхностном моделировании, различные модели поверхностей, которые могут применяться для их отображения, узнаем, как предсказывать отсутствующие данные поверхности и как эти результаты могут использоваться в принятии решений. Мы также рассмотрим некоторые распространенные типы данных, представленных поверхностями, узнаем, как они были созданы, как мы можем использовать их в своей работе, как их можно преобразовывать в модели данных различных типов. И мы увидим, как можно создавать поверхностные данные по точечным наблюдениям разнообразных природных и антропогенных феноменов, чтобы поднять их ценность для моделирования. Если ваш интерес в ГИС связан с моделированием, планированием, принятием решений или просто разработкой баз данных, вам необходимо знакомство с данными и методами для создания, изменения и моделирования поверхностей. Если ваш интерес к этим данным обусловлен использованием их в собственной работе, применимость этой главы, возможно, более очевидна, чем для тех, кто будет работать над созданием баз данных для других. Для второй группы важно понимание того, когда и почему данные должны представляться в этом формате. ЧТО ТАКОЕ ПОВЕРХНОСТЬ? Поверхности - это объекты, которые чаще всего представляются значениями высоты Z, распределенными по области, определенной координатами Х и У. Параметр Z чаще всего ассоциируется с высотой рельефа местности, но не обязательно. На самом деле, любые измеримые величины, которые могут встречаться на определенной территории, могут рассматриваться как образующие поверхность. Обычно используется термин "статистическая поверхность" (statistical surface), поскольку значения параметра Z часто можно трактовать как статистическое представление величины рассматриваемых явлений или объектов [Robinson et al., 1995]. Возможно потому, что статистические поверхности расширяют наш географический фильтр включением таких параметров, как плотность населения, доход, плотность животных, атмосферное давление, они рассматриваются как одни из наиболее важных картографических концепций. За статистическими поверхностями стоит идея о том, что z-величина либо непрерывна по интересующей нас области, либо может считаться непрерывной в целях моделирования и картографирования. Статистические поверхности, образованные величиной, определенной во всех точках изучаемой области, называются непрерывными (continuous) (см. Рисунок 2.3). Те же, что встречаются только индивидуально, но с некоторым различием в числе на единицу площади (такие, как число домов на квадратный километр в каждой окрестности), называются дискретными (discrete) (см. Рисунок 2.3). Понимание статистических поверхностей этих двух типов может оказаться сложным, поэтому мы рассмотрим их по отдельности. Говорят, что непрерывные данные присутствуют в каждой возможной точке области. То, есть, существует возможность получения отсчета этой величины на сколь угодно малой площади где угодно в рассматриваемой области. Мы знаем, например, что температура имеется повсюду. Мы можем измерить ее в любой точке. Если мы это сделаем, то увидим, что она постепенно меняется от точки к точке непрерывной последовательностью. В некоторых случаях эти изменения невелики, возможно, менее чем на одну десятую градуса через 100 метров. Мы говорим, что имеем дело с гладкой поверхностью (smooth surface), с небольшим изменением статистической информации на единицу расстояния. Однако, в других случаях, например, когда мы пересекаем границу между двумя совершенно различными воздушными массами, значения температуры меняются очень резко. Такую поверхность мы называем неровной (rough), поскольку имеется резкое изменение статистических данных на небольшом расстоянии. Определение статистической поверхности как непрерывной означает, что имеется бесконечное количество точек, в каждой из которых может быть свое значение. Однако, провести измерения в бесконечном числе точек -физически невозможно, также как невозможно хранить бесконечный объем данных. Поэтому определение непрерывной поверхности с помощью бесконечного числа точек должно быть заменено моделью, которая использует существенно важные отсчеты (samples) рассматриваемой величины. Эти отсчеты представляют наиболее важные изменения поверхности как упрощенное представление. Изображение поверхностей на картах Статистические поверхности могут представляться посредством плотности точек, хороплет, дасиметрии и изолиний. Первые три чаще всего имеют дело с дискретными поверхностями, и мы их пока отложим. Четвертый метод наиболее часто используется для непрерывных данных, хотя он может использоваться и для дискретных данных, если принять, что  они являются непрерывными. Мы можем представить его себе как последовательность линий, окружающих нашу топографическую поверхность. Каждая линия, обычно называемая горизонталью в топографическом контексте, представляет все точки, имеющие одну и ту же высоту. Общее название линий, соединяющих точки одинаковых значений статистической величины, - изолиния. Рисунок 10.1 показывает перспективный вид топографического объекта с начерченными на нем горизонталями (изогипсами). При взгляде сверху изолинии выглядят как последовательность непересекающихся линий. Если они представляют топографический объект, такой как холм, то они замкнуты и очерчивают объект; если нет, то продолжаются до краев карты. То, что мы видим, есть линейные символы для отображения поверхностных данных. Более того, они позволяют нам наблюдать конкретные формы рельефа местности. Например, горизонтали, пересекающие речные долины, обычно выглядят как буква V, указывающая вверх по течению; на крутых склонах горизонтали расположены более плотно по сравнению с пологими склонами. Мы говорили прежде о классификации на основе уклона. Теперь вы видите, как для представления уклона могут применяться традиционные горизонтали (Рисунок 10.2). Мы можем обнаружить другой важный аспект изолиний, посмотрев еще раз на Рисунок 10.1. Расстояние по вертикали междулюбыми горизонталями одинаково, и это не случайно. 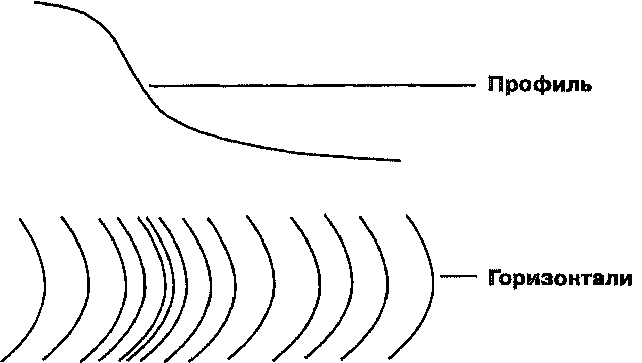 Рисунок 10.2. Расстояние между горизонталями и конфигурация поверхности. Более крутой уклон показывается более часто следующими горизонталями. Расстояние по вертикали выбирается таким, чтобы читающему карту было легче понимать, что эти линии представляют. Каждая карта имеет собственное вертикальное расстояние между горизонталями, в зависимости от быстроты изменения высоты. Эта установленная величина, называемая интервалом между изолиниями (contour interval), используется для деления (или квантования) изменения Z-величины на равные интервалы высот. Если бы мы использовали разные интервалы между соседними горизонталями, то не смогли бы интерпретировать частоту их следования как показатель уклона. ВЫБОРКА СТАТИСТИЧЕСКИХ ПОВЕРХНОСТЕЙ Существуют два основных метода получения Z-значений поверхности. Первый использует отобранные точки, и в этом случае карта изолиний называется изометрической (isometric). Этот метод наиболее часто применяется к построению горизонталей. Он также используется при создании карт атмосферного давления, температуры и других, получаемых на основе данных метеостанций, расположенных в определенных точках по всему земному шару. Но мы можем также работать и с данными, представляющими не точки, а небольшие области. Вспомним пример с численностью населения округов США. Хотя мы знаем, что эти данные -дискретные, при желании мы можем обращаться с ними как с непрерывными. Так что, предположив, что каждый из этих округов является точкой, мы можем создать карту изолиний такого же типа, как и в случае измерения параметра в отдельных точках. Этот тип карт, называемых картами изоплет (isoplethic map), требует от нас определения положений этих точек. Центроиды, которые могут использоваться в качестве таких точек, мы уже рассматривали*. В случае изоплетных карт существуют два подхода к выбору точек измерений. Первый называется регулярной сеткой (regular lattice, regular grid), так как точки расположены в узлах решетки, образованной прямыми линиями (Рисунок 10.3а). Регулярная сетка имеет преимущество простоты, когда не требуется задумываться о выборе точек измерения. Правда, существует некоторая сложность в выборе интервала между точками, так как поверхности могут быть как сильно пересеченными, так и сравнительно гладкими. В первом случае говорят о большем количестве информации на единицу площади, поскольку каждое изменение высоты является потенциальным элементом информации о форме поверхности. С увеличением плотности поверхностной информации требуется и большая плотность точек измерений. А это ведет нас ко второму методу отбора точек, основанному на нерегулярной сетке (irregular lattice) (Рисунок 10.3b). * Здесь нужно уточнение. Изаритмами называются "истинные" изолинии (они же -изометрические линии), т.е. линии равных значений непрерывной статистической величины. Существуют также изоплеты - линии равных значений дискретной статистической величины, они называются также псевдоизолиниями, так как между ними статистическая величина может изменяться скачком или быть неопределена. Внешне те и другие выглядят одинаково, но суть их различна. Изоплетами обычно изображаются вычисляемые, а не измерямые непосредственно величины, см.: Салищев К.А. Картоведение. М.; Изд-во МГУ, 1990. - прим. перев. В случае нерегулярной сетки мы определяем плотность точек на основе априорного представления о гладкости поверхности. Здесь мы не фиксируем плотность точек ни по горизонтали, ни по вертикали. Нет ограничения и по количеству точек в любой заданной области. Хотя может показаться, что отсутствие ограничений приведет к росту числа точек измерений, на самом деле это не обязательно так. 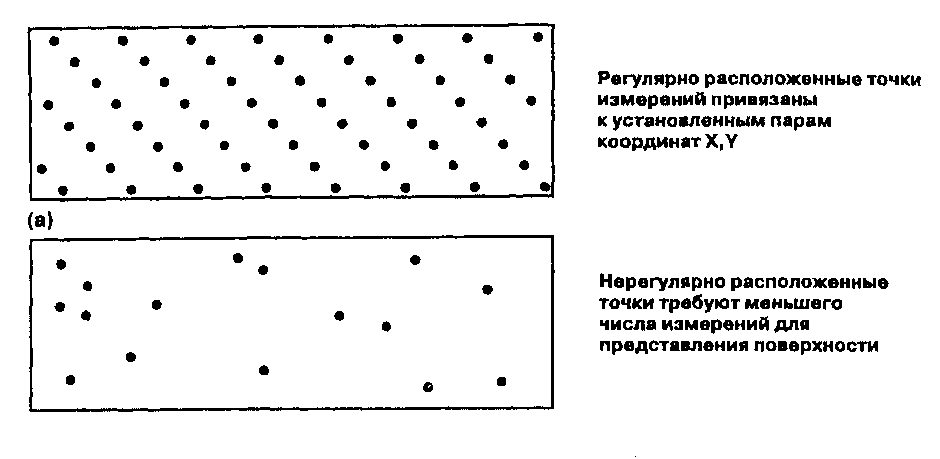 (b) Рисунок 10.3. Регулярная (а) и нерегулярная (b) сетки. Точки могут быть как самими местами измерений, так и представителями данных в БД ГИС. Мы можем получить хорошую модель поверхности при меньшем числе точек, уменьшая их плотность на относительно гладких участках по сравнению с тем, что требовалось бы при использовании регулярной сетки. Более высокая плотность точек на таких участках не дает по существу новой информации, а только приводит к ненужному расходу времени и сил на сбор данных, а также места для их хранения. ЦИФРОВЫЕ МОДЕЛИ РЕЛЬЕФА Определив процедуры выбора точек измерений, нам нужно понять, как поверхность может быть представлена внутри компьютера, как в растровых, так и в векторных системах. Мы уже имели дело с моделью нерегулярной триангуляционной сети (TIN), однако она является лишь одним из способов представления Z-величин в компьютере, вместе образующих группу "цифровых моделей рельефа" (ЦМР) (digital elevation models (DEMs)). Это могут быть математические модели (mathematical models) или наглядные, визуальные модели (image models)* (включая TIN), разработанные для обработки полевых данных или представления на бумажной карте [Mark, 1978]. Хотя математические модели весьма полезны, большинство * по-видимому, автор имеет ввиду амалитическое (формулой) и наглядное (как набор точек) представление поверхностей - прим. перев. Глава 10 имеющихся сегодня ЦМР являются моделями изображения, поэтому мы сфокусируемся именно на них. Модели изображения бывают двух типов: основанные на точках и основанные на линиях. Модели изображения на основе линий - почти что графический эквивалент традиционного метода карт изолиний. Во многих случаях такие модели создаются сканированием или оцифровкой существующих изолиний. Целью является извлечение формы поверхности из имеющихся линий, которые ее представляют. После ввода эти данные представляются либо как линейные объекты, либо как полигоны с определенной высотой в качестве атрибута. Поскольку на такой модели данных неудобно определять уклон, экспозицию или создавать отмывку рельефа, обычно ее преобразуют в точечную модель. В результате получается то, что называют дискретной матрицей высот (discrete altitude matrix). Эта матрица соответствует методу точечного изображения поверхности, где каждая точка несет одно значение высоты. Это в чем-то похоже на точечную дискретизацию непрерывной поверхности. Подобно полевым методам съемки топографии, матрица высот использует множество точек, отобранных из стереопар или аэрофотоснимков, обычно с применением устройства под названием аналитический стереоплоттер (analytical stereo-plotter), который определяет значения высот по смещению между двумя изображениями [Kelly et al., 1977]. Также, как и в полевых измерениях, аналитик может использовать регулярную или нерегулярную сетку. Поскольку регулярная сетка приводит к избыточности данных на участках с минимумом топографической информации и недостатку данных на участках с большим объемом топографической информации, нерегулярная сетка более предпочтительна. Автоматические сканирующие стереоплоттеры [сами] повышают плотность выборки на участках быстро меняющейся топографии, что существенно упрощает дело [Markarovic, 1973]. * Точнее, есть некоторая степень фундаментальной неопределенности этих значений. Здесь есть и парадоксальный момент: с точки зрения теории информации добавление Нерегулярные сетки могут быть преобразованы в модель TIN двумя способами. Первый заключается в использовании самих точек сетки в качестве вершин треугольных граней TIN. Его достоинство — в отсутствии требования ввода дополнительных данных. Во втором подходе расстояния между точками и их значения высот используются при интерполяции (interpolation) значений вершин регулярной матрицы треугольных граней TIN. Интерполяция как аналитическая техника будет рассматриваться в следующей главе. Хотя в результате интерполяции повышается количество точек, представляющих данные матрицы высот, интерполированные значения не так точны, как измеренные*. Таким образом, любая модель, созданная с применением этой техники, имеет дополнительный объем погрешности по высоте. ЦМР легко могут быть получены для многих частей мира как матрицы высот с сетками 63.5 м, полученными с топографических карт масштаба 1:250'000; появляются и сетки с карт более крупного масштаба, таких как 1:25'000, и аэрофотоснимков (Приложение 1). Среди преимуществ ЦМР, полученных с помощью интерполяции с созданием регулярной матрицы, является легкость ввода в растровые ГИС. ЦМР, целиком основанные на нерегулярной сетке, при вводе в растровые ГИС должны будут подвергаться растровой интерполяции. Далее мы рассмотрим представление непрерывных поверхностей в растровых ГИС и процессы интерполяции. РАСТРОВЫЕ ПОВЕРХНОСТИ В растровой модели данных каждая ячейка может иметь только одно значение высоты. По сути, это приводит к тому, что непрерывная пространственная величина получает дискретное представление (Рисунок 10.4). Помимо того, что каждая ячейка растра имеет только одно значение высоты, она еще и занимает некоторую площадь, с увеличением которой снижается точность представления поверхности в растровой модели данных. Таким же важным, как и размер ячейки, является вопрос о том, где в ее пределах находится реальная точка присвоенной ячейке высоты. Вы можете указать это положение: центр ячейки или один из четырех ее углов (Рисунок 10.4). При анализе топографических поверхностей выбор этих точек будет иметь влияние на результаты вычислений. Например, при определении маршрутов наименьшей стоимости в Главе 8 мы начинали в центре каждой ячейки растра, так как считали, что значение высоты относилось именно к этой точке. Если бы ячейки были закодированы так, что значение высоты относилось к одному из четырех углов, то вычисленные расстояния были бы смещены по меньшей мере на половину ширины ячейки. Поэтому, прежде чем анализировать такие величины, как расстояния, уклон и экспозицию склона, вам следует уточнить, где ваша растровая ГИС на самом деле помещает значения высот. интерполированных точек снижает количество информации, приходящееся на каждую точку, так как сама интерполяция не увеличиваает количество информации. Если же мы используем интерполированные точки вместо измеренных, то должны также оценивать и достоверность интерполированных данных. — прим. перев. Во многих случаях данные будут доступны только для части узлов сетки, используете ли вы растровую или векторную модель. Скорее всего вы получите высотные данные как матрицу высот в одной из двух форм, которые мы обсуждали - регулярной или нерегулярной сетки. Если регулярная сетка достаточно мелка, чтобы соответствовать вашему размеру ячеек растра, то вы сможете легко преобразовать значения высоты в каждой вершине сетки непосредственно в значения высот ячеек растра (опять же, решив заранее, где будут расположены точки высот). Когда данные представлены в форме нерегулярной сетки, перед вами встанет необходимость оценивать или предсказывать все отсутствующие значения. Этот процесс, называемый интерполяцией, необходим, потому что все ячейки растра должны иметь значения высоты. Как мы увидим позже, интерполяция - полезный аналитический инструмент для моделирования, как сама по себе, так и при объединении с другими методами анализа для построения более сложных моделей. 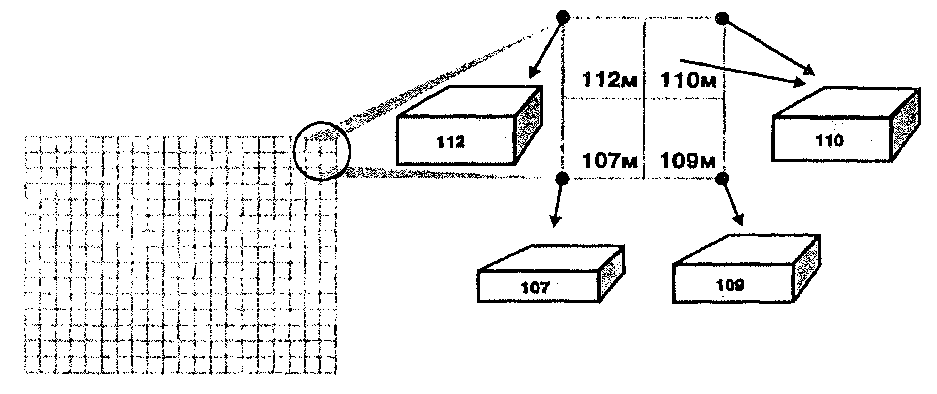 Рисунок 10.4. Дискретизация поверхности. Растровое представление непрерывной поверхности. Каждой ячейке присваивается определенное значение высоты. Чтобы обеспечить точный анализ в дальнейшем, важно решить, где именно в пределах ячейки находится точка с этой высотой. ИНТЕРПОЛЯЦИЯ Поскольку для непрерывных поверхностей, - топографических, экономических, демографических или климатических мы используем выборку, - нам нужна возможность изображать с приемлемой точностью наблюдаемые объекты. В традиционной картографии, например, точечные значения выборки высот или значений для других статистических поверхностей преобразуются в визуальную форму, использующую изолинии. Но нам нужна возможность создания и других форм визуального представления, таких как блок-диаграммы и карты отмывки рельефа. И, конечно, нам нужна возможность определения уклонов, экспозиций склонов и поперечных сечений и предсказания неизвестных значений высот для объектов, на которые у нас нет соответствующих данных. Интерполяция обеспечивает многое из того, что нужно для выполнения этих операций. Процесс интерполяции теоретически может быть очень прост, но он требует одно априорное утверждение. Вначале давайте рассмотрим математическую основу интерполяции на примере математических прогрессий. Прогрессии - это числа, которые расположены в определенном порядке. Последовательность 1 2345678 9 10 является линейной или арифметической прогрессией, так как каждая пара соседних чисел имеет постоянную разность (в данном случае 1). Другие примеры арифметических прогрессий: 10 20 30 40 50 60 70 80 90 100 (разность = 10) 1000 900 800 700 600 500 400 300 200 100 (разность = -100) Существует также разновидность прогрессий, где вместо сложения используется умножение, такая прогрессия называется геометрической. Линейная интерполяция Внутри этих простых последовательностей мы можем легко идентифицировать упомянутое выше априорное утверждение, а именно то, что каждое последующее число определяется простым математическим действием. Если мы можем распознать это действие, то сможем восстанавливать пропущенные значения. Так, например, если нам известно, что в последовательности {30, 40, 60, 70, 80, 100} пропущены два числа, то мы можем предположить, что эта последовательность является арифметической прогрессией и что между парами чисел {40, 60} и {80, 100} пропущены числа 50 (=40+ 10) и 90 (= 80 + 10). Это, по сути, и есть линейная интерполяция (linear interpolation), используемая для определения неизвестных значений высот между точками с известными значениями высоты. Возьмем простой пример, показанный на Рисунке 10.5. Здесь изображена последовательность точек со значениями высоты от 100 м до 150 м. Если мы предположим, что поверхность меняется линейным образом, как в арифметической прогрессии, то становится очевидным, что четыре числа на равных промежутках друг от друга могут быть проинтерполированы как 110, 120,130 и 140 метров высоты. Если мы сделаем это для всей поверхности, а не для одного сечения, то сможем получить значения для всех точек с интервалом по 10 метров. Соединив плавными линиями эти точки, мы сможем создать контуры для 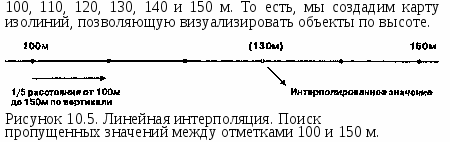 До сих пор мы имели дело с линейной интерполяцией, предполагая, что поверхность изменяется линейным образом. Однако, последовательность отсчетов высоты не всегда следует линейному закону. В некоторых случаях она скорее логарифмическая, в других может предсказываться только для небольших участков поверхности. В таких случаях линейная интерполяция не даст адекватных результатов. Кроме того, существуют и другие подходы к поверхностной информации, которые могут потребовать определения общего закона изменения поверхности, а не детального ее описания. Некоторые из этих методов могут быть весьма сложными математически, так что мы ограничимся концептуальным уровнем рассмотрения некоторых методов нелинейной интерполяции, чтобы понять, как их можно использовать в ГИС наилучшим образом. Другие методы интерполяции Здесь мы рассмотрим три метода интерполяции: метод обратных взвешенных расстояний (ОВР), метод поверхности тренда и кригинг. Есть книги, детально рассматривающие и многие другие методы [Burrough, 1983; Davis, 1986], здесь мы ограничимся только самыми известными. Метод ОВР исходит из предположения, что чем ближе друг к другу находятся точки данных, тем ближе их значения. Например, двигаясь по склону холма, вы можете отметить большее сходство в значениях высоты в близлежащих к вашему текущему положению точках по сравнению с точками, которые удалены гораздо дальше. То же можно было бы сказать, если бы вы двигались по равнине. Для более точного описания топографии нам нужно выбрать точки окрестности, которые демонстрируют это сходство поверхности. Это достигается несколькими приемами поиска, включая определение окрестности на заданном удалении от каждой точки, предварительным заданием числа точек выборки данных или выбором определенного числа точек в квадрантах или октантах (когда, например, для интерполяции используется одна точка из каждого квадранта) [Clarke, 1990]. 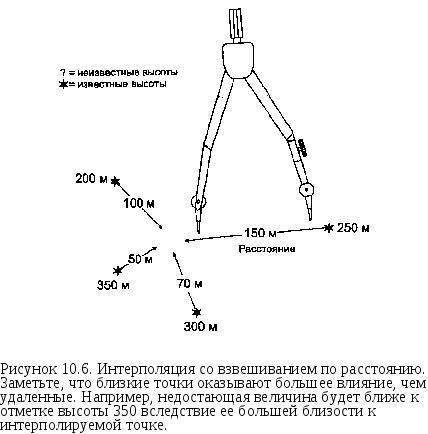 Какой бы метод ни использовался, компьютер должен измерять расстояние между каждой парой точек и от каждой начальной точки. Затем значение высоты в каждой точке взвешивается в зависимости от квадрата расстояния, так что более близкие точки вносят больший вклад в определение интерполируемой высоты по сравнению с более удаленными (Рисунок 10.6). Существуют многие модификации этого подхода. Одни методы сокращают объем вычислений применением "поиска с обучением" [Hodgson, 1989], другие используют в качестве весового коэффициента вместо второй степени третью или более высокую, третьи учитывают барьеры, представляющие береговую линию, скалы или иные непреодолимые объекты, которые могут воздействовать на результаты интерполяции [Shepard, 1968]. Как и при использовании барьеров в других задачах моделирования, процесс интерполяции не может распространяться через барьер. В некоторых случаях нас больше интересует общие тенденции поверхности, нежели точное моделирование мелких неровностей. Например, нас может интересовать общее распределение населения по стране для демографического исследования, или подход к каменноугольному пласту с поверхности, чтобы определить, сколько необходимо удалить поверхностного грунта. Наиболее распространенный подход к такой характеристике поверхности называется поверхностью тренда. Как и в методе ОВР, для поверхностей тренда мы используем наборы точек в пределах заданной окрестности, которая строится на основе любого из способов, перечисленным для методов со взвешиванием. В пределах каждой окрестности строится поверхность наилучшего приближения на основе математических уравнений, таких как полиномы или сплайны (polynomials, splines). Эти уравнения являются нелинейными зависимостями, которые аппроксимируют кривые или другие формы числовых последовательностей. Чтобы построить поверхность тренда, каждое из значений в окрестности подставляется в уравнение. Из уравнения, использованного для построения поверхности наилучшего приближения, получается одно значение и присваивается интерполируемой точке. Процесс продолжается для других целевых точек; кроме того, поверхность тренда может быть расширена на все покрытие. Число, присваиваемое целевой ячейке, может быть простым средним всех значений поверхности в окрестности, или оно может быть взвешенным с учетом определенного направления, в котором ориентирован тренд. Поверхности тренда, как мы видели в Главе 9, могут быть плоскими, показывая общую тенденцию для всего покрытия, или они могут быть более сложными. Тип используемого уравнения (или степень полинома) определяет величину волнистости поверхности. Чем проще выглядит поверхность тренда, тем меньший порядок, как говорят, она имеет. Например, поверхность тренда первого порядка будет выглядеть как плоскость, простирающаяся под некоторым углом по всему покрытию, т.е. она имеет тенденцию в одном направлении. Если поверхность имеет один изгиб, то такую поверхность называют поверхностью тренда второго порядка (Рисунок 10.7), и т.д. Последний рассматриваемый метод интерполяции, кригинг (kriging), оптимизирует процедуру интерполяции на основе статистической природы поверхности [Oliver and Oliver, 1990]. Кригинг использует идею регионализированной переменной (regionalized variable) [Blais and Carlier, 1967; Matheron, 1967], которая изменяется от места к месту с некоторой видимой непрерывностью, но не может моделироваться только одним математическим уравнением. Оказывается, многие топографические поверхности подходят под это описание, также как и поверхности изменения качества руды, вариации качества почв и даже некоторые показатели растительности.  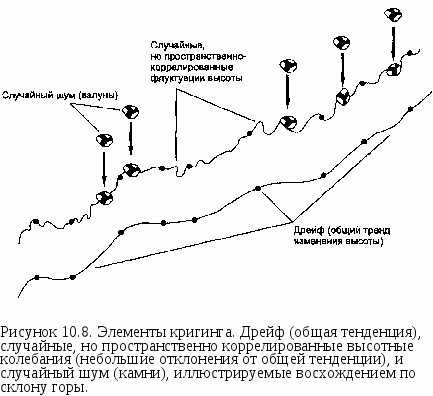 Рисунок 10.7. Порядки поверхностей тренда. Поверхности первого, второго и третьего порядка в зависимости от сложности полинома, используемого для представления поверхности. Кригинг обрабатывает эти поверхности так, считая их образованными из трех независимых величин. Первая, называемая дрейфом или структурой (drift or structure) поверхности, представляет поверхность как общий тренд в определенном направлении. Далее, кригинг предполагает, что имеются небольшие отклонения от этой общей тенденции, вроде маленьких пиков и впадин, которые являются случайными, но все же связанными друг с другом пространственно (мы говорим, что они пространственно коррелированны). Наконец, мы имеем случайный шум (random noise), который не связан с общей тенденцией и не имеет пространственной автокорреляции. Кларк [Clarke, 1990] удачно иллюстрирует этот набор значений посредством аналогии: когда мы идем вверх по горе, рельеф местности изменяется в восходящем направлении между отправной точкой и вершиной; это - дрейф. По пути мы встречаем локальные снижения и повышения, сопровождаемые случайными, но коррелированными высотами. Также по пути нам встречаются камни, которые приходится переступать, их можно представлять как шум значения высоты, так как они не связаны непосредственно с основной поверхностной структурой, прежде всего создающей изменения высоты (Рисунок 10.8). С каждой из трех переменных надо оперировать в отдельности. Дрейф оценивается с использованием математического уравнения, которое наиболее близко представляет общее изменение поверхности, во многом подобно поверхности тренда. Ожидаемое значение высоты измеряется с использованием вариограммы (variogram, semivariogram) (Рисунок 10.9), на которой по горизонтальной оси откладывается расстояние между отсчетами, называемое лагом (lag), вертикальная ось несет так называемую полудисперсию (semivariance), которая определяется как половина дисперсии (квадрата стандартного отклонения) между каждым значением высоты и его соседями. Таким образом, полудисперсия является мерой взаимосвязи значений высоты, зависящей от того, как близко друг к другу они находятся. Затем через точки данных проводится кривая наилучшего приближения, давая нам меру пространственно-коррелированной случайной компоненты. Посмотрев внимательно на график полудисперсии, вы можете заметить, что когда расстояние между точками отсчета высоты мало, полудисперсия тоже мала. Это значит, что значения высоты близки и, следовательно, взаимосвязаны вследствие их пространственной близости. С ростом расстояния между точками растет и полудисперсия, показывая быстрый спад пространственной корреляции значений. Наконец достигается критическое значение лага, известное как предельный радиус корреляции (range), при котором дисперсия достигает предела и в дальнейшем остается постоянной. Чем ближе друг к другу находятся отсчеты внутри диапазона роста (т.е. от нуля до точки прекращения роста кривой на графике), тем более похожими они должны быть. За пределами радиуса корреляции расстояние между точками не имеет значения, они совершенно независимы на любом удалении, превышающем радиус. Это говорит нам о том, какая окрестность должна быть использована (например, в ОВР-интерполяции), чтобы охватить все точки, значения высоты которых будут взаимосвязаны. 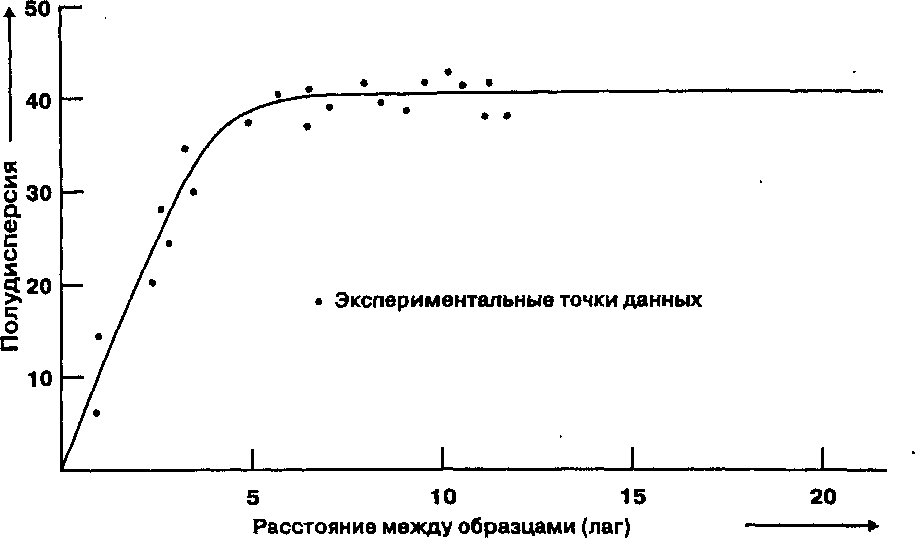 Рисунок 10.9. Пример вариограммы. Она показывает связь между точками данных и аппроксимирующей линией. Обратите внимание, что в некотором диапазоне значений лага высоты связаны друг с другом (дисперсия высот связана с лагом), а вне его нет вообще никакой связи (дисперсия достигает максимального значения), так как точки находятся слишком далеко друг от друга. Третьим по важности моментом графика является то, что аппроксимирующая кривая не проходит через начало координат. По идее, если между отсчетами нет расстояния, то не должно быть и дисперсии, так как отсчеты являются по сути одной точкой. Но нужно помнить, что кривая является оценочной. Разница между нулевой дисперсией при нулевом лаге и предсказываемым положительным значением является остаточной, пространственно некоррелированной "шумовой" дисперсией, которая называется остаточной дисперсией (nugget variance). Как указывает Бэрроу [Burrough, 1986], эта остаточная дисперсия "объединяет дисперсию ошибок измерения с пространственной дисперсией, которая имеет место на расстояниях, гораздо меньших, чем интервал взятия отсчетов, и которые в дальнейшем не могут быть устранены". Теперь, имея три составляющие регионализированной переменной, определенные вариограммой, мы можем определить веса, необходимые для выполнения интерполяции в локальных окрестностях. Однако, в отличие от ОВР, веса для интерполяции в пределах окрестностей выбираются с целью минимизации дисперсии оценки для всех комбинаций отсчетов высоты. Эта дисперсия может быть получена непосредственно из модели, по которой была прежде создана вариограмма. Кригинг существует в двух основных формах. Общий (universal) кригинг, чаще всего применяется, когда поверхность оценивается по нерегулярно распределенным отсчетам при наличии тренда (условие, называемое нестационарностью). Ординарный (ordinary) кригинг является элементарной формой и предполагает, что данные стационарны (не имеют тренда), изотропны и собраны через равные интервалы [Davis, 1986]. Наиболее часто локальный кригинг используется для поиска точечных оценок на основе других точечных данных, а не для определения поверхностей*. Кригинг часто дает довольно точные оценки пропущенных значений, но эта точность обходится ценой времени и вычислительных ресурсов. Но даже при этом кригинг имеет еще одно преимущество перед другими методами интерполяции, - он не только дает интерполированные значения, но также и оценку возможной ошибки этих значений. Это может навести на мысль, что данный метод следует применять повсеместно, но увы. Когда мы имеем дело с большим уровнем локального шума из-за ошибок измерений или большие вариации высоты между отсчетами, в данном методе становится трудным построение кривой полудисперсии. А в таких условиях результаты кригинга будут не лучше, чем полученные другими методами. * Здесь автор не точен. Ординарный кригинг по своей сути является лишь улучшением метода ОВР, в котором учитываются не только расстояния от интерполируемой точки до исходных, но и расстояния между самими исходными точками так, что веса более близких друг к другу исходных точек уменьшаются. Этот метод превосходит простой метод ОВР именно тогда, когда точки расположены с неравными интервалами, благодаря учету пространственной корреляции исходных данных. Разработан также вариант метода, уменьшающий объем вычислений в случае интерполяции многих точек при размещении исходных точек в узлах регулярной сетки, он называется блочным кригингом (block kriging). Метод позволяет также учитывать анизотропность, - в этом случае вариограмма аппроксимируется функцией двух независимых аргументов. — прим, перев. В векторных моделях данных (чаще всего TIN) процесс интерполяции проще всего выполняется выборкой точек с их значениями высоты и преобразованием их в точечную матрицу высот. И уже к этому точечному покрытию может быть применен один из описанных алгоритмов. В действительности, сама модель TIN может выполнять интерполяцию [McCullagh and Ross, 1980], но это мы оставим для более углубленного курса геоинформатики. В растровых покрытиях значения высоты обычно соотносятся с точками, расположенными внутри каждой ячейки (например, в центре). Для интерполяции мы можем использовать именно эти точки и действовать по одному из описанных выше методов. В этом случае интерполируемым ячейкам растра присваиваются значения высоты, полученные для представляющих их точек. Если ваша ГИС не содержит нужного алгоритма, то, как правило, вы можете преобразовать точечные покрытия в форму, понимаемую специализированным программным обеспечением, рассчитанным на работу с пространственными данными. Затем его выходные данные могут быть преобразованы обратно для дальнейшего анализа внутри ГИС. Существуют и другие обзоры методов интерполяции, к которым вы можете обратиться [Lam, 1983; Flowerdew and Green, 1992]. ПРИМЕНЕНИЕ ИНТЕРПОЛЯЦИИ Интерполяция полезна для создания изолиний, описывающих поверхности. Она может также использоваться для отображения поверхности средствами блок-диаграмм или карт с отмывкой рельефа. Но для чего еще может использоваться интерполяция? Допустим, что вы планируете жилую застройку и не хотите попасть в зону наводнений, но у вас нет карты, показывающей границы этой зоны. При этом вы знаете, что максимальный уровень наводнений за сто лет составил 60 метров над уровнем моря. У вас также имеются заметки о нескольких прежних участках строительства, и они включают данные высот для каждого построенного дома. Изобразив данные на карте местности, вы можете использовать интерполяцию для оценки высот вашего участка. По этим данным вы сможете начертить изолинию, показывающую зону наводнений за 100 лет, и, просто сравнив ваше местоположение с ней, узнаете, нужно ли менять место. Теперь предположим, что вы прокладываете шоссе по ненанесенной на карту территории и не можете начать строительство, не зная среднего градиента. Вы можете создать карту поверхности тренда, чтобы показать общий характер уклона. Или, положим, вы являетесь горным инженером, пытающимся определить общий тренд рудного месторождения на основе информации из множества кернов, показывающих вершину и дно залежи. Метод интерполяции поверхности тренда даст информацию о толщине рудного слоя и его уклона под землей. Кроме того, метод кригинга окажется полезным в оценке качества рудного слоя, так как рудные пласты хорошо описываются регионализованными переменными. На самом деле, существует множество применений интерполяции в различных областях. Если вы хотите предсказать изменения состава почвы вдоль наклонной поверхности, если исследуете тенденции в растительном покрытии на удалении от источника воды, или если вы интересуетесь тенденциями изменения численности населения на большой территории, исходя из выборочных данных за прошедшие десятилетия, то все эти виды анализа требуют какого-либо вида интерполяции. О чем вам следует помнить, так это о том, что интерполяция является, по сути, предсказательной моделью. ПРОБЛЕМЫ ИНТЕРПОЛЯЦИИ Мы рассмотрели несколько методов интерполяции, при выполнении которых должны учитываться следующие четыре фактора:
В общем случае можно сказать, что чем больше исходных точек мы имеем, тем более точной будет интерполяция и тем с большей вероятностью интерполированная поверхность будет хорошей моделью. Однако, существует предел числу отсчетов, которые могут быть сделаны для любой поверхности. Постепенно достигается момент снижения отдачи: большее количество точек не улучшает существенно качество результата, но лишь увеличивает время вычислений и объем данных. В некоторых случаях избыточные данные могут приводить к необычным результатам, поскольку группы точек в областях, где данные могут быть легко собраны, могут создать неравномерное представление поверхности, и, следовательно, неодинаковую точность. Другими словами, большее число точек не всегда улучшает точность: Рисунок 10.10 показывает, что при некотором количестве точек точность на самом деле снижается. 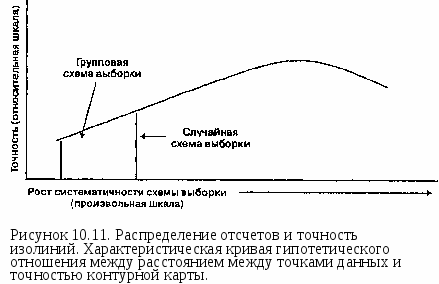 Конечно, количество исходных точек часто является функцией формы поверхности. Чем сложнее поверхность, тем больше точек данных требуется. А для важных объектов, таких как впадины и долины рек, требуются дополнительные точки данных, чтобы гарантировать представление необходимой подробности. Вдобавок, хотя положение точек измерения друг относительно друга имеет влияние на точность интерполяции, сама зависимость не является линейной (Рисунок 10.11). Проблема размещения отсчетов усугубляется, когда мы рассматриваем интерполяцию по данным, собираемым по областям, для создания карты изоплет. Мы знаем, что ГИС имеют возможность определения центроида каждого полигона или центра распределения каждого полигона. Когда точки данных распределены относительно равномерно, легче всего использовать метод центроида ячейки (centroid-of-cell). А метод центра тяжести наиболее полезен, когда точки выборки сгруппированы или неравномерно распределены. Однако, при обоих методах существует вероятность, что центр окажется вне полигона выборки, особенно если полигоны имеют необычную форму. Когда такое случается, наиболее легким решением обычно является "подтягивание" центроида или центра тяжести к наиболее близкой к нему точке полигона (что, вероятно, потребует вмешательства оператора). 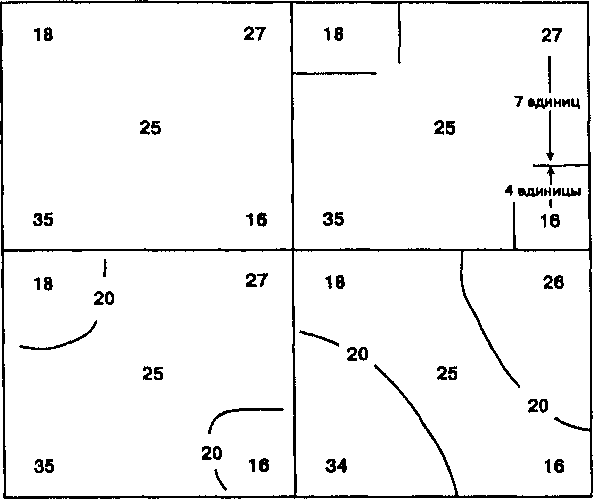 Рисунок 10.12. Проблема седловой точки. Проблема седловой точки с расположением точек в вершинах прямоугольника. Обратите внимание на два возможных решения одной задачи интерполяции. * Во-первых, прямоугольник-лишь частный (и простейший) случай для данной проблемы: Проблема седловой точки (saddle-point problem), называемая иногда проблемой альтернативного выбора, возникает тогда, когда две точки одной пары диагонально противоположных Z-значений, образующих прямоугольник, расположены ниже, а две точки другой диагональной пары находятся выше того значения, которое пытается найти алгоритм интерполяции (Рисунок 10.12а)*. Это обычно случается только при линейной интерполяции, но когда это происходит, программа встает перед лицом двух возможных решений одного вопроса: где провести изолинию (Рисунок 10.12). Простым способом решения этой проблемы является помещение среднего от двух, полученных по диагоналям, интерполированных значений в точке пересечения диагоналей (Рисунок 10.13). 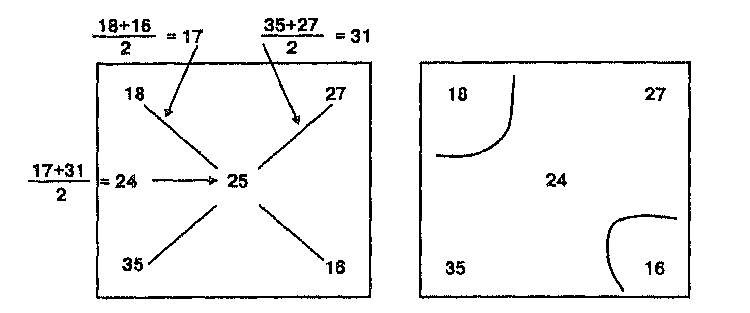 Рисунок 10.13. Решение проблемы седловой точки. Решение использует среднее значение, помещенное точно в центр. Последняя проблема, которая должна учитываться при интерполяции, является общей для операций в ГИС, имеющих дело с областью, в пределах которой собираются точки данных. А именно, чтобы интерполяция работала должным образом, интерполируемые точки должны быть окружены точками с известными значениями со всех сторон. Но если мы, как часто бывает, выбираем для анализа всю область исследования и используем ту же область для выполнения интерполяции, то вскоре нам приходится интерполировать точки вблизи границы области. И с приближением к границе алгоритм интерполяции вынужден использовать исходные точки только с трех и даже двух сторон от интерполируемой. Как мы видели, наилучшие результаты интерполяции достигаются тогда, когда мы можем расширять окрестность по всем направлениям для выбора исходных точек и определения весов. В отсутствие этих окружающих точек алгоритм будет использовать то, что есть, допуская систематическую ошибку вдоль границы. В качестве примера давайте попробуем выполнить интерполяцию вдоль левой границы карты. Условимся, что эта граница проходит по холму, который поднимается от центра карты к ее левой границе. Смежный лист карты показывает, что холм продолжает расти и за левой границей нашей очевидно, что здесь мог бы быть любой четырехугольник и даже многоугольник с большим числом вершин; можно также показать, что неоднозначность возникает и при других, не образующих столь явного седла, соотношениях значений исходных точек. Во-вторых, это скорее проблема правомерности использования того или другого метода интерполяции, каждый из которых может давать своё решение, в том числе и существенно отличающееся от приведенного. — прим. перев. |