Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
Глава 11 Пространственные распределения До сих пор наше путешествие фокусировалось на характеристиках наблюдаемых объектов. Но для правильной оценки окружения нам нужно знать также отношения между отдельными элементами, которые мы видим, и пространством между ними. Теперь мы будем рассматривать не объем пространства, занимаемый объектом, или его форму, а расположение объектов в пространстве, которое может характеризоваться количеством объектов в определенной области, тем, как они распределены - равномерно или группами. Мы рассмотрим отношения удаленности между самими объектами и их связь с общим размером занимаемой области. Распределения могут наблюдаться во многих ситуациях. Мы знаем, например, что некоторые распределения человеческого населения характеризуются большой разбросанностью, подобно фермам в сельской местности. Другие распределения населения больше сконцентрированы в то, что мы называем городами. Растения и животные могут быть распределены равномерно или тоже в более плотные группы. Даже природные объекты, такие как типы отложений и формы рельефа — реки и холмы, горы и долины, - могут встречаться как отдельно стоящие так и в больших группах. Антропогенные объекты, такие как дороги, ограждения, дома, также могут быть определенным образом расположены. По мере развития нашего географического фильтра мы будем видеть еще больше. Видение того, что существуют различия в пространственном расположении объектов, позволяет нам формулировать вопросы о том, каковы картины этих распределений, как они могут быть классифицированы, и что они могут поведать нам о процессах, их создавших. Если мы повторно посетим места, где впервые наблюдали расположение объектов, будь то в реальном мире или в мире ГИС, то мы увидим, что наблюдаемая картина изменилась. Регионы, которые прежде имели разрозненные распределения, теперь могут демонстрировать признаки группирования. Объекты, которые были когда-то организованы в пространстве случайным образом, теперь встречаются в регулярных, повторяющихся паттернах. Одни паттерны могут проявлять расширение и рост упорядоченности, другие - сжатие или деструктуризацию. Области могут сливаться, отдельные линейные объекты - соединяться в сети, установившиеся дюны — перемещаться и рассеиваться. Во всех этих случаях время является важной составляющей частью в нашем понимании расположения в пространстве. И вскоре мы задаёмся вопросом: что за процессы вызывают переход от одного распределения к другому? Мы можем задаваться вопросами: каковы могут быть направления изменений, существуют ли движущие силы, которые мы можем понять, каковы могут быть верхние и нижние пределы этих сил, и т.д. В данной главе мы будем заниматься главным образом распределениями объектов одного покрытия. Это, конечно, ограниченный подход, и по моему опыту я могу сказать, что вы вскоре сами увидите методы, в которых используются данные других покрытий. Немного терпения, и вы узнаете, как распределения объектов могут сравниваться друг с другом. А там уже недалеко и до сравнения объектов разных покрытий, что является темой Главы 12. ПРОСТРАНСТВЕННЫЕ РАСПРЕДЕЛЕНИЯ Пространственное распределение это расстановка, порядок, концентрация или рассеянность, соединенность или бессвязность многих объектов в пределах заключающего их географического пространства. До сих пор рассматриваемые нами методы имели дело главным образом с отдельными объектами или наборами объектов, когда они могли быть определены как регионы, окрестности или представлены как статистические поверхности. Мы лишь очень кратко касались взаимодействия объектов, регионов, поверхностей и окрестностей с аналогичными объектами других покрытий. Но большинство объектов, встречающихся в одном покрытии тоже имеют определимые характеристики пространственного расположения, которые могут указывать на механизмы их возникновения. По традиции, термин "пространственное распределение" обычно относится к простому картографическому отображению пространственно распределенных объектов. Исходя из парадигмы сообщения, мы могли бы сказать, что карта показывает, где объекты находятся и каковы очертания занимаемой ими области. Можно было бы сказать, что этого достаточно. Но интуитивно мы понимаем, что есть что-то ещё, помимо того, что может быть использовано для описания взаимодействий каждого отдельного объекта с его соседями и отношения всех этих объектов ко всему пространству, в котором они расположены. И, конечно, если мы сможем найти способы измерения этих отношений, то сможем найти пути выявления и понимания возможных механизмов, которые создают эти распределения. Одни из рассматриваемых методов - вычислительно просты, другие -очень сложны и требуют много машинного времени. Одни применяются очень часто, другие, хотя и чрезвычайно полезны, не получили широкого признания, так как о них редко рассказывают, за исключением аспирантур. Эту тему можно было бы проигнорировать, но я чувствую себя обязанным дать вам возможность пораньше узнать об этих методах анализа распределения объектов в пределах одного покрытия. РАСПРЕДЕЛЕНИЯ ТОЧЕК Возможно, наиболее распространенные методы анализа пространственных распределений применяются к точечным паттернам. Точечными объектами могут быть отдельные деревья, дома, животные, фонари и даже города, в зависимости от масштаба (Рисунок 11.1а). Как мы увидим в дальнейшем, точечные объекты могут также представляться в виде линий и областей (Рисунок 11.1b). 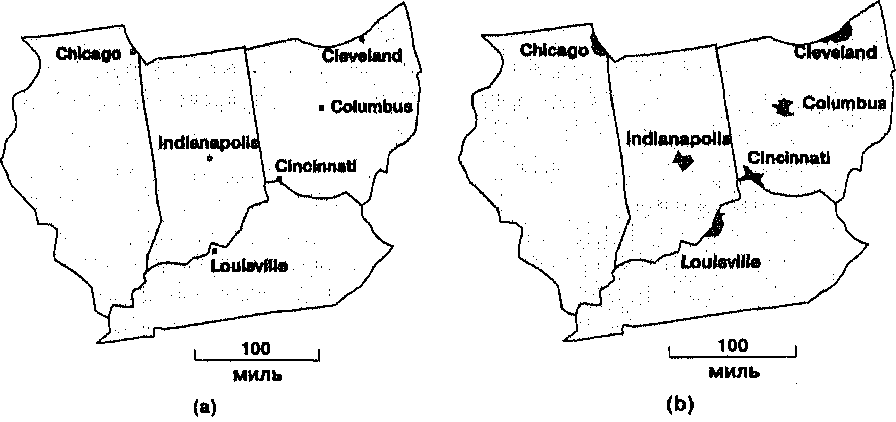 Рисунок 11.1. Точечное и площадное представление городов. Площадные объекты, в данном случае города, могут рассматриваться как точки (а) или как области (b), в зависимости от масштаба, в котором они представлены. Это указывает на связанность аналитических методов, которые могут применяться. Простейшей мерой точечного распределения является плотность (density) точек. Она определяется как результат деления числа точек на общую площадь, на которой они расположены. Плотности населения, застройки, деревьев и т.д. широко используются как меры компактности точек. Сравнивая плотности подобных объектов в разных областях, мы можем сравнивать механизмы, которые действуют в этих областях. Или мы могли бы сравнивать точки в том же месте, но в разные моменты времени, чтобы увидеть изменения плотности во времени. Например, мы могли бы обнаружить, что плотность населения в городской местности со временем растёт, или что растёт плотность застройки, или что плотность деревьев снижается по мере их развития и роста конкуренции за пространство и солнечный свет. Даже этот простой статистический показатель, легко вычисляемый на растре и векторах, может дать нам множество полезных идей о наших данных. Помимо общей плотности распределения, нас может интересовать еще и его форма. Точечные паттерны встречаются в одном из четырех возможных вариантов, характеристик. Распределение является равномерным (uniform), если число точек на единицу площади в каждой малой подобласти такое же, как и в любой другой подобласти. Если точки расположены в узлах сетки, разделенные одинаковыми интервалами по всей области, то равномерное распределение называется регулярным (regular), подобно рассмотренной ранее регулярной сетке отбора точек данных на поверхности. В других случаях равномерно распределенные точки располагаются в случайном (random) порядке по всей рассматриваемой области. Бывают случаи, когда точки собраны в тесные группы, такое распределение называется сгруппированным или кластерным (clustered) (см. Рисунок 2.8). Анализ квадратов Равномерные точечные распределения определяются на основе отношений между одинаковыми подобластями, называемыми квадратами (quadrats). Это очень распространенный метод анализа дискретных зоологических и агрономических данных. Точками здесь могут быть отдельные растения, муравейники и т.д. Если каждый квадрат содержит примерно одинаковое число точек, то распределение является равномерным. Равномерные распределения редко встречаются среди биологических явлений, так как живым организмам свойственно мигрировать в сторону большей концентрации питательных веществ, лучшего орошения, определенного типа почвы и т.д. Если распределение действительно равномерное, то мы можем предположить, что нет существенного механизма, управляющего расположением объектов. В стандартном методе анализа квадратов (quadrat analysis) [для равномерного распределения] мы предполагаем, что примерно одно и то же число объектов будет находиться в каждой подобласти, равное общему числу объектов, поделённому на количество подобластей. Для проверки равномерности распределения может использоваться относительно простой статистический показатель, который называется критерием х2 (хи-квадрат) (chi-square test) и выражается формулой: X2 = S[(Q-E)/E], где Q - наблюдаемое число точек в квадрате, Е - ожидаемое число точек в квадрате; суммирование проводится по всем квадратам. Результат этого вычисления может быть сравнен с табулированными критическими величинами. Если полученное число незначительно отличается от ожидаемого, то распределение является равномерным; заметное отличие говорит о некоторой неравномерности, что может означать наличие какого-то процесса, лежащего в основе неравномерности. Хотя этот метод может считаться чисто статистическим, он может быть реализован в некоторых ГИС, особенно в растровых. Такой анализ могут выполнять и многие специализированные программы. Если вы не знакомы со статистикой, особенно применительно к пространственным данным, то можете заглянуть в какую-нибудь простую книгу на данную тему, например, [McGrew and Monroe, 1993]. Сейчас же достаточно помнить, что чем больше значение X2, тем ниже равномерность распределения. Хотя результатом анализа в ГИС обычно считается карта, в данном случае результатом является одно лишь число. Здесь уместен такой вопрос: "Если распределение не равномерно, то какой механизм может быть ответственен за это?" Чаще всего наблюдаемые нами точечные паттерны связаны с другими показателями (покрытиями) карты той же области исследования. Эти возможно связанные покрытия могут быть не только точечными, но и площадными. В нашем примере с биологией это могли бы быть параметры почв. Это приведет нас к сравнению точек одного покрытия с полигонами другого, что является уже темой следующей главы. Помимо информации о равномерном распределении анализ квадратов может дать кое-что ещё. Например, отношение дисперсии к среднему (математическому ожиданию) (variance-mean ratio (VMR)), [McGrew and Monroe, 1993]. Здесь также используется критерий x2, который вычисляется как произведение отношения дисперсии к среднему на число подобластей за вычетом одной. Высокие значения x2 указывают на большой разброс между числом точек в каждой области и средним для всей области, то есть на то, что мы имеем кластерное (групповое) распределение [McGrew and Monroe, 1993]. И наоборот, малые значения x2 означают, что распределение более равномерное. Промежуточные значения указывают на то, что распределение более тесно связано с некоторым случайным процессом, где некоторые квадраты имеют несколько большее, а другие - несколько меньшее число, чем среднее. Как и раньше, результаты анализа говорят, что если распределение не является статистически случайным (т.е. если оно либо равномерное, либо кластерное), то вы можете попытаться определить возможную причину, разумно выбрав набор показателей для сравнения с вашим точечным покрытием. Например, равномерные распределения могут быть регулярными, как плодовые деревья в саду, или случайными, что более свойственно деревьям в лесу. В первом случае в каждой подобласти будет встречаться одинаковое число точек, во втором случае числа будут разными. Анализ ближайшего соседа До сих пор мы описывали точечные распределения количеством точек в пределах подобластей. Другими словами, мы рассматривали распределение точек посредством сравнения областей, которые они занимают. Однако, также поучительно рассмотреть локальные отношения внутри пар точек. Чаще всего это делается другим методом анализа точечных распределений - анализом ближайшего соседа (nearest neighbor analysis), общепринятой процедурой определения расстояния от каждой точки до ее ближайшего соседа (РБС) и сравнения этой величины со средним расстоянием между соседями. Вычисление этого статистического показателя включает определение среднего РБС среди всех возможных пар близколежащих точек (такие точки определяются как ближайшие к выбранной). Среднее РБС дает меру разреженности точек в распределении. Это ценно само по себе, так как в некоторых случаях точечные объекты могут конфликтовать, если они расположены слишком близко друг к другу. Например, мы знаем, что многим животным требуется определенное жизненное пространство, и когда оно перекрывается с пространством другого представителя того же вида, возможен конфликт. Но, как и в анализе квадратов, мы можем сравнить среднее РБС с тремя возможными распределениями - регулярным, случайным и кластерным. Этот метод может быть описан в общем [детально - см. McGrew and Monroe, 1993] для каждого из этих случаев как вычисление индекса, с которым вы можете сравнить свои результаты, как это указано далее. Для индекса случайного распределения поделите 1 на удвоенный квадратный корень из плотности точек (число точек на единицу площади). Если вам нужен критерий максимальной рассеянности (dispersion) (регулярное распределение), то поделите 1.07453 на квадратный корень из плотности точек. Наконец, для критерия максимальной сгруппированности, когда точки расположены одна под другой, мы можем просто принять, что величина получается делением на ноль (the value is of the divisor 0). В результате мы получаем некоторое неотрицательное значение индекса. Простое сравнение вашего среднего РБС с тремя индексами даст вам понятие о том, в каком месте диапазона они находятся. Давайте рассмотрим, как это работает на примере данных Таблицы 11.1 и Рисунка 11.2. У нас есть шесть точек, данных в пределах площади в 25 квадратных единиц. Среднее РБС этих данных составляет примерно 1.4. Для случайным образом распределенных данных индекс составит (единица, поделенная на удвоенный корень из плотности точек (6 точек на 25 единиц площади = 0.24), т.е. 1/(2 ^0.24) = 1.02. Наше среднее РБС несколько больше, чем этот индекс. Таблица 11.1. Вычисление расстояния до ближайшего соседа
Критерий максимальной рассеянности точек составит 1.07453, поделенное на квадратный корень из плотности точек, т.е. округленно 2.19. Таково было бы значение, если бы наше распределение точек было идеально равномерным. Наше среднее РБС намного меньше этого, но и намного больше, чем 0, который соответствует идеально сгруппированному распределению. Таким образом, мы нашли, что наше распределение несколько более рассеянное, чем случайное, или где-то между истинно равномерным и случайным. Другими словами, оно начинает принимать более регулярную конфигурацию, но пока все еще довольно случайное. РБС является абсолютным статистическим показателем, следовательно, он не может непосредственно сравниваться с РБС других точечных распределений. Индекс ближайшего соседства может быть нормализован для выполнения таких сравнений [McGrew and Monroe, 1993], но это уже выходит за рамки данной книги. Существуют также и другие методы определения кластеризации, основанные на других статистических показателях [Davis, 1986; Griffiths, 1962, 1966; Ripley, 1981], но это также выходит за рамки данной книги. 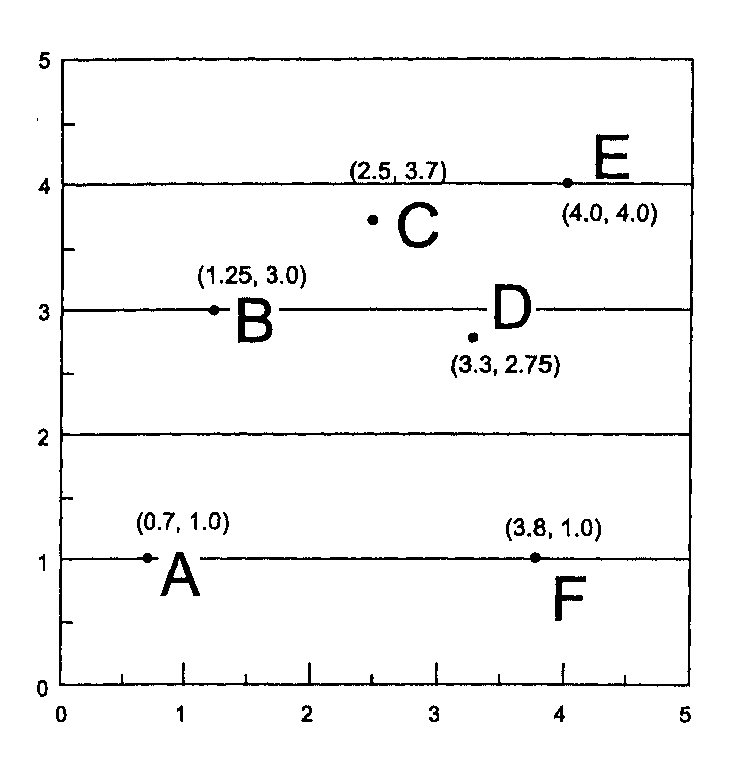 Рисунок 11.2. Координаты точек для определения РБС. Каждая точка (например, точка А) имеет своего ближайшего соседа (в данном случае, точка В). Расстояния определяются с помощью теоремы Пифагора (см. Таблицу 11.1). ПОЛИГОНЫ ТИССЕНА Точечные распределения могут также характеризоваться с помощью полигонов Тиссена (Thiessen polygons) (называемых также диаграммами Дирихле (Dirichlet diagrams) и диаграммами Вороного (Voronoi diagrams)). Они основаны на идее, что мы можем нарастить полигоны вокруг точек, чтобы показать их возможные зоны влияния на другие точки покрытия. Например, как мы увидим при работе с моделью гравитации, можно считать, что между точками действуют силы притяжения. Вдобавок, размер точки - например, города - часто напрямую связан с силой такого влияния. Мы ограничимся случаем равной величины всех точек, что упрощает описание. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
