Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
НАПРАВЛЕННОСТЬ ЛИНЕЙНЫХ И ПЛОЩАДНЫХ ОБЪЕКТОВ Линейные объекты могут характеризоваться не только распределением по ландшафту, но и ориентацией. Такие объекты как осадочные напластования, русла ледников, переносимая водой галька, цепи валунов, оставленные ледниками, ограждения, сети улиц, ветровал деревьев в лесу имеют определенную ориентацию, которая часто указывает на породившую их силу. Но когда мы анализируем ориентацию, у нас может возникнуть ситуация выбора между двумя встречными направлениями. Если линейный объект является улицей с односторонним движением, то ориентация ее самой не говорит нам о направлении, в котором должен двигаться транспорт. Поэтому, кроме ориентации нам нужно знать и о направленности (directionality). Мы можем также рассматривать распределения линейных объектов либо как двухмерные, либо как трехмерные, с учетом углового направления относительно поверхности сферы [Davis, 1986]. Для простоты мы ограничимся лишь первыми. В традиционном статистическом анализе ориентации линий с карты переносятся на диаграмму направлений (rose diagram), где все они прочерчиваются из одной начальной точки. На некоторых диаграммах направлений длиной линий также изображают параметры объектов, такие как сила ветра или длина изгороди. Диаграммы направлений полезны для визуальной оценки, но измерения, получаемые непосредственно поданным покрытия больше подходят для численного анализа. Первым мы рассмотрим равнодействующий вектор (vector resultant). В качестве примера можно вспомнить басню про лебедя, рака и щуку. Зная силы и направления, приложенные к возу, можно определить, в какую сторону и с каким ускорением объект начнет движение. Для демонстрации двухмерного анализа направлений возьмём большое количество деревьев, поваленных прямолинейным ветром. Каждое дерево может быть отображено как линейный объект покрытия, при этом записываются координаты вершины и основания каждого дерева, давая нам ориентацию каждого дерева (Рисунок 11.7). 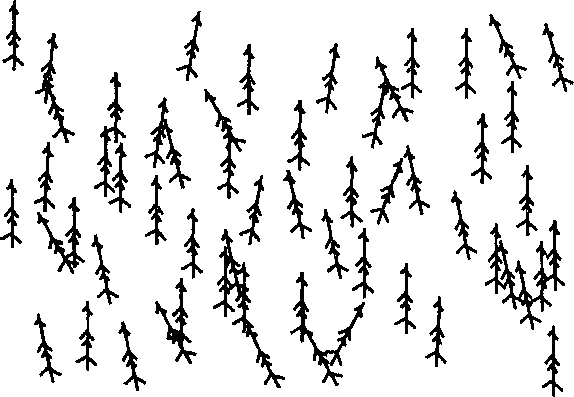 Рисунок 11.7. Распределение направлений поваленных деревьев. Карта показывает общую тенденцию и некоторые отклонения от нее. Метеорологи хотят выяснить общее направление ветра по поваленным деревьям, но эти деревья не имеют единой для всех ориентации, поэтому нашей первой задачей является определение равнодействующего вектора поваленных деревьев. С каждым деревом ассоциируется вектор с началом в основании дерева и углом Q в сторону вершины. Мы умножаем длину каждого дерева на косинус этого угла для получения Х-составляющен, а также на синус этого угла для получения Y-составляющей. Для вычисления равнодействующего вектора мы складываем эти величины для каждой составляющей, и полученные значения равнодействующего вектора Хг и Yг показывают преобладающее направление вершинных точек деревьев в ветровале. Рисунок 11.8 показывает равнодействующий вектор R, полученный из трех векторов А, В и С. Мы можем определить среднее направление Q исходя из равнодействующего вектора по формуле: Q = arctan (Yr/Xr). 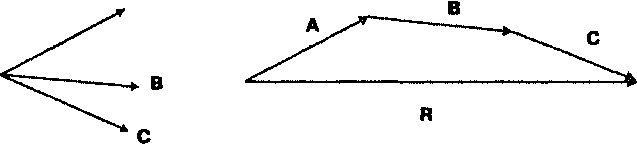 Три вектора Равнодействующий вектор Рисунок 11.8. Равнодействующий вектор. Так как среднее направление наших векторов зависит не только от разброса деревьев, но и от числа наблюдений, мы можем нормализовать эти величины делением координат каждого равнодействующего вектора на число линейных объектов покрытия. Это позволит нам сравнивать две различные области, например, две области ветровала на предмет общего направления ветра*. * Следует отметить, что здесь угол отсчитывается от оси Y, а не от оси X, как принято в математике. В формуле вычисления составляющих длина дерева является весовым коэффициентом для его направления. Чтобы каждое дерево вносило одинаковый вклад, следует приравнять его длину единице. Тогда среднее направление будет равно арктангенсу отношения суммы косинусов к сумме синусов направлений деревьев. Для данного примера можно также отметить, что более длинные деревья скорее всего будут лучше представлять среднее направление, так что нормализация будет излишней. — прим, перев. Как и с любым набором точек, где средняя величина служит мерой центральной тенденции данных или тенденции данных группироваться вокруг некоторой центральной точки, мы можем использовать среднее для получения других статистических показателей, которые определяют разброс от среднего. Рисунок 11.9 показывает два случая равнодействующего вектора R с тремя исходными. Когда векторы расположены близко к одному направлению, равнодействующий вектор будет длинным, в то время как при широко разбросанных исходных векторах - значительно более коротким. В нашем примере из басни это выглядит как сложение усилий участников в общем направлении или же скорее противодействие друг другу, приводящее к существенно меньшей равнодействующей силе, прилагаемой к возу. 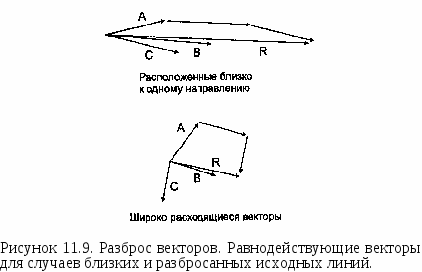 Длина равнодействующего вектора (resultant length) может быть определена по формуле: Таким образом, мы имеем не только среднее направление лесовала, но и меру компактности распределения: чем компактнее распределение, тем длиннее эта линия. Для сравнения длины равнодействующего вектора в данном месте с другим местом, нам следует, опять же, нормализовать данные. Нормализованная длина равнодействующего вектора получается делением длины равнодействующего вектора R на сумму длин образующих его векторов. Это безразмерная величина в диапазоне от 0 до 1, напоминающая дисперсию в традиционной статистике, так как является мерой пространственного разброса вокруг среднего значения. Правда, она выражает этот разброс "наоборот": большие значения соответствуют более близкой ориентации векторов, меньшие - большему разбросу. Таким образом, большое значение этого показателя в нашем примере с деревьями означало бы значительное преобладание одного из направлений ветра, а малое значение говорило бы о наличии завихрений или отсутствии явно преобладающего направления. Наряду с самой этой величиной можно использовать также и обратную ей величину, называемую круговой дисперсией (circular variance), которая равна единице минус нормализованная длина равнодействующего вектора. Если вы интересуетесь статистикой, то можете увидеть возможность существования дирекционных аналогов стандартного отклонения, моды и медианы, для которых также имеются соответствующие формулы [Gaile and Burt, 1980]. Остается одна проблема, связанная с ориентацией и направлением. Как мы знаем, одни линейные объекты могут иметь определенное направление (деревья), другие же - нет (лесозащитные полосы), хотя определенная ориентация присутствует в обоих случаях. Например, один исследователь, собирающий данные о заграждениях, может указывать, что некоторые из них ориентированы на север, а другой - что на юг. Тогда, при анализе данных, собранных этими исследователями, может оказаться, что при определении длины среднего равнодействующего вектора, исходные векторы будут, так сказать, взаимно уничтожать друг друга. К счастью, для этого есть остроумное решение. Крумбейн [Krumbein, 1939] обнаружил, что при удвоении значения угла, независимо от исходного направления, записывается одно и то же значение. Допустим, мы имеем объект, ориентированный с северо-запада (315°) наюго-восток(135°). После удвоения мы получим: 315° х 2 = 630° (-360° = 270°) и 135° х 2 = 270°. Такой способ выражения направлений повлияет на формулы для вычисления среднего направления, нормализованной длины равнодействующего вектора и круговой дисперсии, поэтому, чтобы получить действительные значения, их нужно будет модифицировать. Эти простые меры направленности и разброса могут быть проверены на случайность [Batschelet, 1965; Gumbelet al., 1953] и наличие тренда [Stephens, 1969] стандартными процедурами проверки статистических гипотез. С дирекционными данными покрытия могут сравниваться аналогичные данные других покрытий [Gaile and Burt, 1980; Mardia, 1972]. Эти темы выходят за рамки данной книги, а указанные источники предлагают подробное их рассмотрение. В контексте ГИС, данные меры главным образом помогают охарактеризовывать распределения внутри покрытия и сравнения их с данными других покрытий в поисках причинных механизмов. Растровые ГИС плохо приспособлены для данного типа анализа, но большинство векторно-топологических систем позволяют определить по меньшей мере некоторые предварительные значения (например, углы отрезков полилиний), которые могут храниться в БД ГИС как атрибуты и передаваться другим программам для обработки, если сам ГИС-пакет не способен вычислять средние показатели направленности. СВЯЗНОСТЬ ЛИНЕЙНЫХ ОБЪЕКТОВ Важным аспектом пространственного расположения линий является их способность образовывать сети. Сети имеют самые разнообразные формы, как естественные, так и созданные человеком. Среди них: автомобильные и железные дороги, телефонные линии, реки, даже лесозащитные полосы могут играть роль сети, позволяющей мелким млекопитающим перемещаться по ландшафту, - список можно долго продолжать. И хотя мы можем интересоваться плотностью и ориентацией объектов, образующих сеть, нам нужна также и возможность анализировать реальные связи, образованные этими объектами и степень связанности между различными точками сети. Вы наверняка сталкивались с ситуациями, когда в городе нет прямой дороги от места до места, и приходится ехать кружным путем. Здесь мы сталкиваемся с недостатком связности (connectivity) в сети. Связность является мерой сложности сети. Имеются несколько методов для определения этой характеристики [Haggett et al., 1977; Lowe and Moryadas, 1975; Sugihara, 1983; Taaffe and Gauthier, 1973]. Наиболее общими являются гамма-индекс (gamma index) и альфа-индекс (alpha index). Гамма-индекс у является отношением числа существующих связей между парами узлов сети, L, к максимально возможному числу связей в том же наборе узлов, Lmax. Очевидно, что векторно-топологическая модель данных лучше всего подходит для этих вычислений. Определить же не так трудно, как может поначалу показаться, оно однозначно определяется числом узлов V. Например, если мы имеем три узла, то возможны лишь три связи (Рисунок 11.10). Если мы добавим еще один узел, то сможем добавить еще три связи, а всего их будет шесть [Forman and Godron, 1987]. И если мы полагаем, что не образуются новые пересечения, то максимальное число связей будет каждый раз увеличиваться на три. То есть, Lmax= 3(V - 2). Гамма-индекс тогда определяется как Y = L/Lmax = L/3(V-2) Он принимает значения от 0 (нет ни одной связи) до 1 (все возможные связи присутствуют) [Forman and Godron, 1987]. Рисунок 11.10 показывает два варианта сети с 16-ю узлами. На рисунке
Большее количество связей в сети облегчает передвижение по ней, что важно, например, для специалистов по транспортному планированию. Важной характеристикой сетей помимо связности является наличие в ней контуров, позволяющих перемещаться от узла к узлу разными маршрутами. В качестве примера можно привести кольцевые автодороги вокруг крупных городов, позволяющие снизить нагрузку транзитного транспорта на уличную сеть. 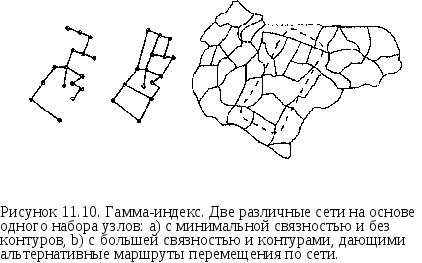 (а) (b) (с) (а) (b) (с) В качестве меры соединенности узлов контурами альтернативных маршрутов (circuitry) используется так называемый альфа-индекс (а). Он является отношением имеющегося в сети числа контуров к максимально возможному числу контуров в этой сети. Известно, что сеть без контуров имеет связей на одну меньше, чем число узлов: L = V - 1. На Рисунке 11.10а вы можете видеть такую сеть, - в ней 16 узлов и 15 связей. Она обладает минимальной связностью, в том смысле, что в ней имеется наименьшее возможное число связей при заданном числе узлов, причем каждый узел имеет по меньшей мере одну связь. Добавление какой-либо связи создает контур, т.е. когда сеть содержит контуры L > V - 1. Число же имеющихся контуров можно определить как L -(V-1) [Forman and Godron, 1987]. Далее, так как максимальное число связей в сети определяется как 3(V -2), а минимальное (без потери связности) как V - 1, то максимальное число контуров будет 3(V - 2) - (V - 1), т.е. 2V - 5. Отсюда альфа-индекс а = (L - (V -1)) / (2V - 5). Диапазон значений альфа-индекса - от 0 (сеть без контуров) до 1 (сеть с максимальным числом контуров). Теперь мы можем вычислить альфа-индекс для сетей на Рисунке 11.10: а = (15 - 16 + 1) / (2 х 16 - 5) = 0 а = (20- 16 + 1)/(2х 16 - 5) = 0.19 Таким образом, в сети на Рисунке 11.10а есть только один вариант для перемещения из одной точки в другую, а на Рисунке 11. 10b возможны несколько альтернативных маршрутов разной длины. Поскольку для создания контуров требуется добавление новых связей, вполне возможно рассматривать альфа-индекс как альтернативную меру связности. Но так как эти два индекса дают разные взгляды на сеть, будет более уместным объединить их некоторым образом для создания общей меры сложности сети (network complexity). Для вычисления данных индексов требуется использование векторной ГИС. Это требование подчеркивается тем обстоятельством, что вся эта статистика имеет топологическую основу теории графов, где гораздо важнее связность узлов, нежели их расположение или длины и формы линий, связывающих их. Для транспортного моделирования нам нужно знать все-таки больше, чем просто параметры связности. Здесь имеют значение длины связей между узлами, возможные направления движения по этим линиям, значения сопротивления движению (импеданса). Вдобавок, существуют и другие простые индексы, пришедшие из теорий транспортировки и связи, которые также характеризуют связность сетей. Например, возможно определение интенсивности связности (linkage intensity) для каждого узла, числа альтернативных маршрутов между заданными узлами, поиск центрального узла (central place), т.е. такого, который имеет наибольшее число связей, а также построение регионов на основе связности и доступности [Haggett et al., 1977; Lowe and Moryadas, 1975]. И все это можно сочетать друге другом и с другими характеристиками линий - расположением, ориентацией, дисперсией - для получения более полной картины сети. МОДЕЛЬ ГРАВИТАЦИИ До сих пор мы не обращали внимание на значимость отдельных узлов, которая может быть неодинаковой. Но подумайте о городах. Крупные города по сравнению с мелкими дают больше возможностей для покупок, для посещения выставок, концертов, спортивных соревнований и т.д. Поэтому они привлекают больше людей. И города - не единственный пример, когда размер имеет значение. Например, большое озеро привлекает больше водоплавающих птиц, нежели маленький пруд. Оба примера показывают, что более крупные объекты привлекают к себе большую активность, будь то птичью, или человечью. Размер такого притяжения может представляться во многом подобно гравитационному притяжению тел, обладающих массой. Чем больше масса, тем больше сила притяжения между ним и его соседями. Перенося идею гравитационного притяжения на взаимодействие между узлами покрытия ГИС, мы получим модель гравитации (gravity model), которая в общем виде выражается как: где Lij - величина взаимодействия между узлами i и j; Рi - величина узла i; Pj - величина узла j; d - расстояние между узлами; К - константа, определяемая природой взаимодействующих объектов. Величины узлов могут быть представлены такими их параметрами, как потребность в продукции, объем розничных продаж торговых центров города, площадью поверхности водоема для водных птиц. Мы видим, что чем больше величины узлов, тем больше сила взаимодействия между ними, и что с ростом расстояния между узлами сила взаимодействия уменьшается. На примере города мы можем сказать, что чем больше город, тем более он привлекателен для торговли. С другой стороны, если город находится далеко от вас, вряд ли вы в него поедете, даже несмотря на возможную выгоду от сделки. [Как говорит русская поговорка, "за рекой телушка — полушка, да рупь перевоз".] Существуют многие варианты данной простой модели притяжения между точками, как в растровых, так и в векторных системах. И хотя большинство из них используется для экономического анализа размещения объектов (также как и полигоны Тиссена), возможно и другое их применение. Исследователи могут использовать их для описания пассажиропотока между городами, объема телефонных вызовов, потоков птиц и семян, которые распространяются птицами между участками леса [Buell et al., 1971; Carkin et al., 1978; McDonnell, 1984; McQuilkin, 1940; Whitcomb, 1977]. В-общем, любые потоки между узлами различной величины могут анализироваться с применением модели гравитации. МАРШРУТИЗАЦИЯ И АЛЛОКАЦИЯ Среди наиболее применяемых приложений сетей в ГИС являются родственные задачи маршрутизации и размещения (аллокации) (routing and allocation). Простейший вариант маршрутизации включает поиск кратчайшего маршрута между двумя узлами сети (Рисунок 11.11). Учитывая, что узлам могут присваиваться весовые коэффициенты (как в модели гравитации), возможен вариант маршрутизации от некоторой заданной точки до ближайшей точки с максимальным весом (например, максимальным спросом на товар). Прекрасное описание маршрутизации и размещения можно найти в [Lupien et al., 1987]. Каждой связи в сети может быть присвоено значение импеданса (сопротивления, стоимости), во многом наподобие фрикционной поверхности, но налагаемого только на саму эту линию. Значение импеданса может быть связано, например, с ограничением скорости или даже запретом проезда по некоторым улицам, как, например, в случае закрытия дороги на ремонт. Используя нарастающее расстояние (accumulated distance) (см. Главу 8), с учетом как геометрического расстояния, так и значений импеданса, может строиться наиболее эффективный маршрут (т.е. маршрут наименьшей стоимости), а не просто кратчайший. Узлам также могут присваиваться значения импеданса или стоимости и запреты на их прохождение. Как и при определении функциональных расстояний на поверхности и стоимости передвижения по ней, все это требует априорного знания свойств улиц, перекрестков и других узлов. И нередко бывает так, что веса и импедансы задаются несколько произвольно или по интуиции. 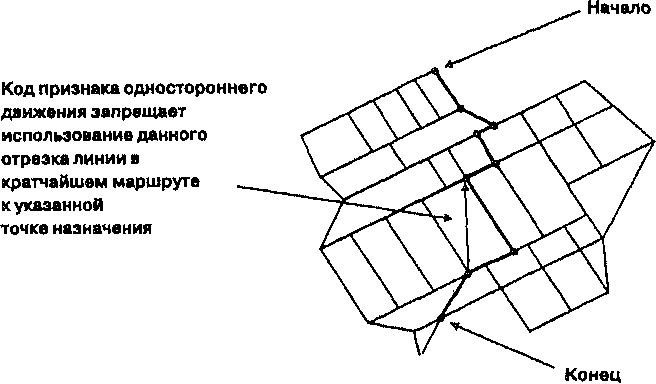 Рисунок 11.11. Кратчайший маршрут в сети. Результат работы алгоритма поиска кратчайшего маршрута в простой дорожной сети. Хотя маршрутизация в принципе может выполняться на растре, она гораздо легче реализуется в векторной топологической модели данных, поскольку эта модель лучше других воспроизводит характеристики графов. Вам также следует знать, что вследствие наличия контуров в сети, возможны альтернативные маршруты между двумя заданными точками, а с учетом различных ограничивающих факторов, как статических (свойства дороги), так и динамических (наличие уже существующего движения), плюс различные виды оптимизации маршрутов (посещение набора узлов в заданном порядке, оптимизация использования парка транспортных средств, организация работы по обслуживанию множеств поставщиков и потребителей грузов, выравнивание нагрузки на дорожную сеть и т.д.) тема маршрутизации заслуживает отдельной толстой книги. Аллокация (allocation) это процесс, который может использоваться для определения, например, положения нового супермаркета, территориального покрытия станции водоочистки, или границ зон обслуживания противопожарных частей. Чаще всего при этом используется сетевая структура в векторной ГИС. Идея состоит в распространении возможностей заданной службы по сети. Каждая связь (или каждый узел) сети имеет определенное число обслуживаемых элементов. Например, каждый отрезок улицы имеет некоторое число домов, к которым подается вода. Каждый дом может рассматриваться также как потенциальный клиент для близлежащей противопожарной части [Lupien, et al., 1987]. Кроме того, каждая служба или каждый торговый центр имеют определенную максимальную нагрузку и предельное расстояние обслуживания, а срочные службы — ограничение по времени на обслуживание одного обращения; все это также учитывается при построении зон обслуживания (Рисунок 11.12). Если бы дорожная сеть была совершенно однородна (без импеданса, запретов, ограничений скорости и т.д.) аллокация была бы просто делом выбора критерия и расширения границ зон обслуживания от центров, пока эти границы не встретятся. 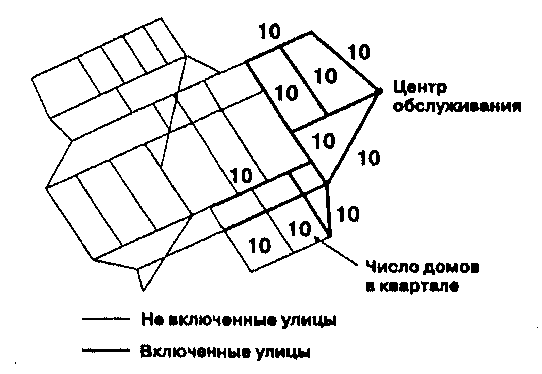 Рисунок 11.12. Аллокация в сети. Приписывание улиц, каждая из которых имеет по 10 домов к центру обслуживания, способному надежно обслуживать только 100 домов. Например, если бы мы проводили аллокацию для распространителей газет, так чтобы машина каждого проходила только определенное число километров, программе пришлось бы просто подсчитывать километры, когда маршрут расширяется от начальной точки, пока не будет достигнут заданный километраж, после чего улицам будут присвоены соответствующие коды атрибутов распространителей. Как вы могли догадаться, большинство реальных задач аллокации Пространственные распределения довольно сложны, и на эту тему написаны серьезные труды. Здесь только следует еще упомянуть о связи почтовых адресов с линейными объектами, образующими покрытие уличной сети. Установление такого соответствия называется адресным геокодированием (address matching). Оно позволяет определять почтовый (логический) адрес по географическим или условным координатам объекта или топологическим координатам в сети, а также выполнять обратные преобразования. Его необходимость обусловлена тем, что люди используют логические адреса, в то время как ГИС оперирует координатами и топологией. НЕДОСТАЮЩЕЕ ЗВЕНО: ПОЧЕМУ НУЖНО ИСПОЛЬЗОВАТЬ ДРУГИЕ ПОКРЫТИЯ Здесь нужно лишь одно простое замечание. К настоящему моменту мы рассмотрели, как точечные, линейные и площадные объекты могут исследоваться на предмет их распределения, связности и ориентации, образования ими окрестностей. Однако, все эти аналитические операции часто имеют смысл только при соотнесении их с анализом других покрытий, что особенно верно для поиска причинных механизмов рассматриваемых явлений и определения влияния одних объектов на другие. В следующей главе мы займемся этими вопросами, которых и им подобных, на самом деле, гораздо больше, чем можно было бы подумать. Вопросы
Наложение покрытий Процесс наложения требует сравнений как графики, так и атрибутов. Техника выполнения наложения может быть довольно сложной, особенно в отношении алгоритмов, связанных с выполнением векторного наложения. Последующие графические описания процесса наложения должны дать вам понимание того, как компьютер выполняет векторное наложение. Данная глава дает общее, на уровне идей, понимание вопроса, она не детализирует все возможные методы логического или математического комбинирования покрытий, но фокусируется на некоторых из них, которые должно быть не трудно понять. При возможности, вы можете опробовать различные методы на одном и том же наборе данных. Нет замены опыту, который даст вам понимание того, какой из методов наиболее пригоден для ваших задач. Опыт, приобретенный даже на простейшей ГИС, легко может быть распространен на более мощную систему. Время, затрачиваемое на освоение большой системы, может быть существенно сокращено, если вы уже знакомы с тем, как наложение выполняется, - вам потребуется только просмотреть страницы документации, относящиеся к слову "overlay" и определить, какие кнопки нажимать для запуска известных вам алгоритмов. КАРТОГРАФИЧЕСКОЕ НАЛОЖЕНИЕ К наиболее мощным возможностям современных ГИС относится их способность комбинировать картографическое представление тематической информации одной выбранной темы с другой. Этот процесс, называемый наложением (overlay), настолько интуитивно очевиден, что его применение за десятилетия предшествовало появлению современных компьютерных геоинформационных систем. Давайте рассмотрим такой пример. Новичок начинает работать в ГИС с десятками тематических покрытий на территорию своего округа. Среди них - стоимость земли, зонирование, типы почв, землепользование, дороги, естественная растительность, больницы, противопожарные станции, школы и т.д. Узнав, как выполнять наложение, он хочет попробовать его в действии, и вот, просматривая покрытия, он обнаруживает почти полное пространственное совпадение наиболее дешевых земель с распределением старовозрастных дубовых лесов. Отсюда можно сделать вывод, что этот вид лесов создает почвы низкого качества, что, в свою очередь, обуславливает их низкую ценность. Хотя это может быть действительно так, на самом деле рассматриваемая корреляция может быть обусловлена совсем другими факторами. И когда наш новичок создает наложение из покрытий стоимости земли и типов землепользования, он обнаруживает, что определенная категория землепользования, в данном случае - лесоводство, почти точно совпадает с областью старовозрастного леса. Не удивительно, что хотя эта земля имеет ценность для лесозаготовительной компании, ее стоимость гораздо ниже, чем стоимость земли в расположенных поблизости промышленных, торговых и жилых зонах. В этих покрытиях можно найти и многие другие корреляции, например, между стоимостью земли и транспортной инфраструктурой, землепользованием и зонированием, между пересечениями дорог и расположением заправочных станций. Однако, следует помнить о рискованности выносить суждения о причинно-следственных связях на основе обнаружения только лишь визуальной корреляции. И поскольку карту очень легко принять за истинную картину реальности, тем более важно получить доказательства реального существования таких связей, прежде чем они будут использованы. Теоретическая основа пространственной корреляции различных феноменов уже разработана для некоторых категорий картографических данных, но, конечно, не для всех. Например, Сойер [Sauer, 1925] создал модель взаимосвязи общих категорий данных о земле в своей работе по морфологии ландшафтов. Его исследование выявило существование значительной корреляции между человеческой активностью, формами ландшафта и другими физическими параметрами. Хотя он не формализовывал эти связи для применения на картах, очевидно, что он увидел связи между распределениями этих феноменов на земной поверхности. В дальнейшем исследователи формализовали эту разработку в виде широкого спектра подходов, названных, например, sieve mapping [Tyrwhitt, 1950; Hills et al., 1967]. Среди наиболее влиятельных разработчиков этого направления был Ян МакХарг (lan McHarg), работа которого, связанная с окружающей средой, породила целую школу мысли среди сегодняшних архитекторов ландшафтов, которая позволяет значительную часть работы выполнять при помощи компьютера, по сравнению с тем, что было возможно на основе полевых наблюдений и картографии одного покрытия [Simpson, 1989]. Он использовал некомпьютерный метод наложения с использованием прозрачной пластиковой пленки [McHarg, 1971], на отдельных листах которой отображались параметры окружающей среды: чем темнее участок пленки, тем выше чувствительность среды.  уклон Зона 1 свыше 10%. Зона 2 менее 10% и более 2.5%. Зона 3 менее 2.5%. ПОВЕРХНОСТНЫЙ сток Зона 1 Водные поверхности реки, озера, водохранилища. Зона 2 Каналы естественного стока и области ограниченного стока. Зона 3 Отсутствие водной поверхности или выраженных каналов стока. ПОЧВЕННЫЙ СТОК Зона 1 Солончаки, болота и другие низменности с плохим стоком. Зона 2 Области с высоким уровнем грунтовых вод. Зона 3 Области с хорошим внутренним стоком. ПОРОДЫ ОСНОВАНИЯ Зона 1 Заболоченные территории, наименьшее сопротивление сжатию. Зона 2 Меловые отложения: пески, глины, галечник, глинистый сланец. Зона 3 Кристаллические породы: серпентинит и диабаз. ПОЧВЫ Зона 1 Глина и суглинок, низкая стабильность и низкое сопротивление сжатию. Зона 2 Суглинки от мелкопссчаных до крупнопесчаных. Зона 3 Гравий или бурый суглинок и суглинок от гравийного до каменистого. ПОДВЕРЖЕННОСТЬ ЭРОЗИИ Зона 1 Все участки с уклоном более 10% с песчаной почвой. Зона 2 Почвы из песка и гравия или бурого суглинка и области с уклоном более 2.5% на суглинке от гравийного до каменистого. Зона 3 Прочие области мелкоструктурной почвы и малого уклона. Рисунок 12.1. Наложение пленок для определения чувствительности окружающей среды. Пример использования наложения пленок при ручном выполнении процесса наложения для демонстрации повышения чувствительности с ростом числа перекрывающихся категорий физических параметров. При наложении листов с покрытиями друг на друга чувствительность по разным параметрам складывается. В результате создавалось новое, суммарное, покрытие, которое могло быть использовано для рассмотрения альтернатив и принятия решений (Рисунок 12.1) [Steinitz et al., 1976]. Мы далеко не всё еще знаем о причинных связях пространственных феноменов. Эта тема является значительной частью того, чем занимаются географы. Геоинформационные системы дают теперь возможность легко выполнять процедуры наложения, благодаря чему могут возникнуть новые гипотезы, теории и даже законы об этих корреляциях. Многие специалисты из разных областей могут получить ценные сведения о пространственных корреляциях, которые ранее не наблюдались или даже не могли наблюдаться без применения компьютеров. По мере развития этого процесса мы будем получать все более детализированный набор правил о допустимости наложения покрытий и выводе утверждении о причинно-следственных связях. А пока нам следует быть внимательными, ибо современные ГИС позволяют использовать не один-единственный простой метод наложения, а десятки. Эти развитые возможности наложения легко могут привести к большому числу ошибок при сравнении не связанных покрытий и ошибочным выводам в результате. Следует заметить, что это также усиливает нашу способность сознательно искажать информацию на картах, причем в существенно большей степени, чем до того, как ГИС стали использоваться для сравнения пространственных феноменов [Monmonier, 1991]. ТОЧКА В ПОЛИГОНЕ" И "ЛИНИЯ В ПОЛИГОНЕ" Традиционно, как с использованием пленок, так и с применением компьютеров, наложение рассматривается как метод сравнения полигональных покрытий. Но существуют и другие типы наложений, использующие точечные и линейные данные. Рассмотрим пару примеров. Допустим, некий детектив пытается обнаружить пространственную связь между некоторыми районами города и участившимися случаями уличного воровства. Он не имеет возможности сбора данных на месте, но должен полагаться на записи сотрудников полиции о подобных случаях за последние годы. Он может также взять записи по преступности из имеющихся архивов и отметить адреса этих инцидентов на карте города, где также имеются границы районов. Это значит, что, отмечая по адресу точки происшествий, он тем самым помещает их в полигоны, представляющие районы города. Вдобавок, он отображает на карте статистику преступности за каждый месяц. Этот утомительный процесс был бы намного проще, если бы данные уже были включены в некоторую ГИС. Исследовав точечное распределение, он обнаруживает, что в районе Плезэнтфилд совершено гораздо больше уличных краж, чем где-либо еще. Это удивительно, ибо Плезэнтфилд - район не бедный, где можно было бы найти много нуждающихся в мелких суммах денег. Это также не богатый район, где жители могли бы носить с собой крупные суммы денег. Плезэнтфилд - район среднего класса, жители которого имеют средние доходы, скромные дома и семейные автомобили*. Возможно, в этом районе следует просто усилить полицейское патрулирование, но детектив не нашел еще главную причину повышенной концентрации здесь случаев уличного воровства. Тогда он начинает рассматривать годовые данные помесячно и обнаруживает повышенное количество краж в декабре. Зная, что в этом месяце имеет место активная предрождественская торговля, он решает сравнить данные этих месяцев с остальными за несколько лет. Двигаясь год за годом назад, он обнаруживает сохранение тенденции вплоть до 1983 года, до которого случаи уличного воровства имели большую рассеянность по районам города в противоположность концентрации в Плезэнтфилде. Год же 1983-й является годом завершения строительства торгового центра в Плезэнтфилде. Уже теплее! Далее он рассматривает точечные отметки случаев уличных краж на более подробной карте района и обнаруживает, что эти точки концентрируются вдоль дорог с интенсивным движением к торговому центру и от него. Это показывает на повышенное значение некоторых линейных объектов (улиц) внутри полигонов (районов). Наш детектив продемонстрировал сильную корреляцию между точечными и полигональными объектами, и мы видим, насколько полезным может быть сравнение между этими объектами. Он также установил определенную связь между данными в пределах одного покрытия. Анализируя карты, он обнаружил не только то, что в одном из полигонов оказалось больше точек, чем в других, но и то, что сами точки находились поблизости друг от друга (сгруппированное распределение) и от линейных объектов. * т.е. не персональные на каждого взрослого члена семьи, что обычно для богатых районов США — прим. перев. Следующий пример покажет возможность корреляции линейных и полигональных объектов, или процедуру "линия в полигоне" (line-in-polygon). Представьте себя в роли специалиста по исторической географии, занимающегося исследованием развития своего города. Вы знаете, что город испытывал несколько периодов активного роста, и что архитектурные решения, присущие различным периодам, заметно различаются. Вначале вы наносите на карту как отдельные полигоны области однородной архитектуры. Возникающее распределение показывает три крупных зоны, в которых расширение выглядит как длинные щупальца, исходящие из центрального ядра. Вследствие линейноподобной природы полигонов вы начинаете подозревать, что причиной такого распределения являются какие-то линейные объекты. Тогда вы составляете набор карт с участием наиболее заметных линейных объектов городской среды — транспортных сетей. Вы составляете карту железных дорог, карту со старыми трамвайными линиями, карту со скоростными шоссе. После переноса этих карт на пленки вы накладываете их на карты архитектурных периодов, чтобы разглядеть возможные соответствия. К вашей радости, вы обнаруживаете, что через полигоны раннего периода роста проходят крупные железнодорожные линии, которые существовали в то время. Затем вы накладываете слой с трамвайными линиями и видите аналогичное сходство для второго периода роста. Наконец, после наложения пленки с шоссе вы опять обнаруживаете пример сильной пространственной корреляции между доминирующими транспортными сетями и расширением городской территории [Adams, 1970] (Рисунок 12.2). 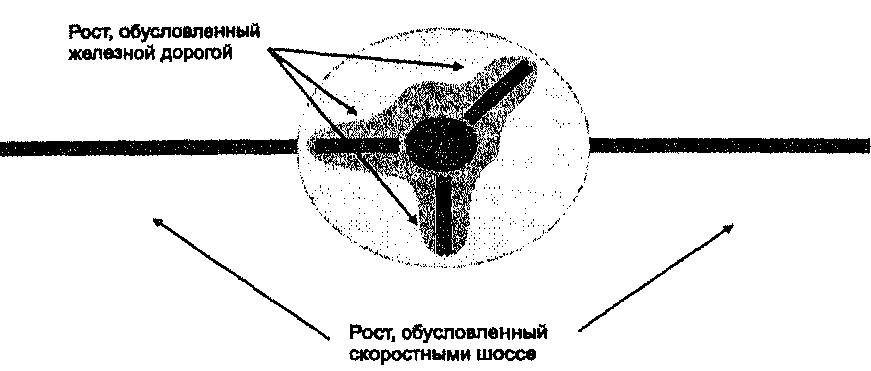 Рисунок 12.2. Линия в полигоне. Так могло бы выглядеть наложение "линия в полигоне", показывающее связь между полигонами расширения города и линиями доминирующих транспортных сетей. Результаты наложения помогут доказать, что наблюдаемые сходства пространственных распределений демонстрируют действие некоторого реального причинно-следственного механизма. Однако, при выполнении работ без применения ГИС потребуется немало времени на составление карт и рассмотрение многих покрытий. Кроме того, если вы хотите рассмотреть вдобавок к упомянутым еще и другие показатели, для них вам также придется составлять и накладывать слои карты. Если же в вашем распоряжении имеется ГИС с большим числом тематических слоев, то вы могли бы легко выполнить наложение любого набора из этих показателей, чтобы рассмотреть другие гипотезы о картине пространственного изменения города. К тому же, если вы сможете доказать существование функциональной зависимости между наблюдаемыми паттернами, это знание могло бы использоваться при планировании управляемого роста города. Компьютеризация этих простых методов географического анализа приносит как концептуальные, так и практические плоды. НАЛОЖЕНИЕ ПОЛИГОНОВ Как уже упоминалось, исторически сложилось так, что сравнение полигональных покрытий является наиболее распространенным подходом к выполнению наложения, вследствие чего разработчики геоинформационных систем изначально развивали именно этот тип наложения. Поэтому существуют различные подходы к выполнению наложения полигонов, ориентированных на определенные потребности пользователей. Рассмотрим пример использования наложения полигонов. Планировщик регионального уровня должен подготовить план контролируемого роста населения в сельской местности, которая должна подвергнуться интенсивной урбанизации в течение ближайших двадцати лет. При разработке плана рост может допускаться в тех областях, где имеются почвы, пригодные для строительства домов с фундаментами. При этом следует везде, где возможно, сохранять почвы высшего качества для ведения сельского хозяйства. Кроме того, следует предотвратить застройку земель, находящихся в собственности федерального правительства, земель, которые уже используются в качестве сельхозугодий, земель, на которых производятся археологические раскопки, а также земель, где находятся области обитания охраняемых видов животных. Следует также учесть, что нормативные акты позволяют местной администрации запрещать урбанизацию областей, предназначенных для других целей. Рассмотрев эти требования, планировщик собирает карты с названными темами и готовит пленки, каждая из которых содержит затемненные участки, соответствующие запрету урбанизации по соответствующему тематическому критерию, и прозрачные участки, где данный критерий разрешает застройку. После наложения всех этих пленок друг на друга затемненными окажутся участки, на которых нельзя вести строительство, так как они находятся на почвах, не пригодных для домов с фундаментами, или их почвы имеют большой агрономический потенциал, или они используются для сельского хозяйства, или там ведутся археологические раскопки, или на них расположены места обитания охраняемых видов животных, или они принадлежат федеральному правительству (Рисунок 12.3). Вы можете отметить, что все названные ограничения соединены союзом "или", выделенным жирным шрифтом, означающим в алгебре логики операцию "или" (дизъюнкцию), а в теории множеств - операцию объединения, в результате которой мы получаем покрытие, объединяющее все названные ограничения. 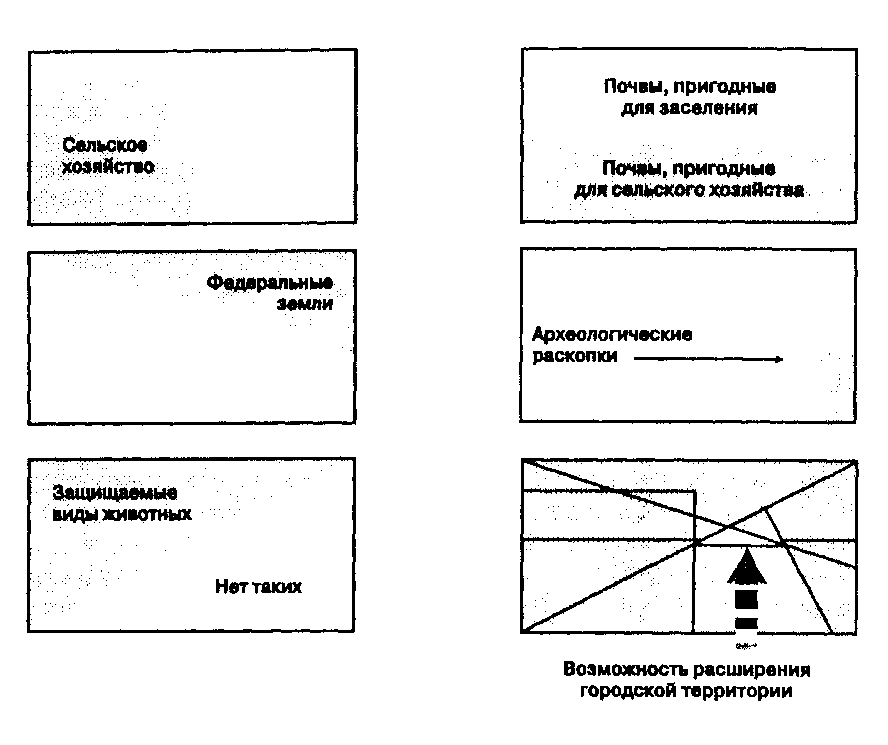 Рисунок 12.3. Наложение полигонов. После наложения затемненными будут те участки, на которых действует хотя бы одно из ограничений. Этот же пример можно рассматривать как применение логической операции "и" или операции пересечения множеств (это должно быть для вас очевидным, если вы знаете законы Де Моргана). Здесь мы обращаем внимание уже на прозрачные участки пленок, соответствующие отсутствию ограничений (отмечено словом "не"). То есть, в результате наложения останется прозрачной та часть карты, на которой можно вести строительство, так как там находятся почвы, пригодные для домов с фундаментами, и они не имеют значительного агрономический потенциала, и они не используются |
