Шпора по физике [3 семестр]. Интерференция света световая волна
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
ТЕПЛОВЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ТЕПЛОЕМКОСТЬ1) КЛАССИЧЕСКАЯ ТЕОРИЯ: при V=const, Cv=dEвн/dt. Т.к. коэффициенты объемной сжимаемости твердых тел малы, можно считать, что Cv=Cp=C (Cp – при P=const). Классическая теория теплоемкости исходит из положений: 1) Частицы, совершающие тепловые колебания в узлах кристаллической решетки, являются независимыми друг от друга и колеблятся с одинаковой частотой ν 0 = const. 2) колеблющуюся частицу в узлах кристаллической решетки следует уподоблять классическому гармоническому осцилятору. 3) энергия колеблющейся частицы распределяется равномерно и непрерывно между всеми степенями ее свободы. Тепловые колебания – единственный тип движения в котором участвует частица в узле кристаллической решетки, при этом приближение гармонического осцилятора справедливо, если сила, действующая на колеблющуюся частицу пропорциональна величине смещения F= -kx. Т.е. когда амплитуда колебаний не слишком велика полная энергия равна сумме кинетической и потенциальной E=К+П. Т.к. частота тепловых колебани велика, то даже за малый промежуток времени частица совершает большое число колебаний => можно считать, что средняя кинетическая энергия = средней потенциальной энергии за один и тот же промежуток времени, К(в)=П(в), K(в)=1/2 kT; П(в)=1/2 kT; i=1 (одна степень свободы), E=KT. Т.к. частица в узле кристаллической решетки обладает 3-мя степенями свободы i=3, то для одного грамма атома твердого вещества (для одного моля) E(в)=3kTN; C=dEвн/dt=3kN=3R. Т.о. теплоемкости химически простых твердых тел одинаковы и = 3R. Для большинства веществ этот закон выполняется при комнатной температуре и выше. При понижении температуры наблюдается отступление от закона Дюлонга-Пти. Расхождение с опытом обусловлено грубостью основных положений классической теории. 1) представление о том, что частицы в узлах кристаллической решетки являются независимыми друг от друга, колеблются с постоянной частотой. На самом деле все частицы в кристалле тесно связаны между собой и имеют дискретный энергетический спектр с широким набором частот собственных колебаний. 2) колеблющуюся частицу в кристалле следует уподоблять не классическому, а квантовому осцилятору, энергия которого, определяемая формулой Планка, должна заменить классическую теорему о равном распределении энергии по степеням свободы. ТЕОРИЯ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ ЭЙНШТЕЙНАТеория Эйнштейна также как классическая теория рассматривает кристалл как совокупность N зависимых частиц, колеблющихся с одной частотой. Однако колеблющаяся частица уподобляется квантовому осцилятору. Средняя энергия его определяется формулой Планка: E(в)=hν/ (e(c.hν/kT)-1) Для частицы с 3-мя степенями свободы при счете на 1 грамм атома, средняя внутренняя энергия E(в)=3N*(hν(в)/ [e(c.hν/k) – 1]). Этой выражение преобразуем: E(в)=3Nk*[(hν/k) / (e(c.hν/k)-1)]; hν/k=θ – характеристическая температура Дебая. => θ определяется частотой колебаний и является постоянной для данного вещества. E(в)=3R*[θ / (e(c.θ/T)-1)]; C=dE(в)/dT=3R*[(θ/T)(c.2)*e(c.θ/T) / (e(c.θ/T)-1)(c.2)]. Возможны случаи: 1] T<<θ, T0, тогда e(c.θ/T)>>1 => (e(c.θ/T)-1)(c.2)≈(e(c.θ/T)(c.2)); C=3R*(θ/T)(c.2)*e(c.-θ/T); (θ/T)(c.2)∞; e(c.-θ/T)0; lim(T0)C=0. 2] T>>θ, T∞; (θ/T)/(e(c.θ/T)-1)=1 – ½ θ/T + (1/6)*(θ/T)*(1/2!) - …=1 lim(T∞)C=3R. Качественные выводы теории Эйнштейна хороши, но попытка количественно расчитать теплоемкость при низких температурах приводит к расхождению с опытными данными, что обусловлено основным допущением: независимостью колебаний частиц в узлах кристаллической решетки и постоянством частоты этих колебаний. | 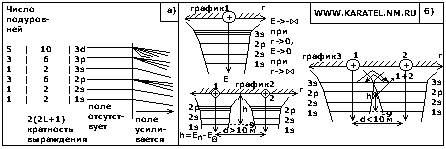 Частицы в кристалле тесно связаны между собой, поэтому тепловые колебания частиц в узлах кристаллической решетки нельзя рассматривать как простые синусоидальные колебания. Они являются сложными, однако, любое сложное колебание можно разложить в ряд Фурье на ряд простых синусоидальных колебаний. Каждое такое простое синусоидальное колебания является независимым от других и называется “модой” или нормальным колебанием. Мода может быть уподоблена квантовому осцилятору, энергия которого определяется колебательным и квантовым числом. E=(V+1/2)h(в)ω, V=0,1,2,3,4… При V=0, Eo= ½ h(в)ω. Т.о. в кристалле мы имеем совокупность мод. В силу взаимозависимости тепловых колебаний в кристалле можно говорить об аналогии между распространением тепловых волн в среде. Т.к. согласно принятой модели кристалла, колебания в узле кристаллической решетки передаются соседней частице, связанной с частицей этого узла, и т.д. Можно говорить о распространении в кристалле тепловых упругих волн. Энергия нормальных колебаний не может произвольные значения. Согласно уравнению Шреддингера она меняется дискретными порциями, кратными h(в)ω. Минимальная порция энергии, которой может обладать нормальное колебание в узле кристаллической ячейки, называется фононом. Т.о. фонон – это тепловой квант. Фонон обладает энергией h(в)ω или h(в)ν. Обладая энергией, он обладает массой и импульсом. Т.о. в кристалле мы имеем совокупность фононов. Теория теплоемкости твердых тел Дебая исходит из: 1) кристалл можно заменить совокупностью фононов, причем концентрация фононов в кристалле и их подвижность таковы, что можно проводить аналогию между совокупностью фононов в кристалле и молекулярным газом. Для обозначения совокупности фононов в кристалле вводится понятие фононный газ. 2) Следует различать фононный и молекулярный газ. Структурными частицами и носителями движения в молекулярном газе являются частицы, из которых состоит газ. Фононы же являются только носителями движения. Т.к. частицы в узлах кристаллической решетки не могут поступательно перемещаться. 3) расчет средней энергии фонона при назких температурах Дебая показал, что E(в)(инд.ф)(при T0)aT(c.4). Поэтому теплоемкость в области низких температур, согласно Дебаю: C=dEвн/dTpT(c.3) – закон кубов Дебая (T0). |
