 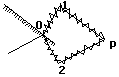      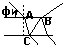           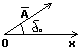 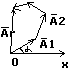 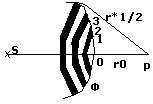  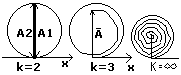    λ=0,4 мкм – видимый оптический диапозон. В настоящее время под оптич. диапозоном понимается диапозон λ=(1*10(c. -9))см. Осн. вопрос оптики – вопрос о природе света. Законы геометрической оптики: закон прямолинейного распространения, закон независимости световых лучей, законы отражения и преломления света. λ=0,4 мкм – видимый оптический диапозон. В настоящее время под оптич. диапозоном понимается диапозон λ=(1*10(c. -9))см. Осн. вопрос оптики – вопрос о природе света. Законы геометрической оптики: закон прямолинейного распространения, закон независимости световых лучей, законы отражения и преломления света.
ИНТЕРФЕРЕНЦИЯ СВЕТА
СВЕТОВАЯ ВОЛНА
Согласно теории Максвела волна распространяется с фазовой скоростью v=c / √εμ`; ε, μ – диэлектрическая и магнитная проницаемости сред, в воздухе ≈1. v=c/ √ε`; c/v=n, n=√ε`. Для электро-магнитной волны распр. вдоль оси х: E(в)=Eo cos (ωt – kx + φ);
H(в)=Ho cos (ωt – kx + φ); k=π/λ – волновой вектор/
волновое число. E,H – векторы напряженности.
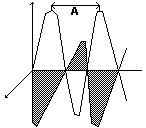
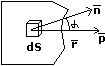
Eo, Ho – их амплитуды. Моментальный снимок
эл-маг волны можно изобразить в виде ----------
Векторы E и H – колеблются. В перпендикулярной
плоскости, значение эл-маг волны поперечны. Опыт
показывает, что электро-хим., физио-логич., фото-хим.
и др. действия обусловлены колебанием вектора E. В дальнейшем будем говорить о световом векторе, подразумевая под ним колебание вектора напряженности электрического поля E. Обозначим амплитуду светового вектора через A. Закон, по которому меняется во времени и пространстве амплитуда светового вектора называется уравнением световой волны: y=Acos(ωt-kx+φ); y=Acos(ωt+φ); Световая волна несет с собой энергию. Плотность потока этой энергии определяется вектором Пойнтинга
S(в)=[E(в)*H(в)]. Согласно электро-магнитной теории Максвела амплитуды E и H связаны: Eo√ε0ε`=Ho√μ0`; H=Eo√ε` *√ε0/μ0` = Eo n √ε0/μ0`; HnEo; S(в)Ho Eo nEo(c.2); Среднее значение S(в) – интенсивность световой волны: InEo(c.2)nA(c.2); InA(c.2)
ПОНЯТИЕ О КОГЕРЕНТНОСТИ
Под когерентным понимается согласованное протекание во времени и пространстве 2х или более колебательных или волновых процессов. Принцип суперпозиции световых полей. Световой вектор складывается с другим без искажений. Пусть в данную точку пространства приходят 2 световые волны, одной частоты, световые векторы которых колеблются в одной плоскости: y1=A1cos(ωt+φ1); y2=A2cos(ωt+φ2); Результирующая волна запишется в виде: y=Acos(ωt+φ); Амплитуда результирующих колебаний: A=A1(c.2)+A2(c.2)+2A1A2cos(φ2-φ1); A(c.2)≠ A1(c.2)+A2(c.2); I≠ I1+I2; Результ. слож. зависит от разности фаз δ=φ1-φ2 и заключается в пределах: |A1-A2|<=A<=|A1+A2|; δ=+ - (2k+1)π; δ=+ - 2kπ, k=0,1,2… Колебания затухающие, обрываются и возникают с измененной фазой. Прибор, который фиксирует интенсивность, регистрирует не мгновенное значение интенсивности, а усредненное по времени значение. Чтобы его найти: I(в)=A(в)(c.2)=(1/τ)*∫[0 – τ] A(c.2) dτ=A1(c.2)+A2(c.2)+
+2A1A2*(1/τ)*∫[0 – τ] cosδdτ; 2 случая: 1) δ=φ2-φ1≠const;
(1/τ)*∫[0-τ]cosδdτ=0; I(в)=A(c.2)=A1(c.2)+A2(c.2); I(в)=I1(c.2)+I2(c.2);
2) δ=φ2-φ1=const; (1/τ)*∫[0-τ] cosδdτ=cosδ; I(в)=A(в)(c.2)=A1(c.2)+
+A2(c.2)+2A1A2cosδ; I(в)≠I1+I2; Это мы получим в предположении, что налагаются 2 волны одинаковой частоты. Рез. сложение 2х волн при котором не происходит простое суммирование – это интерференция. В тех точках пространства, в которых 2 волны удовлетворяют соотн. cosδ>0, I>I1+I2 (наблюдается интерфериционный максимум). А там, где cosδ<0 наблюдается ослабление света или интерференционный минимум. Если I1=I2, то там, где cosδ>0, будет I(в)=I1+I2+I3+I2, а где I(в)=I1+I1-2I1≈0 если I(в)=I1+I1=2I2. ИНТЕРФЕРЕНЦИЕЙ света называется наложение 2х или более волн, в результате которого происходит перераспределение светового потока пространства. В одних точках пространства происходит усиление света – интерфериционный максимум, в других – ослабление, возникает минимум. Интерферировать могут только когерентные волны. Критерий когерентности: 1) ω(f)=const – волны монохромны, 2) δ=φ2-φ1=const, φ2=φ1, δ=0, 3) световые векторы должны колебаться в одной плоскости, т.е. E1(в)||E2(в). Понятие когерентности является относительным. Для характеристики когерентности вводят понятие пространственной и временной когерентности. Временем когерентности называют такой промежуток времени, в течении которого случайное изменение фазы волны достигает значения π. tког*c=lког – длина когерентности – отрезок, проход. волной, на длине которого случайное изменение фазы волны приобретает знанчение π.
СПОСОБЫ ПОЛУЧЕНИЯ КОГЕРЕНТНЫХ ИСТОЧНИКОВ
Естественные излучатели не когерентны и излучают некогерентные волны. Причина их некогерентности заключается в самом механизме излучения. t=10(c.- 8) c. – время жизни возбужденного состояния атома. Цуг – излучение по истечении этого времени, которое испускает атом. ∆х=cτ=
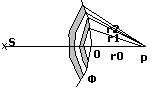
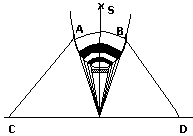
=3*10(c.8)*10(c. – 8)=3м. Принцип получения когерентных волн от естественных излучателей: ПРИНЦИП ФРЕНЕЛЯ: волну, испускаемую отдельными атомами светящегося тела раздел. на 2 путем разложения, преломления, затем обе половинки волны заст. пройти различные пути в пространстве и налог. друг на друга.
В точке 0 – одинаковые фазы, в точку p они придут
с разными фазами, т.к. проходят различные пути в
пространстве. Практический способ: бипризмы
Френеля, Щели Юнга, зеркало Ллойда.
РАСЧЕТ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ ОТ 2Х КОГЕРЕНТНЫХ ИСТОЧНИКОВ
Пусть в точке 0 осуществляется принцип Френеля, т.е.
раздвоение волны, в т. р находится наблюдатель.
Уравнение падающей в точку 0 волны: y=Acosωt
1 проходит путь: OAP=L1; n1; OBP=L2; n2
В точке p обе половинки приходят с разными фазами и
1-я волна возб. в точке p колебания: y1=Acosω(t- L1/v1),
а вторая волна: y2=Acosω(t- L2/v2); v1,v2 – фазовые скорости волн,
v1=c/n1, v2=c/n2. Разность фаз δ=φ1-φ2=ω(t- L1/v1) – ω(t- L2/v2)=
=ω(L2n2 – L1n1)=(2ω/c)*(L2n2 – L1n1)=(2π/λo)*(L2n2 – L1n1);
L*n=S – оптическая длина пути. L2n2 – L1n1=S1 – S2 = ∆ - оптическая разность ходов, δ=2π∆/λo => если на оптическую разность хода ∆=+-kλo=
=+- 2k*(λi/2), k=0,1,2…, δ=+ - (2π/λo)*kλo=+ - 2kπ. Волны приходят в одинаковых фазах и их амплитуда
складывается. Это условие
интерференционного максимума.
Если ∆=+ - (2k+1)*(λo/2), то
δ=+ - (2π/λo)*(2k+1)*(λo/2)=+ - (2k+1)π
Волны, приходят в противофазе, т.е.
они антифазны и при наложении в т. р,
их амплитуда будет вычитаться.
Значит это условие интерференционного
минимума. Применим это условие при
расчете интерференционной картины
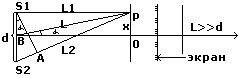
от 2х когерентных источников. Два
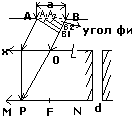
когерентных источника S1 и S2,
расстояние между ними d:
Опред. рез. наложения волн в
точке р: ∆/d=x/L, т.к. L>>d, то
BP≈L, тогда ∆=dx/L.
Если ∆Єz, то в точке светлая
полоса, x=L∆/d; ∆x=Lλ/d –
ширина темной полосы.
Для монохромных волн
max расх. ∆=0, ∆φ=0,
кроме max центральн.
ИНТЕРФЕРЕНЦИЯ В ТОНКИХ СЛОЯХ
При падении света на тонкую пластинку происходит отражение
света от верхней и нижней поверхности пластинки, обе волны
когерентны и могут интерферировать. Пусть пучок волн
падает параллельно на плоско-параллельную пластинку.
Любая волна, попадающая в точку А частично отражается,
частично преломляется, на нижней поверхности в точке С частично преломляется возд., отражается. Для определения разности хода между 1 и 2 волнами – плоск. BD – проекц. волн. фронта волны на чертеж. После плоскости BD волны идут без изменения разности хода. 1 волна проходит AD в возд., 2 волна за это же время AC+CB следует учесть, что в точке А 1-я волна отражается от оптической плотности среды в менее плотн. Фаза повор. на π, => 1 волна проходит путь в полволны. Между 1 и 2 волнами есть дополнительная разность хода: ∆=2d√φ(c.2) – x(c.2)`=+ - λ/2;
∆=2dcosφ + - λ/2. Если пластинки освещается монохромным светом, то при наблюдении отраженного света глазом аккомандир. на бескон., пластинка будет светлой, если: ∆= + - kλ; ∆=+ - (2k+1)*(λ/2); условие max:
2d√n(c.2) – sin(c.2)φ` + - λ/2=+ - kλ; условие минимума:
2d√n(c.2) – sin(c.2)i` + - λ/2=+ - (2k+1) λ/2
|
УСЛОВИЕ НАБЛЮДЕНИЯ ЧЕТКОЙ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ
Если свет не монохроматический, а представляет собой некоторый спектр волн, то при данном угле падения условие max: ∆=ki λi (kλ1=(k+1)λ2=
=(k+2)λ3=…). Чтобы такое наблюдение оказалось возможным, необходимо, чтобы интервал длин волн был ограничен λЄ[λ; λ+∆λ]. k(λ+∆λ)=(k+1)λ;
∆λ=λ/2; Чем больше d, тем больше k, и тем теснее располагаются полосы.
1Å=10(c.-10)м – анстрем. ∆λ=100Å, λ=5000Å, k=50. Используя соотношение (1) получим n=1,5; d=8мкм, ∆λ=0,1Å, d>в 10(c.3). Интерференцию можно наблюдать в клинообразных тонких слоях при этом угол схождения поверхностей должен быть от нескольких секунд до минут.
ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ И РАВНОГО НАКЛОНА
Оптическая разность хода – функция нескольких величин ∆=f(d, λ, n, i). Если все эти величины меняются одновременно, то четкой интерфериционной картины не наблюдается, наблюдать четкую интерфериционную картину можно тогда, если все величины, кроме одной, постоянны. С практической
точки зрения интересны 2
случая:
1) монохроматическая
волна падает на
плоско-параллельный
изотропный слой. В этом
случае d, λ, n=const, ∆=f(i).
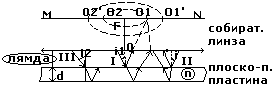
Поскольку волны падают на плоско-параллельную пластину под разными углами, образуют конус, то в следствии интерференции этих волн на экране они соберутся в виде окружности диаметром 0102 (светлой), если выполняются условия ∆1=f(i1)=+ - kλ. С диаметром 01’02’, если ∆2=f(i2)=
=+ - k2λ, ∆1≠∆2, k1≠k2, i2>i1. Поскольку в этом случае
интерферируют волны, падающие на пластинку под
одинаковыми углами, то интерферентные полосы называются
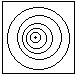
полосами равного наклона. Они представляют собой светлые
кольца, разделенные темными промежутками, отвечающие min,
и локализованные в бесконечность.
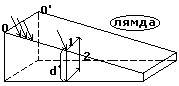
2) Пучок монохроматических волн падает
параллельно на изотропный слой
переменной толщины. λ, n, i=const, ∆=f(d).
Волны 1 и 2 будут интерферировать, если
выполняется условие ∆1=f(x1)=+ - k1λ (1).
Для всех точек, соответствующих толщине
d1, будет выполняться условие (1) и вблизи
поверхности клина образуется интерфериционная полоса, параллельная ребру клина. Во 2 случае ∆2=f(d2)=+ - k2λ (2). В этом случае интерферируют волны, приходящие на поверхность клина в точки, соответствующие ребру клина и приходящиеся на одинаковую толщину. Поэтому наблюдаемые полосы называются полосами равной толщины. Они локализуются вблизи поверхности клина и представляют собой совокупность темных и светлых полос.
МНОГОЛУЧЕВАЯ ИНТЕРФЕРЕНЦИЯ
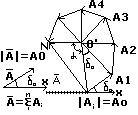
Наблюдать интерференцию многих волн можно с посощью специальных преспособлений: этакое Фабри-перо или дифракционная решетка. В случае интерференции N плоских волн в точках с max интерференции результирующая амплитуда A=Nai, Jmax=N(c.2)Ai(c.2)=N(c.2)Ji(c.2). Суммарная интенсивность будет равна сумме интенсивностей всех волн Jсум=N*J. По закону сохранения энергии с увеличением N, max должны, в силу возрастания их яркости, сужаться и должны увеличиваться области с минимальной освещенностью. Предположим, что имеем N плоских волн одинаковой амплитуды A, направленных в одну сторону, при этом разность фаз между i+1 и i волной не зависит от i=0,1,2,3 и
равна δ=δ0. Найдем результирующую амплитуду
при интерференции N плоских когерентных волн.
Это удобно производит с помощью графического
метода сложения амплитуд, основанного на понятии
вращающегося вектора амплитуды. Под вектором
амплитуды понимают вектор, длинна которого равна
амплитуде колебания, а угол, который этот вектор
образует с произвольно выбранной осью отсчета,
равен начальной фазе.
A=2*00’|sina/2|; x=2π – N δ0; 00’=Ao/(2|sinδo/2|);
A=[Ao sin|π – (N δo / 2)| ]/ |sinδo/2|; J=A(c.2)=Jo*(sin(c.2)(π – N δo) / sin(δo/2)) (1). Формулу (1) мы получили из предположения, что δo=0;+ - π; + - 2π;
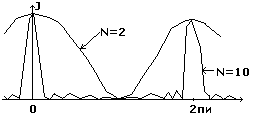
+ - 2π и т.д. Из формулы (1) следует, что δo(max)=+ - 0; + - 2π; + - 4π и т.д. Т.о. условие δo=+ - 2k π – max, которые называются главными. Если векторы Ai и Ai+1 направлены в противоположные стороны, то δo=0, и тогда A результирующее при N – четном, N=2k, A=0, а при N=(2k+1), A=Ao. из формулы (1) можно расчитать ширину главного интерфериционного максимума. Нулевой max (k=0) имеет место при δo=0. Из формулы (1) => что ближайший к нулевому max-м минимум должен удовлетворять условию: N δo’ / 2 = + - π; => ширина главного max на экране ∆x=4π/N; Т.о. ширина главного max обратно
пропорциональна числу интерферирующих
волн и по мере увеличения N уменьшается.
Min на экране будет тогда, когда
Nδo/2=+ - 2π; 3π… δo=+ - 2k π / N – min.
Между 2 соседними минимумами должны
находиться добавочные max.
ПРИМЕНЕНИЕ ИНТЕРФЕРЕНЦИИ
Интерференция применяется в сверхточных претензионных измерениях. Используются приборы – интерферометры, в их основе лежит явление интерференции. 2-ая область – контроль за чистотой обработки поверхности высокого класса точности. 3) для определения коэффициента линейности расширения твердого тела – делатометр. 4) просветление оптики.
ДИФРАКЦИЯ СВЕТА
Дифракцией света называется явление отклонения от прямолинейного распространения волн, огибание волнами препятствий и захождение волн в область геометрической тени.
ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ
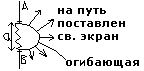
Качественно явление дифракции света объясняется на основе принципа Гюйгенса: каждая точка пространства до которой дошло световое возбуждение становится источником вторичных волн, распространяющихся в данной среде с характерной для нее фазовой скоростью v. Геометрическоее место точек, до которого доходит световое возбуждение за один и тот же промежуоток времени носит название фронта волны или волновой поверхности. Огибающая вторичных волн –
есть положение волнового фронта в последующий
момент времени. Пусть расространяется волна и ее
волновой фронт в некоторый момент времени есть
поверхность Ф. Такое распространение показывает,
что волновой фронт загибается на концах, также как и лучи (нормаль к волновой поверхности). Количественный расчет дифракционного явления был предпринят: Френелем, который исходил из ряда положений, принимающихся без доказательства и составляющих принцип Гюйгенса-Френеля. Эти положения сводятся к следующему: 1) следуя
Гюйгенсу Френель предложил заменить реально
действующий источник излучения эквивалентной ему
совокупностью вторичных (виртуальных) источников и
испускаемых ими торичных волн. 1) В качестве вторичного
источника выступают бесконечно малые участки
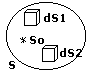
поверхности S замкнутой вокруг So. Выбор поверхности S произволен, но чаще всего поверхность S совпадает с нулевой поверхностью. 2) согласно Френелю все вториные источники когерентны между собой и испускают когерентные волны, в любой точке вне S, волны, идущие от So представляют собой интерференцию вторичных волн. Для поверхности S совпадающей с волновым фронтом все вторичные испускаемые колебания в одной фазе. 3) для поверхности S, совпадающей с волновой поверхностью разные по площади вторичные источники испускают равное по мощности вторичное излучение. dS1=dS2=dSn; dP1=dP2=dPn (P-мощность).
4) Каждый вторичный источник, излучает направление нормали к волновой поверхности в данной точке. Интенсивность излучения
(амплитуда) в точке p тем меньше, чем больше угол α
между внешней нормалью и радиус-вектором проведенным
в точке наблюдения. Фаза результирующего колебания
зависит тоже от r (в). 5) если чсть волновой поверхности перекрыто непразрачным экраном, то световое воздействие в точке наблюдателя осуществляется открытыми вторичными источниками. Для нахождения результирующего колебания в точке P, необходимо просуммировать вторичные источники по их амплитуде и фазам. Существует приближенный метод расчета интерференции вторичных волн – метод зон Френеля
| МЕТОД ЗОН ФРЕНЕЛЯ
Пусть в точке S находится точечный источник
ионохроматического света, который по всем
направлениям испускает сферичные волны.
В любой момент времени волновая поверхность
- есть сферичная поверхность S. В точке P
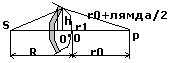
находится наблюдатель. Для определения светового воздействия в точке P согласно принципу Г-Ф следует заменить реальный волновой фронт эквивалентной совокупностью вторичных источников. В методе зон Френеля в качестве вторичного источника выступают кольцевые зоны получившиеся на поверхности Ф путем проведения с центром в точке P окружности с радиусом r1=r0+λ/2; r2=r1+λ/2=r0+2λ/2; r3=r2+λ/2; rk=r0+kλ/2.
=> колебания от каждой последующей зоны сдвинуто по отношению к колебанию от предыдущей зоны на λ/2, т.е. находятся в противофазе и будут гасить друг друга, т.е. их
амплитуды будут вычитаться.
Ap=A1-A2+A3-A4+…+Ak; Можно
доказать, что все зоны имеют
одинаковую площадь:
δ=2πkx; r1(c.2)=R(c.2) – (R-x)(c.2); r1(c.2)=(r0+λ/2)(c.2) – (r0 + x)(c.2);
R(c.2) – R(c.2)+2kx – x(c.2)=r 0(c.2)+r 0λ+(λ/4) – r 0(c.2) – 2r x; 2Rx=
=Roλ-2 r 0 x; 2x(r 0 +R)=r 0 λ; x=(r 0 λ)/2(r 0 +R); λ=10(c. –7) – можно пренебречь. δ1=2πkx=π*(R r 0 / (r+R))λ – площадь первой зоны. δ2’ – площадь шарового сектора, δ2’=2π*(2r 0 / (r 0 +R))λ. δ2 – площадь второй зоны. δ2=δ2’-δ1=π*(R r 0 / (r 0 +R))λ; δ1=δ2=…=δk, к – число волн.
r1(c.2)=R(c.2) – (R-x)(c.2); r1(c.2)=R(c.2) – R(c.2) + 2kx – x(c.2); x – пренебрегаем. r1=√R r 0 λ / (R+r 0)`; rk=√R r 0 k λ/ (R+r 0)` - радиус любой зоны для сферического волнового фронта. Т.к. площадь всех зон одинакова, то все зоны испускают одинаковое по мощности вторичное излучение. До наблюдателя излучения доходят от разлиной интенсивности, т.к. различным является угол α между внешней нормалью и радиус-ветором от зоны до точки наблюдения. Поскольку r1A2>A3…>Ak,
Ap=A1-A2+A3-A4+…+Ak. Это выражение можно представить в виде:
Ap=(A1/2) + ((A1/2) – A2 + (A3/2)) + ((A3/2) – A4 +(A5/2))…+ - Ak/2;
(A1+A3)/2=A2, (A3+A5)/2=A4; амплитуда зоны равна полусумме амплитуд соседних зон. Ap=(A1/2) + - (Ak/2). Если k0 полностью открывается волновой фронт, то Ak/20, и Ap=A1/2. В итоге при полностью открытом волновом фронте свет распространяется как бы вдоль узкого канала, соизмеримого с центральной зоной Френеля, т.е. прямолинейна.
ГРАФИЧЕСКИЙ МЕТОД НАХОЖДЕНИЯ РЕЗУЛЬТИРУЮЩЕЙ АМПЛИТУДЫ
В основе метожа лежит понятие о векторе амплитуды.
Если в данною точку приходит амплитуда, выражение
нескольких векторов Ai, то Ap(в)=Σ[i=1- k] Ai.
Если в данную точку приходит световое возбуждение от
части волнового фронта, то эту часть разбивают на малые
участки, столь малые, чтобы можно было считать, что фаза
колебаний, создаваемых в точке наблюдения – есть величина
const. Тогда действ. r-го участка выр. A1, 2-го A2.
Применим графический метод к методу зон Френеля:
Разобьем центральную зону на 6 участков.
A1(в) – выраж. действ. в
точке P всей 1-ой зоны
Френеля. Если участки
уменьшаются до малых
размеров, то ломанная
линия заменится дугой,
близкой к полу-окружности.
A2(в) – направленный в противоположную
сторону A1(в), символизирует вывод метода
зон Френеля о противоп. разности фаз колебаний относительно зон Френеля. A∞≈A1/2. По своему характеру все дифракционные явления делятся на 2 класса: 1) дифракционная картина локализуется на конечном растоянии от преград и препятствий. Эти явления носят названия – дифракции Френеля. 2) Отн. явл., в котором дифракционная картина локализуется на бесконечности => дифрагируют плоские волны от удаленных источников, эти дифракционные явления носят название дифракции Фраингофера.
ДИФРАКЦИЯ ФРЕНЕЛЯ НА КРУГЛЫХ ОТВЕРСТИЯХ
а) CD – экран. Экран с круглым отверстием
AB. Исследуем световое воздействие в
точке р, лежащей на линии пересечения
источника S с центром отр. Отверстие
вырезает часть волновой поверхности.
Разобьем открытую часть волновой поверхности на зоны Френеля. В зависимости от размеров отверстий на ней укладывается то или иное количество зон. Если отверстие пропускает 1, 3 или 5 зон, то световое воздействие в точке р больше, чем при полностью открытом волновом фронте. Максимум светового воздействия в точке р при k=1 (см последний рисунок в прошлом абзаце). Если отверстие открывает небольшое четное число зон Френеля (k=2,4,6), то световое воздействие всегда больше, чем при полностью открытом волновом фронте. Min воздействия отвечает отверстию в 2 зоны Френеля.
б) Дифракция Френеля на … Световая волна встречает на своем пути непрозрачный круглый экран AB (на рисунке
ошибка – АВ – там снизу на самом деле).
Исследуем световое воздействие в точке p.
Экран перекрывает часть зон Френеля.
Разобьем открытую часть световой
поверхности на зоны Френеля. Согласно
рассуждениям методом зон Френеля:
A=(An+1)/2 + [(An+1)/2 – (An+2)/2 + (An+3)/2]
+ … + - Ak/2. n – число перекрытых зон
Френеля. An+1 – амплитуда от 1-ой открытой
зоны. A=(An+1)/2. Итак, если число зон, перекрытых экраном AB невелико, точка р останется освещенной, причем интенсивность освещенности не отличается практически от интенсивности освещенности, создаваемой полностью открытым световым фронтом. По мере увеличения размеров экрана АВ амплитуда от 1-ой открытой зоны будет убывать, однако точка р остается освещенной до тех пор, пока число перекрытых зон Френеля достаточно мало и лишь при условии, что экран перекрывает большее число зон Френеля, в точке р будет наблюдаться min, т.е. геометрическая тень от экрана АВ.
ЧАСТНЫЕ СЛУЧАИ ДИФРАКЦИИ
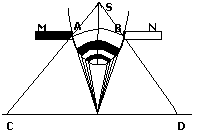
Пусть монохроматическая волна падает
нормально на узкую щель АВ шириной а,
в непрозрачном бесконечном экране. Как
только плоский волновой фронт достигает
плоскости щели. Каждая точка щели
становится источником вторичных волн.
Вторичные волны распространяются вдоль
всех направленияй. Выберем одно, характеризуемое углом φ, угол φ – угол дифракции, т.е. углом между направлением падающей и дифрагируемой волны. Параллельно плости щели – собирательная линза L, в фокальной плоскости. K-ый экран наблюдения MN. После преломления линзы вторичные волны, идущие под углом φ к фронту АВ, соберутся в некоторой точке р экрана, в точке пересечения побочно оптической оси линзы с фокальной плоскостью. В точке р будет наблюдаться результат интерференции вторичных волн, идущих от фронта АВ. Для определения результата интерференции в точке р воспользуемся методом зон Френеля. Для этого опустим нормаль AC на направление дифрагированных под углом φ волновую нормаль. AC есть проекция волнового фронта дефрагированных волн на плоскость чертежа. Нормаль отсекает отрезок CB на малые открезки, равные λ/2, т.е. CB1=B1B2=B2B3=…=λ/2. Проведем через эти малые отрезки прямые, параллельные AC до пересечения с AB. Плоскость АВ оказалась разбитой на участки, причем вторичные колебания, идущие от точки А и А1 имеют разность хода λ/2 => при наложении в точке р их амплитуды гасят друг друга, т.к. колебания находятся в противофазе. Аналогично колебания от точки А1 и точки А2, точки А3 и точки А4 и т.д. гасят друг друга. => отрезки АА1, А1А2, А2А3 и т.д. есть зоны Френеля. Если на плоскости щели АВ уложится четное число зон Френеля, т.е. n=2k, где k=1,2,3 и т.д., то в точке р – min, а это значит, что СВ разбит на четное число отрезков λ/2. ∆=asinφ; asinφ=+ - kλ; (1) – условие дифракционных min. Аналогично можно показать, что условие max соответствует случаю, когда на оптической разности хода нечетное число отрезков λ/2. asinφ=+ - (2k+1)λ/2 – max; Для определения интенсивности в различных точках дифракционной картины на экране, мы можем воспользоваться формулой, определяющей результирующу амплитуду при интерференции многих волн. A=Ao *(|sin(Nδo/2)| / sin(δo/2)). Амплитуды вторичных волн малы, и разность фаз меняется в пределах разности хода ∆=asinφ. Суммарная разность фаз колебаний их, идущих от точки А и точки В.
|
 Скачать 1.6 Mb.
Скачать 1.6 Mb.