мат мод хищник жертва. Исследование элементарной модели хищникжертва
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
Содержание Введение 1. Параметры и основное уравнение модели хищник-жертва 2. Качественное исследование элементарной модели «хищник-жертва» 2.1 модель трофического взаимодействия по типу «хищник-жертва» 2.2 обобщённые модели вольтера типа «хищник-жертва» 3. Практическое применение модеели «хищник-жертва» 4.Модели взаимодействия двух видов 4.1Гипотезы Вольтерра 4.2Аналогии с химической кинетикой. 4.3Вольтерровские модели взаимодействий 4.4 Классификация типов взаимодействий Конкуренция. 4.5Хищник-жертва. 4.6Обобщенные модели взаимодействия видов 4.7Модель Колмогорова. 4.8Модель взаимодействия двух видов насекомых Макартура. 4.9Модель А.Д.Базыкина 6. Система ХИЩНИК+ЖЕРТВА 7. МОДЕЛЬ «ХИЩНИК - ЖЕРТВА» И МАКРОЭКОНОМИЧЕСКАЯ МОДЕЛЬ ГУДВИНА 8. лИТЕРАТУРА Введение В настоящее время задачи экологии имеют первостепенное значение. Важным этапом решения этих задач является разработка математических моделей экологических систем. Одной из основных задач экологии па современном этапе является изучение структуры и функционирования природных систем, поиск общих закономерностей. Большое влияние на экологию оказала математика, способствующая становлению математической экологии, особенно такие её разделы, как теория дифференциальных уравнений, теория устойчивости и теория оптимального управления. Одной из первых работ в области математической экологии была работа А.Д. Лотки (1880 - 1949), который первый описал взаимодействие различных популяций, связанных отношениями хищник - жертва. Большой вклад в исследование модели хищник -жертва внесли В. Вольтерра (1860 - 1940), В.А. Костицин (1883-1963) В настоящее время уравнения описывающие взаимодействие популяций, называются уравнениями Лотки - Вольтерра. Уравнения Лотки - Вольтерра описывают динамику средних величин - численности популяции. В настоящее время на их основе построены более общие модели взаимодействия популяций, описываемые интегро-дифференциальными уравнениями, исследуются управляемые модели хищник - жертва. Одной из важных проблем математической экологии является проблема устойчивости экосистем, управления этими системами. Управление может осуществляться с целью перевода системы из одного устойчивого состояния в другое, с целью её использования или восстановления. 1. ПАРАМЕТРЫ И ОСНОВНОЕ УРАВНЕНИЕ МОДЕЛИ ХИЩНИК-ЖЕРТВА Попытки математического моделирования динамики как отдельных биологических популяций, так и сообществ, включающих взаимодействующие популяции различных видов, предпринимались давно. Одна из первых моделей роста изолированной популяции (2.1) была предложена еще в 1798 г. Томасом Мальтусом: Данная модель задается следующими параметрами: N - численность популяции; Разность между коэффициентами рождаемости и смертности. Интегрируя это уравнение получаем: где N(0) – численность популяции в момент t = 0. Очевидно, что модель Мальтуса при > 0 дает бесконечный рост численности, что никогда не наблюдается в природных популяциях, где ресурсы, обеспечивающие этот рост, всегда ограничены. Изменения численности популяций растительного и животного мира нельзя описывать простым законом Мальтуса, на динамику роста влияют многие взаимосвязанные причины – в частности, размножение каждого вида саморегулируется и видоизменяется так, чтобы этот вид сохранялся в процессе эволюции. Математическим описанием этих закономерностей занимается математическая экология – наука об отношениях растительных и животных организмов и образуемых ими сообществ между собой и с окружающей средой. Наиболее серьезное исследование моделей биологических сообществ, включающих в себя несколько популяций различных видов, было проведено итальянским математиком Вито Вольтерра: 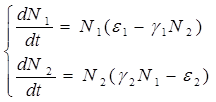 , ,где - численность популяции; Коэффициенты естественного прироста (или смертности) популяции; - коэффициенты межвидового взаимодействия. В зависимости от выбора коэффициентов модель описывает либо борьбу видов за общий ресурс, либо взаимодействие типа хищник - жертва, когда один вид является пищей для другого. Если в работах других авторов основное внимание уделялось построению различных моделей, то В. Вольтерра провел глубокое исследование построенных моделей биологических сообществ. Именно с книги В. Вольтерра, по мнению многих ученых, началась современная математическая экология. 2. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ЭЛЕМЕНТАРНОЙ МОДЕЛИ «ХИЩНИК-ЖЕРТВА» 2.1 Модель трофического взаимодействия по типу «хищник-жертва» Рассмотрим модель трофического взаимодействия по типу «хищник-жертва», построенную В. Вольтерром. Пусть имеется система, состоящая из двух видов, из которых один поедает другой. Рассмотрим случай, когда один из видов является хищником, а другой - жертвой, и будем считать, что хищник питается только жертвой. Примем следующую простую гипотезу: Коэффициент прироста жертвы; Коэффициент прироста хищника; Численность популяции жертвы; Численность популяции хищника; Коэффициент естественного прироста жертвы; Скорость потребления жертвы хищником; Коэффициент смертности хищника в отсутствие жертвы; Коэффициент «переработки» хищником биомассы жертвы в собственную биомассу. Тогда динамика численности популяций в системе хищник - жертва будет описываться системой дифференциальных уравнений (2.1): 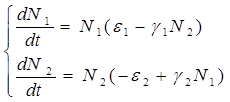 (2.1) (2.1)где все коэффициенты положительные и постоянные. Модель имеет равновесное решение (2.2): По модели (2.1) доля хищников в общей массе животных выражается формулой (2.3): 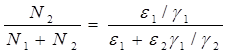 (2.3) (2.3)Анализ устойчивости состояния равновесия по отношению к малым возмущениям показал, что особая точка (2.2) является «нейтрально» устойчивой (типа «центр»), т. е. любые отклонения от равновесия не затухают, но переводят систему в колебательный режим с амплитудой, зависящей от величины возмущения. Траектории системы на фазовой плоскости имеют вид замкнутых кривых, расположенных на различных расстояниях от точки равновесия (рис. 1). 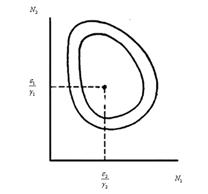 Рис. 1 – Фазовый «портрет» классической вольтерровой системы «хищник-жертва» Разделив первое уравнение системы (2.1) на второе, получим дифференциальное уравнение (2.4) для кривой на фазовой плоскости . 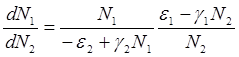 (2.4) (2.4)Интегрируя данное уравнение получим: где - постоянная интегрирования, где 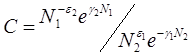 Несложно показать, что движение точки по фазовой плоскости будет происходить только в одну сторону. Для этого удобно сделать замену функций и , перенеся начало координат на плоскости в стационарную точку (2.2) и введя затем полярные координаты: 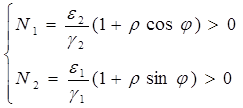 (2.6) (2.6)В таком случае, подставив значения системы (2.6) в систему (2.1), будем иметь: 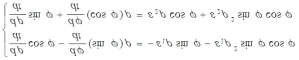 (2.7) (2.7)Умножив первое уравнение на , а второе - на и сложив их, получим: После аналогичных алгебраических преобразований получим уравнение для : Величина , как видно из (4.9), всегда больше нуля. Таким образом, не меняет знака, и вращение все время идет в одну сторону. Интегрируя (2.9) найдем период: Когда мало, то уравнения (2.8) и (2.9) переходят в уравнения эллипса. Период обращения в этом случае равен: 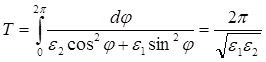 (2.11) (2.11)Исходя из периодичности решений уравнений (2.1), можно получить некоторые следствия. Представим для этого (2.1) в виде: 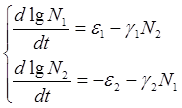 (2.12) (2.12)и проинтегрируем по периоду: 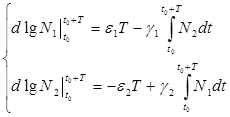 (2.13) (2.13)Так как подстановки от и в силу периодичности обращаются в нуль, средние по периоду оказываются равными стационарным состояниям (2.14): 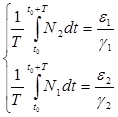 (2.14) (2.14)Простейшие уравнения модели «хищник-жертва» (2.1) обладают рядом существенных недостатков. Так, в них предполагается неограниченность пищевых ресурсов для жертвы и неограниченный рост хищника, что противоречит экспериментальным данным. Кроме того, как видно из рис. 1, ни одна из фазовых кривых не выделена с точки зрения устойчивости. При наличии даже небольших возмущающих воздействий траектория системы будет все дальше уходить от положения равновесия, амплитуда колебаний расти, и система достаточно быстро разрушится. Несмотря на недостатки модели (2.1), представления о принципиально колебательном характере динамики системы «хищник- жертва» получили широкое распространение в экологии. Взаимодействиями «хищник-жертва» объясняли такие явления, как колебания численности хищных и мирных животных в промысловых зонах, колебания в популяциях рыб, насекомых и т. д. На самом деле колебания численности могут быть обусловлены и другими причинами. Предположим, что в системе хищник - жертва происходит искусственное уничтожение особей обоих видов, и рассмотрим вопрос о том, каким образом уничтожение особей влияет на средние значения их численности, если осуществляется пропорционально этой численности с коэффициентами пропорциональности и соответственно для жертвы и хищника. С учетом сделанных предположений систему уравнений (2.1) перепишем в виде: 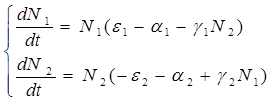 (2.15) (2.15)Предположим, что , т. е. коэффициент истребления жертвы меньше коэффициента ее естественного прироста. В этом случае также будут наблюдаться периодические колебания численности. Вычислим средние значения численностей: 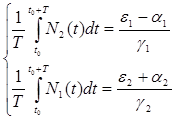 (2.16) (2.16)Таким образом, если , то средняя численность популяций жертвы возрастает, а хищника - убывает. Рассмотрим случай, когда коэффициент истребления жертвы больше коэффициента ее естественного прироста, т. Е . В этом случае Начиная с некоторого момента времени t, при котором , решение второго уравнения (2.15) также начинает убывать и при стремится к нулю. Таким образом, в случае оба вида исчезают. 2.1 Обобщенные модели Вольтера типа «хищник-жертва» Первые модели В. Вольтерра, естественно, не могли отражать все стороны взаимодействия в системе хищник - жертва, поскольку они были в значительной мере упрощены относительно реальных условий. Например, если численность хищника равна нулю, то из уравнений (1.4) следует, что численность жертвы неограниченно возрастает, что не соответствует действительности. Однако ценность этих моделей состоит именно в том, что они были основой, на которой быстрыми темпами начала развиваться математическая экология. Появилось большое число исследований различных модификаций системы хищник - жертва, где были построены более общие модели, учитывающие в той или иной степени реальную ситуацию в природе. В 1936 г. А.Н. Колмогоров предложил использовать для описания динамики системы хищник - жертва следующую систему уравнении: 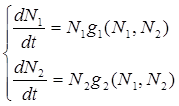 , (2.17) , (2.17)где убывает с возрастанием численности хищников, а возрастает с увеличением численности жертвы. Эта система дифференциальных уравнений в силу ее достаточной общности позволяет хорошо учитывать реальное поведение популяций и вместе с тем проводить качественный анализ ее решений. Позднее в своей работе, Колмогоров исследовал подробно менее общую модель: 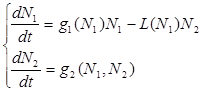 (2.18) (2.18)3. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МОДЕЛИ ХИЩНИК-ЖЕРТВА Рассмотрим математическую модель совместного существования двух биологических видов (популяций) типа "хищник - жертва", называемую моделью Вольтерра - Лотки. Пусть два биологических вида совместно обитают в изолированной среде. Среда стационарна и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов, который будем называть жертвой. Другой вид - хищник также находится в стационарных условиях, но питается лишь особями первого вида. Это могут быть караси и щуки, зайцы и волки, мыши и лисы, микробы и антитела и т. д. Будем для определенности называть их карасями и щуками. Заданы следующие начальные показатели: Со временем число карасей и щук меняется, но так как рыбы в пруду много, то не будем различать 1020 карасей или 1021 и поэтому будем считать и непрерывными функциями времени t. Будем называть пару чисел (,) состоянием модели. Очевидно, что характер изменения состояния (,) определяется значениями параметров. Изменяя параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы во времени. В экосистеме скорость изменения численности каждого вида также будем считать пропорциональной его численности, но только с коэффициентом, который зависит от численности особей другого вида. Так, для карасей этот коэффициент уменьшается с увеличением числа щук, а для щук увеличивается с увеличением числа карасей. Будем считать эту зависимость также линейной. Тогда получим систему из двух дифференциальных уравнений: 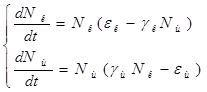 Эта система уравнений и называется моделью Вольтерра-Лотки. Числовые коэффициенты , , - называются параметрами модели. Очевидно, что характер изменения состояния (,) определяется значениями параметров. Изменяя эти параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы. Проинтегрируем оба уравнения систему по t, которое будет изменяться от - начального момента времени, до , где T – период, за который происходят изменения в экосистеме. Пусть в нашем случае период равен 1 году. Тогда система принимает следующий вид: 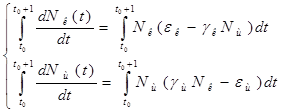 ; ;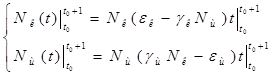 ; ;Принимая = и = приведем подобные слагаемые, получим систему, состоящую из двух уравнений: 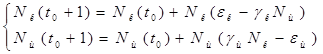 Подставив в полученную систему исходные данные получим популяцию щук и карасей в озере спустя год: 4.Модели взаимодействия двух видов Гипотезы Вольтерра. Аналогии с химической кинетикой. Вольтерровские модели взаимодействий. Классификация типов взаимодействий Конкуренция. Хищник-жертва. Обобщенные модели взаимодействия видов. Модель Колмогорова. Модель взаимодействия двух видов насекомых Макартура. Параметрический и фазовые портреты системы Базыкина. Основателемсовременной математической теории популяций справедливо считается итальянский математик Вито Вольтерра, разработавший математическую теорию биологических сообществ, аппаратом которой служат дифференциальные и интегро-дифференциальные уравнения. (Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris , 1931). В последующие десятилетия популяционная динамика развивалась, в основном, в русле высказанных в этой книге идей. Русский перевод книги Вольтерра вышел в 1976 г. под названием: «Математическая теория борьбы за существование» с послесловием Ю.М. Свирежева, в котором рассматривается история развития математической экологии в период 1931‑1976 гг. Книга Вольтерра написана так, как пишут книги по математике. В ней сначала сформулированы некоторые предположения о математических объектах, которые предполагается изучать, а затем проводится математическое исследование свойств этих объектов. Системы, изученные Вольтерра, состоят их двух или нескольких видов. В отдельных случаях рассматривается запас используемой пищи. В основу уравнений, описывающих взаимодействие этих видов, положены следующие представления. 4.1 Гипотезы Вольтерра 1. Пища либо имеется в неограниченном количестве, либо ее поступление с течением времени жестко регламентировано. 2. Особи каждого вида отмирают так, что в единицу времени погибает постоянная доля существующих особей. 3. Хищные виды поедают жертв, причем в единицу времени количество съеденных жертв всегда пропорционально вероятности встречи особей этих двух видов, т.е. произведению количества хищников на количество жертв. 4. Если имеется пища в ограниченном количестве и несколько видов, которые способны ее потреблять, то доля пищи, потребляемой видом в единицу времени, пропорциональна количеству особей этого вида, взятому с некоторым коэффициентом, зависящим от вида (модели межвидовой конкуренции). 5. Если вид питается пищей, имеющейся в неограниченном количестве, прирост численности вида в единицу времени пропорционален численности вида. 6. Если вид питается пищей, имеющейся в ограниченном количестве, то его размножение регулируется скоростью потребления пищи, т.е. за единицу времени прирост пропорционален количеству съеденной пищи. 4.2 Аналогии с химической кинетикой Эти гипотезы имеют близкие параллели с химической кинетикой. В уравнениях популяционной динамики, как и в уравнениях химической кинетики, используется “принцип соударений”, когда скорость реакции пропорциональна произведению концентраций реагирующих компонентов. 4.3 Вольтерровские модели взаимодействий Действительно, согласно гипотезам Вольтерра, скорость процесса отмирания каждого вида пропорциональна численности вида. В химической кинетике это соответствует мономолекулярной реакции распада некоторого вещества, а в математической модели – отрицательным линейным членам в правых частях уравнений. Согласно представлениям химической кинетики, скорость бимолекулярной реакции взаимодействия двух веществ пропорциональна вероятности столкновения этих веществ, т.е. произведению их концентрации. Точно так же, в соответствии с гипотезами Вольтерра, скорость размножения хищников (гибели жертв) пропорциональна вероятности встреч особей хищника и жертвы, т.е. произведению их численностей. И в том и в другом случае в модельной системе появляются билинейные члены в правых частях соответствующих уравнений. Наконец, линейные положительные члены в правых частях уравнений Вольтерра, отвечающие росту популяций в неограниченных условиях, соответствуют автокаталитическим членам химических реакций. Такое сходство уравнений в химических и экологических моделях позволяет применить для математического моделирования кинетики популяций те же методы исследований, что и для систем химических реакций. 4.4 Классификация типов взаимодействий В соответствии с гипотезами Вольтерра взаимодействие двух видов, численности которых x 1 иx 2 , могут быть описаны уравнениями: (9.1) Здесь параметры a i ‑ константы собственной скорости роста видов, c i ‑ константы самоограничения численности (внутривидовой конкуренции), b ij ‑ константы взаимодействия видов, (i , j= 1,2). Знаки этих коэффициентов определяют тип взаимодействия. В биологической литературе обычно классифицируют взаимодействия по участвующим в них механизмам. Разнообразие здесь огромно: различные трофические взаимодействия, химические взаимодействия, существующие между бактериями и планктонными водорослями, взаимодействия грибов с другими организмами, сукцессии растительных организмов, связанные в частности, с конкуренцией за солнечный свет и с эволюцией почв и т.д. Такая классификация кажется необозримой. E . Одум, учитывая предложенные В.Вольтерра модели, предложил классификацию не по механизмам, а по результатам. Согласно этой классификации, оценивать взаимоотношения следует как положительные, отрицательные или нейтральные в зависимости от того, возрастает, убывает или остается неизменной численность одного вида в присутствии другого вида. Тогда основные типы взаимодействий могут быть представлены в виде таблицы. ТИПЫ ВЗАИМОДЕЙСТВИЯ ВИДОВ
В последнем столбце указаны знаки коэффициентов взаимодействия из системы (9.1) Рассмотрим основные типы взаимодействий УравненияКОНКУРЕНЦИИ: Как мы уже видели в лекции 6, уравнения конкуренции имеют вид: 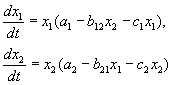 (9.2) (9.2)Стационарные решения системы: Начало координат, при любых параметрах системы представляет собой неустойчивый узел. C тационарное состояние представляет собой седло при a 1 >b 12 /с 2 и устойчивый узел приa 1 <12 /с 2 . Это условие означает, что вид вымирает, если его собственная скорость роста меньше некоторой критической величины. C тационарное решение ¾ седло при a 2 >b 21 /c 1 и устойчивый узел при a 2< b 21 /c 1 Стационарное состояние характеризует сосуществование двух конкурирующих видов и представляет собой устойчивый узел в случае выполнения соотношения: Отсюда следует неравенство: b 12 b 21 <=>1 c 2 , позволяющее сформулировать условие сосуществования видов: Произведение коэффициентов межпопуляционного взаимодействия меньше произведения коэффициентов внутри популяционного взаимодействия. Действительно, пусть естественные скорости роста двух рассматриваемых видов a 1 , a 2 одинаковы. Тогда необходимым для устойчивости условием будет c 2 > b 12 ,c 1 > b 21 . Эти неравенства показывают, что увеличение численности одного из конкурентов сильнее подавляет его собственный рост, чем рост другого конкурента. Если численность обоих видов ограничивается, частично или полностью, различными ресурсами, приведенные выше неравенства справедливы. Если же оба вида имеют совершенно одинаковые потребности, то один из них окажется более жизнеспособным и вытеснит своего конкурента. Поведение фазовых траекторий системы дает наглядное представление о возможных исходах конкуренции. Приравняем нулю правые части уравнений системы (9.2): x 1 (a 1 –c 1 x 1 – b 12 x 2) = 0 (dx 1 /dt = 0), x 2 (a 2 –b 21 x 1 – c 2 x 2) = 0 (dx 2 /dt = 0), При этом получим уравнения для главных изоклин системы x 2 = – b 21 x 1 / c 2 +a 2 /c 2 , x 2 = 0 – уравнения изоклин вертикальных касательных. x 2 = – c 1 x 1 / b 12 +a 1 /b 12 , x 1 = 0 – уравнения изоклин вертикальных касательных. Точки попарного пересечения изоклин вертикальных и горизонтальных касательных систем представляют собой стационарные решения системы уравнений (9.2.), а их координаты Возможное расположение главных изоклин в системе (9.2) изображено на рис.9.1. Рис. 9.1 а соответствует выживанию вида x 1 , рис. 9.1 б – выживанию вида x 2 , рис. 9.1 в – сосуществованию видов при выполнении условия (9.6). Рисунок 9.1 г демонстрирует триггерную систему. Здесь исход конкуренции зависит от начальных условий. Ненулевое для обоих видов стационарное состояние (9.5) – неустойчивое. Это – седло, через которое проходит сепаратриса, отделяющая области выживания каждого из видов. 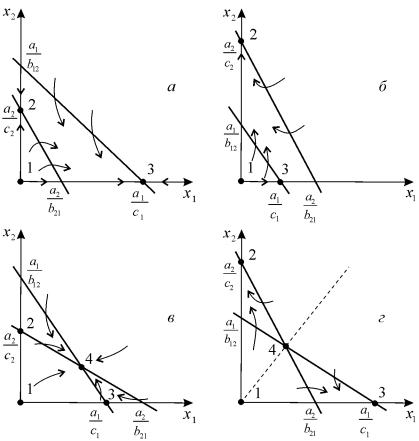 Рис. 9.1. Расположение главных изоклин на фазовом портрете вольтерровской системы конкуренции двух видов (9.2) при разном соотношении параметров. Пояснения в тексте. Для изучения конкуренции видов ставились эксперименты на самых различных организмах. Обычно выбирают два близкородственных вида и выращивают их вместе и по отдельности в строго контролируемых условиях. Через определенные промежутки времени проводят полный или выборочный учет численности популяции. Регистрируют данные по нескольким повторным экспериментам и анализируют. Исследования проводили на простейших (в частности, инфузориях), многих видах жуков рода Tribolium, дрозофиллах, пресноводных ракообразных (дафниях). Много экспериментов проводилось на микробных популяциях (см. лекция 11). В природе также проводили эксперименты, в том числена планариях (Рейнольдс), двух видах муравьев (Понтин) и др. На рис. 9.2. изображены кривые роста диатомовых водорослей, использующих один и тот же ресурс (занимающих одну и ту же экологическую нишу). При выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддержвает концентрацию ресурса (силиката) на постоянно низком уровне. Б. При выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. В. При совместном культивировании (в двух повторностях) Synedrauina вытесняет Asterionella Formosa . По-видимому, Synedra 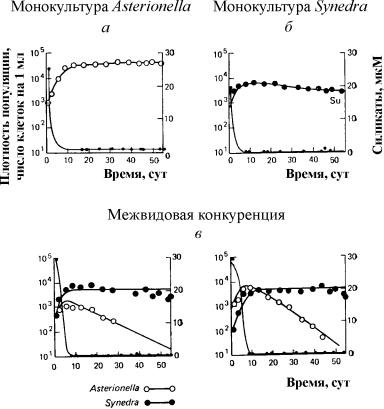 Рис. 9.2. Конкуренция у диатомовых водорослей. а ‑ при выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддерживает концентрацию ресурса (силиката) на постоянно низком уровне.б ‑ при выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. в ‑ при совместном культивировании (в двух повторностях) Synedruina вытесняет Asterionella Formosa . По-видимому, Synedra выигрывает конкуренцию благодаря своей способности к более полному использованию субстрата (см. также Лекцию 11). Широко известны эксперименты по изучению конкуренции Г. Гаузе, продемонстрировавшие выживание одного из конкурирующих видов и позволившие ему сформулировать «закон конкурентного исключения». Закон гласит, что в одной экологической нише может существовать только один вид. На рис. 9.3. приведены результаты экспериментов Гаузе для двух видов Parametium , занимающих одну экологическую нишу (рис. 9.3 а, б) и видами, занимающими разные экологические ниши (рис. 9.3. в). 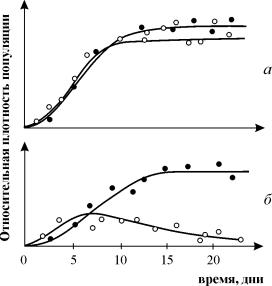 Рис. 9.3. а - Кривые роста популяций двух видов Parametium в одновидовыхкультурах. Черные кружки – P Aurelia , белые кружки – P . Caudatum б - Кривые роста P Aurelia и P . Caudatum в смешанной культуре. По Gause , 1934 Модель конкуренции (9.2) имеет недостатки, в частности, из нее следует, что сосуществование двух видов возможно лишь в случае, если их численность ограничивается разными факторами, но модель не дает указаний, насколько велики должны быть различия для обеспечения длительного сосуществования. В то же время известно, что для длительного сосуществования в изменчивой среде необходимо различие, достигающее определенной величины. Внесение в модель стохастических элементов (например, введение функции использования ресурса) позволяет количественно исследовать эти вопросы. |
