Курсовая ТЭЦ. Пример выполнения курсовой работы ТЭЦ. Исследование линейных электрических цепей наименование темы пояснительная записка

• Название: Исследование линейных электрических цепей наименование темы пояснительная записка
• Анкор: Курсовая ТЭЦ
• Дата: 03.12.2022
• Размер: 449.18 Kb.
• Имя файла: Пример выполнения курсовой работы ТЭЦ.docx
• Тип: Исследование; #825828
• страница: 10 из 22

Расчет электрических цепей при гармоническом воздействии

1. Теоретическая часть

Переменным током называется такой ток, который изменяется во времени по величине и направлению.

Электрический сигнал – это электрическое напряжение или ток, изменяющиеся с течением времени и несущие в себе информацию

Сигналы подразделяются на периодические и непериодические. У периодических сигналов форма сигнала повторяется через определенный промежуток времени, у непериодических эта особенности отсутствует.

Периодические сигналы принято подразделять на гармонические и импульсные. Гармонические – это сигналы, изменяющиеся по закону синусов. Импульсные сигналы – это колебания, присутствующие лишь в пределах конечного отрезка времени.

1. Основные параметры синусоидального тока

Синусоидальный ток является периодическим. Пусть ток изменяется по закону синусов i  I_m sint  . График этой функции показан на рисунке 6.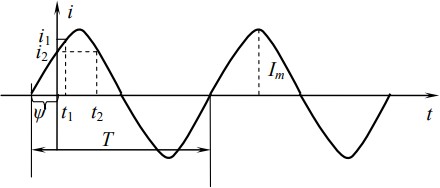



Рисунок 6
Мгновенное значение – это значение тока в данный момент времени. Мгновенное значение меняется от точки к точке и обозначается строчной буквой i.

Амплитуда – наибольшее значение синусоидального тока. Амплитуда тока обозначается прописной буквой с индексом – I_m. Аналогично обозначаются амплитуды напряжений – U_m и ЭДС – E_m.

Периодом Т называется наименьший промежуток времени, за который мгновенное значение тока, пройдя полный цикл, достигает первоначального значения. Период измеряется в секундах [c].

Частота переменного тока (циклическая) – величина, обратная периоду Фаза или фазовый угол – это угловое значение аргумента синусоидальной

функции t  .

Начальная фаза – значение фазы синусоидального тока в начальный момент времени t = 0: t    .

Угловая частота  – скорость изменения фазового угла. За время, равное периоду, фазовый угол равномерно изменяется на 2π. Поэтому угловую частоту можно определить, как

_{𝜔 =} 2𝜋

𝑇
Единицей измерения угловой частоты является рад/с.

(15)

Действующее значение переменного тока численно равно такому постоянному току, который в элементе цепи за время, равное периоду Т, выделяет такое же количество тепла, какое в том же элементе за то же время при тех же условиях выделяет переменный ток.

Действующее значение синусоидального тока в 2 раз меньше его амплитудного значения. То же самое можно сказать о напряжении и ЭДС.

Действующие значения токов, напряжений и ЭДС обозначаются прописной буквой без индекса. Все расчеты в цепях переменного тока выполняются для действующих значений токов, напряжений и ЭДС.
Комплексное число можно представить в трех формах записи.

1. 
   Алгебраическая форма позволяет выразить комплексное число через координаты точки.
   

А^̇ = 𝑎 + 𝑗𝑏 (16)

2. 
   Тригонометрическая форма. Из треугольника 0Аа видно, что a 
   

Acos , а b  Asin , тогда комплексное число можно записать в виде

А^̇ = 𝐴 𝑐𝑜𝑠  + 𝑗 𝐴𝑠𝑖𝑛  (17)

3. 
   Показательная форма. Воспользуемся формулой Эйлера, связывающей тригонометрические функции с показательными:
   

𝑒^±𝑗 = 𝑐𝑜𝑠  + 𝑗 𝑠𝑖𝑛  (18)

тогда комплексное число можно записать в виде
А^̇ = 𝐴𝑒^𝑗, (19)

Где А – модуль комплексного числа, который характеризует длину вектора;

ψ – аргумент комплексного числа, который характеризует угол поворота вектора относительно действительной оси.

Комплексные числа можно складывать, вычитать, делить и умножать. Как правило, сложение и вычитание производятся в алгебраической форме, а

умножение и деление в показательной. Переход от одной формы к другой осуществляется по следующим правилам.

Если известны координаты точки А^̇ , то модуль комплексного числа А можно найти по теореме Пифагора:

𝐴 = √𝑎² + 𝑏² (20)

Аргумент:
ψ = arctg ^b

a

(21)

Переход от показательной формы к алгебраической осуществляется через тригонометрическую форму, то есть выражаем экспоненту по формуле Эйлера и находим a  Acos , b  Asin.

При расчете комплексных чисел следует помнить следующие правила:

j^π −j^{π 1}

j = e ² ; −j = e ² ; _j = −j.

Две комплексные величины, имеющие равные модули и одинаковые по величине, но противоположные по знаку аргументы, называются комплексно- сопряженными.